0

Trigonometrik Fonksiyonlar

Tim Brzezinski, Mustafa Eroğlu, Mar 9, 2023

Radyanla Çalışmak

1. Radyan Nedir ?
2. Radyan Ölçüsü Verilen Açıların Oluşturulması
3. 1 Radyan : Tanım
4. Animasyon 69
5. Radyan Çizer
6. Video: Radyan - Devir
7. Quiz: Standart Konumda Açı Çizimi
8. DERECE'den RADYAN'a ve RADYAN'dan DERECE'ye geçiş
9. DERECE den RADYAN a ve RADYAN dan DERECE ye :

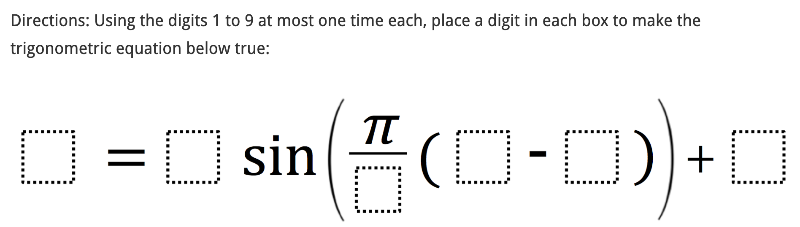
Radyan Nedir ?

Bu uygulama ile birkaç dakika etkileşime geçin .Sonra aşağıdaki soruları cevaplayın.

Radyan ,bir açı ölçü birimidir (derece gibi). yalnızca yukarıda gördüklerinize dayanarak (ve Google'ı [b] kullanmadan ) bir açının bir radyanı ölçmesinin ne anlama geldiğini kendi kelimelerinizle açıklayınız .[/b]

Çemberin 360 dereceyi ölçen tam bir yay olduğunu biliyoruz . Gördüklerinize göre , tam bir daire (devir) oluşturan yaklaşık radyan değerini hesaplayınız.

1.2.

1.3.

1.4.

1.5.

1.6.

1.7.

1.8.

1.9.

2.

Standart Konumdaki Açılar , Koterminal Açılar ,Trigonometrik Oranlar

1. Standart Konumdaki Açılar
2. Animasyon 176
3. Açı Oryantasyonları ( Standart Konum )
4. Animasyon 180
5. Animasyon 181
6. Esas Ölçülü Açı Eylemi!!!
7. Animasyon 183
8. Quiz: Çizim Açıları Standart Konumda
9. Esas Ölçülü Açılar : Soru Oluşturucu
10. Tanım: Trigonometrik Oranlar
11. Birim Çember ve Sinüs Grafiği
12. Birim Çember ve Tanjant Grafiği
13. Birim Çember ve Kosinüs Grafiği

2.1.

Standart Konumdaki Açılar

Aşağıdaki koordinat düzleminde çizilen açı , STANDART KONUM da çizilmiş olarak sınıflandırılır.Uygulamayla bir dakika etkileşim kurun .[br]Ardından aşağıdaki soruyu cevaplayın.

STANDART KONUMDAKİ AÇI:

1.

Koordinat düzleminde [b] çizilen bir açının STANDART KONUMDA çizilmesi ne anlama gelir?[br][br][/b](Tanımınız 2 kriter listelemelidir.)

2.2.

2.3.

2.4.

2.5.

2.6.

2.7.

2.8.

2.9.

2.10.

2.11.

2.12.

2.13.

3.

Özel Açıların Trigonometrik Fonksiyonları

3.1.

Dik Üçgen Oluşturucu

Matematik öğretmenleri ve öğrenciler:

Burada , yalnızca 2 nokta çizerek ve SONRA dar iç açılarından birinin ölçüsünü girerek hızlı bir şekilde bir dik üçgen oluşturmanıza olanak tanıyan özel bir aracımız (en sağda) var.[br][br][b]Not: [/b][br]Dik üçgen aracını seçerek ( en sağda) 2 nokta çizin. Ardından , herhangi bir dar açının ölçüsünü girin . (Ayrıca dilerseniz [math]\alpha[/math] = sürgünün adını da girebilirsiniz ) bu dar açının ölçüsünü hızlı bir şekilde değiştirmek isterseniz açıya sürgünün adını da girebilirsiniz.

Quick (Silent) Demo: How to Use

3.2.

3.3.

3.4.

3.5.

3.6.

3.7.

3.8.

3.9.

3.10.

3.11.

3.12.

3.13.

3.14.

3.15.

3.16.

3.17.

3.18.

3.19.

3.20.

3.21.

3.22.

3.23.

3.24.

3.25.

3.26.

3.27.

3.28.

3.29.

3.30.

3.31.

3.32.

3.33.

3.34.

3.35.

3.36.

3.37.

3.38.

3.39.

3.40.

3.41.

4.

Even and Odd Functions

1. Sine and Cosecant Functions (Special Property)
2. Sine Identity
3. Animation 150
4. Cosine and Secant Functions (Special Property)
5. Cosine Identity
6. Animation 149
7. Tangent and Cotangent Functions (Special Property)'in kopyası
8. Animation 145
9. Tangent Identity
10. Animation 151

4.1.

Sine and Cosecant Functions (Special Property)

Suppose [math]\theta[/math] is an angle drawn in standard position. [color=#666666][b]Let [i]P[/i]([i]x[/i], [i]y[/i]) be any point in the coordinate plane[/b][/color] and let[color=#666666][b] [i]r[/i] = the distance from [i]P[/i] to the origin[/b][/color]. [br][br]Recall [math]sin\left(\theta\right)=\frac{y}{r}[/math] and [math]csc\left(\theta\right)=\frac{r}{y}[/math]. [br][br]Interact with the applet below for a minute or two. Then answer the questions that follow. [br][color=#666666][b](Be sure to move point [i]P[/i] to various locations!) [/b][/color][br][br]

1.

Regardless of where [i][color=#666666][b]P[/b][/color][/i] lies, what is the relationship between the values of the ratios [math]sin\left(-\theta\right)[/math] and [math]sin\left(\theta\right)[/math]?

2.

Regardless of where [i][color=#666666][b]P[/b][/color][/i] lies, what is the relationship between the values of the ratios [math]csc\left(-\theta\right)[/math] and [math]csc\left(\theta\right)[/math]?

3.

What do these 2 observations imply about the sine and cosecant functions? (Click [url=https://www.geogebra.org/m/pb8Drtd5]here[/url] and/or [url=https://www.geogebra.org/m/GY9tNvfB]here[/url] for a hint!)

4.2.

4.3.

4.4.

4.5.

4.6.

4.7.

4.8.

4.9.

4.10.

5.

Graphing and Writing Trig Functions

1. Sine Spaghetti (by Steve Phelps)
2. Cosine Spaghetti
3. Sine and Cosine Graphing Template
4. Sine and Cosine π-friendly Graphing Template
5. Sine Function Anatomy and Exploration
6. Unit Circle to Sine and Cosine Functions
7. Sine & Cosine Period Action (1)!
8. Animation 190
9. Animation 191
10. Sine & Cosine Period Action (2)!
11. Tangent Function Exploration
12. Tangent Period Action (1)!
13. Tangent Period Action (2)!
14. Animation 192
15. Cotangent Function Exploration'in kopyası
16. Transforming Sine and Cosine Functions (1): Dynamic Illustrator'in kopyası
17. Transforming Sine and Cosine Functions (2): Dynamic Illustrator
18. Transforming the Sine Function (All Transformations)
19. Graphing Sine & Cosine Functions (II)
20. Graphing Sine & Cosine Functions (I)
21. Transformations of a Sinusoid
22. Basic Trig Graphing Open Middle Problem
23. Quiz: Graphing Sine & Cosine Functions (Amplitude & Vertical Shift Only)
24. Writing Sine and Cosine Functions (with Amplitude & Vertical Shift Changes)
25. Open Middle: Graphing Trig Functions Exercise
26. Open Middle: Graphing Trig Functions Exercise (2)
27. Modeling with Trigonometric Functions
28. Ferris Wheel Action!!!

5.1.

Sine Spaghetti (by Steve Phelps)

Original creativity and design in the app below by [url=https://www.geogebra.org/u/stevephelps]Steve Phelps[/url].

Move the [b]LARGE POINT [i]P[/i] [/b]to various locations around the circle. Each time you do, [br][list=1][*]Press the [b][color=#cc0000]Make Segment[/color][/b] button. [/*][*]Drag the segment you just made so its endpoint that originally touched the horizontal axis now touches the open-holed point on the right. (See quick screencast below.) [/*][*]Repeat steps (1) - (2) numerous times. Get as many segments dragged to the right as you can. [/*][*]Use the [b]PEN tool[/b] to draw a curve that connects the other endpoints of the segments that do not touch the horizontal axis. [/*][/list]

What does this curve look like to you? Describe.

5.2.

5.3.

5.4.

5.5.

5.6.

5.7.

5.8.

5.9.

5.10.

5.11.

5.12.

5.13.

5.14.

5.15.

5.16.

5.17.

5.18.

5.19.

5.20.

5.21.

5.22.

5.23.

5.24.

5.25.

5.26.

5.27.

5.28.

6.

Solving Trig Equations and Modeling

1. Open Middle: Trigonometric Equation (1)
2. Open Middle: Trigonometric Equation (2)
3. Open Middle: Creating Trig EQ's Exercise Set'in kopyası
4. Ferris Wheel (1): Modeling with Trigonometric Functions
5. Ferris Wheel (2): Modeling with Trigonometric Functions
6. Interesting Triangles Phenomenon

6.1.

Open Middle: Trigonometric Equation (1)

Creation of this resource was inspired by this original Open Middle exercise created by Kevin Rees:

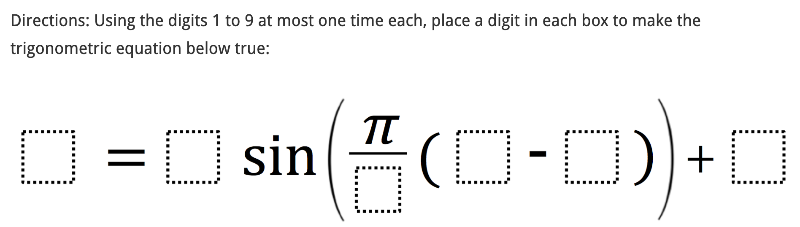
Directions: Using digits 1-9 AT MOST ONE TIME EACH, type a digit in each box to make the trigonometric equation below true. Build and modify as much as you need.

Directions: Using digits 1-9 AT MOST ONE TIME EACH, create another valid setup that is ENTIRELY DIFFERENT from the one you created above.

Directions: Using digits 1-9 AT MOST ONE TIME EACH, create another valid setup that is ENTIRELY DIFFERENT from the two setups you created above.

What is the LOWEST POSSIBLE OUTPUT (value that both sides equal) you can create given the constraints of this problem? Create a setup that shows this below.

What is the HIGHEST POSSIBLE OUTPUT (value that both sides equal) you can create given the constraints of this problem? Create a setup that shows this below.

6.2.

6.3.

6.4.

6.5.

6.6.

7.

Proving Trig Identities

1. New Trig IDs From Similar Right Triangles
2. New Trig ID's from Similar Right Triangles (V2)
3. Pythagorean Trigonometric Identity (1)
4. Trig Identity via Areas: Dynamic Illustrator
5. Trig Identity via Areas (2): Dynamic Illustrator
6. Trig ID Movie (II)
7. Trig ID Movie (III)

7.1.

New Trig IDs From Similar Right Triangles

Recall the definitions of the 6 trigonometric functions defined at an angle drawn in standard position within the coordinate plane. (These ratios were defined in terms of [i]x[/i], [i]y, [/i]& [i]r[/i]). [br][br]Interact with this diagram for a minute or two. (The 2 LARGE POINTS are moveable). [br]Then, answer the question prompts that follow.

1.

Explain why each segment IS what it is. (Some are much easier than others). [br][br]For example, how do we know the [b][color=#9900ff]purple segment has a length = to the tangent of[/color][/b] [math]\theta[/math]?

2.

How many pairs of similar triangles do you see here? How do we know these triangles you reference are all similar to each other?

3.

You have previously learned that similar triangles have corresponding sides that are in proportion. That is, ratios of corresponding sides of similar triangles are all equal in value. [br][br][i]Given this fact, try to author other trig identities from this picture.[/i] You can type them in the space below. Or, even better, feel free to type or use the digital pen to write them in the app below this space. [br]

Write some new trig identities here!

Write some new trig identities here! Use this space if you run out of room above.

7.2.

7.3.

7.4.

7.5.

7.6.

7.7.

8.

Inverse Trig Functions

1. Using Inverse Trig Functions to Express Angle Measures
2. Creating Inverse Sine and Inverse Cosine Functions
3. Evaluating Inverse Trig Functions of Special Ratios
4. Compositions of Trig & Inverse Trig Functions (1)
5. Evaluating Compositions of Trig & Inverse Trig Functions (2)
6. Inverse Relations: Graphs
7. Sine Function Domain Restriction Options?
8. Cosine Function Domain Restriction Options?
9. Tangent Function Domain Restriction Options?
10. Inverse Trig Functions: Intuitive Explorations

8.1.

Using Inverse Trig Functions to Express Angle Measures

Use inverse trigonometric functions to enter 3 different exact values for the measure of angle A. Do the same for angle B. Then, approximate angle A's measure to the nearest tenth (at bottom).

Quick silent demo

8.2.

8.3.

8.4.

8.5.

8.6.

8.7.

8.8.

8.9.

8.10.

9.

Proving Advanced Trig Identities

1. Law of Sines: Intro via Areas
2. Open Middle: Ambiguous Case Setups
3. Exploring Sines: Another Key Triangle Relationship
4. Sine & Cosine of a Sum: Discovery
5. Trig ID: Geometric Investigation
6. Trig Identity (4) - Geometric Investigation
7. Tangent of a Sum: Discovery
8. Tangent of a Difference: Trig Identity Puzzle + Proof!
9. Cotangent of a Sum: Discovery
10. Bizzare Trig Identity?
11. Animation 105
12. sin(75) & cos(75) activity

9.1.

Law of Sines: Intro via Areas

In the app below, points A and B are MOVEABLE. You can change the sizes of the colored angles using the two colored sliders in the lower left corner. Slide the long slider slowly and carefully watch what happens!

[img width=329,height=170]https://lh6.googleusercontent.com/MP__fZu80x1doBPReABsDuZddxJj0leoUvgMv70UrxfEpTMWH9GP7HKvIVpedWo1Fyc3Ww1ZrdCLY_l4LOa_nxirCJsGmRChdt3jwP0dIWAhks2_yvuMJNsWCI-bWRyHQi1iLETo[/img][br][br][br][br]What is the area of this rectangle in terms of [i][b]a[/b][/i] and [i][b]sin B[/b][/i]?

[img width=236,height=220]https://lh5.googleusercontent.com/bGoknLi6GkA-yFtCKiWWaplR8IH6-_ixHn8_hZ6X8wFAnQb1m50pMbqd-fa6EEGAFPSYF3nJAM4DJQSNbGAQRO9HBqLUqf1ac0iWUhGBTpw9ZAkDUjXUlOVK35Uu7hCjGozYBNK6[/img][br][br][br][br][br][br][br]What is the area of this rectangle in terms of[b] [i]b[/i] [/b]and [b][i]sin[/i] [i]A[/i][/b]?

What can we conclude about the areas of these two rectangles? Why can we conclude this?

Given your responses to the questions above, write an equation that expresses the relationship among [b][i]a[/i], [i]b[/i], sin [i]A[/i], and sin [i]B[/i]. [/b]

Copy the equation you wrote above in the app below. Then rewrite an equivalent equation so that a and sin(A) appear on one side of the equation and so b and sin(B) appear on the other side.

Quick (silent) demo

9.2.

9.3.

9.4.

9.5.

9.6.

9.7.

9.8.

9.9.

9.10.

9.11.

9.12.

10.

Other Functions Resources

1. Functions Resources

10.1.

Functions Resources

[list][*][b][url=https://www.geogebra.org/m/k6Dvu9f3]Interpreting Functions[/url][/b][/*][*][b][url=https://www.geogebra.org/m/uTddJKRC]Building Functions[/url][/b][/*][*][b][url=https://www.geogebra.org/m/GMvvpwrm]Linear, Quadratic, and Exponential Functions[/url][/b][/*][*][b][url=https://www.geogebra.org/m/aWuJMDas]Trigonometric Functions[/url][/b][/*][/list]

Half-life function: Quick Exploration. (Large point & slider moveable.)

What does it mean for a function to be odd? (Points moveable.)

0