Extremums Using Derivatives: The Candidates Test
[size=200][size=150][center][/center][/size][/size][center]You now know how to find the extrema of a function on an open interval using the [color=#1e84cc][b]First Derivative Test[/b][/color]. But what if the interval is [b]closed[/b]? This is another essential skill for calculus and will be helpful in future units as well (hint: integrals).[/center][br][b][color=#1e84cc]The Plan:[/color][/b][br][list][*]identify extremums of a function (ie. maximums, minimums) on a [b]closed[/b] interval by using the [color=#1e84cc][b]Candidates[/b][/color][color=#1e84cc][b] Test[/b][/color][/*][*]conclusion[/*][/list][br][center]Do you think you can do it? Let's get started![/center][center][/center]
[size=200][color=#1e84cc][b][center]The Candidates Test[/center][/b][/color][/size]
[center][i]The function [math]h\left(x\right)=x^4-4x^3+20[/math] is continuous and differentiable on the closed interval [math]-2\le x\le4[/math]. Without a calculator, find the absolute maximum and minimum, if any, of [math]h[/math] in the given interval.[/i][/center]
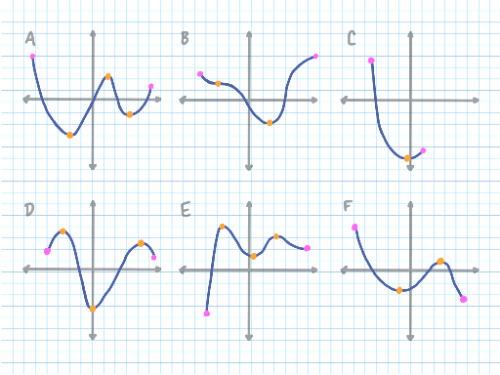
So, how do we go about this? Well, one thing to take note of is the [color=#1e84cc][b]Extreme Value Theorem[/b][/color] states "if [math]f[/math] is continuous on a closed interval [[math]a,b[/math]], then [math]f[/math] has both a maximum and a minimum value on the interval." From this definition, we know [math]h[/math] [i]must[/i] have an absolute minimum and maximum.[br][br]To find the absolute extrema, we need to use the [color=#1e84cc][b]Candidates Test[/b][/color]. For this test, we must evaluate the function at each [color=#1e84cc][b]critical point[/b][/color] and at each [color=#1e84cc][b]endpoint[/b][/color] of the interval because the maximum of the values will be the absolute maximum, and the minimum of these values will be the absolute minimum. But why the critical points [b]and[/b] the endpoints?[br][br]Look at these examples below:

Locate the absolute extremum of each graph. Notice how these values can lie on either the endpoints, critical points, or both of a function. Therefore, in a situation where you are without a graph and need to find the absolute extremum, it is unreliable to use only endpoints or only critical points to reach a conclusion when they can be anywhere. Because of this, we must test [b]both[/b] endpoints and critical points, regardless if one isn't an absolute extrema.
Now, back to the problem. We need to find where the endpoints of [math]h[/math] are. Remember, we are using the interval [math]-2\le x\le4[/math]. What are the x-values of these endpoints? Select all that apply.
So we have the x-values of the endpoints, but we also need the critical points. To find the x-values of the critical points, we must find the derivative of [math]h\left(x\right)=x^4-4x^3+20[/math]. What is the derivative of the fuction?
Now solve for the critical points, if any. Select all that apply.
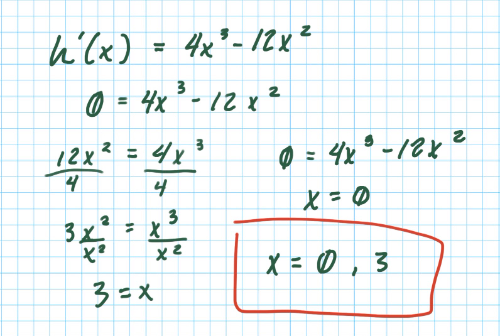
Great! We have all the x-values we need. For the next step, we need to evaluate the function at these special points. Create a table and solve for [math]h[/math] when x = -2, 0, 3, 4.
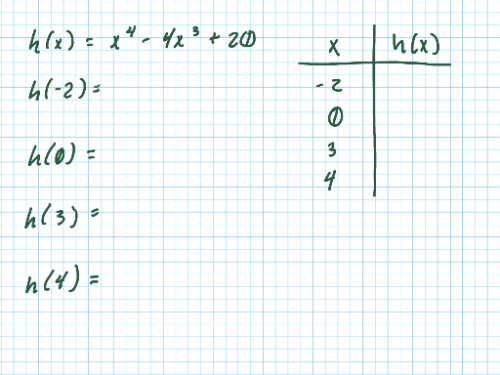
[math]h\left(-2\right)=[/math]?
[math]h\left(0\right)=[/math]?
[math]h\left(3\right)=[/math]?
[math]h\left(4\right)=[/math]?
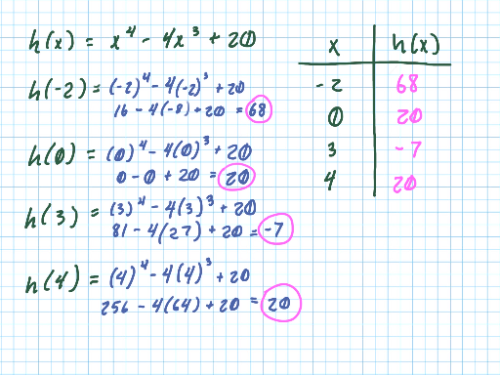
Now we have all of the information to determine the absolute extrema of [math]h[/math]. What is the absolute maximum and absolute minimum of [math]h[/math] on [math]-2\le x\le4[/math]? Justify your answer.
Let's check our work! Use the "Function Inspector" tool and click on the function. Make sure to scroll down to change the interval to [math]-2\le x\le4[/math]. What do you see?
[size=200][b][color=#1e84cc][center]Conclusion[/center][/color][/b][/size]Now you know how to do the [b][color=#1e84cc][size=100]Candidates Test[/size][/color][/b]. This is an extremely helpful skill in various calculus situations when you are looking for absolute extrema of a function without a calculator. If you know how to use the [color=#1e84cc][b]First Derivative Test[/b][/color] and the [color=#1e84cc][b]Candidates Test[/b][/color], you can do anything in the calculus world!