На предыдущем уроке вы вспоминали график квадратичной функции, заданной в виде [math]y=a\left(x-m\right)^2+n[/math]. [br]В следующем апплете потренируйтесь в изображении квадратичной функции, заданной в таком виде.
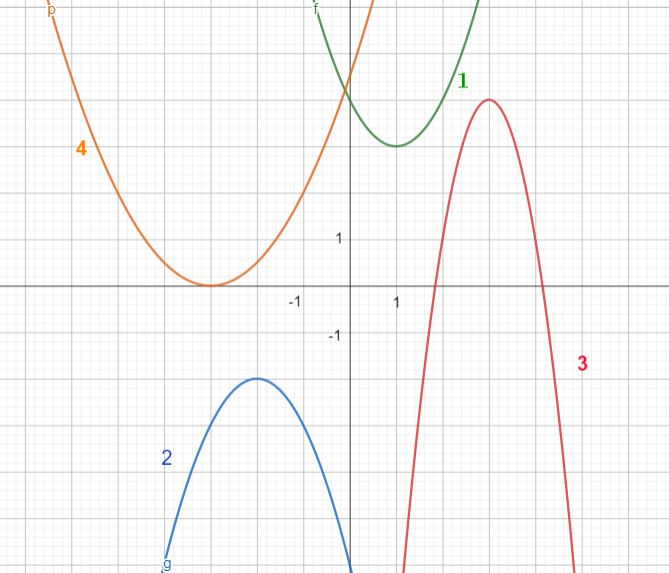
На рисунке изображены графики квадратичных фуекций.
Запишите графики функций , изображенных на рисунке выше.
В этой активности вы повторите свойства графика квадратичной функции , записанной в общем виде у= [math]ax^2+bx+c[/math].[br]
Q1: Какие изменения вы наблюдаете?
Q2. Когда a равно нулю, кривая представляет собой прямую линию. Почему?
Q3 Кривая проходит через фиксированную точку? Если да, то каковы координаты этой точки?
Q4: Чем больше значение «а» (когда а положительно), как это влияет на форму кривой?
1) Отметьте на оси Ох точку А и проведите через эту точку перпендикуляр к оси Ох.[br]2) Постройте серединный перпендикуляр к отрезку AF и найдите точку В его пересечение с перпендикуляром к оси Ох, проведенным через точку А. Включите у точки В опцию "оставлять след".[br]3) Двигая точку А, проследите за следом точки В.
Q1. Как называется полученная линия.
Q2. Подвигайте точку F и выясните, как связаны координаты точки F и координаты точки Н, которая является вершиной полученной линии.
Q3. Создайте ползунок (или ползунки) , и с их помощью найдите и запишите формулу соответствующей квадратичной функции. (F (0, 2))


