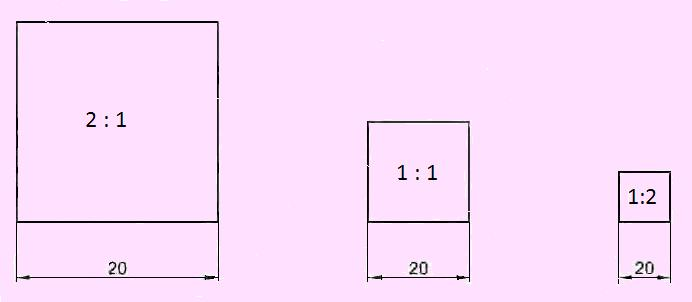
Razmera
Često je nemoguće predmet prikazati u svojoj realnoj veličini, pa ga je potrebno umanjiti, a nekada i uvećati. Razmera predstavlja odnos dimenzije predmeta na crtežu i u prirodi. [br]Ako se kaže da je u razmeri 1:100 to znači da će elementi na crtežu biti umanjeni 100 puta u odnosu na stvarne dimenzije. [br]Razmera 1:1 znači da su elementi na crtežu iste veličine kao u prirodi, i kaže se razmera u prirodnoj veličini. [br]Razmerom je određena veličina crteža, ali i svi ostali elementi kao i njihova jasnost i preglednost.[br][br]

Geografske karte prikazuju veće oblasti i na njima su uneti samo najvažniji objekti. Na njima su prikazane cele zemlje, kontinenti, pa i cela zemljina površina. Stoga se moraju izradjivati razmeri. Mora biti jasno definisano u kojim mernim jedinica je predstavljena karta, i koliko puta je umanjena.
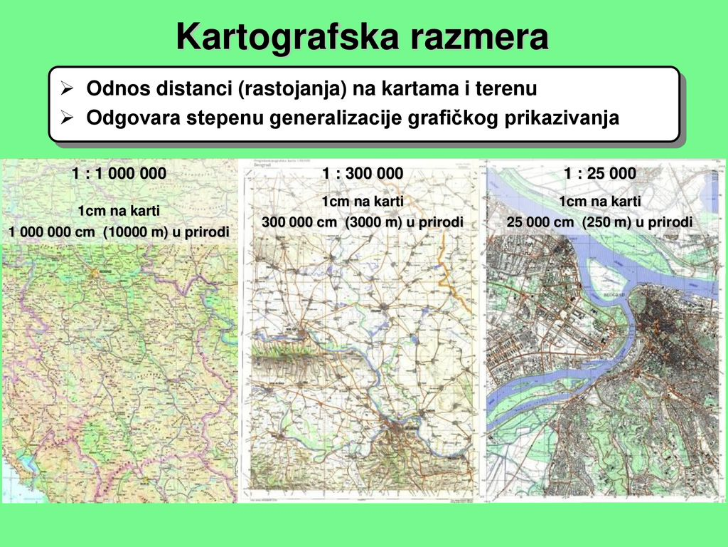
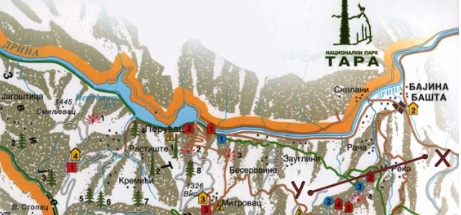
U matematici, pojam razmere je strogo definisan i odnosi se na sve veličine koje se mogu predstaviti svojim količnikom, a koje bi se prirodi mogle prikazati uzročno-posledičnom vezom. Po definiciji imamo:[br][i]Količnik realnih brojeva [math]a[/math] i [math]b[/math][math]\ne[/math][math]0[/math] tj. broj [math]\frac{a}{b}[/math]=[math]a\div b[/math] naziva se razmera brojeva [math]a[/math] i [math]b[/math][/i]. (Čita se [i]a [/i]prema [i]b.)[br][/i]Pr.1. Predstavi razmeru [math]315:105[/math] kao količnik dva uzajamno prosta broja.[br] [math]315:105=3:1[/math][justify]Pr.2. U kojoj razemeri je nacrtana geografska karta, ako je udaljenost između mesta X i Y na karti 4[i]cm[/i], a u prirodi 20[i]km?[/i][br][/justify]
Proporcija
[i]Ako dve razmere [math]a:b[/math] i [math]c:d[/math] imaju istu vrednost, onda se kaže da čine proporciju [math]a:b=c:d[/math]. [br]Važi za [math]b,d\ne0[/math], i ekvivalentno je sa [math]a\cdot d=b\cdot c[/math][/i][i].[br]Brojevi [math]a,b,c,d[/math] su članovi proporcije, delimo ih na unutrašnje [/i][math]b[/math][i],[math]c[/math] i spoljašnje članove [/i][math]a[/math][i],[math]d[/math]. [/i][br][br][br]
[b]Direktna i obrnuta proporcionalnost[/b][b][left][br][/left][/b]Veličine [i]x i y [/i]su:[b][br][/b][list][*] direktno proporcionalne ako je [math]y=kx[/math], gde je [math]k>0[/math].[/*][*]obrnuto proporcionalne ako je[math]y=\frac{k}{x}[/math], gde je [math]x\ne0[/math] i [math]k>0[/math].[/*][/list] npr.1 Odnos broja zaposlenih muškaraca i žena u nekoj firmi je direktno proporcionalan [br] odnosu ukupnog broja zaposlenih muškaraca i žena.[br] direktna proporcija ([u][i]više - više)[/i][/u] [br] [br]npr.2 Ako 4 radnika obave neki posao za 12 dana, koliko bi za taj isti posao trebalo dana da ga završi 6 radnika?[br][br] obrnuta (indirektna) proporcija ([u][i]više - manje)[/i][/u]