3.4 Exponential and Logarithmic Equations
Successful Criteria 1-Understand what does it mean to solve exponential equations 2-Solve exponential equations with same base and different base 3-Solve natural exponential equations. 4-Solve logarithmic equations 5-Solve natural logarithmic equations
Table of Contents
- Exponential Equations
- Solving Exponential Equations
- Practice Examples
- 3.4-Practice Problems-Classwork
- Exit ticket
- Exit ticket Exponential Equations
- Logarithmic Equations
- Solved Examples of Logarithmic equations
- Examples to try
- 3.4-Practice Problems-Classwork
- Drop Quiz
- Part A- Logarithmic equations
- Part B Exponential Equations
- Math game
- Math game-Exponential equations
- Practice with steps: Log Eqns LvL 2 (quotient)
- Extended topic
- Optional Advanced System of Equations involving Logarithms
Solving Exponential Equations
WHAT YOU ALREADY KNOW
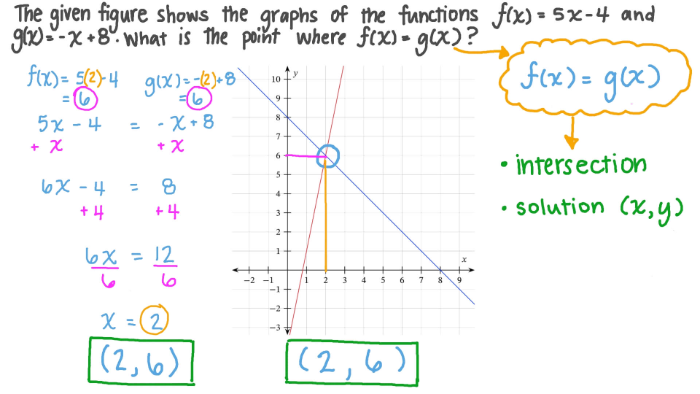
In Algebra 1 you have learned how to solve system of equations graphically.[br]In Algebra 2 you have learned that these equations can be of any form like quadratic functions. [br]In Pre Calculus the [b]ESSENTIAL QUESTION: How can you find the solution set of equations that involve exponential and logarithmic expressions?[/b][br]Below is an example to remind you what you used to do in Algebra 1 and 2.[br]
WHAT YOU WILL HAVE TO EXPLORE?
Given the two functions : [math]f\left(x\right)=2^{x-5}[/math]and [math]g\left(x\right)=2[/math]. [br]What is the solution set when f(x)= g(x) ?[br]Use the graph below to discover.[br]
Answer the following based on the graph above
The solution set of f(x) and g(x) is : [br]
Task 1: Exploring how to solve exponential equations with same base
Write down the steps for the solution below.
Are the steps above mathematically correct?
IDEA 2: Solving natural exponential equations with different base
[img]https://slideplayer.com/slide/8417517/26/images/3/Solving+exponential+equations+with+base+e.jpg[/img]
Try On your own:
Solve the following equation on your notebook [math]3e^{2x}-2=7[/math][br]Pick up the right answer from below
Choose the best answer
Exit ticket Exponential Equations
Instructions: Solve 2 examples
[b][u]Problem 1: [/u][/b][br]Step 1: Solve one exponential Equation with same base. [br]Step 2: Write the final answer in the box and check. once it shows correct in red, Take a screenshot and attach it on Canvas named: 3.4- Exit Ticket submission[br][b][u]Problem 2: [/u][/b][br]Step 1: Solve one exponential Equations with different base [br]Step 2: Write the final answer in the box and check. once it shows correct in red, Take a screenshot and attach it on Canvas named: 3.4- Exit Ticket submission[br]
Solved Examples of Logarithmic equations
2. Equations
A [b]logarithmic equation[/b] is an equation that has an unknown factor in the [b]argument of a logarithm[/b]. In reality, the resolution is reduced to the resolution of equations of the same type as the expressions in the arguments (quadratic equations, cubic equations, irrational equations...).
[b]Example 1[br][br][/b][b][img]https://www.matesfacil.com/ESO/logaritmos/elog1.png[/img][br][br][/b]We will use the properties of logarithms and that [math]log\left(1000\right)=log\left(10^3\right)=3.[/math][br][br][img]https://www.matesfacil.com/ESO/logaritmos/elog1-01.png[/img][br][br]We have an equality between logarithms, so the arguments (what is inside) has to be the same:[br][br][img]https://www.matesfacil.com/ESO/logaritmos/elog1-02.png[/img][br][br]The solution to the equation is [i]x = 50[/i].
[b]Example 2[br][br][/b][img]https://www.matesfacil.com/ESO/logaritmos/elog6.png[/img][br][br][img]https://www.matesfacil.com/ESO/logaritmos/elog6-1.png[/img]
Part A- Logarithmic equations
Instructions
[b][u]Problem1: [/u][/b][br]CLICK--> USING LOGARITHMS[br]Pick any equation. Solve on the A4 paper. You can use check box to check your answer.[br][u]Problem 2: [br][/u]CLICK -->USING EXPONENTIALS[br]Pick any equation. Solve on the A4 paper. You can use check box to check your answer.
Math game-Exponential equations
Optional Advanced System of Equations involving Logarithms
3. Logrithmic equation systems
[b]Example 1[br][/b] [br][img]https://www.matesfacil.com/ESO/logaritmos/slog1.png[/img][br][br]We apply the change of variable[br][br][img]https://www.matesfacil.com/ESO/logaritmos/slog1-01.png[/img][br][br]This way we obtain the following linear equation system[br][br][img]https://www.matesfacil.com/ESO/logaritmos/slog1-02.png[/img][br][br]we resolve it and we undo the cange of variable:[br][br][img]https://www.matesfacil.com/ESO/logaritmos/slog1-03.png[/img]
[b]Example 2[br][br][/b][b][img]https://www.matesfacil.com/ESO/logaritmos/slog9.png[/img][br][br][/b]First we apply the property [i]logarithm of a product[/i]:[br][br][img]https://www.matesfacil.com/ESO/logaritmos/slog9-01.png[/img][br][br]We apply the change of variable:[br][br][img]https://www.matesfacil.com/ESO/logaritmos/slog9-02.png[/img][br][br]and we obtain the following system:[br][br][img]https://www.matesfacil.com/ESO/logaritmos/slog9-03.png[/img][br][br]that has as solution:[br][br][img]https://www.matesfacil.com/ESO/logaritmos/slog9-04.png[/img][br][br]Finally, we undo the change of variable:[br][br][img]https://www.matesfacil.com/ESO/logaritmos/slog9-05.png[/img][br][br]We do not need to check the solutions.