Algebra
Table of Contents
- Part 1: Let's Talk About Ratios
- Let's Talk About Ratios
- Part 2: Dilations, Ratios and Proportions
- Copy of Dilations, Ratios, and Proportions
- Part 3: Ratios in a Cupcake Recipe
- Ratios in a Cupcake Recipe
- Part 4: Input Output Tables
- Input-Output
- Part 5: Measuring Angles
- Measuring Angles Using Protractor
- Part 6: Polynomials
- Polynomials
- Part 7: The Distributive Property
- The Distributive Property
- Part 8: Comparing Fractions
- Comparing Fractions
- Part 9: Perimeter and Area
- Perimeter and Area
- Part 10: Multiplication
- Multiplication Challenge
Let's Talk About Ratios
Marissa Hamilton[br]Standards: MAFS.6.RP.1.1[br][br][size=150][b]A ratio compares two quantities. [br][/b][/size]This can also be said as; a ratio compares two values[br][br]Later we will learn about the different formats of a ratio...yay![br][br]But first let's meet Sally!
[size=150][b][size=100]Sally decided to host a bake sale. She only offered chocolate chips cookies and sugar cookies at her bake sale. [br][br][/size][/b][b]The image below shows how many cookies were left over by lunch time. Use the image to follow along with the story and answer the questions. [br][br][/b][b]Let's call each chocolate chip cookie "c.c." and let's call each sugar cookie "sugar"[/b][/size]
[b]We see that there are 2 c.c. and 3 sugar, giving us a total of 5 cookies. Let's think about how we can use what we already know to form ratios. [/b]
First, let's compare the chocolate chip cookies to the sugar cookies. [br][br]There are a few ways that we could show the ratio of c.c. to sugar[br][br]EX. [br][br][math]\frac{2c.c.}{3sugar}[/math] OR 2:3 OR 2 to 3[br][br]In the above example, the ratios are simply comparing the number/quantity of chocolate chip cookies to the number/quantity of sugar cookies.
[size=150][b]Think of it this way:[br][br]"a" represents the first quantity, while "b" represents the second quantity[br][br]Knowing this, the ratio of [u]a to b[/u] can be written as:[br][br][/b][/size][size=150][math]\frac{a}{b}[/math][b] OR a:b OR a to b[/b][/size]
[size=200]NOW Let's Practice![/size]
Do you remember Sally? Well let's find the ratio of the number of chocolate cookies to the total number of cookies.[br][br]pick all that apply
[size=100][size=150]Great Job with that question, practice makes perfect!![br][br]--- [br][br][/size][/size][size=150][b][size=200]You would never believe this...[/size][/b][/size][size=100][size=150][br] [br][b]Sally's neighbor, Lisa, wanted to thank Sally for having the bake sale. Lisa brought over an assortment of desserts. Sally decided to combine her leftover cookies AND the desserts that Lisa brought over. The picture below shows all of the treats. Yummy![/b][/size][/size]
[b]In fraction form, what is the ratio of chocolate chip cookies to cupcakes?[br][br]Make sure to include the variable names (cc and ccake)[br]Simplify, if necessary[br]do not[/b] include spaces in your answer[br]use the forward slash "/" to separate the numerator and the denominator
[b]In a:b form, what is the ratio of chocolate chip cookies to total number of treats?[br][br]No need to include variable names[br]Simplify, if needed[br][br]do not include spaces in your answer[/b]
[size=200]Remember:[br]A ratio ----- two quantities. [br][br]A ratio can be written as:[br]--- OR [math]\frac{a}{b}[/math] OR a to b[br][br]...oops, it looks like I forgot to finish the definition of ratio AND missed one of the ratio formats.[br][br]With the last two question, help me fill in the blanks[br][br][/size]
[b][size=100][size=200][size=150]A ratio does what with two quantities?[/size][/size][/size][/b]
[b][size=150]What was the missing ratio format that I forgot? [br][br]do not use any spaces[/size][/b]
Copy of Dilations, Ratios, and Proportions
[size=200][b][color=#cc4125]Ratios[/color][/b][/size]
[size=150][b][color=#0000ff]There are four cupcakes for two boys. How many cupcakes does each boy get? Each boy gets two cupcakes. If we had 3 boys and 6 cupcakes, each boy would still get 2 cupcakes because all the ratios can be reduced to 2:1. All the ratios, 2:1, 4:2 and 6:3 are equal. [/color][/b][/size]
Cupcakes to boys
Ratios
[b][color=#ff0000][size=150]Let's say I hired you to pour a sidewalk from my doorway to my driveway. The directions on the bag of powder cement you bought says you will need to make a mixture of water, sand and cement powder. For every 2 bags of cement, you will need to add 4 bags of sand. [/size][/color][/b]
Cement to Sand
[b][color=#351c75][size=150]I could make a smaller batch of cement mixture by using one bucket of cement powder and two buckets of sand. [/size][/color][/b]
[size=200][b][color=#a61c00]Proportions[/color][/b][/size]
[size=150][b][color=#1155cc]A proportion is the number of parts to a whole. For example, in order to make one batch of cement mixture I need 2 buckets of cement powder and 4 buckets of sand. [br] one whole batch = 2:4[br]The powder and sand are the parts that make up the whole batch of cement mixture. [/color][/b][/size]
[size=200][b][color=#ff0000]To eat a healthy meal, follow the recommended proportions of food groups. [/color][/b][/size]
[b][size=200][color=#cc4125]Dilation[/color][/size][/b]
[size=150][b][color=#ff0000]Notice that when the scale factor is less than one (SF < 1), the image gets smaller. When the scale factor is greater than one (SF > 1), the image gets larger. When the scale factor is equal to 1 (SF = 1), the image is the same size. [/color][/b][/size]
[b][size=150][color=#0000ff]A dilation can result in a smaller image, or a larger image depending on the [/color][size=200][color=#ff0000]scale factor[/color][/size][/size][/b]
[size=200][color=#a61c00][b]Scale Factor[/b][/color][/size]
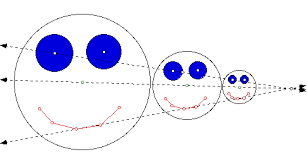
[b][size=200][color=#ff0000]A scale factor tells us how many times larger or smaller our image dilates. [/color][/size][/b]
Ratios in a Cupcake Recipe
Reason with equivalent ratios to adjust the recipe for cupcakes in this activity.
Input-Output
Complete tables of values that represent patterns of multiplication or division. Animate a function machine to represent patterns as algebraic expressions.
Measuring Angles Using Protractor
Measuring an Angle Using Protractor
Polynomials
A polynomial is a mathematical expression consisting of variables, coefficients, and non-negative integer exponents combined using addition, subtraction, and multiplication. It has a finite number of terms. For example, [code]x² - 4x + 7[/code] is a polynomial with one variable, and [code]x³ + 2xyz² - yz + 1[br][/code] is a polynomial with three variables. Polynomials are fundamental in mathematics and are used in various applications, including solving equations, defining functions, and approximating other functions.[br][br]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[br][b][br]Key Concepts:[/b][br][br][b]Terms:[/b] A polynomial is made up of terms, which are separated by addition or subtraction. Each term consists of a coefficient (a number) and a variable part (a variable raised to a non-negative integer power). [br][br][b]Variables:[/b] These are symbols, usually letters, that represent unknown or changing values.[br][br][b]Coefficients:[/b] These are the numerical factors that multiply the variables in each term. [br][br][b]Exponents:[/b] These are the powers to which the variables are raised. In polynomials, exponents must be non-negative integers (0, 1, 2, 3, ...). [br][br][b]Degree:[/b] The highest power of the variable in a polynomial is called its degree. [br] [br]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[br][b][br]Types of Polynomials:[br][br][/b][b]Monomial:[/b] A polynomial with only one term (e.g., 5x², -3y, 7). [br][br][b]Binomial:[/b] A polynomial with two terms (e.g., x + 2, 3y² - 4z). [br][br][b]Trinomial:[/b] A polynomial with three terms (e.g., x² + 2x + 1, 2p² - 7p + 3). [br][br][b]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[br][br]Polynomials can also be classified by their degree:[/b] [br][br][b]Zero Polynomial:[/b] Degree 0 (e.g., 5). [br][br][b]Constant Polynomial:[/b] Degree 0 (same as zero polynomial) (e.g., -2). [br][br][b]Linear Polynomial:[/b] Degree 1 (e.g., 2x + 1). [br][br][b]Quadratic Polynomial:[/b] Degree 2 (e.g., x² - 3x + 2). [br][br][b]Cubic Polynomial:[/b] Degree 3 (e.g., x³ + 2x² - x + 5). [br][br]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[br][br][b]Examples:[br][br][/b]3x + 2 is a linear binomial, 5x² - 2x + 1 is a quadratic trinomial, 7 is a constant monomial, and x³ - 8 is a cubic binomial. [br][br]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[br][b][br]Polynomials are used in various mathematical and scientific fields like:[br][br][/b]Polynomial equations (equations where one side is a polynomial) are used to model and solve problems in many areas. [br][br]Polynomial functions are used to represent relationships between variables and are fundamental in calculus and other areas of mathematics.[br][br]Polynomials can be used to approximate more complex functions that are difficult to work with directly. [br][br]These are advanced mathematical concepts used in algebra and algebraic geometry. [br][br]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The Distributive Property
The distributive property in math allows you to simplify expressions by distributing a factor to each term within parentheses. In simpler terms, it means you can multiply a number outside the parentheses by each number inside the parentheses and then add the results. [br][br]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[br][br][b]The Concept:[br][br][/b]When you have a number (or variable) multiplying a sum or difference within parentheses, the distributive property lets you "distribute" that number to each term inside the parentheses.[br][br]This means you multiply the number outside by each term inside separately, then add (or subtract) the results. [br][br]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[br][br][b]The Formula:[br][br][/b]The distributive property is often written as: a * (b + c) = (a * b) + (a * c) [br][br]It also applies to subtraction: a * (b - c) = (a * b) - (a * c) [br][br]Where 'a', 'b', and 'c' can be numbers or variables. [br][br]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[br][br][b]Example:[br][br][/b]Let's say you have the expression 3 * (4 + 2).[br][br]Using the distributive property:[br][br]3 * (4 + 2) = (3 * 4) + (3 * 2)[br][br]= 12 + 6[br][br]= 18[br][br]This is the same as first adding inside the parentheses (4 + 2 = 6) and then multiplying (3 * 6 = 18). [br][b][br][/b]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[br][br][b]Why is it useful?[br][br][/b]The distributive property helps simplify expressions, especially when terms inside parentheses cannot be combined (e.g., when they involve variables).[br][br]It's a fundamental concept used in algebra to solve equations and simplify expressions. [br][b][br][/b]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[b][br][/b]
Comparing Fractions
This activity was designed specially to address some students' question as to why they always had to compare, add or subtract two fractions by first making them equivalent fractions with common denominators.[br]Why not common numerators?[br]So here it is below. [br]Two fractions are visually represented as shaded portions of the circular pies divided into equal sized parts.[br][br]You can choose to have common denominators or numerators by clicking on the respective buttons.[br][br]The original question is: "Which fraction is larger? "[br]Then we should be asking :[br]How do we compare fractions by [br](a) making equivalent fractions with common denominators or by[br](b) having equivalent fractions with common numerators? or [br](c) simply see visually which of the two fractions of a circular pie is larger?[br][br]Some pairs of fractions to compare :[br]1/2 vs 1/3[br]1/3 vs 2/5[br]1/4 vs 2/9[br]2/5 vs 3/7[br]3/5 vs 5/9[br]5/8 vs 6/7
In conclusion, is it easier to add and subtract fractions with like denominators or fractions with unlike denominators?
Perimeter and Area
Do you have enough information to say how big the pool is?
Why not?
Use the DISTANCE OR LENGTH tool to measure the sides of the pool.
Imagine that one unit on the graph is one foot in real life.
How many feet long is the distance from C to F? Include units.
How many feet long is the distance from E to F? Include units.
The shape of the pool is a QUADRILATERAL specifically a RECTANGLE. The red rectangle below traces the edge of the pool.
Can you use the calculator and the lengths you recorded to find the total distance in feet around the edge of the pool? The value you find is the called the PERIMETER of the pool.
What is the PERIMETER of the pool?
Describe how you calculated PERIMETER.
PERIMETER tells you the the length all the way around a shape. However, this does not tell us all we need to know about the pool's size. We might want to know how much space the pool covers up. To do this, we need to consider every unit of space that the pool covers.
Each box in the red RECTANGLE is one square unit. How many square units are in the red RECTANGLE?
How many square units are in the red RECTANGLE?
Use the AREA tool to confirm your answer.
Think about the lengths of CF and EF that you measured before. How do they relate to the area of the RECTANGLE? Can you write an equation relating the three values?
AREA tells you how much space a shape covers.
Watch the video and follow along with the examples.
Challenge! I want to add a hot tub next to the pool. The hot tub is shown by the blue RECTANGLE.
What is the perimeter of the hot tub? What is the area of the hot tub? You can use the DISTANCE OR LENGTH tool and the AREA tool.
What is the perimeter of the entire shape? What is the area of the entire shape? You can use the DISTANCE OR LENGTH tool and the AREA tool.