Priručnik: CAS kalkulator
Dobrodošli u [url=https://www.geogebra.org/cas]GeoGebra CAS kalkulator[/url]! Naučite kako rješavati jednadžbe, proširivati i faktorizirati izraze, derivirati i integrirati, i još mnogo toga u ovom priručniku. [b]Preveo:[/b] Josip Kličinović, 7.12.2020.
Table of Contents
- Prvi koraci
- Usporedba GeoGebrinih aplikacija
- Uvod
- Istražite aplikaciju
- Osnovno
- Definiranje funkcije
- Izrazi i varijable
- Rješavanje jednadžbi i nejednadžbi
- Rješavanje sustava jednadžbi
- Limes funkcija
- Derivacije
- Određeni i neodređeni integral
- Napredno
- Racionalna funkcija
- Volumen rotacijskog tijela
- Skiciranje funkcije
- Polinom četvrtog stupnja
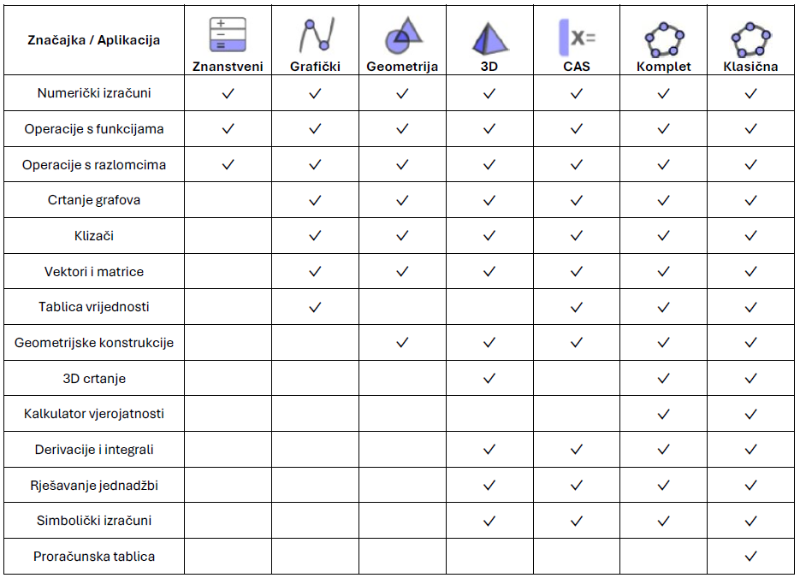
Usporedba GeoGebrinih aplikacija
S našim novim GeoGebrinim aplikacijama možete istraživati i učiti o funkcijama, geometriji, algebri, statistici i 3D na nov i interaktivan način.[br][br][list][*][url=http://www.geogebra.org/scientific]Znanstveni kalkulator[/url][br][/*][*][url=https://www.geogebra.org/graphing]Grafički kalkulator[/url][br][/*][*][url=https://www.geogebra.org/geometry]Geometrija[/url][br][/*][*][url=https://www.geogebra.org/calculator]Komplet kalkulatora[/url][/*][*][url=https://www.geogebra.org/cas]CAS Kalkulator[/url][br][/*][*][url=https://www.geogebra.org/3d]3D Kalkulator[/url][/*][*][url=https://www.geogebra.org/classic]Klasična GeoGebra[/url][/*][/list]Prava aplikacija za Vas je ona koja koristi potrebama Vas i Vaših učenika i, ako se koristi u toku ispita, zadovoljava pravnu regulativu države. Sljedeća tablica daje pregled koje su značajke dostupne u pojedinoj aplikaciji.
GeoGebra na ispitu
Čvrsto vjerujemo da će učenici profitirati od od korištenja točno one GeoGebrine aplikacie koju koriste u učionici, kod kuće, i tijekom ispita. Na taj će način dobiti najviše iskustva u radu s aplikacijom te će stoga na najbolji mogući način iskoristiti tehnologiju na pravi način u svim situacijama. Zbog toga smo izradili [url=https://www.geogebra.org/m/nauqds9v]ispitni način rada[/url] koji smo dodali u svaku našu aplikaciju. Ispitni način zaključava uređaj kako učenici ne bi mogli komunicirati s nekim ili koristiti neke druge aplikacije tijekom ispita. Ovaj je način već isproban u školama i odobren od strane nekoliko ministarstava nadležnih za obrazovanje. Pročitajte više o tome u priručniku [url=https://www.geogebra.org/m/nauqds9v]GeoGebra na ispitu[/url].[br][br]
Definiranje funkcije
Zadatak
Nacrtajte graf funkcije [math]f\left(x\right)=-2x^3+6x^2-3x+1[/math], odredite joj nultočku i odredite funkcijske vrijednosti za [math]x=-8,x=0,x=2.75[/math]. Za koju će vrijednost [math]x[/math] vrijediti [math]f\left(x\right)=7[/math]?
Upute
[table][tr][td]1.[/td][td]Unesite funkciju [math]f\left(x\right)=-2x^3+6x^2-3x+1[/math] u [i]polje za unos[/i] i pritisnite [i]Enter[/i] kako biste definirali novu funkciju.[/td][/tr][tr][td][/td][td][b][/b][b]Napomena[/b]: Graf funkcije [math]f\left(x\right)[/math]f automatski se prikazuje u [i]grafičkom prikazu[/i]. [i] [/i][/td][/tr][tr][td]2.[/td][td]Izračunajte nule funkcije [math]f\left(x\right)[/math] unoseći to u [i]polje za unos[/i]. [br][/td][/tr][tr][td]3.[/td][td]Odredite funkcijske vrijednosti za [math]x=-8,x=0,x=2.75[/math] unosom u [i]polje za unos[/i].[/td][/tr][tr][td]4.[/td][td]Odredite za koji argument vrijedi [math]f\left(x\right)=7[/math] unosom u [i]polje za unos:[/i][/td][/tr][/table][b]Napomena[/b]: Možete odabrati [img]https://wiki.geogebra.org/uploads/thumb/6/66/Numeric_toggle_button.png/24px-Numeric_toggle_button.png[/img] ili [img]https://wiki.geogebra.org/uploads/thumb/8/8b/Symbolic_toggle_button.png/24px-Symbolic_toggle_button.png[/img] kako bi ispis bio decimalna ili egzaktna vrijednost..
Pokušajte...
Zadatak
Grafički prikažite familiju funkcija i usporedite funkcijske vrijednosti koristeći [i]tablični prikaz[/i].
Upute
[table][tr][td]1. [/td][td]Unesite funkciju [math]f\left(a,x\right)=\sqrt{x+a}[/math] u polje za unos kako bi definirali familiju funkcija u ovisnosti o parametru [i]a.[/i][/td][/tr][tr][td]2. [/td][td]Unesite funkciju [math]f\left(0,x\right)[/math] u [i]polje za unos.[/i].[/td][/tr][tr][td][/td][td][b]Napomena[/b]: Graf funkcije [math]f\left(0,x\right)[/math] automatski je prikazan u [i]grafičkom prikazu.[/i][/td][/tr][tr][td]3.[/td][td]Ponovite drugi korak unoseći redom funkcije [math]f\left(1,x\right)[/math], [math]f\left(2,x\right)[/math] i [math]f\left(-1,x\right)[/math] kako biste prikazali njihove grafika u [i]grafičkom prikazu.[/i].[/td][/tr][tr][td]4.[/td][td]Usporedite grafove te familije funkcija i opišite kako se razlikuju.[/td][/tr][tr][td]5.[/td][td]Iz izbornika desno od samog unosa funkcije odaberite [i]Tablicu vrijednosti[/i].[/td][/tr][tr][td]6.[/td][td]U dijaloškom okviru stavite početnu vrijednost -2, krajnju vrijednost 5, a korak povećanja 1.[/td][/tr][tr][td]7.[/td][td]Ponovite korak 5 za [math]f\left(1,x\right)[/math] kako biste izradili tablicu vrijednosti za tu funkciju.[/td][/tr][tr][td][/td][td][b]Napomena:[/b] f(0, x) i f(1, x) automatski dobivaju oznaku g(x) i h(x).[/td][/tr][tr][td]8. [/td][td]Usporedite funkcijske vrijednosti za [math]f\left(0,x\right)[/math] i [math]f\left(1,x\right)[/math] pomoću tablice vrijednosti.[/td][/tr][/table]
Pokušajte...
Racionalna funkcija
Zadatak
Zadana je funkcija [math]f\left(x\right)=\frac{x^3+3x^2}{x^2+6x+9}[/math].[br][list=1][*]Nacrtajte graf funkcije [i]f(x)[/i].[/*][*]Odredite nultočke i domenu [i]D [/i]funkcije [i]f(x)[/i].[/*][*]Odredite ponašanje funkcije u rubovima domene [i]D[/i].[/*][/list]
Instructions
[table][tr][td]1.[/td][td]U [i]polje za unos [/i]unesite [math]f\left(x\right)=\frac{x^3+3x^2}{x^2+6x+9}[/math]. [/td][/tr][tr][td][/td][td][b]Napomena:[/b] [i]GeoGebra CAS kalkulator [/i]automatski će pojednostaviti funkciju [i]f(x).[/i][/td][/tr][tr][td]2.[/td][td]Nultočke funkcije odredite naredbom [math]Nultočka(f)[/math].[br][/td][/tr][tr][td][/td][td][b]Napomena: [/b]Nultočke možete odrediti i naredbom [math]Riješi(f=0)[/math].[/td][/tr][tr][td]3.[/td][td]Za određivanje domene, odredimo nultočke nazivnika koristeći ugniježđenu naredbu (naredbu u naredbi) [math]Nultočka(Nazivnik(f))[/math].[br][/td][/tr][tr][td][/td][td][b]Napomena:[/b] Možete koristiti i naredbu [math]Riješi(Nazivnik(f)=0)[/math].[/td][/tr][tr][td]4.[/td][td]Kako je rješenje [i]-3, [/i]zaključujemo da je domena [math]D=\mathbb{R}\backslash\left\{-3\right\}[/math].[/td][/tr][/table]
Isprobajte...
Upute (nastavak)
[table][tr][td]5.[/td][td]Koristeći naredbu [i]Limes[/i] možemo odrediti ponašanje funkcije na rubovima domene.[/td][/tr][tr][td][/td][td]Naredbom [math]Limes\left(f,-\infty\right)[/math] saznat ćemo ponašanje funkcije u lijevom rubu domene.[/td][/tr][tr][td][/td][td]Naredbom [math]Limes\left(f,\infty\right)[/math] saznat ćemo ponašanje funkcije u desnom rubu domene.[/td][/tr][tr][td]6.[/td][td]Koristeći naredbe [i]LimesSlijeva [/i]i [i]LimesSdesna [/i]odredit ćemo ponašanje funkcije u točki prekida.[/td][/tr][tr][td][/td][td]U [i]polje za unos[/i] unesite naredbu [math]LimesSlijeva\left(f,-3\right)[/math].[/td][/tr][tr][td][/td][td]U [i]polje za unos[/i] unesite naredbu [math]LimesSdesna\left(f,-3\right)[/math].[/td][/tr][tr][td][/td][td][br][/td][/tr][/table]