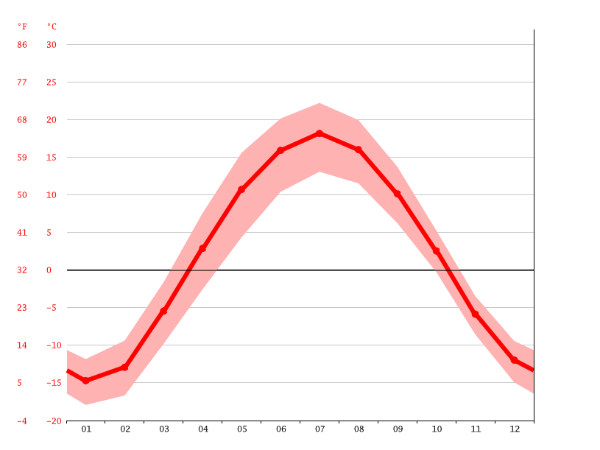
Überlege und notiere, welche Grenzen und Probleme dieses Modell des Klimadiagramms aufweist.
- Realsituation wurde in ein mathematisches Modell übersetzt. Dabei können (essenzielle) Informationen verlorengehen, z.B. Schwankungen im Tages- und Monatsverlauf. [br](Mögliche Lösung: Die Situation durch eine komplexere Funktion ausdrücken, damit weniger Informationen verlorengehen).[br][br]- Die Datenerhebungen entstanden aus Durchschnittstemperaturen über Monate, was ein relativ großer Zeitraum ist.[br](Mögliche Lösung: mehr Messpunkte, z.B. Tagesdurchschnitt, verwenden, um das Modell genauer zu machen).[br][br]- Das Modell vernachlässigt Schwankungen der Temperatur im Tagesverlauf. Dies könnte für ... eine relevante Information sein. [br][br]- Die X-Achse ist in Monaten skaliert. In der Realität haben aber unterschiedliche Monate unterschiedlich viele Tage. "Welcher Tag ist der 2,84 Monat?"[br]