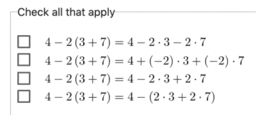Select [b]all [/b]the statements that are true.

Explain your reasoning.

Some students are trying to write an expression with fewer terms that is equivalent to [math]8-3\left(4-9x\right)[/math].[br][br]Noah says, “I worked the problem from left to right and ended up with [math]20-45x[/math].”[br][math]8-3\left(4-9x\right)[/math][br][math]5\left(4-9x\right)[/math][br][math]20-45x[/math][br][br]Lin says, “I started inside the parentheses and ended up with [math]23x[/math].”[br][math]8-3\left(4-9x\right)[/math][br][math]8-3\left(-5x\right)[/math][br][math]8+15x[/math][br][math]23x[/math][br][br]Jada says, “I used the distributive property and ended up with [math]27x-4[/math].”[br][math]8-3\left(4-9x\right)[/math][br][math]8-3\left(12-27x\right)[/math][br][math]8-12-\left(-27x\right)[/math][br][math]27x-4[/math][br][br]Andre says, “I also used the distributive property, but I ended up with [math]-4-27x[/math].”[br][math]8-3\left(4-9x\right)[/math][br][math]8-12-27x[/math][br][math]-4-27x[/math][br][br]Do you agree with any of them? Explain your reasoning.

For each strategy above that you disagree with, find and describe the errors.

Jada’s neighbor said, “My age is the difference between twice my age in 4 years and twice my age 4 years ago.” How old is Jada’s neighbor?

Another neighbor said, “My age is the difference between twice my age in 5 years and and twice my age 5 years ago.” How old is this neighbor?

A third neighbor had the same claim for 17 years from now and 17 years ago, and a fourth for 21 years. Determine those neighbors’ ages. 

[size=150]Diego was taking a math quiz. There was a question on the quiz that had the expression [math]8x-9-12x+5[/math]. Diego’s teacher told the class there was a typo and the expression was supposed to have one set of parentheses in it.[/size][br][br]Where could you put parentheses in [math]8x-9-12x+5[/math] to make a new expression that is still equivalent to the original expression? How do you know that your new expression is equivalent?

Where could you put parentheses in [math]8x-9-12x+5[/math] to make a new expression that is [b]not [/b]equivalent to the original expression? List as many different answers as you can.

[list][*]Noah says that [math]9x-2x+4x[/math] is equivalent to [math]3x[/math], because the subtraction sign tells us to subtract everything that comes after [math]9x[/math].[/*][*]Elena says that [math]9x-2x+4x[/math] is equivalent to [math]11x[/math], because the subtraction only applies to [math]2x[/math].[/*][/list]Do you agree with either of them? Explain your reasoning.

Identify the error in generating an expression equivalent to [math]4+2x--\frac{1}{2}\left(10-4x\right)[/math]. Then correct the error.[br][br][math]4+2x+\frac{-1}{2}\left(10+\left(-4x\right)\right)[/math][br][math]4+2x+(-5)+2x[/math][br][math]4+2x-5+2x[/math][br][math]-1[/math]

Select [b]all [/b]expressions that are equivalent to [math]5x-15-20x+10[/math].

Write an inequality to represent this situation.

Solve the inequality you wrote and describe what the solution means in the situation.

For every $9 that Elena earns, she gives  dollars to charity. This happens 7 times this month. Elena wants to be sure she keeps at least $42 from this month’s earnings. [br][math]7\left(9-x\right)\ge42[/math]

Lin buys a candle that is 9 inches tall and burns down [math]x[/math] inches per minute. She wants to let the candle burn for 7 minutes until it is less than 6 inches tall. [br][math]9-7x<6[/math]

A certain shade of blue paint is made by mixing [math]1\frac{1}{2}[/math] quarts of blue paint with 5 quarts of white paint. If you need a total of 16.25 gallons of this shade of blue paint, how much of each color should you mix?