Mi propuesta Geogebra
Libro creado para la materia de Sistemas de Álgebra Computacional de la Especialidad en Tecnología Digital para la Enseñanza de las Matemáticas de la Universidad Nacional Autónoma de México en la Facultad de Estudios Superiores Acatlán. Profesor. Esp. Rodolfo Maya Mendoza Alumnos: Reyes Arturo Balderas González y Mauricio Daniel Victoria Martínez Tema: Teorema de Pitágoras
Tabla de Contenidos
- Capítulo I
- Pitágoras
- Introducción
- Introducción al Teorema de Pitágoras
- Capítulo II
- Demostración 2. Teorema de Pitágoras
- Demostración 3 del Teorema de Pitágoras
- Capítulo III
- Demostración 4. Teorema de Pitágoras
- Demostración 5. Teorema de Pitágoras
- Capítulo IV
- Demostración 6. Teorema de Pitágoras
- Demostración 7 Teorema de Pitágoras
- Capítulo V
- Teorema de Pitágoras
- Demostración 8. Teorema de Pitágoras
- Ejercicios del Teorema de Pitágoras
Pitágoras
Pitágoras nació en la isla de Samos, Grecia, en 570 a. C. y murió entre 500 y 490 a. C. en Metaponto, Italia. Fue un filósofo y matemático muy reconocido, fundó la escuela pitagórica en Crotón, sur de Italia. No se conocen escritos originales de Pitágoras pero muchos de los conocimientos de la escuela pitagórica se le atribuyen a él, como la comprobación del conocido Teorema de Pitágoras en triángulos rectángulos, aún cuando ya los babilónicos conocían este teorema mucho antes en el triángulo rectángulo particular de lados 3, 4 y 5. También se atribuye a Pitágoras el descubrimiento de los números inconmensurables (números irracionales como [math]\sqrt{2}[/math]), entre otros conocimientos. La escuela Pitagórica daba significado a los números en el mundo real y en la música, consideraban que los números gobernaban el universo y les atribuian cualidades misticas[br] (Ávila, et al., 2016).
Demostración 2. Teorema de Pitágoras
Demostración 2. Teorema de Pitágoras
[size=100][size=150][right][/right]Esta demostración ilustra un acercamiento al tipo de procedimientos que se utilizan en la geometría deductiva desarrollada por los griegos, con Euclides quizá el más notable quién sitematizó el conocimiento gemétrico de su época, a diferencia la geometría empírica conocida en la antigüedad por los babilónicos y egipcios para situaciones particulares y prácticas. Teorema de Pitágoras: En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. [br][br][center]Hipótesis: Sea un triángulo rectángulo [br] de catetos [i][b]a, b[/b][/i] con hipotenusa [b]c[/b][br][br]Tesis: [math]a^{^2}+b^{^2}=c^{^2}[/math][/center]Revisa el GeoGebra que se encuentra en el Applet de arriba este recurso te ayudará a seguir y comprender los pasos de la demostración del Teorema de Pitágoras que se muestra a continuación: [/size][/size][br]Arrastra el orden los puntos [math]A_1[/math], [math]A_2[/math], [math]A_3[/math], [math]A_4[/math], [math]A_5[/math], de las figuras 1 a la 5, al área del cuadrado más grande que tiene como lado c, podemos observar como la suma del área del cuadrado de lado [b]a[/b] y el área del cuadrado de lado[b] b[/b], caben perfectamente dentro del area del cuadrado más grande de lado [b]c[/b].[br]
Demostración 4. Teorema de Pitágoras
Demostración 6. Teorema de Pitágoras
Teorema de Pitágoras
DEMOSTRACIONES DEL TEOREMA DE PITÁGORAS
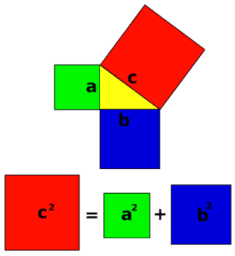
La Geometría es y ha sido uno de los bloques princiales que conforman la materia de matemáticas en cada una de las etapas educativas, por tanto, es impredescible estudiar su componente visual, eso incluye al Teorema de Pitágoras.[br]La demostración en matemáticas, juega un papel fundamental en la validación de resultados, ya que con esta herramienta se construyen razonamientos lógicos que le dan legitimidad a los trabajos realizados.[br][br]Por muchos años se le ha atribuido a Pitágoras, filósofo y matemático griego, el enunciado y demostración del teorema geométrico que lleva su nombre, el Teorema de Pitágoras, el cual expresa la relación entre los cuadrados construidos sobre los lados de un triángulo rectángulo.[br]El enunciado que dieron los griegos al Teorema de Pitágoras es el siguiente:[i][b] el área del cuadrado construido sobre la hipotenusa, de un triángulo rectángulo es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.[/b][/i][br]El enunciado moderno usa términos algebraicos: [b][i]en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.[br][br][/i][/b]Euclides, según su interpretación al teorema, dice que el área del cuadrado cuyo lado es la hipotenusa es la suma de las áreas de los cuadrados cuyos lados son los catetos.[br][br]Existen demostraciones del Teorema de Pitágoras bastante elaboradas desde el punto de vista matemático, siguiendo un razonamiento puramente abstracto y fundamentado en las leyes de la lógica. También podemos encontrar demostraciones de este resultado a partir de otros. Y, cómo no, es fácil encontrar demostraciones puramente geométricas . En este trabajo vamos a ver dos de ellas.[br][br]Una de las demostraciones geométricas más conocidas, es la que se muestra a continuación, que suele atribuirse al propio Pitágoras.[br][b]A partir de la igualdad de los triángulos rectángulos es evidente la igualdad [/b][b]a[sup]2[/sup] + b[sup]2[/sup] =c[sup]2[/sup][/b]
[br]
PLATÓN.
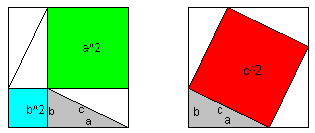
La relación que expresa el teorema de Pitágoras es especialmente intuitiva si se aplica a un triángulo rectángulo e isósceles. Este problema lo trata Platón en sus famosos diálogos.
[br]
EUCLIDES.
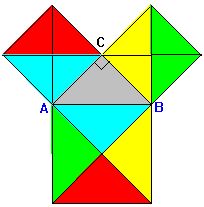
La relación entre los catetos y la hipotenusa de un triángulo rectángulo, aparece ya en los Elementos de Euclides.[br][b]Elementos de Euclides. Proposición I.47.[/b][br][b]En los triángulos rectángulos el cuadrado del lado que subtiende el ángulo recto es igual a los cuadrados de los lados que comprenden el ángulo recto.[br][/b]Para demostrarlo, Euclides construye la figura que se representa a la derecha.[br]La prueba que da Euclides consiste en demostrar la igualdad de las áreas representadas en el mismo color.
[br]
PUZZLES PITAGÓRICOS.
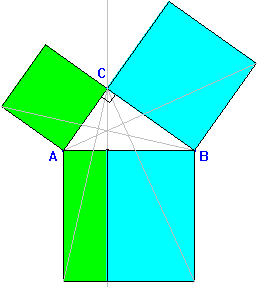
A continuación se presentan algunas demostraciones visuales del teorema de Pitágoras en forma de[br]puzzles. En todos ellos, las piezas en que se han dividido los cuadrados construidos sobre los catetos, completan el cuadrado construido sobre la hipotenusa. [br][br]1.- Los siguientes disecciones son válidas para cualquier triángulo rectángulo. Se han ordenado de menos a mayor número de piezas que lo forman.
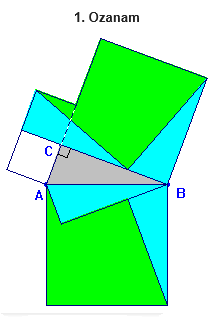
[br]
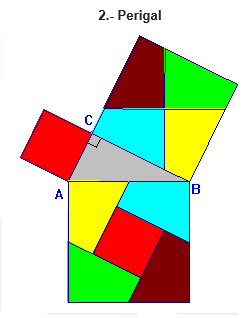
[br]
DEMOSTRACIONES ALGEBRAICAS.
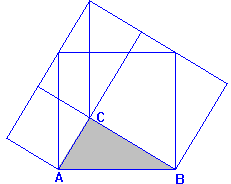
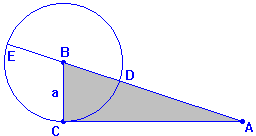
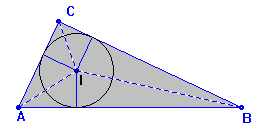
Valiéndose de la construcción que se representa en cada caso, se han dado a lo largo de la historia excelentes y originales demostraciones, no tan visuales como las anteriores, pero si tanto o más elegantes.[br]Estas son algunas de las más populares.[br]
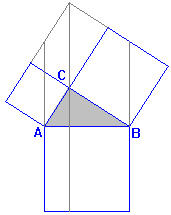
[br]
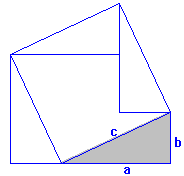
[br]
[br]
[br]
[br]