Terme in 8

herr-fischer, Sep 12, 2025

[b]Die Lernumgebung ist konzipiert als Lernbegleiter für den traditionellen Unterricht mit Phasen entdeckenden Lernens in digitaler Form (Unterrichtskonzept: Entdeckendes Lernen mit mathematischer Kommunikation + Differenzierung + Feedback). [/b] Hinweis: Bei Übungsaufgaben mit anschließendem Textfeld sind die Schülerinnen und Schüler gehalten, die Aufgabe schriftlich (z.B. im Heft) anzufertigen. Mit Hilfe des Textfeldes (ein Buchstabe muss eingetragen werden, dann wird der Button „Antwort überprüfen“ aktiviert) kann die Lösung überprüft werden.

Table of Contents

  1. Terme darstellen
    1. Terme am Würfelturm
  2. Terme addieren und subtrahieren
    1. Terme zusammenfassen
    2. Terme addieren und subtrahieren (verschiedene Variablen und höhere Potenzen)
  3. Terme multiplizieren
    1. Terme multiplizieren (verschiedene Variablen und höhere Potenzen)
  4. Summenterme addieren und subtrahieren: Klammern auflösen
    1. Plusklammer und Minusklammer
    2. Zusammenfassende Übung: Terme darstellen, zusammenfassen, multiplizieren, Plus- und Minusklammer
  5. Ausmultiplizieren und Ausklammern
    1. Ausmultiplizieren
    2. Ausklammern

1.

Terme darstellen

  • 1. Terme am Würfelturm

1.1.

Terme am Würfelturm

Sichtbare Quadrate
[b]Ein Würfel liegt auf dem Tisch. Du kannst ihn von den 4 Seiten und von oben betrachten. Das Quadrat am Tisch ist verdeckt.[br][br][/b]Zähle die sichtbaren Quadrate.
[b]Du kannst den Schieberegler betätigen und dir die ersten 10 Stockwerke betrachten.[br][/b] [br] [br]
Tabelle für die Anzahl der sichtbaren Quadrate
Stelle dir nun x-beliebige Stockwerke vor: gib die Anzahl der sichtbaren Quadrate mit Hilfe eines Terms an (Tipp: x steht für die Anzahl der Stockwerke).[br][br]Ergänze die Tabelle im Heft. [br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABnEAAADQCAYAAADYi0TYAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAAEqFSURBVHhe7d3vjxRV3v//M9/7oIC3uFxjGEjWqIHIjG4UNsFEZwRjLiPugBpjAkEGjMm1rsw6aDYbBR1018SsMBhJzCfiwALRmB0ESSBx0FwIkjHRaAJjjPHyForIH8B3XqfPaU7XVFX3/Oie6jPPR1JwqrqmuqpOV3V1vet9TsuVUQYAAAAAAAAAAACF8v+5/wEAAAAAAAAAAFAgBHEAAAAAAAAAAAAKiCAOAAAAAAAAAABAAZX7xGlpabETAAAAAAAAAAAA0FguXFOBTBwAAAAAAAAAAIACGpOJkxbpAVAcHKtxol7jRd3GiXqNF3UbJ+o1XtRtvKjbOFGv8aJu40XdAo2Rd6yRiQMAAAAAAAAAAFBABHEAAAAAAAAAAAAKiCAOAAAAAAAAAABAARHEAQAAAAAAAAAAKCCCOAAAAAAAAAAAAAVEEAcAAAAAAAAAAKCACOIUSGdnp2lpabHDyZMn3dSJ8cvREBPtF79d2l8AAAAAAAAAAMSKIA4AAAAAAAAAAEABTUsQZ9OmTRWZIvv27XOvAMBVW7duJfMqEj///LPZvXt3RcahhoULF5o1a9bwPdDEvvvuO3usUrczQ3he1oDmEdZbrcOOHTvcX6MZ6HysOmtvb6+oR52f9R2s72I0h7D+xjtw3DYPrqHilFWvOjdrul5Hcem7Mqy7iZxT1YKM7nvqWA4/A3wfA5iUK46KwWjdXLhw4cqcOXPK76ehtbXVvTqzdXR0lPfJ0NCQmzox4f6NifaL3y7tr5koxnpNGhkZudLW1lbe1plQ3zHX68DAwJjzftqg74Lh4WH3V/Hw2xejvr6+ijrMGnQ8x1a3fttmksHBwYp6jXX7Y922sN5qHXSMx8JvU6xq+a7le7Z5hPU23oHjtjn09vZW1FvWwDVUc6nl2ljnap2zY+S3sVnpflPyu3S859Tu7u6Kv08bmvH72K87gPrKO9Za9M/oizYqLG60bhR13rhxoy2PnrjMyMiILY+eLM2yZctseaZSVP7o0aO2PNn94etT6l2njaQnGpYvX27LHR0d5siRI7Y8kzTqWJ0uhw8fNo899pi5ePGim1ISe33HWq96gnDt2rVurHTe7+rqMtdcc40dP3v2rNm/f78ty+hFszlz5oxZsGCBm9L8Yq1bPV22a9cuN2ZMW1ubefjhh91Yet2eO3fOzJs3z01pbrGfi5P0xOCiRYvGnJtj3P5Y69Zvl87DGzZssOVq7rzzzmiuz2M+ZpPfteH5+NKlS/Zc7Y/d2M7FEmPdjvfJ7wMHDtjrJxkYGLBZHDGI9bgNr6F0THZ3d5v77rvPjsvXX39tXn311fK9ktiuj2OtV2XZbN++3Y2NvTZ+6623ynUqMR2rXjPXrc67PT09buyqvr4+s2XLFjeWL/n7SL97b7vtNlvW97F+GzXrcR3zdRRQJLnH2uhES8VgtG4UcfbvpacPfFnR6pmOTJzqyMRp3LE6HcIn0vTUWX9/f3mcTJzmo4yq0YvT8rZlnef1FFIt8zUrv10xCc/FGrKeJoy5bv02zRT+GiWsz1i3P8Zt07Hot4vrp7gkv2vTzsdqCUHXVX4evmfjEn4GYju+Y6zb8BpK9Zb3NL7/7tXANVSxJa+N9Ts2Tfj7VvWv83NM/LY1E9VBeKx1dXVV3JeoNRMnvL+ZdWzrvXQs+/ma6Zzt1xlAfeUdaw3tE0dZFD7qrIi0njoYPbnZcUWraRcSmLn05It/cknnB2Xd3HzzzXYczWnPnj3lJ39HL1DNzp07bTlp8eLF5t1333VjpSeKUWz/+te/XKn0dFrWU4Sq27DeqdvmpCxqnyn88ssv2//RXC5fvuxKiM1rr71W/q7t7+9PPR8r6ybMjKQ/hrjoyW99BvS7OutaC8Xx0UcfuZKxGTi6VsqiaywvfLofxRNeG6ten3zySTdWSdP1W1d03Or3EqbXo48+Wr7O1TGn3yu+1Yjx+Mc//uFKxp6L045tfR/rNWVFi95X90kBoBYNDeK89957rmTM448/bv/XF5x38OBBV8qmE5xSizTogtXTiTbZcVy1TsOS89cy5J1g9ZrWKdmZ6GQ6JtSPLC0z7BBNZU2r18leN9P9e2lb8mjfhuum/T1RvgPAcHlz5861+24i2+rrI1yeBtV7tQ4F9bd+ft+cwZdfflnxmdE4pp5uQOhYiamZj5nqiy++cCVjnn76aVdKt3LlSlcq/aBBsYU3A1evXu1K6e655x5Xom6bkb7rfDO4CsZm3ZRA81i6dKkrodnpOtzf2NUNobzjU821DA8P67G+GdkccazCIPtf//rXqJqjjVV4fXzXXXe5Urq8AA+KJbw2/stf/uJK6cIm19TEGqafguBDQ0M1N5uWpOtl36Slvo+zHnDznn32WVeqvE8KTER4/1L3UKs9rKPPp5+/2mcVBVNKyKl/apzSvP17KLXQC5t3UFNr1SSb00o2D5A26PW0NNUwZbLWQe+fpGUr5TJt/uTg1zlNuD56nzAdM2vIasImnGciwnXJSgUWpZb6+bQPJkqfA30u/LLSBqW0Jus/jfZvrXWbtf/C99F2JZuq0JD2WWgE//6x0ecsuU9rqe9YxFivqj8N6gxdx1A1fh/Eth9i3CbVp6/fWsRYtzHWaxp/jaXvQH8c+22Pdftj3Lbw+7TWZkFiE2O9hr8VdJ08U8VYt7XQbx7/+0Tn6hjFWLfh71RdI1fj541pP8S2PToWx1tP4T2sWn4nNYvx7IOi0Pdnsg7C+1y1XDeFzeTV8n2s9/Pz13IftAj8+qKYar03G/4m0Gcv6/40po+vnzQNy8QJs2zC7Bs9XTL6BWbLoycy26n5eGzevNlGvEcvhuwT/KMfSNtBXPgeej0tTXX0Q27nzxvC5YxeJJv58+e7sau0Dv7JC80zetI2oxdk9u/1v8Y1XfSklOavRp0ZqoPS5PK0zorse8o0qUczdErx9Ov83HPPpUZy9bSB7/hN87755pu2PF5a9ooVK8pPaOvzoDr0daB61TbriZUw/TyN9oWyZfwTafo7/7nw9RHWqfZxtQypX3/9tdxUhZanz5qGWbNmuTkwFfT0aCydJ6NE9alBWTbVngwNzzH+3IPiUn36+q0mzKQMv79QfMpa9U8VqslDnvBuXp999pkrISaffPKJK5mKTtExM7zwwgvl30+vv/66/R/F9+CDD7qSMZ9++qkrpQuvj7mGKq5vvvnGlWoXtjrx7bffuhKmw7Zt2yZ9jRu20nLrrbe6Urbw/XQfFJgsZZH5e+u6P512b133S5944gk3Zsw777xDCzjNxgVzciM9U2H0oqP8Hskod/gUWbVsjqEgajjHPXmUlU0RRsM173iFWUIa0p6USc6j8TTJ+ZL7QMKncrS+ejojLSqqaeH+1HYm+dc0TFRYL1q3pPDpkbR9U6vuoGO3vG0O94+GtHXSUw/+dX2WsqLKyc9Rsj7C1/121vJERSP49ZoJwnpIq++YzKR6TRM+OaJzQkxmct3qHBx+V2R9Xzej2Os1PP8mv//89Fi3P8ZtC8+xKqt+da4Nryd1PaTvWh2nWddPzcxvZ0zCa2N/Lav60zWw/52kQedh1XuM9Sp+O2eS8Bwd23VTKMa61bHqj0/9n3dchr+TdQzHIrZ6VR36bap1u8LzN3VbPMnrpmrC+tT5uRYT+Zvp5NcVxRW2cJT2/RLeLy3K/U2MlXeslafmzTRZYTBAPyKS9MEKf2ikBTi88IJVQ95Fa/LLNG+5Sfrb8Idt1gdc26aTr9Zf/+fRDyq/vLTAS3gS15C3vuGXSto+CJczGeE6hzffwgDZZA/+sO7zvry0P/x8GpL7O6zvtBNWUngCS34xJz9n1eq2kfw6zQRhPRSpDuphJtVrUvJiYzzn6mYwE+tWdajvjPB7NLabTDHXa3hdlvZwhd/2WLc/xm0LrxvDwGrWoGM368GkZuW3LSbhNbSO0+RvieSg+Sfz4FVR+e2bScK6ju26KRRr3Yb3R3Rcajz8rtVvoPB3eNo9lGbmtysmfps01HJMhtfItQQJmoXfpmYXXjfVUj/htVXePa1QeB6v9W+mk19XFFt4rzb8/R0mFsT2nRIbX09pGtKcmlK0vGeeecaVrlL6VtiZUtj0WjV5ncZpuaMfTjdmzE8//eRK1anJs9EvX1vWMpRimUbrrc5Bf/nll6qdhN52222uZMylS5dcKd3owZab0nnLLbe4UmWa9VRTE2mjF5a27Jtu0/upiTUZvfgwf/7zn215ItTMjm8GQO+T1zSP9sfoF50bG+vYsWOuVKqXammBf/rTn1zJmAMHDrhSumqdsgOYGJ1THnroofJ5QE050mRTc1JTlr6DRH03qLlKfY+qPDAwYOsWzUHXQDom9b389ttvk2YfGd9Enq5v+/r6ykNXV5edLjp21dRt2DwIisd/d4qOWzUnrHOu6nPINSPc29tbboZJ869ataqimUs0H9Wfbzq62m9GFJN+q+r41LGp41LXTNddd135Omr58uW2ORx9D+t4rnafAdMv/A5VU+x5dAz7e02Ig7+2klqamwbqRd0U+Pumu3btKl/zrV+/3v4v+n2H5lT3II5u+PuLTF2E3HPPPbacpA+a99Zbb7lSddUuWidy42H37t0Vfdz4ciOpr6A8s2fPdqX60v778MMPbVkXmPqBqGCO/9F46NChSd3cUd8/3u233+5K2e6++25XGitsF/zGG290pWzhPg6/dNOoTw8AU0s3BxctWlT+EaMbEWFAH81PNyc2bNhQ0/kdxRBeA7388stVr0fQHI4fP+5KpeCNbvCfPn3atp/tB/URODw8XHHDX0F2NAcdt/oePX/+vK1P3yedHkQ7depUxYNQYXvoaD4vvfSSK+U/0Ihi+/3vf2/uvffe8jk3ja6frrnmGjeGInvqqadcqXTjNKvfXd1QfeCBB9wYAEy9vXv32nvZomu+sJ/T/v5+ft81sboHccKnEPKyI/Qh8lkzuqFXrbN5ycvKmCjdVNy4caMbq70jXz1NrnVWgENPI8+dO7f8JI0fenp63NzV3Xzzza40/fQjUE/xiX4g+qCcngqa7MEfZiRN9imyMCNJ+zq5/9OGUFZGkz/5AZg6Ol/qKW8fENbFBJkazU0XiPpe0PeFvp91U0Lf5zofq6yLR31XorjCTFs9URo+YIPmpqe4r1yxzSjb4E3WU6K6rtMDOp6O4bSOUVE8Ou9mfY/q91f4g556bV5k4cRB18G6NtLNfrXooWsnZeYowK5B18U6plXXujdxxx13kBlZcPpe1THpKbtK94V27Nhhj1v9r3FlWUmYuQMAU0nXfbqXLbrm2759uy3re4Xfd82trkEcH9jwqn1YwvSusAm2RvHN+ni6mKolA0PbqKfJ9UWtCzFdbPkbk7FQk2nhU0Iq6ym/qVRL9sydd97pSlMvq7k9niAHppZu5ut8qfOkbiipqS0uJpqfHtTQ94Ke+tYNYz0NrhsR/gENXTwqmxPFpRsKOi71Ha/mVDEzKZAT3oj69NNPXQlFVi27Rj/ow2zXr776ypXQTP71r3+5kjGPPPKIK6GZKICq62DRNdK5c+fstZPuOygQoEHXxbqW0jWy6CZceK8ExaRAevj9qftCephJgRv9r3H99lFLJ2FT+2h+/veO+OargOmk75RksJiHZptfXYM46qMkDGYsWbIkNRvCD2EGjL7gsjIj6qXWfnBC/iLMb6f+Tk/O+Kdo/KAnH/WEcrP65ptvyvtGVJ6Op4F+/PFHV8qXVgfVhptuusn9NYB6UKC8vb29/CSIbhSfOHGCJtQiphsRugnhn/5WNidPfxeTnhD1afaTbSoVzS/MtP7iiy9cCUUTZotff/31rpQtrNewiT00B11H+eYudQ2VlVGHYgv7Wn399ddzv291jexbH9F3dPiALIpJN0l1b0E3T8NztO4T6X6QgnY6dsMWScL+jtGcJnLdTAsFqCd9vj7++GM3VhL2I47mVNcgzvPPP+9KE7Nnzx5Xqr+J9oMTXoTpqQs1UaEnZ/xTNH5oZjr4/dN92jf+YkRZS1P5xfP999+7UrYffvjBlapL1kG1gRtWQP3oXKEmBPxNYv0gVRv9k22SEcWncytP9Rdf2ORrtYduQuF0njyMx+9+9ztXQpGNN1u8SM01Y/zCmy80xdSc9BCkfzCy1kBc2Cds2Acsikv1qoCbmsoLmzJVxrq/5xA+IPFf//VfroRmFTZtWeuDx2G/zLWcC4DxUJKCTzbQ940ocYKmOZtb3YI4+iEfZm7oqYNaBt/3iqhpskaYaD844UWYvPjii66ULnzaopm88MIL5e1UJ8caRNP++c9/2vJUqCXzKm8fLl261JWad18DMUoGcHRDX9kZBE6bk87VytrQUOsToWGnvDzVDxRf2NTWtdde60oomvDa9+uvv3albJ999pkrTb4vSjTeBx984ErG3HXXXa6EZnL58mVXMmbhwoWuVLtGt1SC+tBvI7U8I3pAlofamt8f//hHV6ot2BreSA+bYgOmgn6j+8QEPfQR9ndJ05zNrW5BnPfee8+VSjfs9NRBLYOaMPNRQkUN650yrC/QifSDI+FFmJ4qr3ZDstbsniJRszc+mOY7wdLgv2jULNJkmsYJ+7j5/PPPXSlbMh0wdOutt7qSMQcOHHAlANMpGcBRsJ62WJvbt99+a7M2NNSacRsG1rlxWEzJJkbzhlA4nWZJi0k3/dQkj87FGmpx9uxZVzK0219g4Y38999/35WyhVnv3DRsPuFvyVp/r6K4avntm0RQvfj0MLN+/+Q5ePCgK5WazEPzCzNj8+5Zef/+979dyZh7773XlYDJ03X/pk2bbFlBYvVzqms+nzCh+zLqoxhN6oqjYjA6KRcuXCgvT8Pw8LB7pTb9/f3lv21ra3NTS4aGhsqvdXR0uKnZNI+fX3+b1NXVVX49+V7VhOtS7W/7+vrK82rQeFK1dQ1V2w/+NQ0TpXocPejtMvT/yMiIe+WKrVO/fL2meSci+VnJ2+5wmzUkt3s8yxJtQ2tr65Xu7u4x81bbv9PJr9dMUOR6mGqx1mt4jtWxNhPFVrfhd4OGgYEB90o2nWv9/PqOj4HfnpnIb3us2x/btun6LayzWq6PwvnD679m5rcnNuH5Na9uk5+D8f4+KzK/TTELr4nH+5u1mcVYt36bNFQ7H4vq28/PNVRx9fb2lrcr7V6Pl7yOjulcLH67ml14/y6vPkPh/by8YzX5GWiW6yy/vii28HM4ODjoppY+d7VeM2J6+TpKU5dMnLAvm9GLjnE/6bV69WpXKkUJ69Vm30T7wfHmz5/vSvnrqffRE8ujB5ObUlv/L9MtbENRTaiFT0+rTke/zGxZ82jeiUj2lfA///M/qU+uaJpey6Nlhc3xqR+frJRzLU9phKNfmDbTqNZ2SwHUTll6/ryq8x8ZOHFInrf1pE9WRqbOtXrCUOda0Xdt+B0PoP50/RYesw888EDmNaueIF6xYoUbKzXBQPZcsb300kuulF23OheHfajoO5lMnOYSNpfnW61Ac6rlt6+nVkl8Nruuoe655x5bRvGsW7fOlUr9DKb1E6i6Vkasv8eizwLn4niELRQ899xzNX8GuM7CVNG9Z99Uo677wqxd/YZ/55133Fjpfmne9w+KqUWRHFtwHdW60UlR+67+hs3AwMCEUkR1U8g346UTm7/5pxPh8uXLbVk/QNSvQh6dIP2HeGhoqNxhmH7gqONeTzf/77vvPjeWTYGb8CQbLl8XVgp2+E5DdbH96quv2n2hddVJ3a+75tUFWdaywnVNU20/hB0PT6ROdfD7foLy9nN7e3v5wrK/v982tTZeybrQD5MNGzbYptZ+++032wm2Pgv6olM9qQk3SVsv/6UYXuzq8+PrNrk80ckt2WzfeD9njTSVx2pRKNgWppV7Cnb684D/XCTpcxJDR4Ax1mv4XaDjbDxN8sRSrxJj3SbPtaKHNtQcgO//Rs0xqTkBf66ViV4TFFGM9VqryV5jFF2sx+yiRYsqjsfkeVlN0SaPaV3/VGsuuFnEfMyGv5tE17433nijLetaSte5vu7TfoM0u5lwPlY/dLoxLHqQTs2QzwQz4Xzsf6+qecTZs2fbabqPoCYS/b0B4Rqq+NREkb9XIeH3rJoWDu9BxPYd6zVb3eq+T9hfnHf8+PHy8af7QXfffbcth/RgWvK7NObPwEz4rm1m4X1Vfa+cO3cu9bMVfkbT7oVi+uUea6MTLRWD0QlTupZf1ugHx6ZsTUSYMh4uJ5w+ejK10/JoHj9/mC4WpkeOZ0imUo6MjFSkQqYNWge//mH6mh/8emWta5pq+8G/pmG8wm3S/xrPkmxWLW/ePGqOxy8na9C+r6X+ta/DfZk3jF4wp35Ga3mf6eLXKybh/h7vkDwmm5XfnpiE9TTeIZZ6Fb9NsdG5c/TCr6LesgZ9P9TS7Foz8ds2E4V1G6NYt03XaG1Bszx5g6590q6Pmpnftljpmjasw7RBv0Nia7pH/PbFLKzfmK6Rqom1bnU+rvX3KtdQzaWWc3GM37Ge38ZmofNpWDfjGbLu2YVN62UNuh5rts+AX3cUU3iNHzajlqTPXXhfOm9eTA9fN2mmvDm1N954w5VKT4FNNKqsJ7AVmRZFqo8dO2bLRaPIuyKcyhDx6yujF1s2qqknZsLo+qFDhyrmU3bBrFmz3Fgx6Gk+/3RAshm1pGSzatrmifDN7egzo33i+f04+gVZ8xNn2tfa5/qb5PJE+1/T9boyvJrlyQcAKBKdO/Xkjs6lye9A0fl79EeqzdLU92QsT48CzUrXc6dPnzajP9aqXh/F+HRw7HRNm3btG/4mOX/+PE33NKmsJqLRnHQ+Dn+vcg0VD38u1nk361zMd2zctm3bZoaHh3O/j3U9xmcAU0XZuj6bXp+xsBm1JH3uwmbVHnvsMa4xmkhdmlMDUD8cq3GiXuNF3caJeo0XdRsn6jVe1G28qNs4Ua/xom7jRd0CjZF3rE15Jg4AAAAAAAAAAAAmjyAOAAAAAAAAAABAARHEAQAAAAAAAAAAKCCCOAAAAAAAAAAAAAVEEAcAAAAAAAAAAKCACOIAAAAAAAAAAAAUEEEcAAAAAAAAAACAAiKIAwAAAAAAAAAAUEAEcQAAAAAAAAAAAAqIIA4AAAAAAAAAAEABEcQBAAAAAAAAAAAoIII4AAAAAAAAAAAABUQQBwAAAAAAAAAAoIAI4jTAyZMnTUtLix06OzvdVHh+32gAAAAAAAAAAAAlBHEAAAAAAAAAAAAKqGFBnC+//NJs3brVZqLMnTu3IvtCg6br9cOHD7u/AAAAAAAAAAAAmLlaroyyBdeUlRudMgre9PT0mKNHj7op1bW2tppDhw6ZxYsXuylj1Wt960HNqS1fvtyWOzo6zJEjR2wZJb4upRnqc7o102cftaNe40Xdxol6jRd1GyfqNV7Ubbyo2zhRr/GibuNF3QKNkXes1TWIowDOihUrzMWLF92UUhDj7rvvdmNXHThwwJw5c8aNGTNnzhxz4sSJ1EBOGBRphhMIQZx8/rMnzVCf040vzzhRr/GibuNEvcaLuo0T9Rov6jZe1G2cqNd4Ubfxom6Bxsg71uoaxGlvby8HZtra2sz+/fvNggUL7HgaBTseeOCBctBHf3P69GlbDu3YscNm90gznEAI4uTznz1phvqcbnx5xol6jRd1GyfqNV7UbZyo13hRt/GibuNEvcaLuo0XdQs0Rt6xVrc+cZSF4wM4yqpR4CIvgCPLli2z2Tee/j6tj5yzZ8+6EgAAAAAAAAAAQJzqFsS5fPmyKxlz++23m3nz5rmxfGo+rbe312as6P/Zs2e7V0rRKA3K6PH8NA3K0EmjTJhNmzbZzKBwfo1rul6v1b59+8yaNWvM3Llzy8tZuHChXc53333n5pq4cB21TL2fH8/aPi9cp61bt7qp6bTOft40fp+F82no7Oy0y87bVv2tn9+vs4J6+ls/XePjpff1f6/99PPPP7tXKk1m3QEAAAAAAAAAKIq6NaemG+m+CbGsZtHGy69jlr6+PrNlyxY3ZuxN/s2bN1cEfbIoaLR3797MYJOCDuvXr6/otyfNwMCADfKEwn2R15yaAg+7du2yZT+fAg6tra0V09Jo/ZYsWeLG8vd5uMyuri4bKPK0zx599FFz9OhRNyVb2rZKuL1a/vbt2+36hH0jDQ0N2cwrCes16/OndVy7dq0tK7Pr3LlzY+pqKta9GUz1sYpioF7jRd3GiXqNF3UbJ+o1XtRtvKjbOFGv8aJu40XdAo2Rd6zVLRNn1qxZrlRqFi0MFEyUbvxrCPlpGlavXu2mluiGvg/g6Ma/MnvC+TWu6aIb/8rUSKPgwIoVK8oBHAVAFDAaHBy0wYDu7m47XRRomMi2hgEcBTwUUBI1QecDLnnBif/93/+1//vt0bpmZaocO3bMlYzdLk/zax/499H79vf3l/eXtne82/rrr7+a1157zQZwtDwFojSEn49qkgEcNbmXFsCZ6nUHAAAAAAAAAGBaXXFUDEanREdHR3m5Gvr6+q6MjIy4VycuXGaWgYGB8jxz5sy5Mjw87F6pdOHCBfu6n7e/v9+9clV3d3f5dZXTJN9Py/WGhobKr2mfJGm/+Nfb2toq/lZ6e3vLr2tZabq6uuzr4byDg4Pu1Up+Xg1hfYR/q3mS6+GF26NtTdZp+Lq2R/9r2Vn8vBqSku+VVY9Tte7NwK8/4kK9xou6jRP1Gi/qNk7Ua7yo23hRt3GiXuNF3caLugUaI+9Yq1smjuzcubOcGSI9PT02Q0L9mahvksOHD9etf5Lnn3/elUrrob520iijQ697r776qiuVaP18hoy25cUXX7TlJDXNpQwTUdbJwYMHbbkaZYNov4gycNRcWjLL5K677nIlYz777DNXquQzjm699dbyenz66af2/6SPP/7Y/q+6UKaPKJNFzZ6JtvPNN9/MbFpOzaD19vbacrVtVUaQ1mfbtm1uSu3URNwDDzxgy1onZeCk1WO91h0AAAAAAAAAgOlU1yCOAgTquyRsxkp0Y1833VetWmUDCeqAXkGQ3bt3T0lQRzf/R0ZG3FgpwJInfF1/F65D2PTYvffemxkckAcffND+r2DMpUuXbDlP2EyY9kNaAEdWrlzpSsYcP37cla5SHzTe7bffbpYuXWrLPlgT0r7xfdOovxov3E7tj7ztlD/96U+uZMyBAwdcKd3TTz/tSrXTeqqpN7+uWQEcqee6AwAAAAAAAAAwXeoaxBHdUFemi4IjyoBQgCNJrymTZOPGjTaYoRvxuok/Ud98840rmXJWSjXhfN9++60rlYIJ3m233eZK6Z588knlO5nTp0+bLVu2uKnptFz1gyPKHjl06FBu8MEHXNL6xfHZOT6zxmfupPWL4/vOkTDD55NPPnElY2688UZXyhYGVHxfQVnCIFQttM7r168vB3DU71BWAEfque4AAAAAAAAAAEyXugdxPAUX1KSWAhwXLlywHc339fWlBlkU0FmyZMmEO57/4YcfXMmYa6+91pVq99VXX7lSqTk175ZbbnGlyRlPlomn+b0w80Z8do4yheSOO+6w/8upU6dcqUTv5YXBlXA71bxbS0tL1SGUlUGlANV4KIDT2dlZDq709/dXzaSq17oDAAAAAAAAADCdGhbECSnjRAEEZauoCTFlrwwPD9tMnfCmv5oaU785k1Ete2Y8Zs+e7UoTpyBFGMCRMDsmyx/+8AdXGtsvjs/O+eMf/2j/1/71GU/JfnF8E2thU2pT4aeffnKlSmrebTweffTRiuyYMOhUL1nrDgAAAAAAAADAdJqWIE4aZaIoU0c38MMm1/72t7+5Uhy0fQrghMEqNSNXrfk47R81lyZhvzhhkCsMmPisnLBfHL2HDx6FmT1Jyn4ZGhoa13DTTTe5v54cH5Dy+0dZWeorqVbTue4AAAAAAAAAAEylwgRxPDW79vrrr7uxyfdZcvbsWVeavB9//NGVJkcBCmWYqDk576GHHhrTf02SD8yE/eL4TBvfH46X1i9OmPFzzz33uFK6ZcuWjWvI689nvNQHzocffujGagtyhdLWL2+YynUHAAAAAAAAAGCq1C2Io35GlCUykX5tdGN9Mm644QZXMubXX391pXxhAOXOO+90pVJQyQv72pkoBVvOnTtnM2vUnJzvE2hkZMRs3rzZlrPcf//9rnS1XxyfaeMDPF5avzjvv/++/T8Z8JGlS5e6kjGXLl1ypcZTs3rqA0efgVqDXEVZdwAAAAAAAAAAplJdgjgK3ChQsGrVKrNp06aqGSZJk+1oPmxWTFkr1d5fr4cZP/Pnz3elUjNm3oEDB1wpnQIr6jR/7ty5ZuvWrW5qpYULF1Zkfuzdu7fmpsPCwIz6xQnX2/eH46X1i+MzeNL6w7n11ltdqfp21lO4v2sNchVl3QEAAAAAAAAAmEp1CeKoqS4fmFAfLC+88IIt1+rgwYOuZCr6x6mVskx8/zFy7NgxV0oXvq73C7NUwmbHFDDJCzC999579n/f70wtFGyptekwzeuDGuoXx2fYSBi48sJ+cXzmjvim1kLJ7QznT6N1VEBKQbpq805GLUGuoq47AAAAAAAAAACTUZcgjoINL7/8shszZteuXbaJrGoZNsosUQZLT0+Pm2LM3//+d1e6yt/Ul6yb8C+99JIrGXuzPiswoul63Uu+nwI63d3dbqyUxZKW2aP10HZ669atc6Xq1HRYb2+vG8tvOuzuu++2/yurJqs/HC/sF0eZO97KlStd6SrVWbgOTzzxRGZ9ad3Wr19vs2O0zVPVV1Aarde7777rxtKDXEVddwAAAAAAAAAAJqPlyihbaGmxE9zolFBwJAxsiDJd2tvbzY033uimlPox+eKLLyo67BcFT3bu3OnGrurs7CzPq+U9/PDDtqy+cBQs8lRW9oYo8KPl3XfffXZcPvroI7t+PnMm6/1043/RokXl+fyy1IyX1l1BhXA7FVDYtm2bGysFeJYvX27LyqQ5cuSILSdpv/jm0RQsSutPSO+1ZMkSW9Z6aJ2S7+dpva+77jpb9vNmLVc0v/atX4fkPvvtt99s4CjcZ2nLq3V7Pf/Zk6zPn4J727dvt2UFrZSFpOCNN1Xr3gzqcaxi+lGv8aJu40S9xou6jRP1Gi/qNl7UbZyo13hRt/GiboHGyD3WRidaKgajU2ZgYODKnDlzysuvZWhtbb0yODjoljCWXkv7u46ODjdHyYULF650d3enzpscent73V+lGx4evtLW1pb6t+GQtpyhoaHy68l1DI2MjFTsq/7+fvdKpeT+zNtXyXXOWqanfaZ1DP8ma9C+1fxJtW6vFy4zT7gtXV1dbupVU7HuzcBvA+JCvcaLuo0T9Rov6jZO1Gu8qNt4Ubdxol7jRd3Gi7oFGiPvWKtLc2ohZcP88ssvZnBw0GZGdLg+XULKmtB0ZZRovvPnz6c2+eXptf7+/op+b5SR45sa85SpocyaoaEh+96aJ6Rxvaea1krLZAmpw/3Tp0+bgYEBm8Ghdfa0Hlq+3qfacvKoSbRqTYdJmG0kd9xxhyuN5fvF8cL+Y9Jonylzxu+zcB+L9pnfVu3bMBum3pRV5fd7Wv84RV53AAAAAAAAAADGq67NqQGYehyrcaJe40Xdxol6jRd1GyfqNV7Ubbyo2zhRr/GibuNF3QKNkXes1T0TBwAAAAAAAAAAAONHEAcAAAAAAAAAAKCACOIAAAAAAAAAAAAUEEEcAAAAAAAAAACAAiKIAwAAAAAAAAAAUEAEcQAAAAAAAAAAAAqo5cooW2hpsRMAAAAAAAAAAADQWC5cU4FMHAAAAAAAAAAAgAIak4mTFukBUBwcq3GiXuNF3caJeo0XdRsn6jVe1G28qNs4Ua/xom7jRd0CjZF3rJGJAwAAAAAAAAAAUEAEcQAAAAAAAAAAAAqIIA4AAAAAAAAAAEABEcQBAAAAAAAAAAAoIII4AAAAAAAAAAAABUQQBwAAAAAAAAAAoIAI4hRIZ2enaWlpscPJkyfd1Inxy9HQCFO57gAAAAAAAAAAgCAOAAAAAAAAAABAIU1LEGfTpk0VmSL79u1zrwAAAAAAAAAAAEAaHsT5+eefxwRtnn/+eVcCAAAAAAAAAACANDyIc/DgQXPx4kVbbm1ttf+PjIzQjwoAAAAAAAAAAECg4UGcV1991ZWMeemll1zJmPfee8+VAAAAAAAAAAAA0NAgjrJtlHUjXV1dZs2aNWbOnDl2fNeuXbapNQAAAAAAAAAAADQ4iBNm2zz++OP2/+7ubvu/qKm1ahQIamlpscOmTZvcVGP72ens7Cy/pkHju3fvzgwOJeevZchr9k2vaZ3a29sr/mbhwoU2YJXsC6gW3333nV2mlhEuT9Ma1QSd1lvrH26TtnHHjh0TCrz55c2dO7e8PJWr1ZfoPf3f+O0/fPhwef9oOQAAAAAAAAAAxKDlyihbaGmxE9zolFMwwveBo+ybX375xZa//PJLs2TJElvW6+fPn7flLLpxv3z5clvu6Ogwe/futTf/z5w5Y6elaWtrM0eOHDHz5s1zU0r0d0ePHnVjtRkaGjLLli1zYyUKOmzevNns37/fTcnm1zm5LhKuj97nxx9/NGvXrrXjWQYGBmxAJMnXp0ymThUsUpZUFtXZoUOHTE9PT8W6J/eRqK4feuihcjZWFn0+Tpw4YRYvXuymXKUgjt5L+vv7ze9+9zuzatUqO+7V6zNcFPU+VjE9qNd4Ubdxol7jRd3GiXqNF3UbL+o2TtRrvKjbeFG3QGPkHWsNy8QJs2zC7BvdqFeQRXRzX1kV46HgiQI4Co7opr4CCApshO+h1/fs2ePGrurr67Pz5w3hchRcmD9/vhu7KgzgaJ7e3l4zODho/17/a9w3G6dAh+av5uuvv7YBnOTytM4+GCYKstSrGbqtW7dWBHC0Hn6/aH20b1Rn69evd3NkUwBnxYoV5QCO6kv15JensqbJxYsX7bz6mzyXLl0yTz/9tC3rM6S/98sAAAAAAAAAAKDZNSwTR81d+Rv4+n/BggW2LGpey2ecqK+cvGbHwkwcBTh0wz8rG0VNc23cuNGWNa/P/qlVmCUkClysXLnSjZUk5xkeHk7NIEnOl9wHEmbiaH0VrEnLIFLQ5o477ijvTwWvnnzySVv2fH3KROo0zJySrH2soFsyE0ZBmWQmjppf89lSCkRt2bLFlpPCTBsFZk6fPm3LXvJ1LTOtXmLGExBxol7jRd3GiXqNF3UbJ+o1XtRtvKjbOFGv8aJu40XdAo2Rd6w1JBNHQRkfcNCN92Tw4p577ilnqiijRQGEWiiAo2yQtOCCrF692pVK89a6XFGgRE1/ecpCSQsUfPPNNzb7Q+uv/9MCOKLpClB5x44dc6V0Wl/ti7Rm1zRtw4YNbqwUIJpq4fppu7L2sfZJmK2URoEeH8DRsrICOKLXfGaW/iav3x+9roDQTArgAAAAAAAAAABmjoYEcd555x1XMuaZZ55xpasUlAiDBGHTa9X85S9/caWxtFwfEJCffvrJlapTk2dh4Gnbtm22nKT1VraMsnz0f57bbrvNlUpNgeVRYCQZ7ArdcsstrlTKmplq77//visZ8+CDD7pSukceecSV0v3nP/9xJWOeeOIJV8oWNs/20UcfuVK6devWuRIAAAAAAAAAAHGpexBHAYawiTBl3aQJmwN76623XKm6vECHpGWyVKNm2MI+bny5kbIyerzZs2e7Un18/vnnrmTMzTff7Erpkk2nJX388ceuZMz111/vStnC9/viiy9caSxl9UykfgEAAAAAAAAAaAZ1D+K89tprrlTKWsm66a6ghc+aUQZMXr84nm7iTzU1Teb70ZF33323aqBI1Pya1nnTpk22b5u5c+faduzCwfflUotqgZN6U3Nu3vz5811pYnxGk6g/o+R+SQ6+zyM5f/68K4117bXXuhIAAAAAAAAAAPGpaxDHBza8ZOf7SWEzWmETbI1Saz84SdrGRYsWmbVr15pdu3bZzKMwCNLsagli1SOgJmEAKClsng4AAAAAAAAAgNjUNYijzvHDYMaSJUtSMy/8EGbAKBBSj75e8tTaD05InfYreOO3U3/X399vhoaGKoYrV67YTvhjlZcxE0rul1oGAAAAAAAAAABmoroGcZ5//nlXmpg9e/a4Uv1NtB+cp59+2pWM6e7uNqdPn7YZR+onJhyaWS3BtLyMmdCsWbPG7JtqAwAAAAAAAAAAM1HdgjgnT56suLGvLJRaBjVh5qlpskaYaD84+rtwG1988UVXSnfp0iVXai4//fSTK6VTM3R5fF9HcvnyZVcCAAAAAAAAAAB56hbEee+991yplKGyZcuWmgY1Ydba2mr/Tk2UhX3q1MNE+8GRMCChPmHmzZvnxtLVmt1TBGEfN19//bUrpTt16pQrpWtvb3clYz766CNXAgAAAAAAAAAAeeoSxFFgJMyiUfNi4/Hss8+6kjH/+Mc/XKk+JtIPTppq2Sg7duyoucmxIli6dKkrGfP++++7Uro33njDldLdf//9rlTKrqq2r9S0nQI/W7dubXi/SAAAAAAAAAAAFEVdgjhhXzYKjCxevNiN1Wb16tWuZMyZM2dss2X1MNF+cLz58+e7Uv566n16enoqslu+//57VyqmdevWuZIxR48ezcyI0nS9nkeZTb5JNWVXKXCWFcjRPnzuuefs/ty+fbubCgAAAAAAAADAzFOXIM5bb73lSsY888wzrlQ7NUumJtg8BUGmWrIfHL2f+n5RXz55Q5gZon5zwsDMihUr7Lr6eVVeuHChfR/N9/zzz7s5S8GPImeZaNu6urrcmDFr1641mzZtsuvtt62zs9NOV4Am3A9p3n77bRsoEwXL7rjjjop9peVq+UuWLLGBHunv76+pbyIAAAAAAAAAAGI05UGcw4cPl5sN0037e+65x5bH65FHHnGlUsCjWhNc45XMHlHWx/Lly6sOBw8edH9RsnPnznJwQsEHBWz8vCprXyjAsXfvXrNs2bKK/n5UbmlpsUGMInrzzTfLGTSiptAUtPHbpn2obaglg0nZWCdOnChvv/ZLuK+03LAJPgVwxtsMHwAAAAAAAAAAMZnyIE7YP4qyW6p19p9FAY+wCa5jx47ZctEoU+TcuXOmt7e3IuChwI4yWQYGBsyRI0fK++HQoUMV8ymoMWvWLDdWLFrn06dP221IZtpoG/r6+sypU6dqzpZRIOf8+fN2edo3Pvjl6T20HxXgIYADAAAAAAAAAJjpWq6MsoWWFjvBjQIoKI7VOFGv8aJu40S9xou6jRP1Gi/qNl7UbZyo13hRt/GiboHGyDvW6tInDgAAAAAAAAAAACaHIA4AAAAAAAAAAEABEcQBAAAAAAAAAAAoIII4AAAAAAAAAAAABUQQBwAAAAAAAAAAoIAI4gAAAAAAAAAAABQQQRwAAAAAAAAAAIACIogDAAAAAAAAAABQQARxAAAAAAAAAAAACoggDgAAAAAAAAAAQAERxAEAAAAAAAAAACgggjgAAAAAAAAAAAAFRBAHAAAAAAAAAACggAodxOns7DQtLS12OHnypJs6dXbs2FFevsr1pm3w76dtAwAAAAAAAAAAyEImDgAAAAAAAAAAQAEVOoizdOlS09HRYYdZs2a5qQAAAAAAAAAAAPErdBBn27Zt5siRI3ZYvHixm1pcvnm2RjTNBgAAAAAAAAAA4kZzalPo+PHjrgQAAAAAAAAAADA5BHGm0NGjR10JAAAAAAAAAABgcgjiTJEvv/zSlQAAAAAAAAAAACav7kGcffv2mTVr1piFCxfa/mL8oHFN1+tZOjs7y/OfPHnSTR3r559/Nrt3766YX0N7e7vtn0av10rz6m/0t345c+fOzVxX3w/OkiVL3BRjenp6yn+rIU/a+2nQtuTtm5D2zaZNm8Yso5Z9LOF+87RO2m5N0zLSZO33ibzvd999Z6fpf21L+HlRWdPyPgMAAAAAAAAAAMSm5cooW2gp3cB3o5OmG/y6SX/mzBk3JVtHR4fZu3evmTdvnptSor/3TZQNDQ2ZZcuW2XLo8OHD5rHHHjMXL150U8aaM2eOOXHihFm8eLGbUqJAhQIu0tfXZ9djxYoVucvq7u42O3fudGOVy8ji96mCEMuXL7dlvZfes9r7Ze0b0T7evHmz2b9/v5uSLW854X4eHh42//73v8327dvtuOhvjxw54sZKFKBRYCVv3aWtrc3+bbX3Vf3++OOPZu3atXY8y8DAQGZQaaaY6mMVxUC9xou6jRP1Gi/qNk7Ua7yo23hRt3GiXuNF3caLugUaI+9Yq1smzqOPPloO4LS2tpr+/n57o94PCmBouuhGvuYfLwVFVq1aVQ4k+MCIlq/307jodQVL8po8u3TpknnooYfsvArUKFiQXI7s2rWrIiNk9erVdj79jaey304NWdavX2/fT8v3+0fv29XV5eYo7Zt//vOfbqxSGMBRoKq3t9cMDg7a5eh/jWu6aDmav5pvvvmmHMDRemlYunSpHfcUwFGwxe93ba9/Xw3aFl+3+gwoWKOAU56vv/7aLjO5HeHnRBQ4qrYsAAAAAAAAAACicMVRMRidlOHh4fLyWltbr1y4cMG9UknT29rayvPq70IdHR3l14aGhtzUq7Rs//rAwICbWqm7u7s8j5YX6uvrK782Z84cOyTXwevq6irPq3JSuCyV02gb/Dx+yFrv/v7+ivlGRkbcKyXhPtaQtd7J+ZLLkXA/qz60X7OWp7/XfvLzp9WLqG7Dfdbb2+teuSp8Xy1T7532WdG0sK61b2Yyvx8QF+o1XtRtnKjXeFG3caJe40Xdxou6jRP1Gi/qNl7ULdAYecdaXTJxLl++7ErGbNiwIbUpLdH0119/3WaeKOMi/LtqlA0yMjJiy8oWyWpi68UXX6zIRsnKxlFWiZpJSza55j311FOuVMoumQrKYMla7yeffNI2ReYdO3bMlUqUMaPt1rbp/6z11vQwsye5nCRt2zvvvJO5vD179pQzcFRnaU3cier2zTffdGOlDKa8DBotU1lFaZ8VTQu3IS+jCgAAAAAAAACAWNStOTXvwIEDrpROQQAFZLZs2ZIZEEjzwQcfuJIxDz74oCuNpQDAvffea8sKdvzf//2fLSepya68vlZuuukmVzLl4NFkKVCT5+GHH3YlY95//31XKtG6qq+ZX375ZUx/NUm33XabK5WajcujwFFePYT976gpuTxh8EVBmlOnTtlyGgW0FixY4MbGuuuuu1zJmO+++86VAAAAAAAAAACIV12COAp4+OwX3ydK2I/MVAizYW6++WZXSqcg0ZUrV2ywY+XKlW5qpTDrJU1ahshkZWW7eHfeeacrGXP+/HlXqq8wcJSk4EkYwMoLunhhAOmrr75ypbFuvPFGV0o3e/ZsVwIAAAAAAAAAYGaoSxBHAQ81TeapGbPly5ebuXPn2gyS3bt3T7pJrDCYEGbJTFQYbGiEakGjpKzsHzVRpiCVOvxXsEz7uKWlpWLo6elxc1d3zTXXuNJYP/30kyuVJN8nbQjf+/vvv3elscKAFQAAAAAAAAAAqGNzagrWDA0NVQQrfL8nGzduNEuWLDELFy40O3bsyO0rpRb1yJKpt6lYZwVvFi1aZNauXWv7nFGwzPdXM1HVspomg2bQAAAAAAAAAACoXV37xFHfKqdPnzbDw8O2E/xk9omyS5SpoUDE4cOH3VTUQvtLwRsftNG+7e/vt4GzcFAzctr3U03vl3yvakM91gMAAAAAAAAAgFjVNYjjqe+XLVu22IDOhQsXzODgoOnt7S33m6NAxGOPPTbhTI2ZmOHx9NNPu5Ix3d3ddt8++eSTNnAWDvWiAFzyvaoN1foAAgAAAAAAAAAAVzUkiBNSM2IrV64027ZtM+fOnStn5yiQs2fPHluuRWtrqyuN7aulGajps/EIs5jUn1DYR86LL77oSukuXbrkSpMT9j002WbbAAAAAAAAAABAvoYHcUIK6Lz++utuzJgvvvjClaoLgxofffSRK6VTvzvqZF998KgfmaKolkH02WefuVJl0Ory5cuuZExHR0fV/nXUD9FU0PuE60ETeAAAAAAAAAAA1E9dgjhr1qwx7e3tdqiX//7v/3al6kGKt956y/6v7JXZs2fbchEcPHjQldIdOHDAlYxZsWKFK1X6+eefXSmdAlhh1s5kdXV1uZIxb7zxhitl02ehs7PT7N69u+q6AgAAAAAAAACAq+qWiXPmzBk7KIiQ57333nMlYx588EFXqk7BAZ8VoiDFpk2bbDkpDGJofjXlVg/XXHONKxlz/PhxV8r3yiuv2KbR0ihjSPtP1HfQ6tWrbVnmz5/vSqX9nLUMBU56enpsto73/fffu9LErFu3rtyXkZqEy6tfbYMCbJrv1VdfrZoxBAAAAAAAAAAArqpLEOe5555zJWODCMrI0c3+kydPlgeNK0Nj165ddr5koKIW77zzjisZuxw1l6blqpkvv3y9v1dL5shE3Xzzza5UCm5s3brVroOGtGbT1Bzc3LlzzZIlS+y84b5RQGrt2rVuTmP++te/VgRAFixYUBGYUZaOAjb+71XWvti4caOd7/nnn3dzlgIr1Zpxy6P33rlzpxsr1a/2s5Ybvr+mhdtw6NAhVwIAAAAAAAAAALVouTLKFlpa7AQ3OmkKpDz22GM1dYCvDBnd5F+8eLGbUqJAgAIiMjQ0ZJYtW2bLoVreRwEiBR6UvRNSgMUHefr6+syWLVtsOYvfR5K2nxSs8tkzIb/uCnAsX77cTlNwRe+pAEzeund3d1cETTwFYhQIyvtbvcfevXttAEhBnWSzan69atnPSQraKNhUrX617z/88MPUZY7nfZP77siRI7Y8E031sYpioF7jRd3GiXqNF3UbJ+o1XtRtvKjbOFGv8aJu40XdAo2Rd6zVrTk1NVt27tw509/fb2+6hx3ii8bVv8rAwIA5f/78mABOrZLvE1KQo7e31wZWkgGcelDTYWGfMQpgaJ3C5s88ZbRom7XuCuZoXT39nZYzODiYGsAR/b3+VtuX9rfarwp0+AweBcnC+bT/Z82a5cbGT/sza7/77dZrmqeWoBAAAAAAAAAAAKhUt0wcAPXBsRon6jVe1G2cqNd4Ubdxol7jRd3Gi7qNE/UaL+o2XtQt0Bh5x1rdMnEAAAAAAAAAAAAwcQRxAAAAAAAAAAAACoggDgAAAAAAAAAAQAERxAEAAAAAAAAAACgggjgAAAAAAAAAAAAFRBAHAAAAAAAAAACggAjiAAAAAAAAAAAAFBBBHAAAAAAAAAAAgAIiiAMAAAAAAAAAAFBABHEAAAAAAAAAAAAKiCAOAAAAAAAAAABAARHEAQAAAAAAAAAAKCCCOAWwY8cO09LSYgeVAQAAAAAAAAAACOIAAAAAAAAAAAAUUMODOIcPHzZbt241nZ2d5ewTP7S3t5s1a9aY3bt3m59//tn9BQAAAAAAAAAAwMzTsCDOvn37zMKFC82qVavM9u3bzdGjR90rV505c8bs37/fbNy40Vx33XVm06ZNBHOmmQ+wAQAAAAAAAACAxqp7EEdBGGXXrF271oyMjLipxsyZM8d0dHSY3t5e09fXZ7q6ukxbW5t7tWTXrl1m0aJF5ssvv3RT0EgnT550JQAAAAAAAAAA0Gh1D+I8+uijNrvGU+BmaGjI/PLLL+bIkSNm27ZtZsuWLTZT5/Tp0zbQo6COgjxy8eJFs2LFCgI50+Czzz5zJQAAAAAAAAAA0Gh1DeLs2LGjotm0/v5+G7hZtmyZmzLWggULbFDnxIkTFYGchx56iKbVGuzs2bOuBAAAAAAAAAAAGq1uQZzvvvvO9PT0uDFjs2uefPJJN1bd4sWLbSDHU4bOnj173NhVChT5fltUzqPmwfy8nZ2dbmo6ZQapGTj14+P/RkN7e7vtq6fWpsY0n+afO3dueRlapqZpH1UTrrPfPmUlaf399LQsJQW8du/ebecL31uDpm3dujXz/f18YQZV+PdZ+1nL03K1j8L5x7vPAAAAAAAAAABAHYM4YcCltbXVZteMlwI5Cv54r7zyiivVjwIiCjqoDx8FMcJ+fOTMmTO2r57ly5fbgEUeBYI0n+ZXNpGnZWqa+gDSPLVSZowCJWpeLsxwunz5siuVHD582PYltHHjRjtf+N6iadu3bx/3++fRvlA9a7naR6FwnymYAwAAAAAAAAAAqqtbECfM4nj22WddafzWrVvnSqVm1RSgqBdlr6jZNh+EUFBCQST14aNhYGDAdHd329dEAQtlu6TReioQ5HV1dZnBwcHysnp7e+10BTW+//57W67m119/Na+99prdD1o39S+kYdasWW6OUhBq1apV5cCNXlczdv59VdY00Txax2Qmj5835KdpWL16tZtaom3QvhA1gadtC+fXuG8aT8EcAjkAAAAAAAAAANTgiqNiMDopIyMj5eVp0PhkdHR0lJfV19fnppZoPOu1pKGhofK8WmZSf39/+fXW1tYrFy5ccK9USs6XRtP9PN3d3W5qJe2XOXPmlOfTkNyGcJ3b2trs/729ve7Vsbq6usrzq5wlnC9r/fzrGrIMDg6W59E2Z9W1pof7RH+HifH7EHGhXuNF3caJeo0XdRsn6jVe1G28qNs4Ua/xom7jRd0CjZF3rNUlE+enn35ypZIFCxa40sTcfffdrmTM8ePHXWnq/fDDD+UslQ0bNph58+bZcpL69vGZJSMjI2MyWTSu6aL5XnzxRVtO0n7ZuXOnG6tOGUJav23btrkpYylbR82kyVNPPWX/T/Pcc8+5UqnZt4n629/+5krGvPPOO5l1relvvPGGGzMVZQAAAAAAAAAAMFZdgji//fabK5lyQKEZKDhy5MgRhbuq9uFz++23u9LYPmnC/mruvffezGCQrFmzxpVq8/TTT7tSOq3/6dOn7TYsW7bMTR1L/Q15yT5zaqX+ecKm5/LeT1auXFkOfmkfqfk6AAAAAAAAAACQri5BnK+++sqVTG4AI1Znz551JWNuu+02V8rms39qoUBIUXz++eeuZMzChQtdKV8Y/Prmm29cCQAAAAAAAAAAJNUliHPLLbe4kjHnz593peahDJPdu3fbLJnOzk7T0tIyZgizbZLUpJl3ww03uNLk+SyWWqhJtx07dtj1b29vT92GyVLzc572R9p7JIdwv/3444+uBAAAAAAAAAAAkuoSxJk9e7YrlfqMaSZbt261TYNt3LjR7N+/PzdYU4vrr7/elbKFff7kCbNYsqiJMgVulixZYnp6euz6+ybPiiYMAgEAAAAAAAAAgEp1CeLMnz/flUqSHf+P1/Hjx12p9oDHRCiAs337djdmTFdXlxkYGDBDQ0PlYXh42PY3M54m0Kr5/vvvXWnyFMDxgSdl7nR3d5vBwcGKbVBgTdswlfQ+4XvUMqxevdr9NQAAAAAAAAAASKpLEGfBggU2m8WbTDaLMkvCv7/zzjtdaWqpCbUwgKPgzb59+2yTauqw3w+LFy92c9SmlibD9N5TQevrs24UwDlx4oTZuXOn7Ucn3AbVz1T75ZdfKt6jlqEe6wEAAAAAAAAAQCzqEsQRZbF4r7zyig3GTMSePXtcydjAkG7+18OxY8dcyZi2tjYbvMlT6/bU0mTYRPdN0gcffOBKpcyYvIDTVLxn2PdR2A8QAAAAAAAAAACYvLoFcdatW+dKxly8eNG88MILbqx2ylBRAMjbsGGDK03M119/7UpjXbp0yZWMefjhh10pndYrr5+ZsMm3s2fPulI6BVOmqs+aMJBy3333uVK6MGg1Ub///e9dqZRtNVXBKAAAAAAAAAAAUMcgjprK6uvrc2PG7Nq1y+zevduNVadAibJ5FAASZcds2bLFlkPXXHONK1X2nZOkAMOrr77qxvKFAZ00mzZtcqV0YYbKxx9/nBvcCDONptJvv/3mSmNpfaptQy1Ux6oXr9q26H3b29ttlpOafgMAAAAAAAAAANnqFsQRBV3Cm/wbN260He9/+eWXbspYutGvG/z6u7B/l7ffftuWk/7whz+4UikbJGvZygRSvy1ZbrjhBlcyZv/+/amBFx/80Pt0dHS4qWP7vVEfNL5PoLwsJK1rmGk0WWEfM//v//0/V6qk4JjqYO7cuRX9FqX1y6P97p08edKVKv397393JWN6enoy5xPtB9Wp9u8nn3zipgIAAAAAAAAAgDQtV0bZQkuLneBGp4wCH5s3b7Y37kMKINx7773mxhtvdFNKmTQKkIQ036FDh3L7d1m4cKEZGRmxZQUe1B/MXXfdZWbPnm0+++wz89Zbb9nXBwcHzapVq+x8CsIcOXLElkXruWjRoorMn2eeecZcf/31dvyjjz6y2UR63WcYKWghWtbevXvNvHnz7Lgo60hBK0/zPPjgg+bmm2+2QR8FMbQ8ra8yU1QWLTvMOFJQZPny5bacXOekcF5RJtPjjz9u94Myc/7zn/+U32doaMi89NJL5f3d29trtm3bZsuegj3+de0P38ycAl5hn0EKbPnlivb//fffb99XwjoQ1empU6cq9hdqV69jFdOLeo0XdRsn6jVe1G2cqNd4Ubfxom7jRL3Gi7qNF3ULNEbesVb3II6n7Brd7PdBkmp8MObPf/5z1Zv9ymhZsWJF7rJ9cMRvZ1pA5PDhw+UgTxYf7FDmSpjJ4oX7LxncSNI2vvvuu+arr74qB4QmE8SRrVu3mu3bt7uxsfSeO3fuLDdptnbtWvdKSfgeWfsjbT2qva+nYJACemHWEMaHL884Ua/xom7jRL3Gi7qNE/UaL+o2XtRtnKjXeFG38aJugcbIO9bq2pxaSEEDNWembBgFZ8Jm1jwFRfTawMCAOXfunA2W1JKtoSwdNdOlvw0DKwpYKBtFWSfJ/nQ+//xzV7pKzaANDw+PWY5fLy3HZ6soCKH1DOdLbpOCJfobrYPWxfPL0zrrPaeS1k/7OPmeWjcFoPSePotG/2taON/SpUtdqbQ/+vv7x2zj3Xff7cau0vsq00bLS+4H/b3WR/vr9OnTBHAAAAAAAAAAAKhBwzJxsoTZKgpsKPABIBtPQMSJeo0XdRsn6jVe1G2cqNd4Ubfxom7jRL3Gi7qNF3ULNEbesdawTJwsjzzyiCsZG8xR02gAAAAAAAAAAAAz3bQHcZYtW2b7WPHWr19v+5sBAAAAAAAAAACYyaa9OTVR9s2SJUvcWKkvGzWtds0117gpZkyfNsBMRRprnKjXeFG3caJe40Xdxol6jRd1Gy/qNk7Ua7yo23hRt0Bj5B1rhQjiyL59+2z/OBcvXnRTKnGiAEr48owT9Rov6jZO1Gu8qNs4Ua/xom7jRd3GiXqNF3UbL+oWaIy8Y23am1Pz1qxZY86cOWMzcFpbW93UUlZO2NwaAAAAAAAAAADATFCYTBwAteFYjRP1Gi/qNk7Ua7yo2zhRr/GibuNF3caJeo0XdRsv6hZojLxjrTCZOAAAAAAAAAAAALhqTCYOAAAAAAAAAAAAGotMHAAAAAAAAAAAgCZRzsQBAAAAAAAAAABAcZCJAwAAAAAAAAAAUEAEcQAAAAAAAAAAAArHmP8fKZnxEOO5MYgAAAAASUVORK5CYII=[/img]
– herr-fischer

2.

Terme addieren und subtrahieren

  • 1. Terme zusammenfassen
  • 2. Terme addieren und subtrahieren (verschiedene Variablen und höhere Potenzen)

2.1.

Terme zusammenfassen

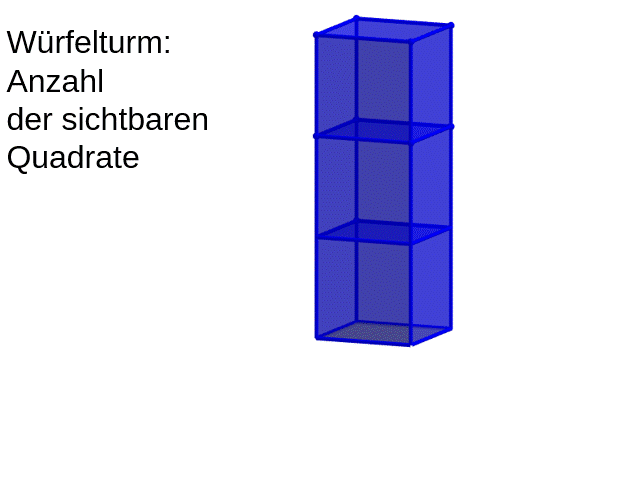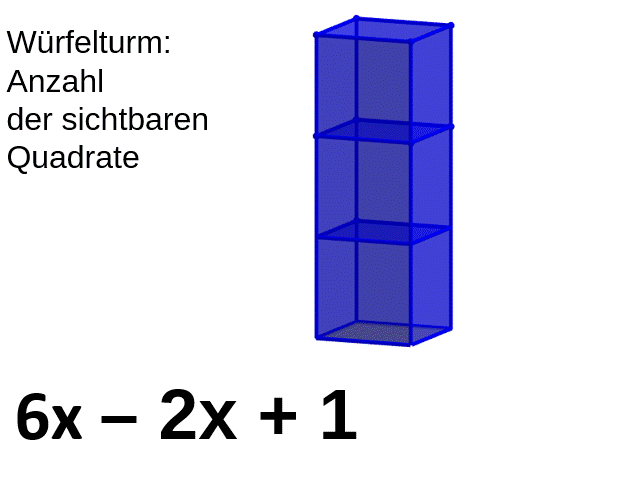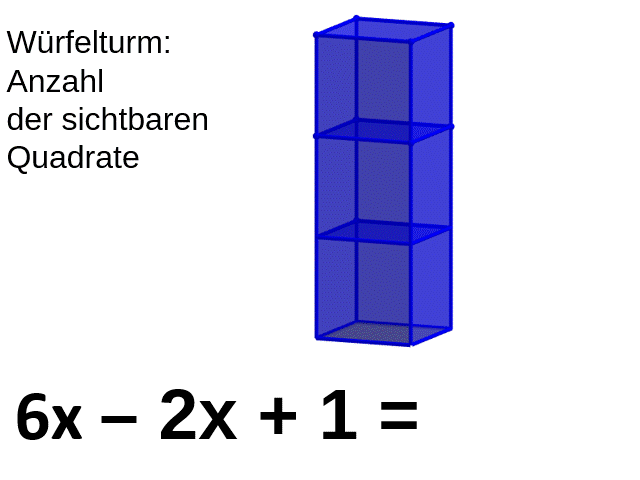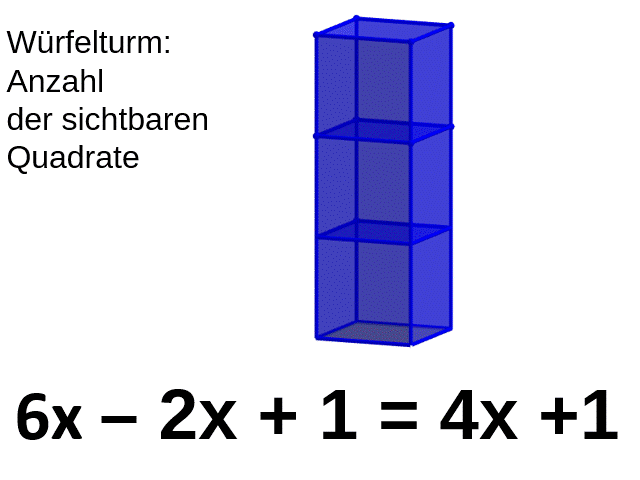
[br] [br] [br]Löse die Learning-App und übernimm den Text am Ende der LearningApp als Hefteintrag mit der Überschrift: [br][b][u]Terme zusammenfassen[/u][/b]
Übung:
Übernimm die Terme in dein Heft und vereinfache durch Zusammenfassen gleichartiger Terme. ([math]x,y,a\in\mathbb{Q}[/math])[br][br]a) 13x + 6 – 7x [br][br]b) 14a + 2 – 2a[br][br]c) –12x + 12 – 3x[br][br]d) 7 + 3y – 2y[br][br]e) 4x – x + 4 [br][br]f) 15a + 2 – 2a[br] [br]g) 4x – 3x + 5 – x
– herr-fischer

2.2.

–

3.

Terme multiplizieren

  • 1. Terme multiplizieren (verschiedene Variablen und höhere Potenzen)

3.1.

Terme multiplizieren (verschiedene Variablen und höhere Potenzen)

Terme multiplizieren beim Berechnen des Quadervolumens:
Aufgabe 1:
[b]a) Übernimm das Schrägbild des Quaders in dein Heft.[br]b) Erstelle einen Term (mit x) für das Volumen des Quaders ([/b][math]x\in\mathbb{Q}[/math][b]).[/b]
Aufgabe 2:
Aufgabe 3:
Übernimm die Terme in dein Heft und vereinfache. ([math]x,y,a,b\in \mathbb{Q}[/math])[br][br]a) [math]7x\cdot3xy[/math][br][br]b) [math]12ab^2\cdot\frac{1}{2}a[/math][br][br]c) [math]\left(2b\right)^2\cdot2b^2[/math][br][br]d) [math]3x^2\cdot\left(-2y\right)^3\cdot x^{-4}\cdot y^6\cdot\left(-a\right)[/math]
– herr-fischer

4.

Summenterme addieren und subtrahieren: Klammern auflösen

  • 1. Plusklammer und Minusklammer
  • 2. Zusammenfassende Übung: Terme darstellen, zusammenfassen, multiplizieren, Plus- und Minusklammer

4.1.

Plusklammer und Minusklammer

Beispiel 1:
[size=200][color=#0000ff][b]7 + (+3 – 8) = [/b][/color][/size][br][br]Welchen Rechenweg würdest du wählen?
[br] [br][b][size=100][size=150]Die Klammer in der Aufgabe heißt Plusklammer, weil vor der Klammer ein Plus steht![/size][/size][/b][br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAANAAAACvCAYAAACM0FBgAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAABVcSURBVHhe7Z1fbBtHfse/6pOgF3lNAWcUle5gOkiKUyM0YRKg1uUQAzHltM0fICmlA9I7wGkcurEfek6cKjGCwrlDqAR9cBqZairg0muPcpIiiQ+yYwVIcCZdRLnEpVoDtZtQyNlA4QeysvIg6G37oBnqtz/uLpfcXXJJ/j6DhYYzs/9m9rsz8/sNqT7TNE1EmD708aTIYSLSVdhTNPq8+G273+MJgiB4RwQkCD4QAQmCD0RAguADEZAg+EAEJAg+EAEJgg9EQILgAxGQIPhABCQIPhABCYIPGhJQoVBAX1+f721mZoYfunOYANAHYCeACs8Mn0qlgrm5OUxMTGDnzp3VOt25cycmJiYwNzeHSqUNFxYg586dw+HDh7Fnz57m7m9GtVEfgFWeGTBmA+TzeROA7y2TyfBDO4IohTy5j8x2eqvIZrOmYRg19ck3wzDMXC7Hd488xWLRTCQSNffDN8MwzMXFRb67aernpQwThiqfrGlFS/BLQ0foeQEl1T0YqpFUaAXT09M19QjATCaTZjKZrEkH0FEiKhaLNS8HwzCq9xePxz3dX7VVMqRsvqYlA2s7/0fwQKlUstx4qVTiRRzhN9y24ND7oAVVyF9ciUTC9g28uLhY86A1UtfthL8EstksL2Lm8/maHorfX7VVyqS9XHohv/g/ggfS6XT1ZlKpFM92hd9wTXB5sAMNuvcBTJSseV7Q+yaTSZ5VF/pwxeNxs1wu8yJVyuWy5U2eTqd5kchRLBa369ZBPJpyuWx5SUxPT1vyLS2TJm3m0Av5pSEjQjNUKhWcPn26+vnZZ5+15HcEKwAuqHgKwG6WHzIXLuiTA6+88gpisZglnxKLxZBOp6ufV1fDnkX757PPPqvG4/E4Dh06ZMmnxGIxPP3009XPX375pSXfwo9I/B9IPEBCF9D8/Hw1nkwmMT4+bsnvCN4h8UdJvAUUCgXL53vvvdfy2Y7BwcFqnIovqqyvr1fje/bsseTZMTo6ypPsGQcQV/Ez4VjkQhVQpVLBq6++Wv380ksvWfI7hu0OFKj//AbK+Pg41FAbpmli9+7Gur9kMsmTOp5vv/2WJzmTIvGPSTwgQhXQ/Pw81tbWAACJRKIze58VAFu3ACRaP3xrhsuXL1fjjQquHdAe5fPPP7fk2XHx4sVqvO79HSDxfyLxoOCToqDgk1k7k6MX+KSvJoRtRKDm0HRNrgmPE1F9jGaMCI3ALXb5fJ4XiST0WXFzc3BzN78/3jYwSfvB6n7w2nZu+D+CA5lMpnrR8XicZ3umpjJ4CFtA1PqWrck14bEK9THCFFAul/P8IEaNXC5nedAzmUyNtTGfz1sscHYWRt42MFkbMmucX/rMrcYNlEqlgttuu606fMvlcpicnOTFPNGHvq1h1HGeo6gA+ELF4wCc5qB3A/gZT/QA/ZWkvJqYMkxsVeHExATPqqIn84ZhuBoCPvroI57kCD0fNRYYhoHZ2dmm67xdLCwsYGpqypKm53Bff/01SqVSNT2dTmN2dpaU3ML2Z60Ok3lsBsDz21m67ZqGKyoIstlsVfGGYfDshoDJeplmNxdnmmMosWOw7l+H6rXyczaxNQLfF6q358OaTqJYLNY4g+lmGIarn4i3DUw2DE/Zt12z+D+CDbQC/A4jYLZRQPy8DqF6rfycTWyNwPelWzKZNIvFIt8lspTLZcflSnab0/3xtoEJE4tkX/Yc+MX/ERh0LGsYRs04tlFqKoOHMOdA9Njxmtxq8AJt+DAoFotmNpu1vLwMw7B9yKJGuVy2LNExDMPMZDKWay+Xy2Yul6spx++Ptw1M1o5RF1CQvY/pVCE0hCmgrHPF0+CFsAWkKZfLZiqVsjxkXl9i3ILnZ2tkGMmvl4uCQ5eG8fvjbQPTfSThl0D9QAsLC5aJ3sGDBy35Hce2g7xjiMViePPNN6uf19bW8N5771nKRInV1VWcOXOm+vns2bMYGxuzlOHMzs4iHt9aYrC2tmZZ7dJqAhUQXWmQTqdd12wJ4RGLxSwrED799FNLfpT4+OPt5QGGYXh2tqdS20sMPvnkE0teKwlMQLz3OXbsmCW/I9leUtY2JiYmfH+T99atWzzJFr5syM/mVQh0HZybeZ9D1/t5Wb1QJeCVTYEJiPc+dZdYdALf5wnthT5s3UhDQiDo4Zwj/84TgiMQARUKhe7rfTjNta1v9u3bV42fPn26/u8BKOjDePfdd1vyosTIyEg1vra25vnrF++++241XldAlB08wSfcqtAM9AtfQVuZaiwqrQz0W43MekNDmPAvm9ktX+HQZVRo0CLWasrlsuVaE4lEXashX/ZD11nytoGpnKe6fMDfJvZ9BG76DLqxaiqj1UH/OAVq11HpEDbUzAsXJ2KpVLKYeHXZqMMF7/SVdbv74+ssedvAhIkEacPFYNvO9xHC7H1MpwppZaBvr1xNrgn/VVgX7mjUW70f3fDyNo8K9Dmim9v92fmMeNvAZMds4uv4bvg6Qti9j+lUIa0M1Jnq4+sMfml0qUsqleoY8Wh4T+S2JZPJmh8UMe2eF+pETdTk8t0bxtcR6FuDd6VBwW+45YEuKHVYztNKSqWSmc1mzWQyafnqgn6opqena97KnUS5XK7eH+91vNwfbxvLQtLpmly+e8OE8nWGILFdnt5q7iFfmSgCYI5yE5Guwp6i5nkJue0CMWN3PT8lcfoDI0K04d8Vc18h1BQiIC88CMBQ8e1lW0LUoUsAnyPxABEBeSEG4AUVLwE4x/KFaKJ/RMQA8DjLCwgRkFcOkl7oFMsTokeBDN9eUC/BEBABeYX2QhdUAwnR5RX111Avv5AQATUC7YV0AwnRo0B+ijnE3gcAxIzdKAWyuvfgVuP4NYUKwdGHvq056hWVQH6Bxw6/bScCCgC/jSAER6PPi9+2kyGcIPhABCQIPoj8EE4Qooz0QILgAxGQIPhABCQIPhABCYIPRECC4IOeFdCJ3BJPEjqI9Y1NzC0tY+aD3/CsltKTAtKV/1jmn3mWEHEuXf0GJ3JLSDz3RiRegj0poG83NgEAl67+Dvtefgs3yt5++lZoD+sbm1gorGDfy2/hscwvMbe0jHXVhnvv+C4v3lJ60pF65fpN7Hv5rernwYF+vH/8SYyO7LKUE9rLpavf4KP/+B8sFFaqgqEMDvTjqzdD+qqpR3qyB+KNsb6xiX0vv4Xzl69Z0oX2MjjQ7ygeAPiTNvc+6FUBOfHjN95p+6RU2GZ0ZBe+eO2I48jg+8Pf4UktpycFdKPs/F8OXv/wIo7On+XJQpsYHOjHyakHeTIAYGo8hJ/ZaZCeFJATe+/4Lt4+8hc4ObWfZwlt4kb5Fo7O/xoAMDy0/a8Vhod2WD63i54UkN2YenRkF94//pc4cNftGBzo59lCG1jf2MSP33gXN8q3cOCu2/HJ3/0Vjj1yPwBgdKT9wzf0soCGh3bg5NR+fPnaEUBZ5sScHR3WNzZxdP4srly/idGRXTh18GEMDvTj+Ud/iFMHH8aBP76d79IWetaMPTy0o9rTnMgtYW5pGZPjYzh18GFeXGgDR+fPYqGwguGhHfjg+JORGK7Z0ZM90OjILsswTQ8Lzl++Jr1QBJhbWsZCYQWDA/14+8gTkRUPelVAnMGBfkyOj2F9YxPnxBfUVuaWlnEit4TBgX6cOviwowk7KoiAFKm9dwLKjC20h4XCSrX+T07tx4G7ojHPcUMEpNh7x/cwPLSjuu5KaC1Xrt/EidwS1jc2cWj/fZiMgI/HCyIgwnNqLvSPH7fpX3L3KDfKt/BY5pdV8XSSH04ERNA+IDFptw7t61nf2MTk+FjVoNMpiIAI2pgAAK/JXCh0uK/n5NT+jnNii4AY+g24UFiRXihkTuSWcP7yNQwP7cDbR57oOPFABFQL7YXEpB0eJ3JLHePrcUMEZIOYtMNlbmkZc0vLHePrcUMEZIOYtMOjE309boiAHBCTdvB0qq/HDRGQA2LSDpZO9vW4IQJyQEzawdHpvh43REAuiEnbP93g63FDBOSCmLT90w2+HjdEQHUQk3bzdIuvxw0RUB3EpN0c3eTrcUME5AExaTdGt/l63BABeeDAXbdjeGiHmLQ9QH09xx65vyt8PW6IgDwwONCPh9RbVEzazly5ftPi63n+0R/yIl2HCMgjYtJ2Z8tc/euu9PW4IQLyCDVp58SYYKHbfT1uiIAa4OkH7wUAvCXGBAtH589WfT3vH3+yZ8QDEVBjjI7sEpM2QztKta+nl8QDEVDjaJO2GBN6x9fjhgioQbRJ+0b5Vk8bE3rJ1+OGCKhBxKRt9fWcnNrf9b4eN0RATdDLJm3u6zm0/z5epKcQATVBr5q0e9XX44YIqEl6zaTdy74eN0RATdJLJm0tnvOXr6n/5Ndbvh43REA+6BWT9usfXqz6ek4d/HMRD0EE5ANq0r5y/SbP7grE1+OOCMgH1KTdjd8VWiis4ERuCQC2/i9pj/p63BAB+aRbTdra14Med5TWQwTkk240aYuvxzsioADoJpP2ehf/hlsYiIACoFtM2usbm/jJG+/gRvmW+Ho8IgIKiE43aWtfz6WrvxNfTwOIgAJicnyso03a4utpDhFQgHSqSVt8Pc0jAgqQTjRpzy0t40RuqSoeMVc3hggoQKhJuxN6oSvXb1a/FHfskftFPE0gAgoYbdKOujVOfD3BIAIKmE4wad8o3xJfT0CIgEIgyiZtba4WX08wiIBCIKombfH1BI8IKCSiaNKmvp5e/A23MBABhUTUTNrc19ON/+yqHYiAQiJKJm3x9YSHCChEtDGhnda4S1e/EV9PiIiAQmR4aEdbTdpXrt/ET5S5Wnw94SACCpl2mbSpr+fQ/vtwcmo/LyIEgAgoZKhJ+9LVb3h2KHBfjzhKw0ME1AJSe+8EAJy59J88K3DE19NaREAtQM89WmHS7vX/19NqREAtgJq0w5wLzS0tY6GwgsGBfvziyBPi62kBIqAWoY0J5y9f41mBwH09e+/4Hi8ihIAIqEUMD+3A6MiuUEza5y9fE19PmxABtRD9XSH9g4VBcOX6TRydPyu+njYhAmoh2qS9vrEZiElbfD3tRwTUYoIyaa+rH0AUX097EQG1mCBM2trXo//Zlfh62kefaZomTxTCZW5pGaMj38HoyK6mHvyZD36D1z+8iOGhHfjg+JNirm4jIqAO5ej8WaT23inm6jYjAhIEH8gcSBB8IAISBB+IgATBByIgQfCBCEgQfODZCteHPp4kCD2FiVqpSA8kCD4QAQmCD0RAguADEZAg+EAEJAg+EAEJgg9EQILgAxGQIPhABCQIPmhOQH0etj0AJgEs8J0JuuwEz4goM+SaCzzTAxNkf6EraE5AXigBOANgCsA9AIL9KTRBiAT+BZRx2FKkzBcAHgBQIWmC0A2YHgENIJtbKMFEgpRNs3ydnqzZM5ohQ645X5NbPyQ91puESAY7/PdAbuxWwzjNaemFhO4iXAFBiShBPv83idejQCbdMzyT4bXsKoAX1byMGj0mAMwFIPAKO7abEcWNirqeCQA7yfF2ejDOgBk8NAW1Lz3eBIBzpAzUuWfYfewBcLhO/bTjnBpaX3p/fa4ZD8fQ+2mDlr6ePSrdyWjEuyQnLJ2Z1yGcDnToQoc+9YZweVImU5PbeNkcu3a7zYCJYs2eW6HeEK7Mhqw5lu91CFeEibjNtfEtqc5pF+i1FmFi2mZ/umXVfnlVBzxfb/GIndP0WF9u7WqStkk6HC9vL5Xwe6CosKosggBgAMgBKKrqySvDBwCs+TB4TCiDCQBk1Zu3USrq/CX1OaWuzwRQBrBIevQLAP6e7OvEUwB+DiAOYFodY5EZep5Rb9wfqDpIq3vIq7+GKlcCcILs50SrzrnK6mta7a+3jDqOblcv1uCn1PEMdb0ZAL/PCym4opywqJUqs14osfL0TaLTWtED0bfjYk3uVsiSMvrtSINbD5QmedxYooOXHohew3RN7lYoszekXaDXqq/J7i2eYuWc3tRFVsYutOOctN55j68DPY7Ts0bbBupe2LXbEW4PtMreOCkAMfK5XdzBExSPk/inJF6Pw8pAAvUWnWX5jUDP+zckTomxenUan2v0NdnV/bMkbqgedOuf6VkZA5BU8TXVtm604pyrrN6devwxlQ/Va/PjcLIAnne4doZ/Ac04bJOq+9ZDGkN16VHgdZ6giJGu/295pgMzpBFTPsUDVWdJtbk14CBPcOFHPIHwhyR+rzL6OLGPxP+XxO1oxTk/J/E/I3E76PV8TOJ2HOIJzvgX0HGHjZqvE+rN6lZRYfM4GVOfVtaVF23e3uNqs3sjchbUvULd45ssvxl+BuAjtbUCN5GGRVDn/C8Sb+T/iq3zhObxLyAn9AQsB+C3Hh/IMNkN4F/YxPTnagLbR0zDXo0HvyJGiYR64IN6MKCuY0GJfMLG7K6F28t8SeJDrH749gNSNkD8C8g69dre/k89AE7j0nbwEICvlFUlzvL0ur3bbHwUdtQbR/thRl3HlBL5BTUUTpDhHb9+oS34F1CnEVMTxK9VL5RTPaXumdYA/KkHEb1EJqZfqF7Ca+/lxmHVu6wpkWSJuf23ZHj3NN+xx+EvcLfteb5z8/SegCi7ydBN90yaoyTuxCyxEn0B4K9ZfqOsEINEAsCymtC2e/gbVe4mcS/+nRDoHAH5nfhp66BTz6J7Ju2k1I65evwr2eeM6kGa5QKJ/zTgOVU38kckXm+JmF6a4/YMNEG0BUS9v3TCaMeveAJDWwdP8QxGow9tTA2p9JzktFqT5Zc/4AmECoB3eWIP8iCJ/4LE7Vgmz8AVntk87RWQnndQez5lNylzwaGbXlXzDz30cUI7Hp2OA/Vgfq3ijUzSYwD+jVzrMw6LPem/MrW7hhESd3ohVNiSoV4mxhykbi8u+uLUw+4AaK+A9qu/a2ouUrB5sF4g8QfUEIk7ay+wFd92UO/3A2p/fa6K6tYnyNCt0Un6GFtFMGXjY3qAxJ9S56RlHmS+qhmVr7cXlXVOW+QE4CSpi2fUM6HrtaBeZPeQ4XEq4DklX9vjhGVVELVp+Al0jZLe+FolvsLZbst4WAtnelyNDZe1bG5r4XSg5+BrvPgaNr3RsGiTTzdDlaH3a3ctXq5VB12O1z0P9Y5ZL5+GoM5penxGoNbg2a3NM72tU7SjvT3QmDLRUjMyR88xuO8mrrrvopr8O62WpUyqHmbaphtPqOPlfS7HmVSmZ9is7I6psXjaZYj4kLqnNKuTpDruV6qMsE1Mmfi5SwKqnvWK9oUm5rh1kP8PJAgeMVErlfb2QILQ4YiABMEHIiBB8IEISBB88P8VEXrmnMD7mwAAAABJRU5ErkJggg==[/img][br][br][b][size=150]Die Plusklammer wird weggelassen. Die Zeichen in der Klammer bleiben gleich.[br][br][/size][/b]Rechenweg 1 ist also richtig: 7 [b]+ ([/b][color=#ff00ff]+3 – 8[/color][b])[/b] = 7 [color=#ff00ff]+ 3 – 8[/color] = 10 – 8 = 2[br][br]Rechenweg 2 ist ebenfalls richtig: 7 + (+3 – 8) = 7 [b]+ ([/b][color=#ff00ff]–5[/color][b]) [/b]= 7 [color=#ff00ff]– 5[/color] = 2[br] [br] [br] [br] [br] [br]
Beispiel 2:
[size=200][color=#0000ff][b]12 [b]–[/b] (+2 – 5) = [/b][/color][/size][br][br]Welchen Rechenweg würdest du wählen?
[br] [br][b][size=100][size=150]Die Klammer in der Aufgabe heißt Minusklammer, weil vor der Klammer ein Minus steht![/size][/size][/b][br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAOkAAAC6CAYAAABLLWq6AAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAABZeSURBVHhe7Z1fbBtHfse/6pMgoJFoCTgjqHSGqSIJapxSl74AsZJDAtiUfWlyeXAp5ZreAW7jUoH90Etkh64RFLqkkJMnBxeLlxNwybUllRRI4oNsRwESXEgHUKK6ZOvg7Fo0fDJQ+IGqrAQQ9LZ98Cyz/PG33F3+He7+PsDA3t8Ol7sz+52Zne8s1WUYhgFBELTlj2hAEAS9EJEKguaISAVBc0SkgqA5Xb6aOOrqohE98FERdzxe7xEN6k56UkHQHBGpIGiOiFQQNEdEKgiaIyIVBM0RkQqC5ohIBUFzRKSCoDkiUkHQHBGpIGiOiFQQNMeVSNfW1rBt2zZ0dXWVpWw2S7M6kk6nMT4+juHh4bJjjY2N4eTJk8jn8/QjHcN5AF2WtA3AGs3UArLZLCYnJ7Fnz56yMt6zZw8mJydx/vx5+hHtofee2zQ2NkYPhUlST5U5NMNwoFgsGpFIxABQkTKZDM1uSyaTMcLhcMUxuBSLxYxisUgP4czd5dBtS2FyHQlzX4soFApGNBqtKE8uRSIRI5fL0UNoCz1/tykajdIDGQUmX4apz1bWXTWqnkUmkzFCoVDFBZUuzKVIU6lUxWedUiQS8S5UWsAtTCnmGgrm/haQy+Wq1hWXQqFQxwiVnrvbxInUAIw4zcfUaavqzgn2LAqFghGPxysumCY3Ii0UCp5vHjPFYjF6uOrQAm5hor1ozLq/BdiNdpxSOBz23hi2mFwuV3HebpOdSHNMXrY31YCy90lPnz6N9957D8vLy+VjYhsymQxGR0dpuIzJyUmcPXuWhhEOhxGLxdDb24vLly9jfn6eZgEA5HI5jIyM0DCP13cFG0QWwCMktgDgoLnxbRGzZLNZPPJI+RG8vOabTqcxMTFBwwiFQhgfH8eOHTtw8+ZNpNNprK+v02yYnZ3FkSNHaFgbuPKJx+PYsWNHWYxjaGgI4+Pj3wYs98geANY7PQrgomUbcK67lmBVLG1ZnJKbnpTrRePxOM1mOySemZmhWe2hrWCLUoycc4jmcSCTyVRctxdisVjF57nHBbshcUVvoxlc+bi591gs9TJLjgnrI4rLumsFrkRqN/R1KiiucEOhUMXNY8IN2TzdQLSAW5CKTLnEaT4HuHLyAv0sqtRNIpGoyOv1+1oN14DbXZ8jlnrhJpBKk30u664VVLVgQqEQFhYW8Mwzz9Bdrvjqq69oCOPj4+jv76dhAMChQ4doSHs+pgEAj9JAE+Esq3A4bPsYcuDAARrSntXVVRrCAw88QEOe2QkgQmL8Q1d7YUUaDocxMzOD69ev4+DB0pOVZzY2NmjI1XNEJ/EBDQDYRwNN5JtvvqEhDA8P05DvsGvovbKfbBcAVDZ77aVMpKlUCoVCASsrK5iamqq7IKampqCG1KU0NTVFs5X45JNPaAg7d+6kIa1YJNthAPWVmjdGR0cryvjixYrpjxKff/45DSEcDtOQVnCN/draGpLJZMWCDa+LYvbSAICPaKDd0PEvB/fMVNdzAUOhUKg4PgAjlUrRrPbQ54kmJ24av8x6MZMDXPk2C25BCTeRpxPcAg1u/oImdlEMqRvuubTV9pkT7HC3HSQSCRpCKBTCvn2tHDx64/c0AGA3DSiy2WzFkjUzUXsBDsvgaiWZTKJQKNBwzXMO7cSNTTg/P4+xsTGsrdkvzuTGac5Hbi1aiDSdTrM+6YkTJ+oecjeTyukMYBcNaEI+n8dLL71Ew4hGo7aTTH5geXkZzz//PA2XESXblc1Ym6FdKwc3HEODhrvc9Dq8Wi8mdJjZ5ESXlqHKqhW7MqwlecXOH61mh+kEPW+o+2NhYcEoFAqGocp3ZmamIp+ZSssfad2oJYEV+S11125cnYXdDVavSO0EyhnxbqDHqTXNMBXJpaqVa01VyrCW5IVqAq1l3S73fFhL8tIIZzKZimSHXTmXFsXQumEWo8Da2GqAq7Owu/BqheWEnaleq0ANTURK87ipaK58G0EqlWqoQI02idQr3Aqs0vfRulH1TfPrJNK2PJNOTk7i1VdfpWFEIhFcvHhR6+fQTsFcz0vX6oZCIXz66afu10N3ILt3203fdSYtFena2prtgvtoNCoCbRDJZJJdcB8Oh30v0Fq4SQOa4eqvqnFvIcDlWzAma2trGBsbY6fO4/E43nzzTRr2zOk67AkrDwNwc1VjjPHNFqZDEXPl66JaWOwawUaNUtLpNLtMzysVb6fYwFlOTvfdyZMnK0ZqZifAvSnF1WPGvAdqrIeGQse/HNwzEzw8k1b7dYdEIkGz1w7zvNHMxD2T2k0cVYMr31qwexEiGo3W/Jzfbrj7xunNqKoLNmjd2NRjK1/Yd8LVWXA3EVyKNJfLsQUNr6uJ3MBUQDNTgrkmOwumGlz5eqFYLLKTJeiA1UROcA1PtYmv2dnZivyw3mu0bpgX9uGh7lpBU4e7+Xwejz32WMXkBdTwy+1bLw8//HDV7ynBDGWayWkAx0ms7GVvE4ci5srXRbUADo8RoVAIJ06coGEWt8PPVsOVjUk8HscTTzyBe+65B19//TXeeecddlFMOBzGysrK3Q3mHqGRMACV27HuWgJVLQfX0sNFT8pN/9eSnIY3JZhWspkpw50rk8+JYrHo2gek2PWgXlMzLZF64XpTL2lhYeHbg5G6cVx/rQFNnd3lelA/wb3RWPkejzP9/f0YHR0tS265c+cODfmO6elpRCL0zU93pFKpqq9bell/3S6aKlK/08+8NPwF2Rbqp7+/H19++SVmZmYQCoXobpZwOIyFhQXHIfx/0wCzlrfdiEjrhL40vK7hS8N+YWpqCtevX0cqlUIsFqt4DzYSiSAejyOVSmFlZaVqD2pC3wcOAdDNRXY1cdQxMJMCzSYP4EESSwB4xRrwURF3PJZ75IaaJLISB1Dm2GtQd9KT1skIM+StnF8UdIT7fSod36wVkTaAn5FtHX8nR6jkV2Q77HKlWasRkTaAcWbY9C7ZFvTiBvMLDD8n27ogIm0Qz5Hts236i2qCO+bIdlg1tjoiIm0Qh9XMoMm6zTOP0H7WVCNqRddeFCLSxtEPgC7A+0eyLejBnGpETXTuRSEWTOOhf1b5AQD9PirijqerC3kA1p8Uv9fmVwMBPSwYEWkr8FERdzxe7xEN6k6Gu4KgOSJSQdAcfw13BcGHSE8qCJojIhUEzRGRCoLmiEgFQXNEpIKgOb4T6akUfdde6CQ2NreQXFzC6Q9+R3cFFl+J1Kzgp2feobsEzbl09SZOpRYRefENaWgJvhLp15tbAIBLV/+Ax19+C7eK/v8lvU5mY3ML6Wwej7/8Fp6e+Q2Si0vYUHW49/7v0uyBxVeLGa6s3sbjL79V2u7t6cb7x5/FrqHtZfmE9nLp6k1c/M//QTqbL4nSSm9PN67/4kUaDiy+6klphW9sbuHxl9/ChcvXyuJCe+nt6bYVKAA8LL1oGb4SqR0/eeNdmYjQiF1D27H82lHbEc6fDX6HhgKNr0R6q7hBQyVe//AzHJs7R8NCm+jt6cb0xD4aBgBMjOr2y7ftxVcitWPv/d/F20f/CtMT9KeshXZxq3gHx+Z+CwAYHOgrxQcH+sq2BZ+JlHvG2TW0He8f/xsc2H0fenu66W6hDWxsbuEnb7yHW8U7OLD7PnzyT3+HF556FACwa0iGuhTfiXRwoA/TE/vxH68dBdSMr1gx+rCxuYVjc+dwZfU2dg1tx5nDT6K3pxtTP/oBzhx+Egf+/D76kcDjOwtmcKCv1GOeSi0iubiE8dERnDn8JM0utIFjc+eQzuYxONCHD44/K0NbF/iqJ901tL1sSGsOoS5cvia9qQYkF5eQzubR29ONt48eEoG6xFcipfT2dGN8dAQbm1s4L15pW0kuLuFUahG9Pd04c/hJW/tFqMTXIgWA2N7vAcqCEdpDOpsvlf/0xH4c2C3PnV7wvUj33r8DgwN9pXWiQmu5snobp1KL2NjcwpH9D2FcPFDP+F6kAPCiejb95cfyd7hbya3iHTw985uSQMWnro1AiNT0SMWOaR2mF7qxuYXx0ZHSJJ7gnUCI1JxAAoDX5Nm06VAvdHpivywkqYNAiBQWOyadzUtv2mROpRZx4fI1DA704e2jh0SgdRIYkVp7U7Fjmsep1KJ4oQ0mMCKF2DFNJ7m4hOTiknihDSZQIhU7pnmIF9o8AiVSiB3TFMQLbS6BE6nYMY1FvNDmEziRih3TOMQLbQ2BEynEjmkI4oW2jkCKVOyY+hEvtHUEUqQQO6YuxAttLYEVqdgxtSFeaOsJrEghdoxnxAttD4EW6YHd92FwoE/sGBdYvdAXnnpUvNAWEmiR9vZ046DqDcSOsefK6u0yL3TqRz+gWYQmEmiRQuwYR+5aLb8VL7SNBF6kVjsmJRNIZYgXqgeBFykAPLfv+wCAt2QCqYxjc+dKXuj7x58VgbYJEan6vV6xY8oxFyuYXqgItH2ISBWmHSMTSOKF6oaIVGHaMbeKdwI9gSReqH6ISBVix5R7odMT+8UL1QQRqYUg2zHUCz2y/yGaRWgTIlILQbVjxAvVGxEpIWh2jHih+iMiJQTJjjEFeuHyNfUX0cUL1RERKUNQ7JjXP/ys5IWeOfyXIlBNEZEyWO2YK6u36W5fIF5o5yAiZbDaMX581zSdzeNUahEAcObwk+KFao6I1Aa/2jGmFwpZrNAxiEht8KMdI15oZyIirYKf7JgN+Y3cjkVEWgW/2DEbm1v46Rvv4lbxjnihHYiI1IFOt2NML/TS1T+IF9qhiEgdGB8d6Wg7RrzQzkdE6oJOtWPEC/UHIlIXdKIdk1xcwqnUYkmgYrV0LiJSF1jtmE7oTa+s3i69uP3CU4+KQDscEalLTDtG91le8UL9h4jUJZ1gx9wq3hEv1IeISD2gsx1jWi3ihfoPEakHdLVjxAv1NyJSj+hox1i9UPmNXP8hIvWIbnYM9ULlD/r6DxGpR3SyY8QLDQYi0howJ5DaOct76epN8UIDgoi0BgYH+tpqx1xZvY2fKqtFvFD/IyKtkXbZMVYv9Mj+hzA9sZ9mEXyGiLRGrHbMpas36e6mQL1QWawQDESkdRDb+z0AwPyl/6K7Go54ocFFRFoH5rNgK+wY+XuhwUVEWgdWO6aZz6bJxSWks3n09nTj10cPiRcaMESkdWJOIF24fI3uagjUC917/w6aRfA5ItI6GRzow66h7U2xYy5cviZeqCAibQTmu6bmj043giurt3Fs7px4oYKItBGYdszG5lZD7BjxQgUrItIG0Sg7ZkP9iLV4oYKJiLRBNMKOMb1Q8w/6ihcqAECXYRgGDQq1kVxcwq6h72DX0PaaxHX6g9/h9Q8/w+BAHz44/qxYLQIgItWPY3PnENv7PbFahBIiUkHQHHkmFQTNEZEKguaISAVBc0SkgqA5IlJB0JwuA5DZXUHQFcOQnlQQdEdEKgiaIyIVBM0RkQqC5ohIBUFzRKSCoDkiUkHQHBGpIGhOWxcz5AF8A+BeADvpTkEQyhczZAF0Mel8+UeqYneMLM0IYBLAgwAeARD2+D1+gpbVaZrBBVy5C/7Bcbh7DMAaDdrwcxqw4QaAsyR2hmwLgnAXR5EWAMzRIEMawEc0aEMvDQCQX/MRBB5HkQLAcdX72bGmhq9u6QeQAhBS21EAL5E8giDcxZVI4SDCOQDrNOjAOID/w91Zq4sA7v7ZI0EQKK5F+pHN5M4N1dMKgtAcqoo0Qra5SSTawybIth10NpKb1RyzybOm/r/Hsm9YnYvdsNzLDOhpD3lvADjJnOs2FUsyZVYLk8zx6/3zUGk1ohkmxx52ee60jMxZ/BvqfK3HHVblSo9nnsM2S95xmw7BpF3fayWvvst6D3ap7ZNV7kMTu2s4b7mXxszMBmAYgJG5O/IsSwuAESKxGZXfUPut+6I2x8lYPmMmmsd6XDNFmePnmHOyppDKQ4/FnRfNY6YZl3m5fFyyOyeDycuVwyyTL2XZ7+XaDHUuEeYzXAp7PPcUE7emCGAUAaPA1C9N1mvU4XsNdYw48xkuJZjP213DAnPcKGAYhmHA/BBX0Rmbiy+oz4RJPFflOE4nyd2ctDDDDgI1U4Q5FndeNI+ZOPHRPFy5VEshS7lZE81Hy4H7HnoTebk2g6k3pxRmjmEw+dwKP+6yHuGyzFr1vQZzTzqlOHMMt9dgirTqcBdqCBAlsUk1hChYYokWTP4U1ARVCEAcwIz6l7LcgKGgE78m2xF1fmYJZ9QiDZN1AP9u2XaDOaSyEld1UitpUm8AMAugqM67qLatFFwOA5fVv2F1P8ww9w6UR25ONEZUvoRltt+KmzJr1fcmGZsxASCnyi6njmnlrMeyg7qOKIC/MAOmsrnW2OwBc8w+a4sUUsMAp+NUa0loD2LYtFrmsMWajxsOzpI83HnR7zOTm56UnhvXYtLjxJg89HvMcigwrT73HUad12Z3TNqyc/VDv9PueDEmX4i5L4rMNUeZ49Fjtep76QiEKxODuR+5kR09L6jzrejB3Qx3zf0JZr+ZrIJwOo7dSXIXTIUQZgTq9njcedFjmIneyFxeem5QsRRX0FUSPcaMukYqEq5xMpOXayuo/GayO1d6fbQ8DeY7uUbIYOYuYHNPcN/LiYUeqxXfy3VUdvVRZPLScqb77a7B1XDX5B9shgVhAEdosEkMq4UQOnCMBtRQaEKVyTY1LE3TTC74MRn+RJSX3Ihr3wlgVKU/BvCFenQZV7OJZvqCftAFu2lAcQ8NNJhWfO/vaUDVk7XMzPRjmhHA/9IAwe4a4GTBWOkH8CYNMs9mQeEg8/xhZR3AvBLtNpfPJQDwS+a5528bJFCT86rBe1Cd33F1rh9ZktfFKX5nlQZIedHUSFyLFMwkUky1yEFlSk2qJMgkEWUdwA9d9qrPMZMeLzVwIuykOhc6eWROVpgTctWuR2gtnkQKNewyB9Jubjq/sxPAKwBW1OzerGq8uEcDOlNrx7+Sz6+r3pQa8l65AeBVEospwa6oun1TNT7DJF/QGaIB+lDpkOrpzDyL1E9w77kCwAYNuGREPZ+nAVxn7KF1lz1iP4BPSWwZwPMkVg1O0B/TAIBfyAv3rniABhzqMksSVx9uCbRIL5Bt820e2ttQ1phlXbQS+gE8Q2JeGGH8ynmb5ZMcSzRg0/hwz7rnm/Bc1emMMI8A/0y2TfLqxwysiZt4cktgRMoNN15Vay3N2c0/ZV5G5+hnhrPPk5Z1DcC/WbahPuNlwccRpjc+zkxC3Uu2oWafTxNRc0O2SUsDYy6e+CHJI9yF/qjBvJrNPW/pMZMAHiP5Qjb3n1sCI1IwNzzUMNKc3bSuRnGCtqLzarbU7FkHGMGfINtumGbO569Jg7CTyVNQ12V9Q2kf07icVefapc7fPGeaT7jbkNN76CPVqJk95t8zM+OcK+KFQImUu+EpKQA/o0GGIw4WDCWhJmS80g/gVy4mkmgejn4A/+KQL6TK4Pt0hwAowbl908ssy3qWcSJoIu1XM5jUMgmrFrKgCvRPLPuqYbVgoszNH1X7CmoGuFZGlLis0ImkERVLODREB1W+OCmDiPrssiqDxy37hHJeIfVuJaRis5ayrJe2/qSnIAgOyN8nFQT9EZEKguaISAVBc0SkgqA5IlJB0BwRqSBojohUEDRHRCoImiMiFQTN6TIMQ1YcCYLG/D96Zcy9ksFLDAAAAABJRU5ErkJggg==[/img][br][br][b][size=150]Die Minusklammer wird weggelassen. Die Zeichen in der Klammer werden umgekehrt.[br][br][/size][/b]Rechenweg 1 ist also richtig: 12 [b]– ([/b][color=#ff7700]+2 – 5[/color][b])[/b] = 12 [color=#ff7700]– 2 + 5[/color] = 10 + 5 = 15[br][br]Rechenweg 2 ist ebenfalls richtig: 12 – (+2 – 5) = 12 [b]– ([/b][color=#ff7700]–3[/color][b])[/b] = 12 [color=#ff7700]+ 3[/color] = 15[br] [br] [br] [br] [br] [br]
Übung:
Löse die Klammern auf und fasse zusammen.[br][br]a) 23 + (+7 – 11) [br][br]b) 6 – (–8 + 2)[br][br]c) 10 + (3 – 7)[br][br]d) –5 – (8 – 2)[br][br]e) 2 + (5 + x)[br][br]f) 15 – (–6 – x)[br][br]g) 7x – (9y + 3x)[br][br]h) 8x + (–2x + y)
– herr-fischer

4.2.

–

5.

Ausmultiplizieren und Ausklammern

  • 1. Ausmultiplizieren
  • 2. Ausklammern

5.1.

Ausmultiplizieren

x-beliebige 10er-Stelle:
[size=150] [br]Die 10er-Stelle soll nun eine [color=#0000ff]x-beliebige Zahl[/color] sein. ([math]x\in\mathbb{N}; x<10[/math])[br] [br][br]Wir können den Term dann so schreiben: [/size] [size=200][b]7 · ([color=#0000ff]x[/color]+[color=#ff0000]3[/color])[br][/b][/size] [br] [br]Notiere die richtige Termumformung im Heft: [b]7 · (x + 3) = ...[/b]
Übung
Multipliziere aus. ([math]x\in\mathbb{Q}[/math])[br][br]a) 5 · (x + 6) =[br][br]b) 15 · (2 + x) =[br][br]c) x · (8 + x) =[br][br]d) 9 · (x – 6) =[br][br]e) –2 · (4 – x) =
– herr-fischer

5.2.

–

Information