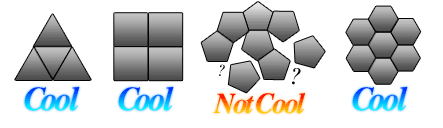
Consider an infinite plane, and how you might be able to cover the entire surface with shapes, which is to say no gaps or overlapping between. We will call this a tiling. As you might expect there are a number of different ways in which you could do this. However, if you are able to do it with a single shape section, and only by translating that shape section within the plane, we call this a periodic tiling.

Periodic tilings also exhibit rotational symmetry. For example, a rhombus pattern has two fold symmetry, because rotating the tiling 180 degrees in either direction, the tiling remains the same. Likewise, equilateral triangles have a 3-fold symmetry, squares have a 4 fold, and hexagons have a 6-fold symmetry. However, there does not exist a 5-fold symmetry with regular pentagons.

"5 is interesting because it is not 3, 4, or 6"[br]-John Hunton, Mathematician

In 1619, Johannes Kepler was the first to propose a tiling with 5-fold symmetry, although his pattern's rotational symmetry did not line up exactly, nor was it clear how to extend the pattern periodically throughout the plane.

In general, there are an infinite number of tiles that can tile the plane periodically or non-periodically. For example, consider a tiling made of a "sphinx" tile. You can form the general shape of the sphinx with smaller sphinxes a number of different ways, hence, filing the tiling with a big sphinx in one orientation creates a periodic tiling, but changing a single one or a few within that tiling forms a non-periodic tiling.

However, in the case of certain regular polygon tilings, you can only tile the plane periodically, such as with regular hexagons.

This raises the question of if there are shapes that can only tile the plane non-periodically. In the 60's mathematicians started to develop sets of tilings that could, gradually getting to less and less tiles. However, it took until 1974 when Roger Penrose got it down to 2.

Penrose developed hit tilings by connecting 5 pentagons around a center pentagon, and observing that this pattern fell within a pentagon itself.

Inscribing this same pattern within the pentagons contained within it, then the gaps start to connect up into distinct tiles.

Continuing this process with remaining pentagons we reach a point of totally distinct tiles including stars, rhombuses, pentagons and justice caps. Continuing to subdivide after this point, only leads to these tiles emerging.

This pattern, when extended out to the infinite plane can only tile it Aperiodically. Interestingly enough, if you overlay Kepler's attempt at forming a 5-fold symmetric pattern on Penrose's they line up!

Decomposing the four tiles that emerge into two rhombuses we finally have an exclusively aperiodical tiling of just two tiles.

While Penrose initially discovered his tiling by dissecting pentagon patterns, there are other ways to construct a Penrose Tiling, in particular by using parallel lines. As you might be able to see with other, periodic tilings, we can abstract them into sets or rotated parallel lines. In the case of an aperiodic tiling, we can begin by construction a grid of parallel lines offset with a 5-fold symmetry, which is to say 72 degrees around from one another.

Already, we can see the aperiodicity of the intersections between the lines. But! If we take each intersection between two lines and draw a tile, with faces perpendicular to the lines involved, we find that not only do the same two tiles emerge, but they connect together to form a Penrose tiling!

Following this process, we know that adjacent tiles long a single line's sides will both be in the same orientation -- perpendicular to that line. Thus they line up. Continuing for all the intersections in the pentagrid, forms a complete aperiodic Penrose tiling.

Here is a web app that demonstrates and lets you play with tilings constructed from parallel grids.

In the app, click on one of the lines in the pentagrid on the left. You'll see a single "ribbon" of tiles highlighted in the Penrose tiling on the right. Suppose that this ribbon is periodic. That would mean that after some arbitrary number of tiles, the same sequence of tiles in that same sequence of orientations would repeat. Furthermore, this sequence must be finite, and because it is only composed of two tiles, we can determine the ratio of those two tiles in that finite sequence.[br][br]Tile Ratio = # of tile A / # of tile B[br][br]This ratio must be a rational number, because our finite sequence must have a finite integer number for each # of tiles. Otherwise, the sequence cannot be finite, and the pattern cannot be periodic.[br][br]We can directly calculate the number of tiles in our Penrose ribbon, because the tiles correspond to the intersections of lines within our pentagrid.[br][br]Lets say tile A corresponds to the lines that intersect at 36 degrees, and tile B corresponds to the ones that intersect at 72 degrees. The spacing between our parallel lines for each type of intersection is defined by:[br][br][math]\frac{1}{sin\left(\alpha^{\circ}\right)}[/math][br][br]Where alpha is the angle of intersection.

So the ratio of tile A to tile B in the sequence is the same as the ratio of these distances along a given line.[br][br]Hence,[br][br][math]T_r=\frac{\frac{1}{sin\left(36^{\circ}\right)}}{\frac{1}{sin\left(72^{\circ}\right)}}=\frac{sin\left(72^{\circ}\right)}{sin\left(36^{\circ}\right)}=1.618...=\varphi\notin\mathbb{Q}[/math][br][br]Because this ratio is irrational, we know that there cannot be a periodic sequence of tiles along this parallel line, and more generally, along any line within our pentagrid. Hence the pattern formed by the pentagrid must be aperiodic.