Der Zylinder
Im Folgenden wirst du den Zylinder erkunden.[br]Halte alle deine Ergebnisse schriftlich fest.
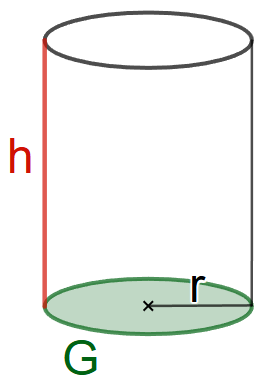
[i]Definition[br][/i][b][br]Aufgabe 1: Übertrage[/b] den folgenden Merktext und die Zeichnung in deine Unterlagen.[br][br]"Ein Zylinder ist ein Körper mit der Höhe [i]h[/i], dessen Grundflächen [i]G[/i] zwei kongruente Kreise mit dem Radius [i]r [/i]sind."[br]

[i]Grundfläche[/i][br][br][b]Aufgabe 2:[/b] Die Grundfläche des Zylinders ist ein Kreis.[br] [b]Berechne [/b]jeweils den Flächeninhalt und den Umfang der Grundflächen mit folgenden Radien:
i) [math]r=5cm[/math]
ii) [math]r=12cm[/math]
iii) [math]r=xcm[/math], [math]x\in[/math][img]https://wikimedia.org/api/rest_v1/media/math/render/svg/786849c765da7a84dbc3cce43e96aad58a5868dc[/img]
[i]Oberflächeninhalt[/i][br][br]Aufgabe 3: Betrachte die folgenden Zylinder mit Radius [i]r[/i] und Höhe [i]h[/i].[br] a) [b]Gib [/b]eine Formel für die Länge der Kreislinie (hellblau) in Abhängigkeit des Radius [i]r[/i] [b]an[/b].[br] b) Ziehe den roten Punkt, um das Netz des Zylinders zu entwickeln.[br] [b]Stelle [/b]eine Formel für die Mantelfläche (rosa) [b]auf[/b].[br] c) [b]Stelle [/b]nun eine Formel für den kompletten Oberflächeninhalt des Zylinders [b]auf[/b].
Kontrolliere dein Ergebnis aus c):
d) Berechne den Oberflächeninhalt eines Zylinders mit [math]r=5cm[/math] und [math]h=12cm[/math]
[i]Volumen[/i][b][br][br]Aufgabe 4: [/b]Betrachte das Prisma, welches sich im Zylinder befindet.[br] Verändere die Anzahl der Ecken.[br] a) [b]Beschreibe [/b]wie sich das Prisma verändert. Wie verhält sich dies zum Zylinder? [br] b) [b]Vergleiche [/b]das Volumen des Prismas mit dem Produkt der Grundfläche und Höhe des Zylinders. [br] Welche Formel für das Volumen lässt sich so aufstellen?[br] c) Verändere den Radius und die Höhe. Bleibt deine Beobachtung gleich?[br]
Kontrolliere dein Ergebnis aus b):
d) Berechne das Volumen eines Zylinders mit [math]r=5cm[/math] und [math]h=12cm[/math]