Las Cónicas con geogebra
Table of Contents
- INTRODUCCIÓN
- Introducción
- Geogebra: controladores y applets
- Definiciones
- Tipos de cónicas y su definición
- Parábola
- Parábola: Definición, gráfica y ecuaciones
- Antena parabólica
- Circunferencia
- Circunferencia: Definición, gráfica y ecuaciones
- Elipse
- Elipse: Definición, gráfica y ecuaciones
- Hipérbola
- Hipérbola: Definición, gráfica y ecuaciones
- Síntesis de ecuaciones de cónicas cuando B = 0
- Síntesis de ecuaciones de cónicas cuando B = 0
- Ecuación general de segundo grado
- Ecuación general de segundo grado
- Libros geogebra
- Libros geogebra profedomingohely
Introducción
El objetivo del libro geogebra es analizar el desarrollo de los cuerpos geométricos de los poliedros y los cuerpos redondos.[br][br]De los poliedros se analizan prismas y pirámides rectos con base polígono regular y rect [br][br]
Tipos de cónicas y su definición
[b]CÓNICAS[/b][br][br]Las curvas llamadas cónicas son lugares geométricos de puntos que cumplen ciertas propiedades en términos de la distancia. También son las curvas que se obtienen por la intersección de un cono circular recto y un plano, dependiendo del ángulo de inclinación del plano.[br][br]Las cónicas se clasifican en 4 tipos: parábola, circunferencia, elipse e hipérbola. [br][br][b]Parábola[/b]: [br][br]- Es el lugar geométrico de los puntos del plano tales que su distancia a un punto fijo llamado foco es igual a su distancia a una recta fija llamada directriz.[br][br]- Es la curva formada cuando el plano que interseca al cono es paralelo a su generatriz.[br][br][b]Circunferencia: [br][/b][br]- Es el lugar geométrico de los puntos del plano tales que su distancia a un punto fijo llamado centro es constante.[br][br]- Es la curva formada cuando el plano que interseca al cono es perpendicular a su eje.[br][br][b]Elipse[/b]: [br][br]- Es el lugar geométrico de los puntos del plano tales que la suma de las distancias a dos puntos fijos llamados focos es una constante.[br][br]- Es la curva formada cuando el plano que interseca al cono no es paralelo a su generatriz.[br][br][b]Hipérbola[/b]: [br][br]-Es el lugar geométrico de los puntos del plano tales que la diferencia de las distancias a dos puntos fijos llamados focos es una constante. [br][br]- Es la curva formada cuando el plano que interseca al cono es paralelo a su eje. [br][br]A continuación se presenta un applet que permite mostrar cada una de las cónicas a medida que se modifica la posición del plano intersectante.[br][br]Con fines didácticos se utiliza un plano para cada cónica:[br][br]- El plano que muestra la [b]parábola[/b] se mueve transladando el punto [b]P[/b].[br][br]- El plano que muestra la [b]circunferencia[/b] se mueve transladando el punto [b]C[/b]. [br][br]- El plano que muestra la [b]elipse[/b] se mueve transladando los puntos [b]E[sub]1[/sub][/b] y [b]E[/b][sub][b]2[/b].[br][br][/sub]- El plano que muestra la [b]hipérbola[/b] se mueve transladando el punto [b]H[/b].[br][br]Por otra parte se tiene que:[br][br]- La altura del cono se modifica al trasladar el punto [b]B[/b].[br][br]- El radio de la base del cono se modifica al trasladar el punto [b]A[sub]R[/sub][/b].[br][br]- El cono se puede rotar libremente arrastrando el puntero del mouse en cualquier sitio de la pantalla activa.
Cada una de las cónicas se expresa mediante su [b]ecuación canónica[/b] pero todas son casos particulares de la [b]ecuación general de segundo grado, Ax[sup]2[/sup] + Bxy + Cy[sup]2[/sup] + Dx + Ey + F = 0[/b].[br][br]En las secciones siguientes se abordará cada cónica por separado y al final se estudiará la ecuación general, haciendo énfasis en la parte gráfica.
Parábola: Definición, gráfica y ecuaciones
[b]Contenido[br][br][/b]- Conceptos[br][br]- Parábolas con eje focal vertical[br][br]- Parábolas con eje focal horizontal
[b]Parábola[/b] es el lugar geométrico de los puntos del plano tales que su distancia a un punto fijo llamado foco es igual a su distancia a una recta fija llamada directriz: [b]distancia FP = distancia PA[/b].[br][br]En la figura se muestra una parábola con eje de simetría o eje focal vertical, es decir, paralelo al eje Y y sus ramas abren hacia arriba. También se dice que es convexa o que es cóncava hacia arriba.[br][br]Cualquiera que sea la orientación de la parábola, se tienen los siguientes elementos:[br][br][br][b]Vértice, V = (h, k)[/b]: Es el puto de intersección de la parábola y el eje focal o de simetría. También es el punto extremo de la gráfica: [br][br]- Si es cóncava hacia arriba, el vértice es el punto mínimo (más bajo)[br][br]- Si es cóncava hacia abajo, el vértice es el punto máximo (más alto)[br][br]- Si es cóncava hacia la derecha, el vértice es el punto de menor abcisa (más a la izquierda)[br][br]- Si es cóncava hacia la izquierda, el vértice es el punto de mayor abcisa (más a la derecha)[br][br]Las coordenadas del vértice se designan por [b](h, k)[/b].[br][br]En la figura, el vértice es el punto (2, -2). Es decir, h = 2, k = -2.
[b]Eje focal o eje de simetría[/b]: Es la recta que divide a la parábola en dos mitades congruentes. Pasa por el vértice y por el foco. En la figura corresponde a la recta x = 2.[br][br][b]Parámetro, p[/b]: Es la distancia entre el foco y el vértice o entre el vértice y la directriz. Siempre es positivo porque es una distancia. En la figura p = 1.[br][br][b]Foco, F[/b]: Es el punto fijo de la parábola. Está ubicado sobre el eje focal a una distancia igual al parámetro [b]p[/b] En la figura, las coordenadas del foco son (2, -1).[br][br][b]Directriz[/b]: Es una recta perpendicular al eje focal a una distancia igual al parámetro [b]p[/b]. En la figura corresponde a la recta y = -3 (pasa por [b]A[/b])[br][br][b]Radio vector, PF[/b]: Es cada uno de los segmentos que unen el foco con un punto cualquiera de la parábola.[br][br][b]Lado recto, MN[/b]: Es el segmento paralelo a la directriz, pasa por el foco y los extremos [b]M[/b] y [b]N[/b] son puntos opuestos de la parábola. Su longitud es [b]4p[/b]. En el ejemplo, el lado recto mide [b]4[/b].[br][br] El lado recto se puede utilizar para dibujar de manera aproximada una parábola cuando se conoce la concavidad, el valor del parámetro y las coordenadas del vértice o del foco o ecuación de la directriz, dado que se obtienen tres puntos de la parábola: Vértice [b]V[/b] y los dos extremos del lado recto, [b]M[/b] y [b]N.[/b]
A continuación se presentan dos applets:[br][br]- Parábola con eje de simetría vertical[br][br]- Parábola con eje de simetría horizontal[br][br][b]Parábola con eje de simetría vertical[/b][br][br]Se consideran dos casos: cóncava hacia arriba (las ramas abren hacia arriba) y cóncava hacia abajo (las ramas abren hacia abajo).[br][br]Puede seguir los siguientes pasos:[br][br]1. Seleccione la concavidad.[br][br]2. Determine los valores [b]h[/b], [b]k[/b], [b]p[/b]. Se puede hacer utilizando los deslizadores o ingresando el valor en las casillas de entrada. Si [b]h = 0[/b] y [b]k = 0[/b] se tiene que el vértice está en el origen del plano cartesiano.[br][br]3. Active/desactive las casillas de verificación Vértice, Eje de simetría, Foco, Directriz y Radios vectores AP y PF.
4. Desplace el punto [b]A[/b] de la directriz y observe la posición de [b]P[/b]. Se puede comprobar que [b]PF = PA[/b] dado que son radios de la circunferencia con centro en [b]P[/b].[br][br]Si se activa el botón [b]Activa Rastro[/b], el punto [b]P[/b] va dejando su huella o rastro. El rastro se puede desactivar o borrar. Se puede verificar que la gráfica corresponde a la huella que deja el punto [b]P[/b].[br][br]5. Active el proceso de construcción. [br][br]6. Active la ecuación canónica de la parábola:[br][br] - Si la concavidad es hacia arriba, la ecuación es de la forma [math]\left(x-h\right)^2=4p\left(y-k\right)[/math].[br][br] - Si la concavidad es hacia abajo, la ecuación es de la forma [math]\left(x-h\right)^2=-4p\left(y-k\right)[/math].[br][br]Así por ejemplo,[br][br]a) Ecuación canónica: [math]\left(x-2\right)^2=4\left(y+1\right)[/math], [b]h = 2[/b], [b]k = -1[/b], [b]4p = 4[/b]. Por lo tanto,[br][br] V = (2, -1), p = 1 y la concavidad de la parábola es hacia arriba porque 4p es [b]positivo[/b].[br][br] Eje focal: x = 2 F = (2, 0) Directriz: y = -2 Lado recto = 4: M = (0, 0) N = (4, 0)[br][br]b) Ecuación canónica: [math]\left(x-1\right)^2=-8\left(y-2\right)[/math], [b]h = 1[/b], [b]k = 2[/b], [b]-4p = - 8[/b]. Por lo tanto,[br][br] V = (1, 2), p = 2 y la concavidad de la parábola es hacia abajo porque 4p es [b]negativo[/b].[br][br] Eje focal: x = 1 F = (1, 0) Directriz: y = 4 Lado recto = 8: M = (-3, 0) N = (5, 0)[br][br] 7. Active la ecuación general. En los dos casos de concavidad de la parábola con eje focal vertical es de la forma [math]Ax^2+Dx+Ey-F=0[/math] donde A, D, E y F son los coeficientes que resultan al desarrollar los productos indicados de la ecuación canónica. [br][br]Para el ejemplo a) la ecuación general es [math]x^2-2x+8y-15=0[/math][br][br]Para el ejemplo b) la ecuación general es [math]x^2-4x-4y=0[/math][br][br]La ecuación general de la parábola se obtiene al desarrollar los productos indicados de la ecuación canónica.[br][br]Le ecuación canónica se obtiene factorizando la ecuación general. Normalmente se hace por el método de completar cuadrados.[br][br]La ecuación general de la parábola es un caso particular de la ecuación general de segundo grado [br] [math]Ax^2+Bxy+Cy^2+Dx+Ey+F=0[/math]. Cuando el eje focal es vertical se tiene la [b]función cuadrática[/b] [math]f\left(x\right)=ax^2+bx+c[/math]. [i] Ver Función cuadrática en el libro Funciones: https://www.geogebra.org/m/ybhvuukp#material/cjzfnycw[/i][br]
[b]Parábola con eje de simetría horizontal[/b][br][br]También se consideran dos casos: cóncava hacia la derecha (las ramas abren hacia la derecha) y cóncava hacia la izquierda (las ramas abren hacia la izquierda).[br][br]En este applet se aplica la misma metodología del applet anterior.[br][br]La ecuación canónica es de la forma [math]\left(y-k\right)^2=\pm4p\left(x-h\right)[/math]. Si la parábola abre a la derecha el segundo miembro de la ecuación es positivo. Si abre hacia la izquierda, es negativo.[br][br]Ejemplo:[br][br]De la parábola cuya ecuación es [math]\left(y-1\right)^2=-8\left(x+2\right)[/math] se puede concluir que:[br][br] h = -2 k = 1 V = (-2, 3) p = 2 F = (-4, 1) Directriz: x = 0 Eje focal: y = 1[br] [br] Longitud lado recto = 8: M = (-4, -3) N = (-4, 5) [br][br] La parábola es cóncava hacia la izquierda.[br][br]La ecuación general de una parábola con eje focal horizontal está dada por [math]Cy^2+Dx+Ey+F=0[/math]. Los coeficientes [b]A[/b] y [b]B[/b] de la ecuación general son iguales a cero.[br][br]La ecuación general de la parábola de este ejemplo es [math]y^2+8x-2y+17=0[/math].
Circunferencia: Definición, gráfica y ecuaciones
[b]Contenido[br][br][/b]- Conceptos[br][br]- Gráfica y ecuaciones
[b]Circunferencia[/b]:[br][br]Es el lugar geométrico de los puntos del plano tales que su distancia a un punto fijo llamado [b]centro[/b] es constante. Las coordenada del centro de la circunferencia son [b]C = (h, k)[/b].[br][br][b]Radio, R[/b]: Es la distancia entre un punto de la circunferencia y el centro. [b]R = d(PC)[/b].[br][br]A continuación se presenta un applet que permite mostrar la circunferencia y sus ecuaciones de acuerdo con la ubicación del centro y la medida del radio.[br][br]Si se muestra el radio, se activa un deslizador. Su función es desplazar el punto [b]P[/b] al rededor de [b]C[/b]. Active el rastro para observar su huella. Recuerde que el rastro se puede desactivar y/o borrar.[br][br][b]Ecuaciones de la circunferencia[br][br][/b]- [b]Ecuación canónica o estándar[/b]. Es de la forma [math]\left(x-h\right)^2+\left(y-k\right)^2=R^2[/math][br][br] Si [b]C = (-1, 3)[/b] y [b]R = 4[/b], la ecuación canónica es [math]\left(x+1\right)^2+\left(y-3\right)^2=16[/math][br][br] Si el centro es el origen del sistema de coordenadas, [b]h = 0[/b], [b]k = 0[/b], la ecuación canónica es de la forma [math]x^2+y^2=R^2[/math][br][br]- [b]Ecuación general[/b]. Es de la forma [math]Ax^2+Cy^2+Dx+Ey+F=0[/math] siendo [b]A = C[/b]. Al igual que sucede con las otras cónicas, la ecuación general de la circunferencia es un caso particular de la ecuación de segundo grado [math]Ax^2+Bxy+Cy^2+Dx+Ey+F=0[/math].[br][br]La ecuación general de la circunferencia del ejemplo anterior es [math]x^2+y^2+2x-6y-6=0[/math]. Se obtiene al desarrollar los productos indicados de la ecuación canónica.[br][br]Le ecuación canónica se obtiene factorizando la ecuación general. Normalmente se hace por el método de completar cuadrados.[br]
Elipse: Definición, gráfica y ecuaciones
[b]Contenido[/b][br][br]- Conceptos[br][br]- Elipse con eje focal horizontal[br][br]- Elipse con eje focal vertical[br][br]- Otro procedimiento de construcción de la elipse[br][br][br][b]Elipse[br][/b][br]Es el lugar geométrico de los puntos del plano tales que la suma de las distancias a dos puntos fijos llamados focos es una constante: [math]distancia\left(F_1P\right)+distancia\left(PF_2\right)=2a[/math]. La constante es [b]2a[/b] y equivale a la [b]medida del eje mayor[/b] de la elipse.
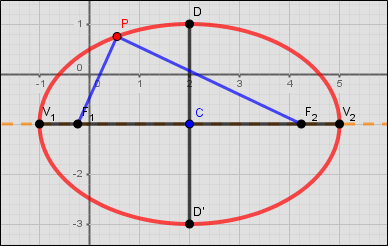
Cualquiera que sea la orientación de la elipse, se tienen los siguientes elementos:[br][br][b]Centro, C = (h, k)[/b]: Es el puto de intersección entre el eje mayor y el eje menor. Es el punto medio de cada uno de los dos ejes de la elipse. También es el punto de simetría de la elipse.[br][br][b]Eje mayor, [math]V_1V_2[/math][/b]: Es el segmento de mayor distancia entre dos puntos opuestos de la elipse. Contiene los dos vértices y los dos focos de le elipse. [br][br]La longitud del [b]eje mayor[/b] es [b]2a[/b]. Por lo tanto [b]a[/b] es la longitud del [b]semieje mayor[/b]. Equivale a la distancia [math]CV_1[/math] o [math]CV_2[/math]. [br][br][b]Eje menor, [math]DD'[/math][/b]: Es el segmento mediatriz del eje mayor. Sus extremos son puntos opuestos de la elipse.[br][br]La longitud del [b]eje menor[/b] es [b]2b[/b]. Por lo tanto [b]b[/b] es la longitud del [b]semieje menor[/b].[br][br][b]Focos, [math]F_1[/math][/b] y [math]F_2[/math]: Son dos puntos fijos de la elipse que hacen que la suma de las distancias de ellos a un punto de la elipse sea una constante. Son simétricos al centro de la elipse y se ubican en el eje mayor.[br][br][b]Eje focal[/b]: Es la recta que pasa por el centro y contiene los focos y los vértices de la elipse.[br][br][b]Semidistancia focal, c[/b]: Es la distancia entre el centro y uno cualquiera de los focos, es decir, la distancia [math]CF_1[/math] o [math]CF_2[/math]. [br][br][b]Relación entre semieje mayor, semieje menor y semidistancia focal[/b]:[br][br]La relación es pitagórica: [math]\left(semiejemayor\right)^2=\left(semiejemenor\right)^2+\left(semidistanciafocal\right)^2[/math][br][br] [math]a^2=b^2+c^2[/math] [math]\Longrightarrow[/math] [math]c=\sqrt{\left(a^2-b^2\right)}[/math][br] [br][b]Excentricidad, [math]\epsilon[/math][/b]: Es la razón entre la semidistancia focal y el semieje mayor. [math]\epsilon=\frac{c}{a}[/math] Su valor se encuentre entre cero y uno. [br][br]A continuación se presentar tres applets con una metodología similar a los applets de la parábola.[br][br]- Elipse con eje focal horizontal[br][br]- Elipse con eje focal vertical[br][br]- Otro procedimiento de construcción de la elipse[br][br][br][b]Applet 1. Elipse con eje focal horizontal[br][br][/b]- Dar los valores [b]h, k, a, b[/b]. Tenga en cuenta que [b]a > b[/b]. Se puede hacer en las casillas de entrada o con los deslizadores.[br][br]- Activar [b]Centro, eje mayor, vértices, eje menor [/b]y [b]focos[/b]. La aplicación calcula automáticamente el valor de [b]c[/b].
- Activar [b]proceso de construcción[/b]. Se visualiza el proceso de construcción: El punto [b]P[/b] es un punto de la elipse. Activando el rastro y desplazando el punto [b]A[/b] sobre la circunferencia generatriz, [b]P[/b] deja la huella que es la elipse que cumple las condiciones definidas al comienzo del applet. Se puede comprobar si se activa [b]gráfica[/b].[br][br]- Activar [b]radios vectores[/b], segmentos [math]F_1P[/math] y [math]PF_2[/math][br][br]- Activar [b]Comprobar definición[/b]. Se muestra una demostración geométrica y la comprobación mediante una tabla de valores: las medida de cada radio vector varía pero su suma siempre es [b]2a[/b].[br][br]Otra comprobación se obtiene cuando [b]P[/b] coincide con [math]V_1[/math]. En este caso [math]PF_1=V_1F_1=F_2V_2[/math] y por lo tanto la suma de los dos radio vectores equivale a la distancia entre vértices, la cual es [b]2a[/b].[br][br]- Activar [b]excentricidad[/b]. Se observa que siempre está entre cero y uno. A medida que [b]b[/b] se acerca a [b]a[/b], [b]c[/b] se acerca a cero. Cuando esto sucede, los dos focos coinciden con el centro y la elipse se convierte en una circunferencia. Por eso se puede afirmar que la circunferencia es un caso particular de la elipse.[br][br]- Activar [b]ecuación canónica[/b]. Cuando el eje focal es horizontal la ecuación es de la forma [math]\frac{\left(x-h\right)^2}{a^2}+\frac{\left(y-k\right)^2}{b^2}=1[/math][br][br]Un ejemplo: Si una elipse tiene su eje focal horizontal y [b]C = (2,-1)[/b], [b]a = 3[/b], [b]b = 2[/b], la ecuación canónica es [math]\frac{\left(x-2\right)^2}{9}+\frac{\left(y+1\right)^2}{4}=1[/math] .[br][br]Otros datos que se pueden obtener son:[br][br]- semidistancia focal, [math]c=2.24[/math][br][br]- Excentricidad, [math]\epsilon=0.75[/math] [br][br][i]Observación: Si [b]h = 0[/b] y [b]k = 0[/b] se tiene que el centro de la elipse es el origen del sistema de coordenadas y la ecuación canónica es [math]\frac{x^2}{a^2}+\frac{y^2}{b^2}=1[/math][/i][br][br]- Activar [b]ecuación general[/b]. Para la elipse del ejemplo anterior, la ecuación es [math]4x^2+9y^2-16x+18y-11=0[/math]. Se observa que [b]A[/b] de [math]x^2[/math] y [b]B[/b] de [math]y^2[/math] son positivos.
[b]Applet 2. Elipse con eje focal vertical[br][br][/b]Es un applet con las mismas características del anterior.[br][br]En este caso, el eje mayor es vertical y el eje menor es horizontal.
Vale la pena destacar que la ecuación canónica de una elipse determina el sentido del eje mayor dado que los denominadores son [b]a[/b] y [b]b[/b]. Además, siempre se cumple que [b]a > b[/b]:[br][br]- Si el denominador mayor es el denominador de [b]x[/b], el eje focal es horizontal.[br][br]- Si el denominador mayor es el denominador de [b]y[/b], el eje focal es vertical.[br][br][i]Si [b]a = b[/b], la elipse se convierte en circunferencia porque los dos focos coinciden con el centro.[/i]
[b]Applet 3. Otro procedimiento de construcción de la elipse[br][/b][br]En el applet se muestra un procedimiento geométrico para dibujar una elipse con el eje focal horizontal.[br][br]Active el proceso de construcción. Active el rastro y desplace el dial del deslizador. El punto [b]P[/b] deja su huella . La huella es una elipse con eje horizontal y se puede confrontar cuando se activa Gráfica.
Hipérbola: Definición, gráfica y ecuaciones
[b]Contenido[/b][br][br]- Conceptos[br][br]- Hipérbola con eje focal horizontal[br][br]- Hipérbola con eje focal vertical[br][br][br][b]Hipérbola[/b][br][br]Es el lugar geométrico de los puntos del plano tales que la diferencia de las distancias a dos puntos fijos llamados focos es una constante: [math]distancia\left(F_1P\right)-distancia\left(PF_2\right)=2a[/math]. La constante es [b]2a[/b] y equivale a la [b]medida del eje transverso[/b] de la hipérbola.
En la figura se muestra una hipérbola con eje focal horizontal. En ella se detallan los diferentes elementos:[br][br][b]Centro, C = (h, k)[/b]. Es el puto de intersección entre el eje transverso y el eje conjugado. Es el punto medio de cada uno de los dos ejes de la hipérbola.[br][br][b]Eje transverso, [math]V_1V_2[/math][/b]: Es el segmento entre los dos vértices.[br][br]La longitud del eje transverso es [b]2a[/b]. Por lo tanto [b]a[/b] es la longitud del semieje transverso. Equivale a la distancia [math]CV_1[/math] o [math]CV_2[/math]. [br][br][b]Eje conjugado, [math]DD'[/math][/b]: Es el segmento mediatriz del eje transverso. Su longitud es [b]2b[/b], por lo tanto, [b]b[/b] es la longitud del [b]semieje conjugado[/b].[br][br]Cuando el eje conjugado tiene igual longitud que el eje transverso, [b]a = b[/b], se tiene una [b]hipérbola equilátera[/b].[br][br][b]Focos[/b], [math]F_1[/math] y [math]F_2[/math]: Son dos puntos fijos de la hipérbola que hacen que la diferencia de las distancias de ellos a un punto de la hipérbola sea una constante. Son simétricos al centro de la hipérbola y se ubican en la prolongación del eje transverso.[br][br][b]Eje focal[/b]: Es la recta que pasa por el centro y contiene los focos y los vértices de la hipérbola.[br][br][b]Semidistancia focal, c[/b]: Es la distancia entre el centro y uno cualquiera de los focos, es decir, la distancia [math]CF_1[/math] o [math]CF_2[/math]. [br][br][b]Relación entre semieje transverso, semieje conjugado y semidistancia focal[/b]:[br][br]La relación es pitagórica pero a diferencia de la elipse, [b]c[/b] es mayor que [b]a[/b] y mayor que [b]b[/b]. Así, [br][math]\left(semidistanciafocal\right)^2=\left(semiejetransverso\right)^2+\left(semiejeconjugado\right)^2[/math] [math]\Longrightarrow[/math] [math]c^2=a^2+b^2[/math][br][br][b]Excentricidad[/b], [math]\epsilon[/math]: Es la razón entre la semidistancia focal y el semieje transverso, [math]\epsilon=\frac{c}{a}[/math]. Dado que [b]c > a[/b], la excentricidad de la hipérbola siempre es mayor que la unidad, [math]\epsilon[/math] > 1.[br][br][b]Asíntotas[/b]: Son dos rectas que pasan por el centro de la hipérbola a las cuales sus ramas se va acercando indefinidamente. [br][br]Para graficar las asíntotas de la hipérbola basta con trazar las diagonales del rectángulo con centro en [b]C[/b] y sus lados son eje transverso y eje conjugado.[br][br]Las asíntotas permiten hacer una gráfica aproximada de la hipérbola: se ubican los vértices y se trazan las asíntotas.[br][br]Se presentan dos applets de la hipérbola. El primero con eje focal horizontal y el segundo con eje focal vertical.
[b]Ecuación canónica y ecuación general de la hipérbola[br][br]Ecuación canónica[/b]: [br][br]- Si el eje focal es horizontal, la ecuación canónica es de la forma [math]\frac{\left(x-h\right)^2}{a^2}-\frac{\left(y-k\right)^2}{b^2}=1[/math].[br][br]- Si el eje focal es vertical, la ecuación canónica es de la forma [math]\frac{\left(y-k\right)^2}{a^2}-\frac{\left(x-h\right)^2}{b^2}=1[/math].[br][br]Dos observaciones importantes:[br][br]1. La ecuación canónica es la diferencia entre dos términos racionales. El primer término (minuendo) siempre es positivo y determina la dirección del eje focal. Si el término de [b]x[/b] es positivo, la hipérbola tiene su eje focal horizontal. Si el término de [b]y[/b] es positivo, la hipérbola tiene su eje focal vertical. [br][br]2. La longitud del semieje transverso es el denominador del término positivo independientemente si es mayor, menor o igual que la longitud del eje conjugado.[br][br]Ejemplo:[br][br]Sean dos hipérbolas definidas por su ecuación canónica:[br][br]a) [math]\frac{\left(x-2\right)^2}{9}-\frac{\left(y+1\right)^2}{4}=1[/math] b) [math]\frac{\left(y-2\right)^2}{4}-\frac{\left(x+1\right)^2}{9}=1[/math][br][br]- Eje focal de la primera es horizontal y el eje focal de la segunda es vertical.[br][br]- Eje transverso y eje conjugado: En la primera, [math]a=\sqrt{9}=3[/math] y [math]b=\sqrt{4}=2[/math], a > b. En la segunda, [math]a=\sqrt{4}=2[/math] [math]b=\sqrt{9}=3[/math], a < b.[br][br]- Centro: En la primera, C = (2, -1). En la segunda, C = (-1, 2).[br][br][b]Ecuación general de la hipérbola[/b]:[br][br]Sea que el eje focal es horizontal o vertical, la ecuación general es de la forma [math]Ax^2+Cy^2+Dx+Ey+F=0[/math][br]. Se puede observar en los dos applets que los coeficientes [b]A[/b] y [b]C[/b] tienen signos distintos.[br][br]La ecuación general de la hipérbola, al igual que en las otras cónicas, es un caso particular de la ecuación general de segundo grado [math]Ax^2+Bxy+Cy^2+Dx+Ey+F=0[/math]. Esta ecuación se analiza en el siguiente capítulo.
Síntesis de ecuaciones de cónicas cuando B = 0
Se presenta un resumen de las ecuaciones de las cónicas cuando el eje focal es paralelo a uno de los ejes del plano cartesiano. Esto se presenta cuando el término rectangular [b]Bxy[/b] de la ecuación general de segundo grado es nulo.[br][br]La ecuación general con [b]Bxy[/b] nulo es de la forma [math]Ax^2+Cy^2+Dx+Ey+F=0[/math] porque [b]B = 0[/b].[br][br]Con excepción de la circunferencia, la ecuación canónica de las cónicas depende de la orientación del eje focal.
La ecuación general de segundo grado se analiza en el siguiente capítulo. Son dos casos que se tienen: Cuando [math]B=0[/math] y cuando [math]B\ne0[/math].[br][br]En el primer caso, el eje focal es paralelo a uno de los ejes de coordenadas.[br][br]En el segundo caso, el eje focal sufre una rotación.
Ecuación general de segundo grado
[b]Contenido[br][br][/b]- Ecuación general cuando [math]B=0[/math][br][br]- Ecuación general cuando [math]B\ne0[/math][br][br]- Discriminante de las cónicas[br][br][br]La ecuación general de segundo grado, también llamada ecuación de las cónicas, es de la forma [math]Ax^2+Bxy+Cy^2+Dx+Ey+F=0[/math]. El término [math]Bxy[/math] es llamado [b]término rectangular[/b].[br][br]Cuando el término rectangular es nulo ([b]B = 0[/b]), el eje focal de la cónica es paralelo a uno de los ejes coordenados.[br][br]Cuando el término rectangular no es nulo ([math]B\ne0[/math]), el eje focal de la cónica no es paralelo a uno de los ejes coordenados sino que sufre una rotación con relación a ellos.[br][br][b]Discriminante de las cónicas[br][br][/b]Discriminante es la expresión [math]B^2-4AC[/math]. Su resultado indica el tipo de cónica como se detalla en la siguiente tabla. [br][br]No siempre la ecuación general de segundo grado define una parábola, una elipse, una circunferencia o una hipérbola. Se presentan casos especiales dependiendo de los valores de los coeficientes de la ecuación:[br][br]- Cuando el [b]discriminante es cero[/b] se puede tener parábola, dos rectas paralelas, una recta o conjunto vacío. [br][br]- Cuando el [b]discriminante es menor que cero[/b] se puede tener elipse, circunferencia, un punto o conjunto vacío.[br][br]- Cuando el [b]discriminante es mayor que cero[/b] se puede tener hipérbola o dos rectas secantes.
[b]Ecuación general de segundo grado cuando B = 0[br][br][/b]Cuando [b]B = 0[/b], el discriminante quede reducido a la expresión [b]- 4AC[/b]. Se presentan tres casos:[br][br]1. [math]-4AC=0[/math]. La ecuación es de [b]tipo parabólico[/b] cuando [b]A[/b] o [b]C[/b] o [b]las dos[/b] sean iguales a cero. [br][br]2. [math]-4AC<0[/math]. La ecuación es de [b]tipo elíptico[/b] cuando [b]A[/b] y [b]C[/b] son de igual signo (los dos coeficientes negativos o los dos positivos).[br][br]3. [math]-4AC>0[/math]. La ecuación es de [b]tipo hiperbólico[/b] cuando [b]A[/b] y [b]C[/b] son de signos contrarios.[br][br]El applet que se presenta permite mostrar los diferentes casos cuando en la ecuación general [b]B = 0[/b].[br][br]- Se puede modificar la escala: Botón Alejar, Botón Aproximar.[br][br]- Se puede mostrar información adicional a cada ecuación definida: Botón Sí, Botón No.
Explore ejemplos que cumplan cada una de las siguientes condiciones. Analice el valor del discriminante y la información que se presenta:[br][br]a) [math]A=0,C\ne0[/math][br][br]b) [math]A\ne0,C=0[/math][br][br]c) [math]A=0,C=0[/math][br][br]d) [math]A=0,C\ne0,D=0[/math][br][br]e) [math]A\ne0,C=0,E=0[/math][br][br]f) [math]A=0,C=0,D=0,E\ne0[/math][br][br]g) [math]A=0,C=0,E=0,D\ne0[/math][br][br]h) [math]A=3,C=0,D=0,E=0,F=8[/math][br][br]i) [math]A>0,C>0[/math][br][br]j) [math]A<0,C<0[/math][br][br]k) [math]A=C[/math][br][br]l) [math]A\cdot C>0,D=0,E=0,F=0[/math] [br][br]m) [math]A=1,C=2,D=3,E=6,F=10[/math][br][br]n) [math]A>0,C<0[/math][br][br]o) [math]A<0,C>0[/math][br][br]p) [math]A\cdot C<0,D=0,E=0,F=0[/math]
[b]Ecuación general de segundo grado[/b][br][br]Como ya se indicó, cuando el término rectangular es nulo ([b]B = 0[/b]), el eje focal de la cónica es paralelo a uno de los dos ejes coordenados, mientras que si [math]B\ne0[/math], el eje focal queda rotado. Esto se puede visualizar en el segundo applet.
Para obtener un ejemplo de ecuación de tipo parabólico, buscar valores de B, A, C que cumplan que [math]B^2=4AC[/math]. Por ejemplo, B = 4, A = 2, C = 2 o B = 4, A = 1, C = 4.
Libros geogebra profedomingohely
Abrir, https://www.geogebra.org/m/pckktn56