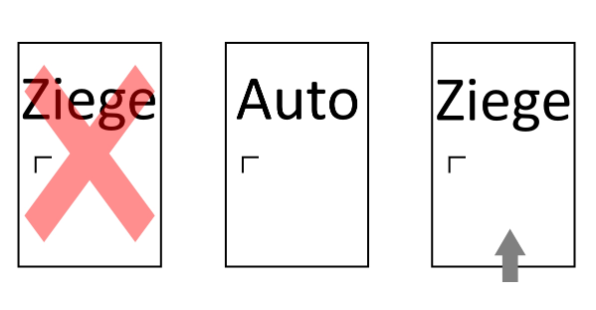
Ausgangslage: [br][list][*]Hinter 3 verschlossenen Türen stehen 2 Ziegen und ein Auto.[/*][*]Wählt der Kandidat die richtige Tür, gewinnt er das Auto.[/*][/list][br][br]Die Show beginnt:[br][list=1][*]Der Kandidat überlegt und wählt eine Tür.[/*][*]Der Moderator öffnet eine der anderen Türen mit Ziege.[/*][*]Der Kandidat darf nun wechseln oder bei seiner ersten Wahl bleiben.[/*][/list][br][br]Unterscheide im Folgenden die beiden Fälle: [b][u]nicht wechseln[/u][/b] und [u][b]wechseln[/b][/u][br][br][list][*]Zeichne für beide Fälle ein Baumdiagramm, in dem die Wahrscheinlichkeiten ersichtlich sind. [/*][*]Bestimme für beide Fälle die Wahrscheinlichkeiten, dass der Kandidat das Auto gewinnt.[/*][/list][br][br][br]

[i][size=85]Bemerkung:[br]Bis zu dem Moment, wo der Kandidat das erste Mal wählt, ist es ein Laplace-Experiment.[br]Ab dem Moment, wo der Moderator eine Tür öffnet, ist das gesamte Experiment kein Laplace-Experiment mehr.[/size][/i][size=85][i][br][br][br][/i][/size]