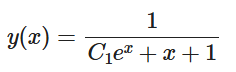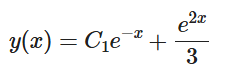
1階線形は積微分と部分積分で
[b]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[br][/b][br]今回も、方程式のタイプに応じた解法となる、基本的な視点をふやそう。[br][br]微分方程式で式が単純なのは、もちろん微分が1階(1回)だけで、式も線形のものだ。[br]だから、1階線形のタイプについて、さらに視点をふやしてみよう。[br][br][color=#0000ff][b]yのn階微分をy(n)と書き、Akがxの関数、ΣAk*y(k)=0のとき、線形同次[/b]。[br][/color]Akが定数なら、特に、定数線形同次というね。[br]線形だとしても、さらに、=0ではなく、[b]=B(x)[/b]のとき、それぞれ[color=#0000ff][b]非同次[/b][/color]という。
微分方程式y'=-y+e^2xは1階線形
1.1階線形
[b][size=150]<定数変化法>[/size][/b][br][color=#0000ff]定数変化法は同次方程式の一般解の定数を変数として変化させて、非同次方程式の解を求める方法。[br][/color]たとえば、[b]dy/dx-y=x[/b]はdy/dx=x+yとなり、y/xの式ではないので、同次ではないね。[br]そこでx=0としておきあとで復活させる。[br]・[b]dy/dx=y[/b]。1/y dy=1 dxで変数分離すると、∫1/y dy=∫1 dxによって、log|y|=x+c [br]Cを定数とする一般解は[b]y=Ce[/b][sup][b]x[/b][br][/sup]・このCをxの関数として、c(x)とおき、もとの式に代入しよう。y=c(x)e[sup]x[/sup]とおく。[br]このyを最初の式に入れると、dy/dx-y=(c(x))'e[sup]x[/sup]+c(x)(e[sup]x[/sup])'-c(x)(e[sup]x[/sup])=(c(x))'e[sup]x[/sup]=x。[br]最後の等式を変形して、dc(x)/dx=x/e[sup]x[/sup]=x・e[sup]-x [/sup]。c(x)=∫e[sup]-x [/sup]x dxとなる。[br][b][color=#0000ff]部分積分する。∫Gf = FG- ∫fGとして、[br][/color][/b]f,G=e[sup]-x[/sup],xとするとF,g=-e[sup]-x[/sup],1 から、Fg=-e[sup]-x[/sup]となり積分はe[sup]-x[/sup]だから、c(x)=x・(-e[sup]-x[/sup])-e[sup]-x[/sup]+D。[br]つまり非同次の一般解はy=(x・(-e[sup]-x[/sup])-e[sup]-x[/sup]+D)e[sup]x [/sup][b]y=-x-1+De[/b][sup][b]x[/b][br][/sup][br][b][size=150]<1階線形微分方程式>[/size][/b][br]上と同様にして[b]dy/dx+p(x)y=q(x)[/b]についても、[br]いったんq(x)=0として、∫1/ydy=-∫p(x)dx=r(x)とおくと、(r(x))'=-p(x)となる。[br] log|y|=r(x)+C、Cを定数とする一般解がy=Ce[sup]r(x) [/sup]。C=c(x)として、y=c(x)e[sup]r(x)[br][/sup][b][color=#0000ff]積の微分(FG)'= fG+Fgから、[br][/color][/b]dy/dx+p(x)y=(c'(x)e[sup]r(x)[/sup]+c(x)(e[sup]r(x) [/sup])')+p(x)c(x)e[sup]r(x)[/sup]=q(x) r(x)'=-p(x)によって相殺される部分がある。[br] c'(x)e[sup]r(x)[/sup]=q(x) だから、c(x)=∫ q(x)・e[sup]-r(x)[/sup]dx+D。[br]つまり、[br][b]y=e[sup]r(x)[/sup](∫ q(x)・e[sup]-r(x)[/sup]dx+D)[/b] r(x)=-∫p(x)dxとするとき[br][color=#0000ff](別解)[/color][br][size=200][b]dy/dx+p(x)y=q(x)[/b][br][/size][b][color=#0000ff][size=150]r=∫p(x)dxとおき、両辺にe[sup]r[/sup]をかけると、[br][/size][/color][/b]dy/dx e[sup]r[/sup] + p(x) y e[sup]r[/sup] = q(x) e[sup]r[/sup][br]左辺は[b]積の微分法則を逆算[/b]すると、y' (e[sup]r[/sup]) + y (p(x) e[sup]r[/sup] )=(ye[sup]r [/sup])'[br]だから、(ye[sup]r [/sup])' =q(x) e[sup]r[/sup][br]つまり、ye[sup]r[/sup] = ∫q(x) e[sup]r[/sup] dx+c[br][color=#0000ff][size=200][color=#0000ff][size=200][b]r=∫p(x)dx[/b]とするとき[/size][/color][b]y=1/e[/b][sup]r [/sup][b](∫ q(x)・e[/b][sup]r[/sup][b]dx+c) [br][/b][/size][/color][color=#0000ff][br](例)[br][/color][b]y'+y=e[sup]2x[br][/sup][/b][size=150][size=100]p(x)=1,q(x)=e[sup]2x[/sup]から、∫p(x)dx=∫1dx=xだから、[br]y=1/e[sup]x [/sup](∫e[sup]2x[/sup]e[sup]x[/sup]+c)=1/e[sup]x [/sup](∫e[sup]3x[/sup]+c)=1/e[sup]x [/sup](1/3e[sup]3x[/sup]+c)[br][b]y=1/3e[sup]2x[/sup]+c/e[sup]x [/sup][/b][/size][/size]
微分方程式y'+y = xy^2はベルヌーイ型
微分方程式y'+y = xy^3はベルヌーイ型
2.ベルヌーイ型
[b]ベルヌーイ型は線形1階に似ているけれど、xだけの項の代わりにxだけの項にy[sup]n[/sup]をかけた形[br]dy/dx+p(x)y=q(x)y[sup]n[/sup][/b][br]の微分方程式だ。[br][color=#0000ff]z=y[sup]1-n[/sup]=y/y[sup]n[/sup]と変数変換すると、1/(1-n)dz/dx+p(x)z=q(x)と、1階線形に直せる[/color]。[br][color=#0000ff](理由)[/color][br]合成関数の微分で、dz/dx=dz/dy dy/dx= (y[sup]1-n[/sup]) dy/dx =(1-n)/y[sup]n[/sup] dy/dx[br]dy/dx= 1/(1-n) dz/dx y[sup]n[/sup][br]と変形できる。もとの式に代入すると、[br][b]1/(1-n) dz/dx y[sup]n[/sup]+p(x)y=q(x)y[sup]n[/sup][/b][br]両辺をy[sup]n[/sup]で割る。[br][b]1/(1-n) dz/dx +p(x)z=q(x)[/b][br]これで、zの一階線形に変換できたね。[br][color=#0000ff](例)[/color][br][b]y'+y = xy[sup]2[/sup][br][/b]1-n=-1から、z=y[sup]-1[/sup]とおくと[br]- z' + z =x から、 z' - z =-x から、[br]p(x)=-1, q(x)=-x[br][b]r=∫p(x)dx=[/b][b]∫(-1)dx=-xとおくと、1階線形と部分積分で(integral(e[sup]-x[/sup])=-e[sup]-x[/sup],(-x)'=-1)から、[br]z=[/b][color=#0000ff][b]1/e[sup]r [/sup](∫ q(x)・e[sup]r[/sup]dx+c)[/b]=[/color]1/e[sup]-x [/sup](∫ (-x)・e[sup]-x[/sup]dx+c)=e[sup]x [/sup](∫ (-x)・e[sup]-x [/sup]dx+c)=e[sup]x [/sup]{(-x)(-e[sup]-x[/sup])-∫(-1)(-e[sup]-x[/sup])+D)}[br]z=x+1+e[sup]x[/sup]D=y[sup]-1[/sup][br][b]y=1/(x+1+e[sup]x[/sup]D)[br][/b][color=#0000ff](例)[/color][br][b]y'+y = xy[sup]3[/sup][br][/b]1-n=-2から、z=y[sup]-2[/sup]とおくと[br](-1/2) z' + z =x から、 z' -2 z =-2x から、[br]p(x)=-2, q(x)=-2x[br][b]r=∫p(x)dx=[/b][b]∫(-2)dx=-2xとおくと、1階線形, 部分積分で(integral(e[sup]-2x[/sup])=-1/2e[sup]-2x[/sup],(-2x)'=-2)から、[br]z=[/b][color=#0000ff][b]1/e[sup]r [/sup](∫ q(x)・e[sup]r[/sup]dx+c)[/b]=[/color]1/e[sup]-2x [/sup](∫ (-2x)・e[sup]-2x[/sup]dx+c)=e[sup]2x [/sup]{(-2x)(-1/2e[sup]-2x[/sup])-∫(-2)(-1/2e[sup]-2x[/sup])+D)}[br]=e[sup]2x [/sup]{xe[sup]-2x[/sup]+1/2e[sup]-2x[/sup]+D)}= x + 1/2 + De[sup]2x [/sup]=y[sup]-2[/sup][br][b]y[sup]2[/sup](x+1/2+e[sup]2x[/sup]D)=1[/b]
ロジスティックモデル
3.ロジスティック
指数関数のグラフは時間とともに急激に増大してしまう[br]人口爆発予測の曲線として使われたりする。[br]でも、実際は人口が無限大ということはなく、[br]どこかで頭打ちがあるだろう。[br]それも表せるのが[br][b][color=#0000ff][size=150]ロジスティックモデルだ。[br]y'- Ay=- By[sup]2[/sup](A,Bは正の定数)[br][/size][/color][/b][br]これは、ベルヌーイ型でもあるね。[br]y'-Ay = -By[sup]2[/sup][br]1-n=-1から、z=y[sup]-1[/sup]とおくと[br]- z' -A z =-B から、 z' + Az =B から、[br]p(x)=A, q(x)=B[br][b]r=∫Adx=A[/b][b]xとおくと、1階線形と部分積分で(integral(e[sup]Ax[/sup])=1/Ae[sup]Ax[/sup],(B)'=0)から、[br]z=[/b][color=#0000ff][b]1/e[sup]r [/sup](∫ q(x)・e[sup]r[/sup]dx+c)[/b]=[/color]1/e[sup]Ax [/sup](∫ (B)・e[sup]-Ax[/sup]dx+c)=1/e[sup]Ax [/sup](∫ (B)・e[sup]-Ax [/sup]dx+c)[br]=1/e[sup]Ax[/sup]{(B)(1/Ae[sup]Ax[/sup])-∫(0)(1/Ae[sup]-Ax[/sup])+D)}=1/e[sup]Ax [/sup]{(B/A)e[sup]Ax[/sup]+D}[br]z=(B/A) + D/e[sup]Ax[/sup]=y[sup]-1[/sup][br][color=#0000ff][b][size=150]y=1/(B/A+D/e[sup]Ax[/sup])となるね。[br][/size][/b][/color][br]これは、xが時間、yが人口で[br]B=0なら指数型人口増加のモデルy=(1/D)e[sup]Ax[/sup](Dは正)なる。[br]微分方程式はy'=Ayで、人口増加のスピードdy/dxは、そのときの人口y(x)に比例するというマルサスの法則にあてはまるね。[br]Bが正なら、制御項([b][color=#0000ff][size=150]- By[sup]2[/sup][/size][/color][/b])が効いていて単調に変化して、極限値A/Bに収束する。[br]y(0)がA/Bより少ないときはDが正で単調増加し、y(0)がA/Bより多いときはDが負で単調減少する。[br]
4.実装
[color=#9900ff][b][u][size=150]質問:1階線形微分方程式をsympyで解くにはどうしたらよいでしょうか。[br][/size][/u][/b][/color][br]yが関数であることをy=Function('y')で宣言します。[br][b]y'+y=e[sup]2x[br][/sup][/b][size=150][size=100]は、y'をDerivative(y(x),x)、yをy(x)で、e^2xをexp(2*x)とします。[br]等式なので、eq=Eq(Derivative(y(x),x) +y(x), exp(2*x)と等式自体を変数にしましょう。[br]これをy(x)の陽関数としての微分方程式を解くために[br]dsolve(eq,y(x))としましょう。[br][b]y=1/3e[sup]2x[/sup]+c/e[sup]x [/sup][/b][/size][/size][br]が求められるはずです。[br]#[IN]==========================[br]from sympy.abc import *[br]from sympy import *[br][b]y = Function('y')[br]eq = Eq(Derivative(y(x), x)+y(x), exp(2*x))[br]dsolve(eq, y(x))[br][/b]#[OUT]=========================
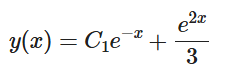
[b]だから、もちろん、ベルヌーイ型でも同じようにできるでしょう。[br]なれてきたら、1行でかけますね。yをy(x)として書くことだけ気をつけよう。[br]y'+y = xy[sup]2[/sup][br][/b][b]y=1/(x+1+e[sup]x[/sup]D)[br][/b][b][color=#0000ff]#[IN]=======================[br]dsolve( Eq(Derivative(y(x), x)+y(x), x*y(x)**2), y(x))[br]#[OUT]=========================[/color][/b]