islamic geometric patterns
For a long time Islamitic decoratif pattern stood as a synonym for ruler and compss constructions and the Alhambra in Granada. An uplifting article in 2007 in Science raised much attention and opened the eyes of the world for Iranian patterns and a different approach, until then only known by specialists. All of a sudden everybody spoke about girih tiles, quasi-crystallyne structures ann Penrose tilings. It also raised many comments by specialists and many interesting articles and books were published. The aim of this GeoGebrabook is to introduce you to this fascinating subject and the work of a number of specialists on it. If you want to discover and investigate muqarnas, see my book on this related issue at [url]https://www.geogebra.org/m/n7ps6rtv[/url].
Table of Contents
- Alhambra
- the Alhambra
- Penrose - crystals - islamic patterns
- decorative patterns
- Maragha - Iran
- pattern and tiles
- girih tiles
- reconstruct the girih pattern (1)
- reconstruct the girih pattern (2)
- Topkapi scroll
- girih tiles and Penrose
- inflation and deflation
- Penrose big and small
- two lectures bu Peter Lu
- Topkapi scroll
- puzzle with girih
- What proceeded - E.H. Hankin
- E.H. Hanking
- Geometric Patterns
- octagons
- decagons and pentagons
- Other tiles
- Peter Cromwell
- From circles to polygons
- (10/3) and (10/4) polygons
- pattern with (10/3) polygons
- patroon with (10/4) polygons
- (10/3) and (10/4) pattern compaired
- other tiles
- octagons - acute
- octagons - median
- octagons - obtuse
- other possibilities
- Hankin
- Friday Mosque in Isfahan
- global look
- angles of the tiles
- angle with the edges
- line pattern
- decorative pattern
- unit repeat
- dual line patterns
- Broadened lines
- dual pattern
- stars with floral motives
- dual pattern with 5-fold symmetry
- Filling in a square
- virtuoso calligraphy
- division
- combining stars
- circles and bundles of radii
- unit repeat
- 12- and 9-pointed stars
- non-systhematic patterns
- 10- and 11-pointed stars
- 13- and 11-pointed stars
- domes
- starting from a dodecahedron
- alternatives
- dome in sectors
- stars and curvature
- Mahan
- Yazd
- Saveh
- Carol Bier
- Carol Bier
- an alternative approach
- Gonbad-e Sork
- Kharraqan 1
- Kharraqan 2
- Nakhchyvan
- comments and arguments
- girih tiles
- Gunbad-e Kabud
- aperiodic patterns
- tympan Darb-i Imam (1)
- tympan Darb-i Imam (2)
- abstract concepts and practice
- division
- Topkapi scroll
- Eric Broug
- 5-fold system
- Jay Bonner
- extra
- links
the Alhambra
Symmetry groups
Marcus du Sautoy calls the Alhambra ‘the palace of symmetry' and describes how he walks through the Alhambra with his son and a list of wallpaper groups. The people who decorated the 14th century weren’t aware of a theoretical concept of 17 possible groups but they managed to apply them all. Room after[br]room, wall after wall they surprize the visitor with just a new variation, establishing another pattern.
unit repeat
De Islamic decorators knew which regular forms to use to create tilings and used squares, rhombuses, parallelograms, triangles and hexagons as unit repeats. They created tilings using all kinds on transformations on this unit repeat.
GeoGebrabooks
I created some GeoGebrabooks in dutch on the Alhambra: [br]- [url=https://ggbm.at/cwdEuhUw]symmetrie in het Alhambra[/url] [br]- [url=https://ggbm.at/VN5CGgXQ]behangpapiergroepen[/url] (wallpapergroups)[br]- [url=https://ggbm.at/acq9cpp3]Alhambra met passer, lineaal en GeoGebra[/url] [br]- [url=https://ggbm.at/M4BJvN9m]Escher en het Alhambra[/url]
decorative patterns
2007
In march 2007 Peter J. Lu (Harvard) and Paul J. Steinhardt (Princeton) published a remarkable article in Science titled “[url=https://www.researchgate.net/publication/6484358_Decagonal_and_QuasiCrystalline_Tilings_in_Medieval_Islamic_Architecture]decagonal and Quasicrystalline Tilings in Medieva Islamic Architecture[/url]”.
straightedge and compass
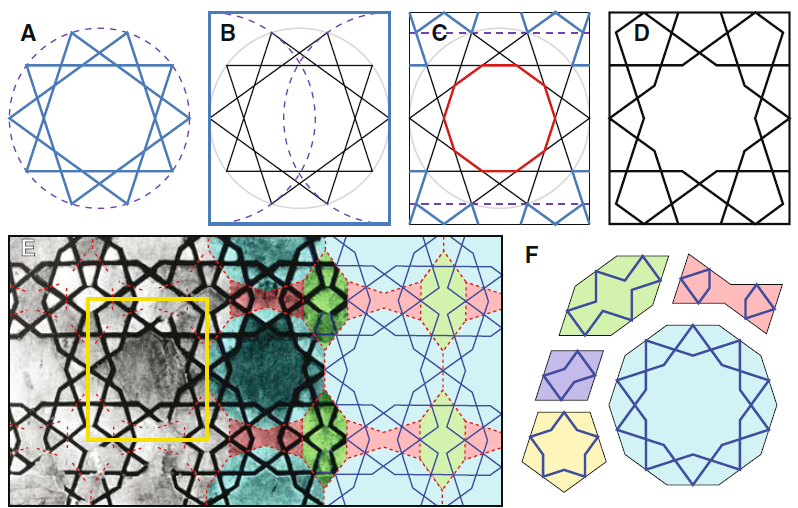
The conventional view holds that the patterns in Islamic architecture were drafted with a straightedge and a compass. In pictures [b]A [/b]to [b]D[/b] you can see such a construction starting from a ten pointed star.
The autors suggest that by 1200 AD a breakthrough occured in which a set of tiles were used to conceive the tesselations. [br]Picture [b]E[/b] shows on the right how the same pattern is constructed, just by the placement of these tiles, decorated with zigzagging lines. These tiles are named girih tiles, after the Persian word for 'knot'. Girih tiles are easy in use and give the decorators great freedom in conceaving apparently complex tilings.[br]Picture [b]F[/b] shows the 5 tiles and their decorative pattern of lines.[br][br][u]Note[/u]: Specialists write that designers knew this system much earlier than 1200. They even assume this[br]system, together with ruler and compass constructions was in use from the start, gradually becoming the most used system. The system has been already reported in the Western world by E.H. Hankin in 1925. Finally the set of polygons mentioned by Lu en Steinhardt wasn’t the only existing set.
E.H. Hanking
Ernest Hanbury Hanking (1865 - 1939) was a British biologist working in colonial British-India. Apart of his studying on diseases as malaria and cholera he was also interested in Islamic patterns on the monuments of Mogul emperors from the 15th until the 18th century.
Taj Mahal
The Taj Mahal, the mausoleum built by emperor Sjah Jehan between 1632 and 1648 for his deceased wife is not only the most famous of these mogul monuments but one of the most famous in the world. The walls of the monuments are decorated with floral motives, but it was another type of decoration in which Hanking was interested.
Fatehpur Sikri
As a scientist Hanking was fascinated by the geometric patterns he found[br]in Fatehpur Sikri, the ceremonial city emperor Akbar built. It was the capital of[br]the Mogul empire from 1571 until 1585, when it was abandoned for unknown[br]reasons.
From circles to polygons
In his article [url=http://www.fisme.science.uu.nl/nwd/nwd2009/handouts/tom/Islamic%205%20fold.pdf]The Search of Quasi-Periodicity on 5-Fold Islamic Ornament[/url] from 2009 Peter R. Cromwell describes the transition from a rhombic line pattern with tangent circles to the 'Polygons in Contact' (PIC) of Hankin. Many early Islamitic patterns show a square or triangle grid in which 6-, 8- or 12-pointed[br]star patterns are created. Cromwell illustrates how to create 10-pointed stars upon a rhombic grid with 72° and 108° angles.
[list][*]Draw tangent circles in the rhombic grid centred at the gridpoints.[/*][*]Draw a 10-pointed star whose points coincide with the tangent points of the circles. Some points of the star don’t touch another circle.[/*][*]Draw regular decagons within the circles who’s edges are perpendicular to the points of the star. [/*][*]Substitute the circles by the tangent decagons and hide the rhombic grid[/*][*]Reproduce the star pattern in al circles. In between the decagons bowtie like polygons appear.[/*][*]Extend the lines that define the star into the bow ties until they intersect. In the bow ties appear, congruent with those in the stars.[/*][*]Hide the grid.[/*][/list][br]According to Cromwell the transition from circles to polygons seems small but in fact it isn’t because it allows generalisations with less constraints for the designers. With the ability to combine polygons freely more patterns and star forms can be created. What’s important is the angle between the lines and the edges of the polygons.[br]
octagons - acute
A very classic pattern can be created by combining regular octagons and squares. One can create star patterns by connecting the midpoints of the edges of the octagons. The choice which points are connected defines the resulting pattern. Authors created notation systems for this. The applet below shows so-called 8/3 stars. In them one starts counting from a midpoint of an edge to connect it with the midpoint of the 3rd edge. One con also define the pattern by the angle these line make with the edge. This pattern is called[br]acute. The two lines in the midpoints of each edge make an angle of 45°. In the median system the angle is 90°, in the obtuse 135°.
Broadened lines
In next applet you can see a tiling with 4-fold symmetry, built up with three figures: a regular octagon, a 4-pointed star and a bow tie. Octagons and bow tie are filled in by floral motives, while the lines are broadened and filled in with a geometric pattern.
circles and bundles of radii
starting with radii
The girih method working with a fixed set of polygons creates stars with a fixed number of points. I addition to this system a second method was established. In circle bundles of radii were drawn. Intersection points of these radii define segments, forming polygons. This construction method allows combining stars with a different number of points within one pattern. In the article [url=https://www.nexusjournal.com/volume-18/volume-18-number-1-2016.html]Girih for Domes: Analysis of Three Iranian Domes[/url] the authors Mohammad Hossein Kasraei, Yahya Nourian and Mohamadjavad Mahdavinejad describe this method as the radial girih method or [b][i]Dast-Gardan girih[/i][/b].[br][br][br]
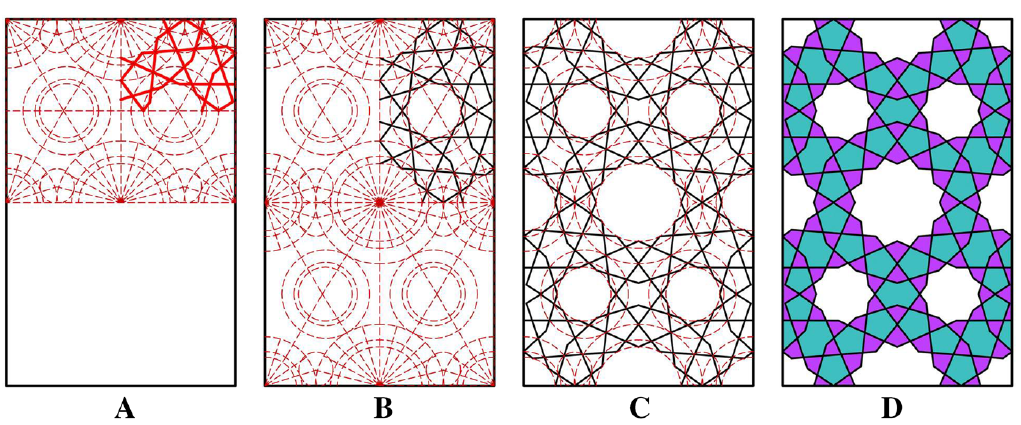
In the example you can see how the pattern is constructed. [list][*]Within a unit repeat concentric circles are drawn on every corner point.[/*][*]These circles are divided into congruent sectors.[/*][*]Diagonals in the unit repeat define the center points of additional circles [b][i](step A)[/i][/b].[/*][*]Connecting intersection points of radii and circles generates a line pattern [b][i](step B)[/i][/b].[/*][*]This pattern is mirrored on the axes of symmetry if the unit repeat [b][i](step C)[/i][/b].[/*][/list]The result [b][i](step D)[/i][/b] is a geometric pattern that combines 12-pointed stars with 9-pointed stars.
A nice example is shown in a drawing by Aslam Qureshi.[br]The construction starts with two quart circles in opposed corners of a rectangle and smaller, tangent circles. With bundles of radii and intersections points a balanced 7-fold pattern is created.
starting from a dodecahedron
In a plane it’s not possible to realise a tiling only with regular pentagons. But in space it’s possible to create a dodecahedron with 12 regular pentagons.[br]On the faces of it one can create line patterns the same way as in a plane. If you project this pattern on the circumscribed sphere the result is a line pattern one can use for a domed structure. This principle was used for the north-eastern dome of the Friday Mosque in Isfahan (1088-89).
Carol Bier
Who's counting?
In [url=https://archive.bridgesmathart.org/2011/bridges2011-497.pdf]Taking Sides, but who's counting?[/url] Carol Bier pleads for a critical multi-disciplinary view in the examination of medieval Islamitic decorative pattern. She writes that Lu & Steinhardt Makovicky and Bonner pay a lot of attention for the tilings with 10-fold symmetry and the underlying polygonal pattern, but miss the fact that the building itself is decagonal and not octagonal, uncritically following the errors of earlier publications. She publishes a historical photograph and a drawing of the plan, both from 1937, clearly showing the shrine is decagonal, which she points out is crucial for the understanding of the building.
Picture of the Gunbad-e Kabud by M.B. Smith taken the 4th of august 1937.[br]Plan of the Gunbad-e Kabud drawn by M.B. Smith dated the 6th of august 1937.
a global view
Carol Bier strongly pleads for an global view on the building. Modern researchers tend to project their mathematical story of quasi-crystalline structures on the medieval decorations and easily forget the historical-cultural background.[br]In [url=https://works.bepress.com/carol_bier/38]The Decagonal Tomb Tower of Maragha and its Architectural Context[/url] she tries to situate the building within a broader historical background. Very interesting too is her article: [url=https://works.bepress.com/carol_bier/86/]Geometry Made Manifest: Reorienting the Historiography of Ornament on the Iranian Plateau and beyond[/url]. In this article she focusses on the link between the geometric pattern and the religious texts which are not accidently chosen. The[br]Kuran texts deal with the visible and invisible and about perfection. Our Western figurative view tells us the patterns aren’t representing anything, they’re just ‘ornamental’. According to her a Kuran fragment surah 59, verses 21-21 isn’t coincidently chosen: [i]"...These are the examples (patterns) we present to the people; perhaps they will give thought. He is Allah; other than whom there is no deity, knower of the unseen and the witnessed.." . [/i]The geometric patterns to contain visible and unseen lines and lots of texts connect the study of geometry with learning and understanding deeper insights. Lots of material you can find in online published articles. At the end of this GeoGebrabook you can find a selection of [url=https://www.geogebra.org/m/cyjb6gsb#material/vprvyw3j]links[/url].
timpaan op de Gonbad-e Sork (Maragha)
from Seljuks to Mongols
It’s accepted that the Gunbad-e Kabud dates from 1196-97 AC following a long line of Seljuk experiments shortly before the Mongol invasion in Iran, starting in 1219. Maragha was conquered in 1221. After further conquests Hulegu Khan, grandson of Dzjangis Khan, returned to Maragha making it the capital if the Ilkhanate. He built an astronomical observatory attracting the brightest scientists. After the conquest of Bagdad Hulegu even transferred the scientific library of Bagdad to Maragha. New instruments were developed and used and Maragha became a motor for scientific development. The remarkable building with its (unusual) decagonal plan and its decorative patterns marks as well the endpoint of the Seljuk experiments as the beginning of new developments under the new rulers, as a centre with a concentration of scientific knowledge and background.[br]
Not just the wall panels
Carol Bier not just describes the wall panels, but also focusses on the tympans and spandrels above the wall panels. In the upper spandrel she distinguishes three superposed line patterns that mark 5-, 6- and 7-pointed stars.
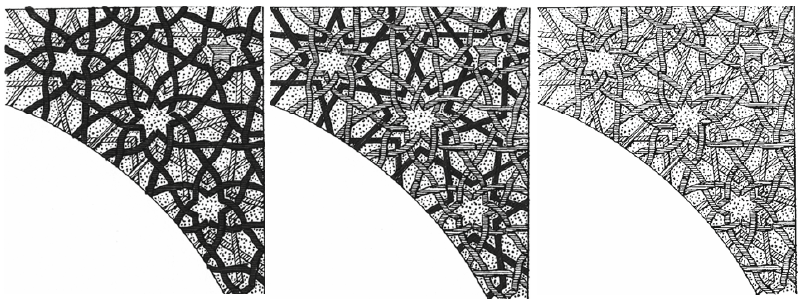
Drawings from the article of Carol Bier:[br]The Decagonal Tomb Tower at Maragha and its Architectural Context
In the lower spandrels, around muquarnas you can[br]notice (partly) overlapping polygons with inscribed stars: from top to the[br]bottom a 8-, 9- and 10-pointed star.
Click on the checkboxes to discover the stars
Lecture of Carol Bier in the Metropolitan Museum of Arts in New York
Online
More links you can find at [url=https://works.bepress.com/carol_bier/]https://works.bepress.com/carol_bier/[/url]
girih tiles
help or crucial?
Wat was the role girih tiles played? Hankin mentioned them first in the Western world but places them as an aid in the use of so called 'strapwork' that uses rule and compass for constructions. Lu and Steinhardt argument that the use of the tiles played a crucial role in the construction itself. The opinion of specialists differs.
Hogendijk
Hogendijk is critical and argues only one text remains that explains how a certain drawing is to be constructed. As in the drawings of the Topkapi scroll the lines of the girih tiles are visible, but this text explains how to create it. He continues: [i]"In the mosaic in the Friday Mosque of Isfahan the girih tiles aren’t visible and it is clear that they didn’t play a role in the production process. This is to say that it weren’t the girih tiles that were fabricated (cut out or baked) and matched to create the pattern. This means that the tiles belong to the design phase."[/i]
Cromwell and Bonner
Cromwell quotes Bonner: [i]"Bonner argues the PIC (the Polygons in Contact of Hankin) is the only system with historical proof that it was used by designers throughout the Islam world."[/i]
Lu and Steinhardt
"The use of girih tiles has practical advantages and allows easier,[br]faster and more correct realisations by workers who weren’t familiar with their[br]mathematical properties. More, they prevent the accumulation of distortions you[br]can expect while drawing manually with ruler and compass. More, girih tiles[br]allow to create constructions that are very difficult to construct by strapwork.[br]Starting from 1200 AC patterns of this type appear on Seljuk buildings.