Surface area of a Right Circular Cylinder (MA5-ARE-C-01)

Introduction

In this activity, we will get familiar with the geometry of a [b]right circular cylinder[/b]. This is a long name that we will explain. It describes [b]a particular type of cylinders[/b]: the most common one! For instance, we find it inside kitchen-rolls and toilet paper rolls. As this is the only type of cylinders we will encounter in high school, we commonly just use "[b]cylinder[/b]".[br][br][i][b]Credit:[/b][/i] This activity was originally developed by [i][b]wheelerELHS.[/b][/i][br]

Instructions

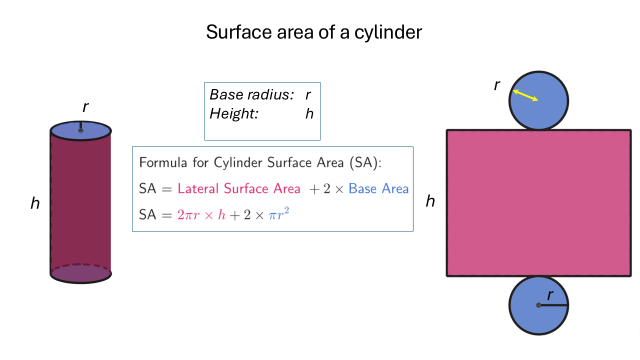
[br]Adjust the [i][b]radius (r)[/b][/i] and [i][b]height (h)[/b][/i] to observe the changes to the [b]cylinder [/b]and its [b]net[/b].[br][br]The [b]surface area of the cylinder[/b] is the [b]sum[/b] of the [b]surface area of the lateral face[/b] and [b]twice[/b] the [b]area of the circular base[/b].[br][br][math]SA=\left(2\pi\times r\times h\right)+2\times\left(\pi\times r^2\right)[/math]

Right circular cylinder

Where does the name come from?

Select [b]all[/b] correct answers.[br][br][br]1) This 3D surface is classified as a cylinder, because.....

the 3D surface has one circular base and one vertex/peak the 3D surface has two parallel circular bases the 3D surface has two parallel polygonal bases the 3D surface has one polygonal base and one vertex/peak

2) This cylinder is a [b]right circular cylinder[/b] because....

the lateral face is perpendicular to the base the lateral face is a rectangle the base is a rectangle the base is circular

3) Is the height of the lateral face of a cylinder related to any of its base's dimensions?

Yes, they are related because the circumference of the base is equal to the height of the lateral face. No, they aren't related because the base and the lateral face can have any dimension independently from each other. No, they aren't related as when the height [i]h[/i] of the lateral face varies the base doesn't change. Yes, they are related because the area of the circular base varies with the height of the lateral face.

4) Is the width of the lateral face of a cylinder related to its base?

Yes, they are related because the circumference of the base is equal to the width of the lateral face. Yes, they are related because the area of the circular base varies with the height of the lateral face. No, they aren't related because the base and the lateral face can have any dimensions independently form each other. No, they aren't related as when the height [i]h[/i] of the lateral face varies the base doesn't change.

Dimensions of this cylinder

Use the sliding bars of the applet to change the dimensions of the cylinder to answer the following questions. [br]You don't need a calculator to answer any of these questions.[br]Select [b]all[/b] correct statements.[br][br]5) Using the sliding bar for the radius of the base, I observe that ...[br]

The smallest value r can be set to is 0.1 The smallest value r can be set to is 0 The biggest value r can be set to is 1.25 The biggest value r can be set to is 3.0

6) Using the sliding bar for the height [i]h[/i] of the cylinder, I observe that ...[br]

The biggest value [i]h[/i] can be set to is 3.0 The smallest value [i]h[/i] can be set to is 0 The biggest value [i]h[/i] can be set to is 1.25 The smallest value [i]h[/i] can be set to is 0.1

7) The smallest possible area of its base is ...

[math]0.0[/math] [math]0.1\times\pi[/math] [math]0.01\times\pi[/math] [math]0.02\times\pi[/math] [math]0.04\times\pi[/math]

8) The smallest possible area of its lateral face is ...

[math]0.0[/math] [math]0.02\times\pi[/math] [math]0.1\times\pi[/math] [math]0.04\times\pi[/math] [math]0.01\times\pi[/math]

9) The smallest possible [b]total area surface[/b] of this cylinder is ...

[math]0.02\times\pi[/math] [math]0.01\times\pi[/math] [math]0.0[/math] [math]0.04\times\pi[/math] [math]0.1\times\pi[/math]

10) What is the surface area of a cylinder with a radius of 1 and a height of 3?

[math]7\times\pi[/math] [math]9\times\pi[/math] [math]8\times\pi[/math] [math]6\times\pi[/math]

10) What is the surface area of a cylinder with a radius of 2 and a height of 0.5?

[math]12\times\pi[/math] [math]6\times\pi[/math] [math]10\times\pi[/math] [math]8\times\pi[/math]

11) If the height of this cylinder is 1, for which value of the base radius [i][b]r[/b][/i] is the [b]lateral area[/b] equal to the [b]area of one of the base[/b]?

[i]r[/i] = 1/2 [i]r[/i] = 1 [i]r[/i] = 2 [i]r[/i] = 3

12) If the height of this cylinder is 1, for which value of the base radius [i][b]r[/b][/i] is the [b]lateral area[/b] equal to the [b]sum[/b] [b]of the base areas[/b]?

[i]r[/i] = 3 [i]r[/i] = 2 [i]r[/i] = 1/2 [i]r[/i] = 1

13) If the height of this cylinder is 2, for which value of the base radius [i][b]r[/b][/i] is the [b]lateral area[/b] equal to the [b]sum[/b] [b]of the base areas[/b]?

[i]r[/i] = 1 [i]r[/i] = 3 [i]r[/i] = 2 [i]r[/i] = 1/2

14) If the height of this cylinder is 2, for which value of the base radius [i][b]r[/b][/i] is the [b]lateral area[/b] equal to the [b]sum[/b] [b]of the base areas[/b]?

[i]r[/i] = 3 [i]r[/i] = 2 [i]r[/i] = 1/2 [i]r[/i] = 1

15) what is the relation between the base radius and the height of the cylinder for which the lateral area and the sum of its base areas (top and bottom) are the same?

[math]r=h[/math] [math]r=h\times\pi[/math] [math]r=2\times h[/math] [math]r=\frac{h}{2}[/math] [math]r=\frac{h}{\pi}[/math]

Practice using the formula

Use the formula and a calculator to calculate the (total) surface area of these cylinders.

16) What is the total surface area ([b]TSA[/b]) of a cylinder of height 3m and base radius 2m? All results are given in squared meters and rounded to one decimal place.

24.0 62.8 37.7 88.0 50.3 20.0

17) Select all answers equivalent to 7.56 [math]m^2[/math].

75600 [math]\text{ }cm^2[/math] 75.6 [math]cm^2[/math] 756 [math]cm^2[/math] 7560 [math]cm^2[/math]

18) What is the total surface area ([b]TSA[/b]) of a cylindrical gutter pipe that is 6 meter long and has a diameter of 10 cm? The result is rounded to a whole number.

[math]\text{18850}cm^2[/math] [math]1005cm^2[/math] [math]19007cm^2[/math] [math]19m^2[/math]

19) A gas pipe with outside diameter of 32 mm is 10 m long. What is its surface area? Choose the closest answer:

[math]1.007m^2[/math] [math]\text{10070}cm^2[/math] [math]100.7cm^2[/math] [math]100700mm^2[/math] [math]1007cm^2[/math]

20) A 1m long section of an optical fibre cable has diameter of 50 micrometre. This section can be seen as a long and very thin cylinder. What is the ratio of the lateral area to the area of one base? Choose the closest answer:

400000 8000 40000 4000 80000