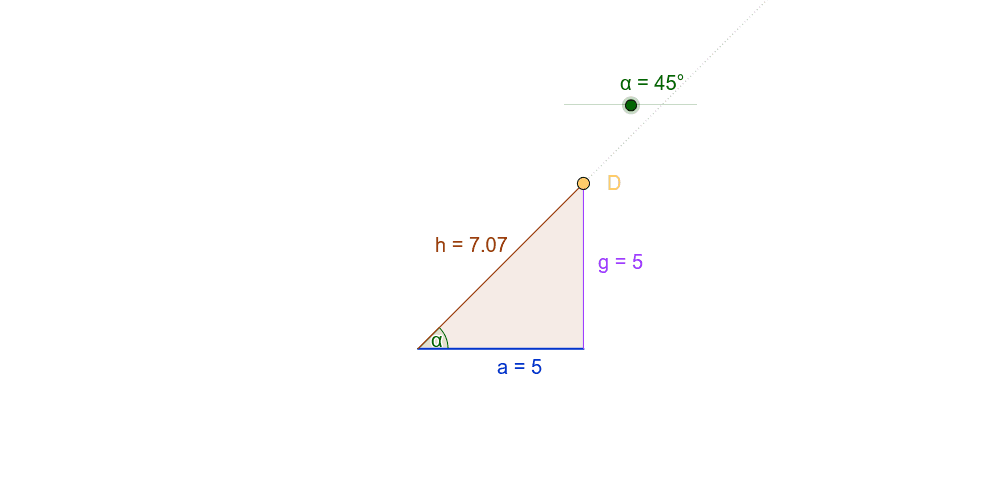
[b]Forschungsauftrag 1: Dynamische Entdeckungen rechtwinkliger Dreiecke (Kleingruppenarbeit, ca. 20 Minuten)[/b][br]---------------------------------------------------------------------------------------------------------[br]I[size=85]n dem folgenden Applet siehst du[br][list][*]ein rechtwinkliges Dreieck mit dem [color=#f1c232]Eckpunkte [b]D[/b][/color], der [b][color=#660000]Hypotenuse h [/color][/b]und der [b][color=#0000ff]Katheten a[/color][/b] und der[color=#9900ff] [/color][b][color=#9900ff]Kathete g.[/color][color=#0000ff] [/color][/b][/*][*]einen [b][color=#38761d]Schieberegler[/color][/b] für den Winkel[color=#9900ff][b] [math]\alpha[/math][/b][/color][color=#9900ff].[/color] Den Winkel  [math]\alpha[/math] kannst du ändern, indem du an dem Schieberegler ziehst. Der Schieberegler durchläuft die Zahlen k [math]\in[/math][0;90]. [/*][/list][/size]---------------------------------------------------------------------------------------------------------[br][br][size=100][i][b]Leite[/b][/i] den Zusammenhang zwischen dem spitzen Winkel [math]\alpha[/math] und den Seitenlängen im rechtwinkligen Dreieck [b]her. [/b]Gehe dazu wie folgt vor: [/size][br][br][u][i]Schritt 1 - Tabelle 1 auf M1: [/i][math]\alpha[/math][/u]= 45° [br][b][i]a) Berechne[/i][/b] die Seitenverhältnisse [math]\frac{g}{h}[/math] und [math]\frac{a}{h}[/math] für das vorgegebene Dreieck mit [math]\alpha[/math] = 45°. [br][b][i]b) Bewege den [color=#f1c232]Punkt D[/color][/i][/b] und [b][i]berechne[/i][/b] erneut die Seitenverhältnisse.[br][b][i]c) Wiederhole[/i][/b] dieses Vorgehen ein weiteres Mal.[br][b][i][br]Notiere[/i][/b] die Seitenlängen und Seitenverhältnisse in der Tabelle 1 auf M1. [br][b][i]Beschreibt[/i][/b] eure Beobachtungen in Stichpunkten. [br][br][u][i]Schritt 2- Tabelle 2 auf M1:[/i] [/u][br]a) [b][i]Verändere[/i][/b] den [color=#38761d]Winkel [/color][math]\alpha[/math] und notiere die Winkelgröße in die Tabelle 2 auf M1. [br]b) [b][i]Wiederhole[/i][/b] den Schritt 1 mit dem neuen Winkel [math]\alpha[/math].[br][br][br]S[i][u]chritt 3 - Tabelle 3 auf M1: [/u][/i][br]a) [b][i]Verändere[/i][/b] erneut den [color=#38761d]Winkel [/color][math]\alpha[/math] und notiere die Winkelgröße in die Tabelle 3 auf M1. [br]b) [b][i]Wiederhole[/i][/b] den Schritt 1 mit dem neuen Winkel [math]\alpha[/math][br][br][br][i][u]Schritt 4: [/u][/i][br][b][i]Fasst[/i][/b] eure Vermutungen über den Zusammenhang zwischen dem spitzen Winkel [math]\alpha[/math] und den Seitenlängen im rechtwinkligen Dreieck in einem Satz [b][i]zusammen[/i][/b]. [br][br][br]

[b][i]Bewege[/i][/b] den Punkt auf dem Einheitskreis. [b][i]Beschreibe[/i][/b] den Zusammenhang zwischen Bogenmaß und Gradmaß. [br]

[i][color=#0000ff]Jetzt wird genau hingeschaut![br][/color][/i][br]---------------------------------------------------------------------------------------------------------[br]I[size=85]n dem folgenden Applet [b][i]siehst du [/i][/b][br][list][*]den [b]Einheitskreis[/b] mit dem Radius 1 und dem Mittelpunkt (0;0)[/*][*]einen [b][color=#3c78d8]Schieberegler[/color][/b][color=#6fa8dc] [/color]für den [color=#3c78d8]Winkel in Bogenmaß b[/color][color=#6d9eeb] [/color]bzw.[color=#3c78d8] [/color][color=#3c78d8][b]in Gradmaß [math]\alpha[/math][/b][/color][color=#9900ff].[/color] Den Winkel kannst du ändern, indem du an dem Schieberegler ziehst. Der Schieberegler durchläuft die Zahlen b[color=#3c78d8] [/color][math]\in[/math][color=#3c78d8][[/color][math]-2\cdot\pi[/math][color=#3c78d8] ; [/color][math]6\cdot\pi[/math][color=#3c78d8]][/color] bzw.[color=#3c78d8] [/color][math]\alpha[/math][math]\in[/math][color=#3c78d8][[/color][math]-360^{\circ};1080^{\circ}[/math][color=#3c78d8]][/color][/*][*]zu jedem [b][color=#3c78d8]Winkel[/color][color=#6d9eeb] [/color][/b]den zugehörigen [color=#ff0000][b]Sinuswert[/b][/color] am Einheitskreis[/*][/list][i][b]Veränderst[/b][/i] du den Winkel mithilfe des Schiebereglers, so entsteht punktweise der [color=#9900ff][b]Graph der Sinusfunktion[/b][/color].[br][/size][br]---------------------------------------------------------------------------------------------------------[br][br][size=100][b][i]Leite[/i] [/b]mindestens 4 Eigenschaften der Sinusfunktion [i][b]her[/b], [/i]indem du das Applet [u]möglichst genau [/u][i][b]untersuchst[/b][/i]. [br][br][b][i]Halte[/i][/b] deine Beobachtungen in geeigneten Darstellungsformen auf dem M1 und M2 [b][i]fest.[/i][/b][br][size=85](zum Beispiel in Form von stichpunktartigen Beschreibungen, Skizze, Tabelle, Graph...)[/size][br][br][color=#6aa84f]Hinweis:[/color] [br][/size][size=100]Brauchst du Denkanstöße? In dem Umschlag auf deinem Platz findest du [u]Tippkarten[/u]. [/size]

______________________________________________________________________________________________________________________________________________________________________________________________________________________________

______________________________________________________________________________________________________________________________________________________________________________________________________________________________

[i][b][right][/right]Bereite[/b][/i] dich darauf [i][b]vor[/b][/i], deinen Mitschüler:innen die von dir hergeleiteten Eigenschaften der Sinusfunktion zu [i][b]präsentieren[/b][/i]. Verwende zur Präsentation das Applet.

______________________________________________________________________________________________________________________________________________________________________________________________________________________________

[b][i]Schon fertig?[/i][/b] [br][br]Dann hole dir am Pult die Sprinteraufgabe ab und [b][i]bearbeite[/i][/b] diese mit deinen Lernpartner:innen