Images. Finding Geometric Medians on a bounded area
[size=85] Let Pi=(xi,yi,zi) n moving points in ℝ³ (lP:={P1,P2,...,Pn}). I want to find the points P=(x,y,z) on the surface of the sphere -S (radius R) that are critical (relative min/max or saddle points at (x,y,z)) of a function f(x,y,z):=-sum of the distances from P to the all points from lP. Critical points can be found using Lagrange multipliersas finding the Extreme values of the function f(x,y,z) subject to a constraining equation g(x,y,z):=x[sup]2[/sup]+y[sup]2[/sup]+z[sup]2[/sup]-R[sup]2[/sup]=0. There is a system of equations: ∇f(x,y,z)= λ∇g(x,y,z). A local optimum occurs when ∇f(x,y,z) and ∇g(x,y,z) are parallel, and so ∇f is some multiple of ∇g. [br] This applet illustrates distributions of geometric medians on a sphere of radius R "induced" by a discrete sample of moving points in three-dimensional space.[br]Description in [url=https://www.geogebra.org/m/y8dnkeuu]https://www.geogebra.org/m/y8dnkeuu[/url][br]Applets: [br][url=https://www.geogebra.org/m/bm76gdkb]Example[/url] of Applet in which 3 moving points in three-dimensional space "induce" 8 geometric medians on a sphere. [br][url=https://www.geogebra.org/m/avps5da6]Example[/url] of Applet in which 6 moving points in three-dimensional space "induce" 14 geometric medians on a sphere.[/size][br]

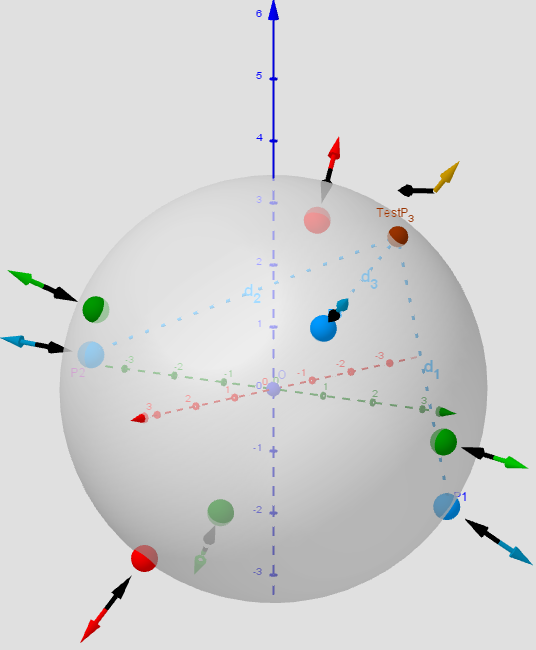
[size=85]Distribution of points P[sub]i, [/sub][color=#5b0f00]test Point[/color][sub], [/sub] [color=#ff0000]Max[/color]/[color=#0000ff]min[/color]/[color=#38761d]saddle[/color] -[color=#333333]Critical points[/color] on a sphere. Vectors ∇f and ∇g at these points. n=3.[/size]
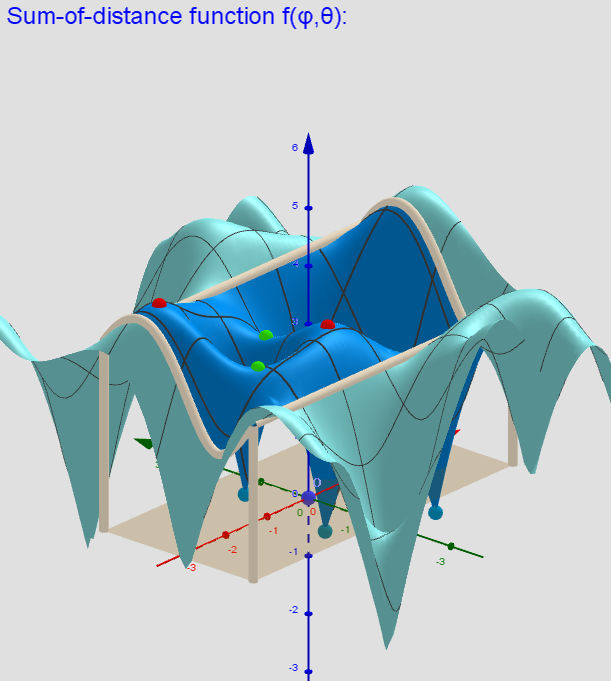
[size=85]Two-variable function f(φ,θ) over a rectangular region: - π ≤φ ≤ π; -π/2≤θ≤π/2. n=3.[/size]
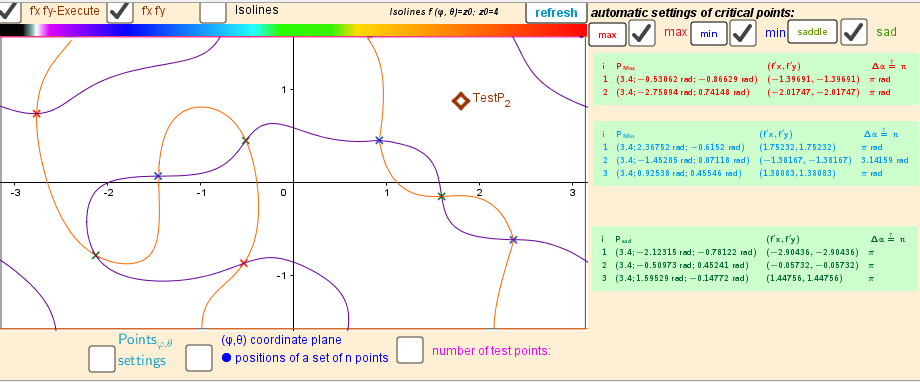
[size=85]Intersection points of implicit functions -solutions of the Lagrange equation. n=3[/size]
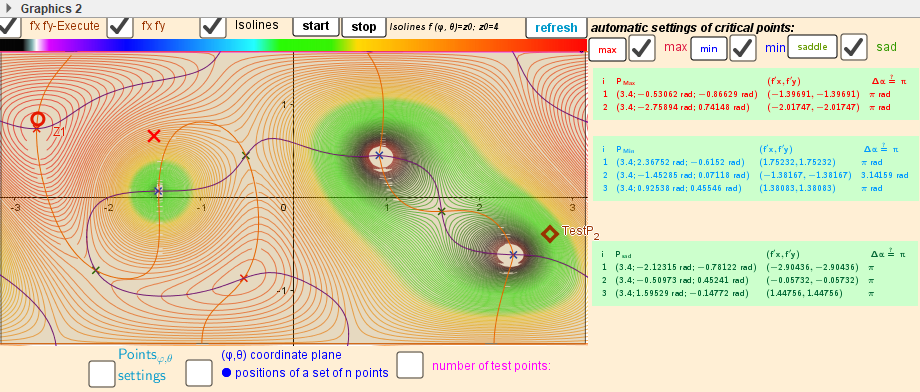
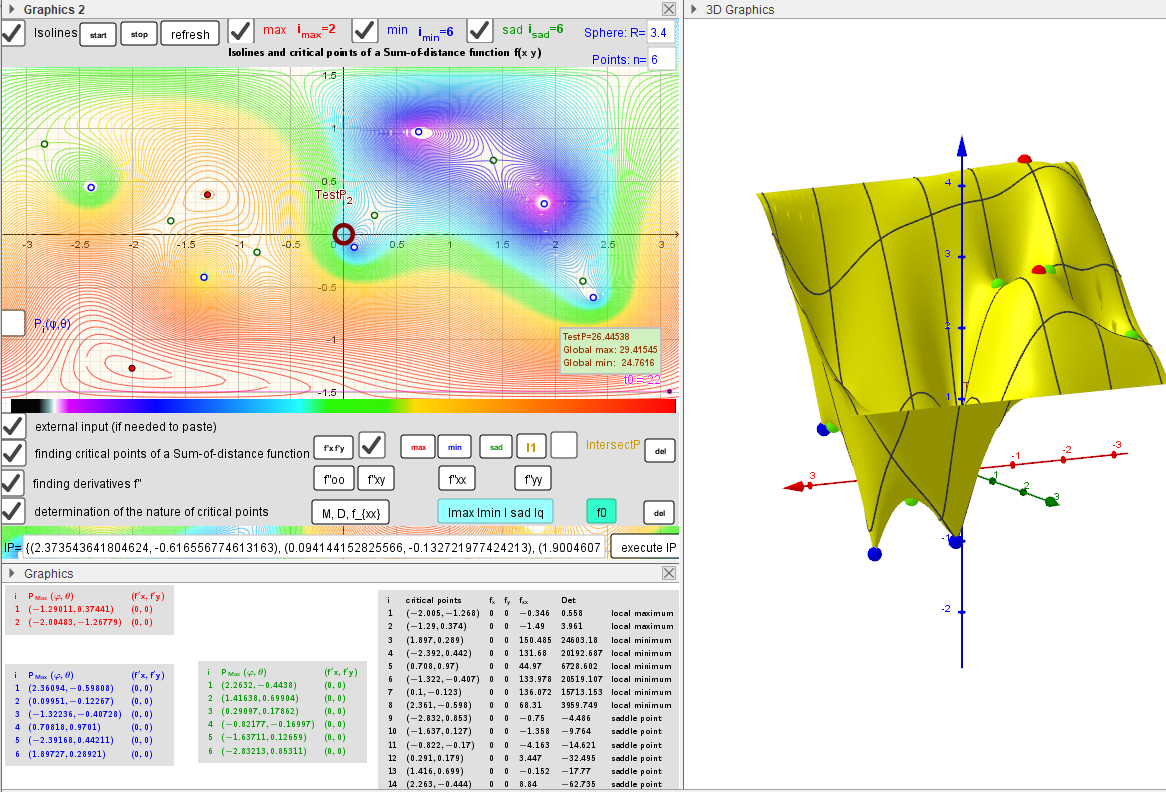
I[size=85]solines around critical points. n=3.[/size]
Isolines and Intersection Implicit Curves f'φ(φ, θ)=0 f'θ(φ,θ)=0 over a rectangular region [-π,π],[-0.5π,0.5π]. n=6.
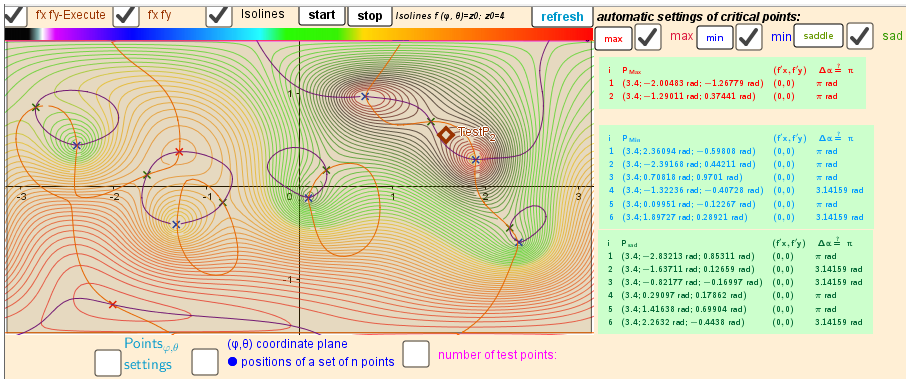
Critical points as Geometric Medians and their nature using hessian matrix.