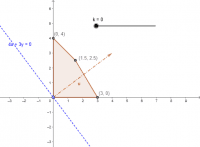
Maximizar [math]4x+3y[/math][br]sujeta a [math]x+y\le4[/math][br] [math]5x+3y\le15[/math][br] [math]x,y\ge0[/math][br]Graficamos la región factible. El deslizador [math]k[/math] mostrará distintas curvas de nivel (hiperplanos) de la función objetivo [math]z=4x+3y[/math]. Movemos el deslizador en la dirección del vector gradiente (en rojo), [b]c [/b]= (4 3), hasta alcanzar un punto óptimo.

Se observa que se alcanza el valor óptimo en [math]x=\frac{3}{2}[/math], [math]y=\frac{5}{2}[/math] y este valor óptimo es de [math]z=13.5=\frac{27}{2}[/math].