-
Funciones
-
1. Carácterísticas de la gráfica
- Características de la gráfica de una función
- Tasa de variación media
- Dominio y recorrido en una función definida a trozos
-
2. Funciones algebraicas
- Funciones cuadráticas
- Función de propocionalidad inversa
- Funciones radicales
-
3. Funciones logarítmica y exponencial
- Dominio y Recorrido de una función logarítmica
- Dominio y Recorrido de una función exponencial
- LOGARITMO Y EXPONENCIAL
- Función exponencial
-
4. Funciones trigonométricas
- Rubber Pencil Illusion
This activity is also part of one or more other Books. Modifications will be visible in all these Books. Do you want to modify the original activity or create your own copy for this Book instead?
This activity was created by '{$1}'. Do you want to modify the original activity or create your own copy instead?
This activity was created by '{$1}' and you lack the permission to edit it. Do you want to create your own copy instead and add it to the book?
Funciones
Ana Belén Álvarez Heredia, Oct 25, 2014
Table of Contents
- Carácterísticas de la gráfica
- Características de la gráfica de una función
- Tasa de variación media
- Dominio y recorrido en una función definida a trozos
- Funciones algebraicas
- Funciones cuadráticas
- Función de propocionalidad inversa
- Funciones radicales
- Funciones logarítmica y exponencial
- Dominio y Recorrido de una función logarítmica
- Dominio y Recorrido de una función exponencial
- LOGARITMO Y EXPONENCIAL
- Función exponencial
- Funciones trigonométricas
- Rubber Pencil Illusion
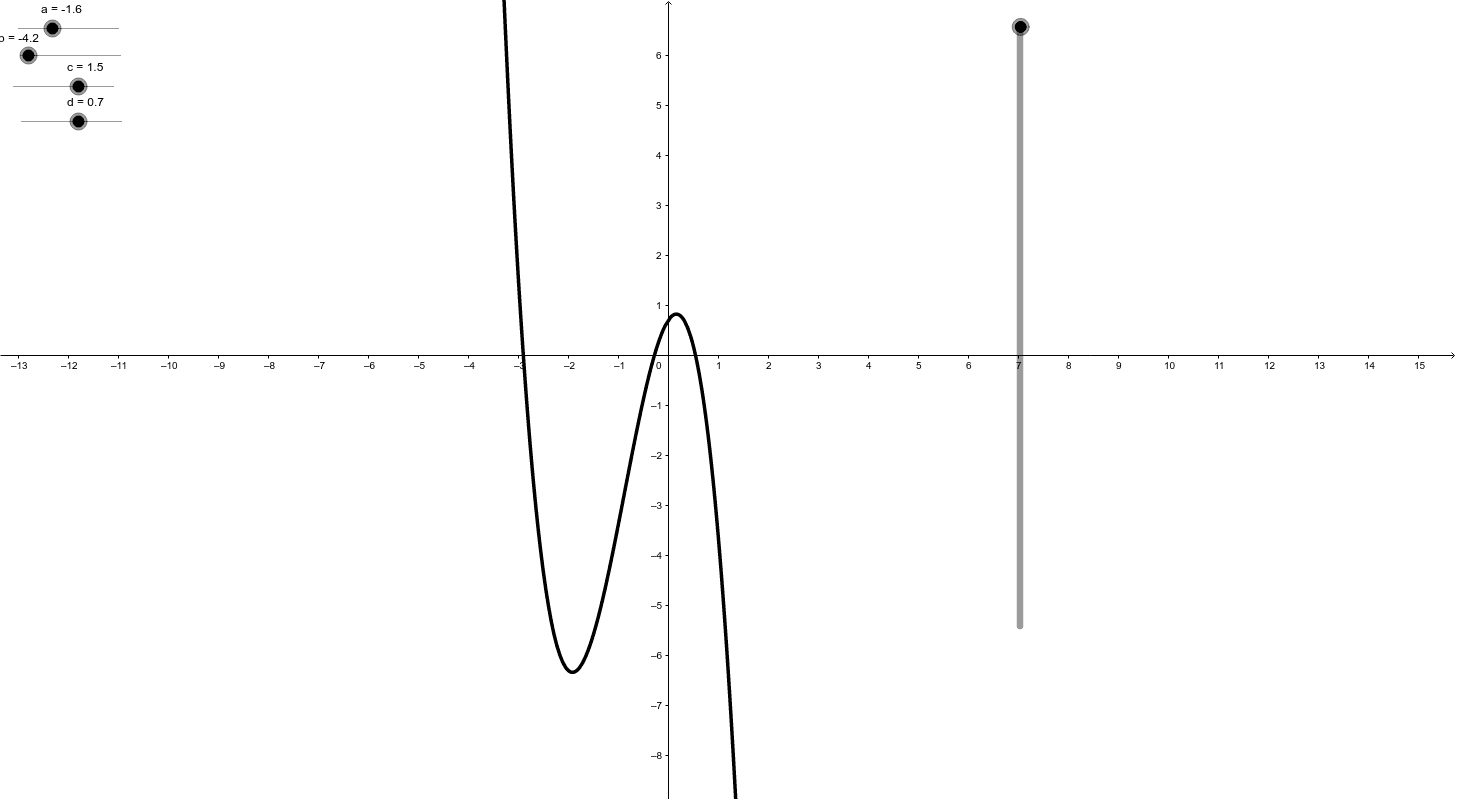
Características de la gráfica de una función
 |
Funciones cuadráticas
|
Mueve los deslizadores para representar las distintas funciones |
 |
Dominio y Recorrido de una función logarítmica
Dominio y Recorrido de una función logarítmica
Dominio y Recorrido de una función logarítmica
Dominio y Recorrido de una función logarítmica
Rubber Pencil Illusion
Have you ever tried the "Rubber Pencil illusion?" If not, do a quick web search -- you'll find plenty of content describing how to perform/observe the simple illusion. However, there aren't many attempts to dig deep into the math or physics of how it works. In my search, the journal article http://www.springerlink.com/content/wq4608017297535u/ comes the closest.
Sinusoidal motion is the basis for the simulation below (An imperfect assumption from a physics perspective, but a reasonable approximation I believe). Play with the sliders and checkboxes to get a sense of how each control affects the animation.
This models assumes the point H, where the pencil is lightly gripped, moves strictly vertically. Its y-value is a sinusoidal function of time.
Point P is the geometric center of the pencil. Its y-value is also a sinusoidal function of time.
- Why is a non-zero setting for the phase shift necessary to make this model look realistic? You may use terminology that you've learned in Physics class, but you may also just use your observations of the world around you if you don't have a formal Physics background.
- Geometrically, why can't the motion of both H and P be purely vertical?
- Describe how the slight horizontal motion component for P affects the position of the red sinusoid with respect to the blue sinusoid as they slide across the screen.
- Which conic section does the "trace" of the pencil appear to form? Do you think it forms this shape exactly, or is it just a visual approximation?
- So, why does the pencil appear rubbery to the human eye?
Saving…
All changes saved
Error
A timeout occurred. Trying to re-save …
Sorry, but the server is not responding. Please wait a few minutes and then try to save again.