Congruency and Similarity
Collection of applets on congruency and similarity of mainly triangles.
Table of Contents
- Congruency of Triangles
- Exploring Congruency
- Congruent Triangles: Side - Side - Side
- Congruent Triangles: Side - Angle - Side
- Congruent Triangles: Angle - Side - Angle
- Right-angle-Hypotenuse-Side
- Similarity of Triangles
Exploring Congruency
When triangles are congruent, six facts are always true.
When triangles are congruent, one triangle can be moved (through one, or more, rigid[br]motions) to coincide with the other triangle. All corresponding sides and[br]angles will be congruent.
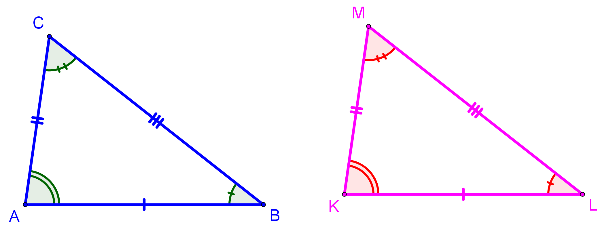
Consider the following two triangles:
These two triangles are congruent:
[math]\bigtriangleup ABC [/math] [math]\cong\bigtriangleup[/math] KLM[br][br][b]Corresponding sides are congruent:[/b][br]AB [math]\cong[/math] KL[br]BC [math]\cong[/math] LM[br]AC [math]\cong[/math] KM[br][br][b]Corresponding angles are congruent:[/b][br]Angle A [math]\cong[/math] Angle K[br]Angle B [math]\cong[/math] Angle L[br]Angle C [math]\cong[/math] Angle M[br][br]The good news is that when proving triangles congruent, it is not necessary to[br]prove all six facts to show congruency. There are certain ordered combinations[br]of these facts that are sufficient to prove triangles congruent. These[br]combinations guarantee that, given these facts, it will be possible to construct[br]triangles which will take on only one shape (be unique), thus insuring[br]congruency.