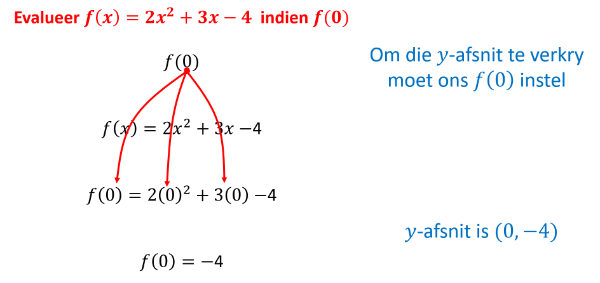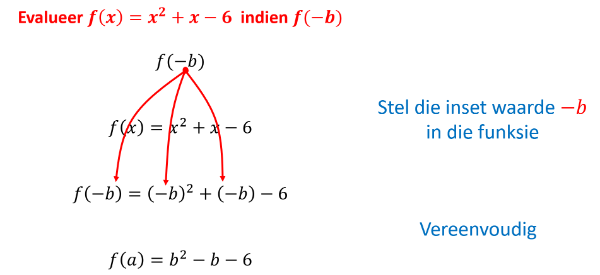
Evaluering van funksies
Wat beteken dit om funksies te evalueer?
Om 'n funksie te evalueer is om die inset waarde in die reel in te stel en dan die uitset waarde te verkry. Onthou jy nog die "masjien" wat ons gebruik het om dit te doen:[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAV4AAADpCAYAAABsk19jAAAgAElEQVR4Aex9B1SVSbrtrJfWeu+te2fezNye6enpnp7pmZ7Ott1tzpEgwZwAFcw5YM45KyqKmLMCiiRFcs5ZFDDnnHNE9lv7OxQeaVRAJEjB+tf5z1/pq11Vu3Z9Veec30D/aQQ0AhoBjUC5IvCbci1NF6YR0AhoBDQC0MSrO4FGQCOgEShnBDTxljPgujiNgEZAI6CJV/cBjYBGQCNQzgho4i1nwHVxGgGNgEZAE6/uAxoBjYBGoJwR0MRbzoDr4jQCGgGNgCZe3Qc0AhoBjUA5I6CJt5wB18VpBDQCGgFNvLoPaAQ0AhqBckbggyXeR48f4eLNi7h06xIu37qsL42B7gNVpA9wzN64c6OcqbB8i/sgiffOgzsIOBGAoKtBCL4erC+Nge4DVawP+J72Rc7FnPJlw3Is7YMk3sPnDyPodhAO4iDSjP75/nj+/wmcQA5yJDQVqchGNjKRaRTbOGXJ7tORjiM48qvyC+fC8hiv8POSvmc+tP9N6VRZrCvLLKu6vqnMwmEs+zAOIwtZUBjxtXC8d3mv2pLl8P51ebHt3xUD4ngIh95YDssvrk2vs7U8nqu2eVN9VJtlIKMAV6YjloXxJrZqfJXUfpaTgASEnwoH8sqRDcuxqA+SeDPPZyL0Tqh0jhQY/tlZEp4kYPSK0TDpboLOQztjS+IWIQGG7czYif3n9oP3Kg07lbo3fn3dc8ZhpzmKo5jvMR8+p3yEfI3Tqnt2zD05ezBpzSQps6g8+extz1le0JUgbE3aKmWr/I1fOZg8czwxae0kIYphC4bB/ZC73DNeUWUYp1f3xvGM74sKV8/4quJycDofcMZSn6WIuheF/jP6I+5JXEE7qXjGaY3TF35e1HuS+vTN0+G0z0natnAclsEJePzq8fDI8hDyVWW8rvzX5TFu1ThsjN0opKPiFJUH6z1l/RQ4Bzi/YpNxXON7lZfx6+vCX/e8pGnZ7/ce3QvPI55FjgGSZ+yjWEx0nYiIOxHS11g2+9aMLTOwPmp9QX/isx1pOzDWeewrfbsoW/msqOcJeQmIPhcNvChHNizHoj5I4j10/tArxMuGPfTiEDoM6IDWXVpj/ub5GLN4DD778jOsDFyJMzgDk64mWB26umD2poJkB1KKlHlwUPM5BxJn88IdRmb252kYsWgE/uf/+p/YdXBXgRJQ+agBwfQrA1aiYZuGMviN8+K9UhEsj+UmI1kISqksFX4Mx4S82/drj5M4WTBRMD4HE+Odxmmsi1yHhuYNxR7XUFcEXAqQcJW/qi/TKRt5T5JSZam4xjiocpRdfOWkwufEj2kUXsxrT/YeIX0SLoko4VlCgfpV8Wj369LzubKPeDMN36v4tG1z4mZ4HPYoKJ/PWLZKx8lqQ+wGBF4O/BUGzI950QZVD6bjc5bHe9UX6raqi6mbpuIUTglGChfW29hOlr05fjN2Z++WfArjyLgsS9XbuF7MS+HPV5at6sr3qkzaxXQqb5bJehqnVXXjc7YT3zOc79mPuo/oLhME75meYWoMMG747XA0MG0A/wv+Ek5bKDJMu5lijPMYWUuyfKb1P+8vZMw4Ki9VHp/RXtU3lM3GmGniLcdZoKyKKky87FjR96PxZY0vZbDdxm3cwi2s8F+B5T7L4Zbshj99+ic0sW6CuPtxokS7De8GUxtTjFg8Aum56Qi5HiJqeezKsTC1NcXMrTN/RZjsQIxv2t0UtZrXws70ndK5qBQYP+K2QSmoTkcCbN219Sv5sFOm5aVh2qZpsHKwgkVPC2yI2WBQSrkpQrKWDpawsrcSlZ7yJAW1W9bGp//8FKtDVhviIUUGccy9GDhMckCXYV0weM5gWPSykPBxK8dJHel2cfJzQpsebdBpUCd4HfcqSK9sXLB7ARyXOaLXxF7oNLAT3DPdMXLJSJjZmIna4+CMvhuNofOHok3PNug0uBN8T/nKwCbRdBnaRfKfsXUGsvKysDZirRBu9INojFgyAonPE8VWDlyuRPpM7QPaTSynbZwmRMDVCfMlUXIQ0zYO4o1xGzFq6agCgl3svRhLfJaI2l0buRYhN0IwZN4Q2I22w+R1kwtwJsFRFXse9RTC4QRATNv2bSsrB05grmGumLVtlthBGwfPG4z95/e/Uj5x2J21G04+TiCmxMjS3hLuh92lLNqpbJ29Yza2JGyRsOGLhguGrC/xZ11pJycLEmnc4zgMmDUAMQ9i4HvSVzA072GOObvmSL6Ms/fYXnQe3BlterWBk6+TkJ7XMS9pZ1tHW8zaMQvpz9MxcNZAafcJqyeAfTflRQpSnqdIP2X5g2YPQtqzNOw7uQ9/+/ff8EP9H3Dg7AGEXw1H78m9Yd7THL3G9ULUrShRvK06tZJJm+3AvkoCb9e3HaZvmQ667+wn2mND3AZ4H/fG1A1TpW7hN8NhP8EeZnZm0p5My/ZbFbQK1r2t0bZPW8FbtS0x08RbVmxYjvkUJl52EDY0O9lXNb+C/Xh7LPVbKoOCajDqdhTqmdQDyYEETSLjcvhA9gEh0LlucxF1Pwq/+6/fgYPGI8YDPzX5CSQlEo8aYCwn8GKgDA4qa7oyGB55LxI9xvRA4BWDwmJ8DraiiJcdmXY0bdcUB7IOYOGehajRoIYMIpIH8w06EiRxajaqifQX6RgwcwBadmyJuJtxBUtADs6OAzuCE4hXghdadWmFptZNhWhqtaglpLkufJ3U1TPdE8t8l6GxZWMZcCQm2siBRNLigNwTtwc9x/bEx59/jDVha2R5WbtFbRzOPYwe43rAxtEG4cfD0W9aPyHlzOeZaGDWQIjQK8sLZrZmCLkcAi7PB84cKBPZt7W/RWpeKgbPHSwTSWB2IIYtHIaOgzpK2bS3sVVjsZ/1sOxlKbgRZyrEfWf34cdGPyLsZpgQQIsOLbAxYSNsR9vKZEFl9oc//0HcPn7H/UQRMi1VXOturbEpfhO2JmzFD/V+wIbwDXDydsL3db9H0NkgmShZJienhKcJ+KX5L6+4Z4hP0oskwZPxOKm7x7nD0ckRdVrVQcozgwJlPCpITpQkojXha/C7P/5OJh+XIBd89dNXCLsaJm6XPlP64AIuSL9o0bGFTNScwKdunIpdsbvAdpvnPg/xd+NRp2Ud6Rte6V4iGDZGbYTbQTf8/qPfS98NOxeGPpP7yCrPK94L5rbm+Of3/xRid5jogM5DOiMoO0jaq8fYHsh8mintxr6U8TRDJsuRS0ci7FiYCIBe43sJ0bbq/Gvibd+/PWZtn4WhC4fKZJD1JAvL/JaBJH0o95AIEU5SgVmBkhdFhf85f/zY8EfsydqDVYGrhLzjHhr6LzHTxFuOhFlWRRUmXi5hOJtySbg+ej16jumJeq3r4ZtfvsGW+C3y3NzGXMJIGPTNcqm0M3YnGlk2kkHMZRZJgMs5Dg4SIjuzMfGyw6glY7N2zUQ9kfA52EmoaqnKeK8jXqpz+mzpb957aK+UQzLg6YywK2GiujwPeoIK6ssfv0RKXgqmb5ouqohKjXUlcYbeCMXPTX9G5N1IsZdLXSpx2ktC25a6TVQu3S+bIzaDA/dfP/wLs3fOFlsVYXBQDpw9UFYI66LWgeTGyYqqjHUMuxOGwAuBOHDhADxSPDB84XA0bdsUmbmZotZJuEv2LhESoX1UhoxD++q2riv+whr1a8jzjWEbscR7CT75xydS3zZ2bbDUdymu4Rp2pO9AI4tG0o7Ek/YRU9pPlRtwOUDs4TMSLxUelXfz9s1l0mU7MI0iXqos+vVtRtlgvMt4nM//7zmuJ0YtGyXkRbIhaZJ42fZU8CRt5sN/tieJ2WakDYYvHo4ruCLLcZIi/aBqAuNynOqUCtol2EVWOcSQExvx3JK0Bb5nfAU32k/MOalTDZvbmQveZ3FWyJrvF3ktwvf1vpel/JaILUJa7Qe0x66MXZIH8417FCftz5XaOZwD1XATqyYIuxWGb2p9I5MA8Z6zcw7++sVfEf8kXlQpV2a01++0n7Spe6I7ug7rKsqUfa1159a/UrzdR3bHx3/7WGwizix/2f5l6DigI3bn7JZ+tdx/OTaFb5KVEftl8JVg/NzsZ8GOEznLZ99X2GriLSs2LMd8ChMvBwA7Njdc6M8lAbPjc8OD6oSDi34qEkv6o3TxdZFUh8waIj5YDmJ2YC5FSayMzwFEvzCVpSICNRg5II2JVz1XnYqvinhNupkIMbDTMR077vrI9WjWvpks7anSqSypuNeFrZN8uwzuIiqXSpiDgRt0dBXQLubNSYZqr07rOrJ5xcHMTRMuCVkuiZFqnO9bdmqJ/hP7y7KSy3z6pRW5MD+SD5fzJCYuDeliIHmTOKnK6EYhoVCh242yE9IjLswj6UkSJrtORssOLWWwex7yFBeKIt56pvVkkiHx0r/Ye0Jv9J3SF3SLxN6LFYVLPzjbim4FYsq6KbxpB9uUS2G2JZXzZVwGiYBt5nPSR9wfCltiY0y8JHOuCjiJkUDZL7jk5/J8sddiwYQkQoyJGd0KChvVlsTIboydbNYxPSeg+qb1ZcIriniJIXFnm7AvkXjpb2b5dCutDF4pGNPNMGXDFFH/nLAYf1PcJrC/cFlP0TBo6iAhS2LmvM/ZEN7VRNqHqysSHPsNcTpw8YAIhf0X9uPbWt/KSsZhgoPgzc1WKnTbUbbSPsdeHJOVHdVt34l9xX1Cl1FRxEuS5v4C+xH77CLPRTLRL9+/HJ0HdcbW5K34/KvP0X9af/Sa0At9p/aVSZbYhFwLweBZg8F+0MC8AUKuhBRMVpp4y5Ewy6qowsQry9JT+/CXv/8Fy/YtQ0ZeBg4+PygDjAqCHZvKaHvqdjgHOsuykR2Kz9kpRjmNQszDGHzx3ReyE04i4IAdNHeQqAM1CPlK8uQ/1QXJjUSanJcsm0h8VXFJgPTJtujUQgYgOzUvPueScvTy0aIyqWL+8e0/ZABxWc0dZPqnuZtOvy6JZILrBBnMHPjKhtRnqahrUlcIhAqdvmdu5LFeVI7bUrZJvUhSVGq0k0qLvkPixXxIKnzGzUISLzci6eooIN5OLUSZf/avz0RB38ANOTlBJUtCpprk63Vcl4E5euVo8VPSXUP/6y/NfhE1yWU/l9Cs14FLB0DVSb86SZ5+eOJNciKmxsRLQo19GCsTIEmGipTKkAqNLg2fEz6i8lWbsE7GxEsfPMmNdSLu9Jdzac9NViptkgn7AE+f0N1CH3hRxEs3C3fwFfFyMudKw5h4qf5mbpkpGNLtoIi3WdtmMuFTldKlRUKlP5R5sT9ycg29Fip2yOQ0pbf42amq03LTcBVX5aQB1TGVMydDtmXGiwwhwgV7Fkjb0V1BlZzyNEUmSZ4u4V4H29t+kr3Un+4HTkI8//7J3z8RFw4nMrqbuPogfpxEuTGr2oH14F4EJyrPbE9xnSTcTRBhwnpG3IiQ/ky3kOyrHFghkxSVsKonxQtVuGu4a8EegybesmLDcsynMPGyw3BgLd+3XPxKtZrVEjXAGTrgfIB0aqol+iSpgjjTW/SwEPXGwU7SonKgT1I2vHpYwNrBGrF3YwsGF8vgvxrkzIPkxo5JNwUHsfHmDO1hODf1qGh50edFpeC01wk1G9dEl4FdhLxIUOy4s7fNFru7DuqKbiO6CXEFXw2GR6YH/l3z31jsubig47Izb0vcJuqrnUM7eeXymvZwcNLlkvY4TepDFcWNRRIeyYd1YF1IvNxg4eYaicElxEVUGYmXflWm44REv2B9s/roOqQrOvTvIARJBTVy8ciC8qnm4q7HySYXFS/Tc1JLzk2G91FvNLRoCKseVrICmbZhmixX6dMl2ZOENiVsknZRA17hTRs5gElEJBwqRypQHp2jq4GDX7UJ0yjite5jXeBa4sYdNzmbd2iOftP7ST6RNyNlMubKhxMIFVlRxMuJjEqOkx9JOuBigPjK6ddXxEvM6Qfmsp6TLd0jfMYJjqsDTiqsB90AdLNws4/hrM8453Fo0KaB4M5N0PDr4RJGX3J98/qwsLMQgg09HyoTPScrYsT+RVw5ybbv017qxkmFE4dbupvUx7qHteA9b9c8mdzop+W+gbhgRtpIGpI9xQnble4l4qE2OYkl7aQIod/2Ei4J9n2n95XJpG3vttIeS/cuFbeSdU9r2UuhXz3tSZooZY4TuqPY9xIfJxb0PU285UiYZVVUUcTLQUfC4A41d515ZpEd1FjB8Gxr/NN4Uag8h8jlNAdtxLUIeJ/0lk5Hwth9eLcMKqY3PgKjyICvVA30WzF9Ym6iDFrmzc6qCIBHqeh7Y0fnEp+kT5eGWhrymZR/J0KIn4OJBOx2yE38YfQjkvg4gOkTZpjyk9Euki83C90y3cTlwAmA5dM2KlGmYx2Ih/cJb4nP8lQ9eE8yUOc2mSb4WrDkwY0l5sO4xJAnBHgxP04GxJn20i7Wi2qfA3PimonoO60vsl9kywBmPrST8benbZf8mY52siyWSTt4/IzlKfyMbeQJCdZNuRRCb4bKhibz5HJWxeUr05MgOYFyIiFx0n6qZbomaAvLYz1oG9sg5lGM4G/cfipPwehmmChc3rOtucxPfvFydcPn7EtsC9aHbUw7+M86kdB4z3gMY7nKVmLB/Qa2IYmcbca46jnt43vWQdrnarDkw/IXuC+QySf6QrRs6nHyZx5MSzypqNmf+Z7lET+OC7a36hfsU0yj2pRtwjqyTGUjbea5bMYj5n5n/KRfqnoyf5bD9mW5nFBYFsvgaoIX66X6LvPVxFtWbFiO+byOeFXnYiflPzs6n/Gf9+oZ72W5lv8JHRIhOyRVD+OqwanSFvXKTsV8SIDspGrAGMflc5Zj/K86H+PTHsZReTHtm54zXuGJgIOB+TBf3jMPlZ+yjeFF2cdwpmFa3rM+TMs8lF3q3jgPxmG4KothxGx7wnY5rjTPbZ4QHstkHP6zDOKg8ldpFYbGZas0fKVdTKvSGdtsbCPj8j3j8nTBd3W+kw0kVW9j+1X+jMvnfCUOqk4qXJVvjBHjGNdLxVVxCteDdvOZiqfsUe/5yji0wzhe4eeF24d495/eX1YyE5dOlL671HvpKyRLvGmXKou2q/qqe2UfX/lMvao0yg5iZNwWhevJclge46m0qgyWyXv1nK+aeMuRMMuqqKI+uWbcqCW9ZyeiWuHxIyq3wp2kpPlVx/gcsHSt8AQC8asIDFW5PDnBTR/a9KG2BevK+vH42sS1EwvOCFeV+mriLSs2LMd8XvddDSTQ0v5zxqY/izN2afOozulIBFRh9MESy4rEgu4FrmIq0obyKJt9lX2WJzO43C+PMsuiDNqdiEREnI7Q39VQjrz5zkXdvn8b/sf9EXgtEEHXg/SlMdB9oAr1geAbwfA57YPsi9nvzAWVNYMP8rsaCPaDRw9w4vIJfWkMdB+oYn3g+KXjuHzzcmXlzDKx64Ml3jJBR2eiEdAIaATeAwKaeN8DqDpLjYBGQCPwJgQ08b4JHR2mEdAIaATeAwKaeN8DqG/K8vZp4FwccCFJXxqDsusD7FO3Tr6p5+mwyoSAJt5ybg2ekIlZCCSs0JfGoOz6APvUicBy7sy6uFIjoIm31NCVLuHZGMNgS1kD6EtjUFZ9gJPYqbDS9UmdqvwR0MRbzpiTeOOXA5kbgeM7gOPbDVfWZiB1DZDsCvD+4AbDfVkNzLflk83y1wKHNwEH15eubNqfvQVIW1s8Qk1bZ6izsi15DZC1Cchg+UVMTMyX+av47/LKslnnN+XBcLYPMWE8tk36euDoNsOVvq5oO9+Up+SzBmBa4/JZX+Zt/Oxt+RiHa+It54H8jsVp4n1HAEuanMSbthpwm5qJQW3nYIDVLAy0ng3XUWFCuIc2AcuG7MPu6dnI3PBmYjAeeKW9J9kmu+Zhfj8PxDg/xIph/vCceVSIvyR5Mp/E1c/F9qgVD95KvoyftDoXSa4vCsiPhLvGMQIHFl4U8jUun0QZseyO2Ed7md44vCT3JL0wp1twHhYgeXDCME7P95wYVw4PxEDrOdg2MQWHNhomw2jnBxjTZQUm2KxG/Kqnv7LTOJ/X3bP80CU3Ximfdd8/7xwWDdgrpFzS+mniLelIrNj4mnjLGX8Sb84GYEi7eWj4fRssHuiGaT1Xo963pnDs7IQTOwHnof7YMyNHiJfq99g24MjWV5WkUl9USDlbDAqMRM14jC9qzNWg1qjQ+IzkwXRU00q1MU2Sax4WDvAU4iXZ7J11TMqmumQ65k8SUYqT749tf5kfw1geibvR9xYIW3YbZ3YZlDuVnFLCzEsUsSjFFzLxkLyYlnlkbwI6NBmINaMjcGIHxIYkV8Mr7fWafRzNa7ZDoksucrYaymda3h/dalDKqm60j9ixfJI247B8xuNzj+lZaPFTRyn3yJZX68L6zbDfjOY/dcDSwdvRvGZ7bBwbKzh0bDIIwzssQl+LabBrPUYwVcStsGU5bAfmo+ommOXXnwp615QMtPipg0wgDONF4l0yyEfsZbuoNlKrH5KzaktODMarAk285TyQ37E4TbzvCGBJk5N4s9cDw9ovFOV0yRM4vQsId7qFGv9sgJAlN7BpXBy8Z5+QQUYl3KP1OMyw3yqDmCRCkuJg3D//HJYP3Y8JNmswrMNCHFhwHmO6rsTwDgsRu/KRLJGp1vq2mYY+baZg78xjMsD9F5zHAKuZorSZB10LVH9Ms250FPzmnhGiovK2az0OC/rvERdA2NKbcBrih1kO2+FgNhGeM4+IMlTEG7fqMcxq22Cy3Xo4mE3CujFRYgMJf8kgb8mLr1y+rxoRjL/96UtMtlsrBEuFRzeDbevR2DE5DVsnJGDXlINCYDsmp2Pd6EgELroMi3o9pA6rR4XCaYg/AhddwezeOwRPr1nHJM6w9gvQo/VYSUOSS3B5jJkO2wTHyXbrkL7uGbxmHYdlfXvB2Hl4AJYO9hU7WBcS3FpHlncJDw4A/S2nS52YxryunUwKnEBManWV1YFambCeQYuuyCpmQndXzOvrjgMLLshks2iAp9TfabCfTAAkfsv6vWQCWzksACuHB4P4uowIFncD8+FKiO0UsPCS4BCy5Lq0bT/L6fCcceSVVYkm3pKOxIqNr4m3nPFXxEvVRIKggiHpUPG0qWuHrROSYdvSESuGHcDGsZFoXasr3KdFo6/FVIzu7FTgA+TA3zAmBl988h1WDt+H7i1GoMYX9bHG8QCsG/TGuG6rEO50HWZ1bLFlQjRm2m9F85/aI8n1Pkxrd5cl7fx+7rBt5YjUtbmivoIXX0XnpoPF7bF8qB+s6ttjz/RYUXZz++xE0OKr+PvH32B2752Y0mM9mtSwRuLqx6LQqOzoOvjpX43R33IGnId7o/ZXLRC69Crm9XNDu4Z9JS+bliOxoL87/BecQ/3vzLBxXJwQHVWjIt49M7IxpN18TO+1BRd3A5N7rEdv80mIWHYbnZsNxrrR4WhdqxsCF52U9P/85HssH+oL//nn0aXZEFHv60eHo+43raX8qT03yEThMydV8Jjea7MQdtfmw7DWMRQmtbvDb+6xAiKjcmV7JK/JhU3LUfj+H/UQ73Jf2sSmpaOQIFUzbaFrhPesf4LLA8PEY7sWc/vswh/+80+irOf02SlKfvf0WLBMp8G+8Jt3Bl2aD8UaxxAh85AlZ7FlQiLa1O2BRJe78mxBfw+wHdo16ou4VdfRvnE/TO2xHs7DDqB9o36Id3lUoKg18ZbzQH7H4jTxviOAJU3+OuKly8CiXi9sHp8oy9i1jhHo0mwYOjUZhFUjvDG6y3Ih1sTVz2SwcbCvcQwXQrvqBSHLzk0H4YYP4DIyBL3bTEb2ljzxFa8Yuk/Ude2vWyJ+1SPYtholBDTLYSu85xwTF4JFvZ6gouplOk6UonkdO/QyHY9VI7wwyHq2kKzPnJMwq2tbsMwnge+ff0EIi8QTu/IxWv7cSZTbxT1A56ZDsH5MtEweVNzMq5/FNDSuYS2qvVPTQYh1fkkeinh3T8+S+s7r447zHsCs3tsxuO0cUFH/8EV9/P4/PpJVwZW9rGswurccKa4NKk+/uadFTc/pvR0/f9lUiC/e5R42jI3FsiGeQrIjOiwG/dDf/r02/vCffxaFfXLHqxuKxJe+5B2T44V8qcxXDQ+CXevRoGuC4SR5thPvDe0RiXaN+skK5tQu1n8wNo2LF1dFf6sZUn+uFIgblfrXn/2M//rtX7Br6kFc2A2JS8XvOioCP3xRD0sHeWHZEC/U+KIBXEaGYkTHBTJBTuu5AR7TDsmER4XOSxNvSUdixcbXxFvO+CvipWvAsZMTzrkb/KWJLs+EKMKW3oC92UQhVRIvFdLcPpswredGcTckrn4hRGkY6OEyuOmqoMuhh8kYyY8uAua/d9ZhmNTqhkm2KzC/vwca17BC9Ip7SHB5iNWjgoRkqVpDFl9B24Z9CoiXZGJa2wb2phMwp/cmTOmxAUsG7cWemUdg3bC3uCYSXJ4JefsvMCbeRzCtRVK5LEq+S7Oh2DA2Bq1+6Yw+FlMwW/Jaj8UD9wrxkaReR7wjOi7Gwv57cNMXmOWwTZbc3NiiX3xkp6WwauAgy3ROPiQzui+CF18SpTii40I4D/MVkqLN9J3TluVDdonCH9lpCcKdbqPRDxYY2XGpKEm6CdRpDL7S3RG36gk4qdHfzpXHlgnJ6NB4AE7uNChiEig3SZmWE6fLiFAJP7UT4MXVBH3DzWq2E/tn994oKwVOhHQlNfjOHMM7LEaHJgPEfbFlQpIQO90ONf/VCPP6bsWMXpsxrvsqeM0+gZQ1T7B+TAT6WUxGvW9N4DP7uODM8nlSRh8nK+fB/A7FaeJ9B/BKk5TEy821wW3ngirTfVoi1o0JFoKkSqXC4+Cm39Gw3HdAyJLjmGS3TlQfBxldE3Q1rBoRBIu6PXHGjT5UL3RqOgAXPIBFA/dicNt5WDzQC42+b4OIZadB3+Y/Pv5GfJAkoTWOYfCYlomG35lj/7wzspzlTiYTD70AACAASURBVDtV6ppR4ZjTZzu6Nh+KsKUnheio+KgmqWjpAyXxNvmxLfbRR7whf3NtpWFzjWTMzS36MKn4pvXaCJtWoxDudBJD2y/AJLu1SF+fi0Y/WIpPmflJnTYBHZsOFAU4w34LTOvYwGtWAhrXsERv8ymipE1qdxUfKSeKsd1chNi7NR8hKnPn5HR887df4D07B2sdw/HpR//ClolJaPlLZ0ztsQGBi46g/remouTpN6Ubhkf66OJx7LxcMKXLg24G+lY7NhkIr9lJMinxJMOhjZxsbOQECCcjunTS1j4TwjYo/rvSjgsH7BF3wGcf/UtIe4KNK3qajEOY00lpd/qkuVHIvFi+eV1bTO2xCTunZIjfOWr5dSF6ulTcp2aAG3qBC8+K35qnHvzmHkWD783hOTMLu6akyKmLNBdNvKUZjxWVRhNvOSNP4s1whRCOdQMHGVQkQvodOXipnLgpw11v7sDztEHX5sMxwHoWghdfFrXJpSWX1dzcmu2wXXyOVF48EkafMe+pejPW58qSvXvLUeLTJfnwSBbDuSPPi8qOO/DcaDqw4CIWD9wjy3MSOzekqLqpnmNX3pEjUFTe3OCjP3eK3XrZFKTdVIkJLk8xyXatlMFNLRIMT0jwflqvTejcbBhGdlyCaOe7sjRnOI/Upa7Nk/QkcNaBBE91Rx+4g9lkzOvrJptd0SseCIEyHm2l8mVduGHHCYmbhFTJxJPEPa3XZiE+5kdf7eC288FNLm6k8TgZbeLxPfpbh7afj6TVBhJl/ZJdn8mRMdafebGOdIXsm3cOPUzGwt5sAugTVxtrJOy0tc+FPEna9MXyVMS2SalSVxI17XLsvEx8wUxLLImN79xT0k5Uwdy4JPFzI4+uHtq9fnS0POMxP/Vs7ehIUfnz+nrIBHvQFTitP0BRzqO59MVp4i09dqVKSeJVH6AgSXKQkfh4kby4scPBSBVIgmU4L8blM4bzOV/5ni4Hdc90PH7F50oZk7yZnkTKi8qSYapMvnKDiBtd4U435DnTi/LLT8s8FLmyPJbPi5OEWp7zPdPwGcugTYzLDwXwPctRdWVeDBebjPLj8SjWQcpaZ6izqj+PTzEfqS9PdeTXnbYyDfOjDSo+8+Y982JahQOfKWwUdiRy2q3qpY6gKZt5FE21DYmWz5kf06lyaUe40020b9xfVhPcQKOSjlp+U+KpvPhKYmd+xuULViT3/PY0biP1jPVQ+ahnjMdLuxpKNRwrLJEm3nKGnsTLjRA1yCvylUTGa3SXFeAxJw7sirSnqpdNUuZKhRuJVPJ0uZQXpnpzrZwH8jsWp4n3HQEsafLKRLyK6KgCqRDVe/1aOiyolKk+5YMa2wzuID4rDzw18ZZ0JFZsfE285Yx/ZSTe8iAGXcb7JWBNvOU8kN+xOE287whgSZPzayFjFwGJzvrSGJRdH2CfOhFU0t6o41cUApp4yxn5q4eBIz7AMX99aQzKrg/k+ABXMsq5M+viSo2AJt5SQ6cTagQ0AhqB0iGgibd0uOlUGgGNgEag1Aho4i01dDqhRkAjoBEoHQKaeEuHm06lEdAIaARKjYAm3lJDpxNqBDQCGoHSIVCtiDcvNw/Pnj7Tl8ZA94FK2gdKR2NVL1W1Id7zN84j6HgQAk4G6EtjoPtAZewDJwIQezIWj58+rnpMWkKLqwXxPn/2XAZa3Is4pCAFyUb/fJ+OdGQgo8gw47ilvU9FquTP17flQVsK2/i2NEWFFycPVRbtSkPaW20rqpyyeEY7mA9tKA5GbyqTebxrXSoajzfVzzjsbW1cFngal1cW92/ClmEBtwKQce7DP5BcLYj30eNHCL0YKgOSnVV1WJJtDnIQeiMUBy4eQCYycRiHhQQYxn92NpWmpK9MK/nlJcPnlA+ScpOQhaw35hl9PxqJzxOFgEpanorPAce6JOe92XaWRZviHsch/Hb4O5Wpyi7JKwda0oskhN0KE4wj70Yi+kF0qe1gflH3o+TifUlsUXGZLu5JxeChbHjbK/vVQRx8Y/9kPWIexiD+aXyp8XybHSUNp02053VtzPCox1FIOJVQQv1Y9aJXC+J9/PgxQi+EvtIBqbISHiag67CuqNm4Jmo2qIlGFo3gkemB4ziOPdl7MG7VOGQjWwYwyewQDgmhsYOw85OYmQ9JjgOhcEck6e5K24Um1k1g2tkUDS0aYlviNiFj5sF/lYb3zM+qlxU2xW+SOCpMvTKcNiilyudMx7L5XCmcpOdJGLpgKEhkTKPSq/iMy3+LXhZwz3THush16D2lt0wKyg6Vn3FalV7VW8VhGt4bl8VnxEXFUfnQdhWX9yT8nmN7io2Oyx0xe8dswVylZx68J96sH8vgP/Pgc5UvXzmJTlo7CVM3TJV7PjPGRuVh3Fa8N8aTE+P66PXoO7VvQbuqtme5zIPxea/K5j2fqTBVPxXOV4bzuXFZTMd/1pFxWB8Vh89ZLvNUWCi7GWd39m4QL/YxplU2qjjEwtbRFvPd5xdgwXgMZ1zeq/cKR5bJvFU4nxssNNio8mY62qzsY5zC9TeuJ9MxzkmcxAKPBeg4sKP0NT5TdWeeLC/yUSQSTydWPSYtocXVlniP4RgGzxkMk24mSLqThJT7KRi5ZCR+bvozcp7nwHGZI+q2rouISxFCBFSPOw/uxL6z+6Szs9NF3I5A8otk7D22F8FXgwtIWnWijBcZaGDeADO3zsRpnMaCPQtQ37Q+UnMNpMSOx4FVEB8ZaGrdVIiQBMDn6p8TQNCVIOxI3yGKjAOEHZXx9p3Zh10Hd0lcDrgdaTvwZY0vhcA5ABiP5bA8DgLPHE/E3ItB6y6thWTi78bD77SfDCSmJxmyriyb5RjbmPAsQRRlzKMYuB9ylwHHPD2yPERh8Z5lMp3XcS94HPaQ93zGQUbFwzqE3woX26nuuRpgWQcuHEDQ1SCxkfXyPuEtF++Znkop/km8rFBIPKoshRHjBF4KRODlQKkr68KVjPthd3lPm6jug68FCybEJeR6CGIexMh75iPtejdCME3JS0HknUhZgTAPlk9bmIaTGuPyP+pelDxjeQnPE7AzYyci70Ua+g2SJQ1x25GxQzBiHkl5SYi6G4Wwm2HYe3yv2Mf2cc9yl7Sxj2LBi3Wk3Xty9sD/vL+QaHZeNoYvHC6CIeximDzjyoXlMg7J+CiOol2fdpixZQaO4EhBPyIeibmGFRVtZ79lOYwTcSdC2p19nXmwrbiCYJt4HvWUOjKNwo1tR8zZX5iWeVBls+8wLfNgPTlOuKoJPh2M6Zumw7S7qYib5NxkaV+1MmO+mnhLyOCVOXpRipfE23daX7To1AIJtxLA95yR9x7ZK4OTnePTf34KF38X7MvZh2btmqG9fXvUal4LwxcNFyLtM6UPGls2Rlv7tvil2S9YvHdxAfmyEyW+SBRC4oBm/l7HvITYD+cexljnsZjoOrFAjTA+B17Lji2FDDk4mY7PD+UdwtgVY8UGS1tLKWv3od3IepEFh0kOMnmQRBtZNkL09WhRfP/1l/9C70m9JT0HCwdI8pNkdBzUUQi3+6ju+KbWN/A84oll+5fBurc1zuAMnPc7o55JPVh2t0Trrq0ReDGwQJWQODnx1GpRC12GdkHLTi3RpkcbDJ0/FBa2FqjTqg6CLgYh5UkKOg/uLGHN2jeDua25lO170leedXDogF+a/oIle5cIkTKcdXWY7IDxLuNxAifE9uYdm0v7DJw1UJ6tDFwpttH2xlaN0XlIZ6Q+M/inmZ5kM2TeEIxYPAJncRajl42WVYZZNzNY9LRA8v1kbE/dLvUnoZEo+Hy+x/wCcuIE5xzgjE6DOsmk2qJjC7Tv1x5WdlaC+/4T+7HUbyna9W0nbc08aMdSn6XwO+qHhm0awsrWSux0CXTBKZyCe4a7rKYsbSylv+xM3SmYsq3ZrxzGOgg5te/fHiZdTGDdxxo1G9WUiS3jSYYoRAqExtaNMWXdFCFits1fPv8LVviugNdhL8mnXa92YiNFAyf6TgM7Yda2WVI39iP2qXb92mHOzjmCJ11sXI1F342Ga6Ar6pnWg0V3C8En9FKoTHC1W9SGuZ05bEbZoHn75kKsnIA++ccncAkx1I9YbEnaArdkN9Q3ry/1Z728j3pLPbmSZDkDpg7AhNUT0HFARxkPpjamInbYv2kf/zXxVmYmLaFtRREviSj+YTw69u+I7+p8J51u0OxBSHiSIJ3WyddJBtdFXMQ4l3HSWe/iLnxP++Krn78SJcIOZNnLUuJTcX5X9ztE3np1eU+1wg6fmZcp6pekLa6MnD3Ye9SgdBTBFkW8tJPqquvwrqDKvIM76DGmB/rP6I+wa2GwHW0r5H0FV0CSmLVzlpAYCcDY1UCCmLpxqpAlJwEqw8+//lyU1GLvxUKICfcT8EP9H0TB38ItmRja9mkrBMNBoYiXA55KliT1+Vefy/L+Mi4LeU/fPB2e2Z7oM7WPkB8nMw5eqnDHFY4wszHDeZyHzwkfkJhoIwcpMbBxtMHkdZPhHOgsxEoCZnoSlGuYqwz0L3/8EokPE5GalyqTGHFXy201mY5cOlJUPds14kaEkF+nwZ0wYNYAUb9N2zaV9iMmJl1NpG15TxuoWp38nGDZ01LU7L9q/AuL9i4C6+cw0QE9x/eUSYSTTOjNULG/UZtGovo4yXB1w/rRXUHyjLkRA5bHSfk2bmND7AYhocRHiYL1Mr9luIRLMpmTwEjUPid98Ncv/ipqcOyqsUKW7IfpeelC6F5HvcBJiBMWyxq7ciwWey3GPdzD7qzdooTZVl2GdCkgXtaNdZy/e770Waab6z5XJsjEJ4n4sdGP0hfY7mwDTtBUqV98+4X0B7YFyX9zwma4HXTDHz/+o5Qb+zAWrTq3EjVc16Qu1kWtk3ou8VkCk+4mSM9Nx3e1vxP7WE+Sfhu7NrAba4cBMwfI2KAwUGNAE28Jya0yRy+KeLl8ZuckCZKElnkvkyUQFW3G4wws9V0KKwcrUVGpL1KxyHOR+EE5OKgU2VlIgJz1OeBJsFScmxM3FxAByyDpktCatGsi/mS+VyTG8o2X8UURLzsk4/lf8BcF5zDBQQYW3SRUdRxoQ+YPgf1Ye3z101diJ5e1dGlwScw8mQfVIMl7yoYpUmd5P6wrdqbvBAdJh/4dsDtntyiZ7iO6o9uwbkKStVvWFns5AdAOug+oiNVylIp/a9JWXMAFGUj0i1NtbUncAk5kPUb3wD+//6e8j7waKcqvRuMaomgjb0YKcXHCoI3Ek8Q9eO5gIS27EXawG2kn9yQXYk2fPNuMeNNHvTVxawHebAdOSFTNc93mio+TxE0ypd+c6nxbyjaZfJTiJXkxrjHxLtu3DNYO1rLx18CsgbgruBqg/7jb8G5ClN1GdJM+wri0mxtydFPRxUDb+N/EqonEIfFQNdP2DgM64Oufv4bfWT8hTrqJSGoWPSyw3H+5tBPtZTwSHFciDc0bwma4jWDxVc2vQFGwKmiVEKHYnZsiqr335N6wsreSFQnbqjDxsi/QLUJ3Fl0oVOqrw1aLACDRdx/+st3pIvM+7i3ql24D4sgVBNt31vZZstJieU77nNBnch9x33z2r8+EyNl32vZui58a/4Sw22EysdIdRww5rv7vf/5f/PYPv5XVB9vMeAxo4q3MTFpC2woTL4mPnZCDgUtPqhkqCpJHjQY14JbthhX+K8ClH5UBOyQ79IaADdgQs0GWycyDyy8OAsbhQK7Tsg48sj1k0CnCjL4ZLept1JJREo+Ex46mBqdxp1PEuz1tu3RSDkCSjN8JP/zc5GdMcp0Er3QvsMNzOe2W5iakNH/7fPgc9oGlvSXmuc1D3NM4kDCMFS87eI+xPWRpx3pysFv1thK/IImXWNDX+G2db7EjZQfcUtxEtZFYWFf+K+LloKSfkO95vzF2I87hnGxIcVCuClglbgcndyd4Z3ujeYfmWBu+FlFXohD3MA7emd6wG2OH2q1qy4Clm8SYeIcvHi4qzzvdW+pIjH2yfWTQdh/ZXUiSWHEJvC3ZsFnJ9Ip4SQ5LfJeIsuNg5wQlKraXpbQ3l8yMyzAq3jcSb5sG4jelEiWh24y0kXZcHboaJF8SMcmLG5pUuPSZkqQ4UXHSWhu1Vpb/7E8eKR4ySVH9ht8Jl4mevnW2Bd0L3FhkXyKZmnYzFXVO5UmXmFeaF3Zl7MLCPQsRcj5EJlhOJKwD3SJ0IWwK3CQrA7phiE9h4iVG7H90kQ2eN1iERfKzZLgdcpPVGrF0T3GXdl91YJUob7ZN7ONYmbw4aXEccJVFXzTrbmZrJq4ZquOvf/la9ieYx6a4TVjqvVT8x3Qz7DmyRybkOTvmyMRHxU5ipvKnrbSNfUwTbwnJrTJHL0y8bGSSmuNSR/z9m79j9qbZWOO/Bj3H9RTCOvj4oCzlqGDirsfJUnnYgmGIOhUlS+iP/voRqIKpDDnY9ibtRf+Z/UWBHMw17BpTEWfmZoLLL/pEt8dux8qAlbIUYxg3mLhMJmGrTsf7+ib1RfGtDVor5M9062PW42///hu8jnjJ4P3iuy9E2ZFcvvnlG4SeDsX68PX4w5/+gCnrpxiWd3W+w9qItcjIy5AOTaVNdfh9ve+xOWKzKCQqD/p4uenXokML5OTmiB+Pm4whR0OEjLm7r052kGi5ycJlKTdW+J4nQngqgmRO5cfNnDErxwghR52JksH329//VgbitE3TwOV46LFQUbYckPQzcnBz0HUa0gmjl4+G7xFfyXdT1CaZAOg/9zjoIcqcBEPy4GBlXpvjN8uqghgq4uWkFH8nHj/U+0GW2h6JHvipyU9YsHsBwm+E4981/w2XYBe4BLmI8qKPl3kyD5Iel+20iUfdWD+/M35CGqOcRsnKgESZ8ixFFC4n6uSnyZKepwjoM/ZL80Ov8b3ER05MOUFTXRLTIXOHCHlxec/VgtcJLyFe9g2uttzi3TBj6wxpS24uuga7yoS+J30PXENdpczgC8FCsKxTxNUIqRv9uhEnIuSECNUr3RJUnTzhoerG+rEt2ffY9sp3nvI4Rchw2KJhYiPVNsO4SUmXldrkS32eKqsqjgtOLoz3uz/+TlQ0N/y4QrSfaC95sP4kZroaWC+6pjhJTF0/VSY7Ch0KBU5eWXmGVaAm3srMoqWwrSjiZSPTN0j/HZ38XM5REYZeDZXOyV1/Hnuhz27/qf3Siak+OHiFhG9FifKkAus6uKukpT+RZMQOTmLgbi8HMJfSXHZSHXLTiXG4scZOqEiN9pB4ucxmPKoW2sQyeXKCg5E+s4GzB2L29tmy7D2YdxDDFg4Tl8DoFaMxcc1EzHOfJyp5/OrxooR4CoDqSw06Eo6FvYVMICyLLgy6BUYtHSXEFXY1DHaj7QQTujASHxt2rlWdAi4FiEuBu+isI/2m3HGnMqf/jvmnPk4Vf2ibnm3EX8iNRCrEQy8OieKmUuWgDDwXKBuZ3KTjcnbG5hmySUVXBX2FXGbTnUDVzfw3xm0UVwnbjXVydHKU5bDCnHGID22iAqevmeTA+pJcmY7/zI9Kjb5g+typzvicdeRKhMqONtOdwrzosiEhrziwQoiMkxgnbuLNzSLe056kp0nSHqwfVSX9/YxLkuWmH/sZlT4x5uTLsnlShTimv0jHQs+F4uIYs2KMkDL94iT5Jd5LBAfiQQxYXuyDWHFdcDLzPuYtpEc/NhXxoDmD5JQBJ2FOvqpurB/LZb2IPyd+1pf4cb+A/Z820lZuxHJSZP9i2zAd+yonxjHOY2Qi4iqC9WR6/sfcjZFVD7Hl8+g70UjLS5M2YT/jBEB7OEnwPvBKoExIoddDBQNNvKUgt8qcpCjiZSdkQ3NAsROwU1Exkfy4/OdAYhhf2Tl5zw7MTs/BxDQkZnY+LmUZrtIyb/XP+Pxn/vxnWoapzqpcDSq+GtQqPstUdjKMz5kfy+Jz2qHsUs+ZJ+9pt8pXvap8Gc5/DigOfObBdMxX5clX1t/YRsZXdWCevFdxWCchEaQX5MEyWCbjMK3Km3gxjH5Eumh4HInvFYbKTlVf2sC8WSdlD21mvqpuR/KOyGkLEg/bUuGiMCVeTFs4b+ar8lTlMK2qn0pH21T5jMc4zJv3/Kctqn58VXUp6jnzZnpFaNz4pE+cRMtNV66UQq+FSh7ERdVBlcd0xFBhwjjG9WX+tNW4bgon1Z+UfbSd98a202bGUzgwLeOxfGUD25tYqjCWZZwH3zOM8Wkv0/MZ81T3DDO2S7saKjOTltC21xGvavDSvLKj0/fGo1iq85Umn+qahgOdZ3l5ooG72xzEHOilxYMDmP5DunV4TrmoSae0eb/vdMQi5EqIqNZWnVqhabum4ic3Jr33bUNlyJ/tr4m3hORWmaOTeEMuhMisW1YdjJ2Efk76Ad+FMMrKnqqWDzGju4JKl6RLRfQudWB+POzPDzAwv3fJqyLSknxJtMHXgwWX6jiZsw9EPdEfGa7MXFoi23Kf5yL4eDDCH4YjPjcecblxZXIlIAHxL8ouv7Kyq6rkQ+wSkVhmGLI9mF9VqX9hO4lHEpLAehQOqw7vOTb9LvvhyKUjJRrfVTFytfjIMBvm9v3biD0Ri8jjkYg6EaUvjYHuA5WsD0Qcj0DmuUzk5uZWRS4tkc3VhnhLhIqOrBHQCGgE3iMCmnjfI7g6a42ARkAjUBQCmniLQkU/0whoBDQC7xEBTbzvEVydtUZAI6ARKAqBiiHevLyibNHPNAIaAY1AtUCgYoj33BUgIRNIydLXmzBIzASu3aoWHVFXshwQeJ4L6KvsMHjxotSNVjHEe+wcEBADhCbo600YBMYCF6+WunF1Qo3AKwgcPAbEpAHxB/X1rhhEpwEXr70Cb0neVAzxnjgPBMcDkSlAZCoQkVy1LrE75d1sjkoFeBnXnfnyGV/5PCQBuFT6xi1JR9BxqwECXF0FxwFhifp6VwyC4oBzl0vdaSqWeI1Jp7LchycBsRmGi/fvw66kLDwNjsML5p94GOBrdDoQn4kHB6KAhEMAZ1RNvKXu2DphEQikZhtWmMaTO/u3mvB5L2LgHUXF+xgzReVZWLgUFac0zzj2CufNZ+oiXhyb568UAXLxHlUc8cYehN88J0zt0QdIzHqp9GLSXyo+VlQBR2WswGDFjeOpOAoY9Z7xeal8mI4Ep56reMbpYtJxcY8/Tu/yMZAv4zBclZeUjW2TZmLvrEUGu43zYP4qvrpX4eo1LhPu0+bBtpUZepi0QaTzOiA5G49C4jG+e0/YtjbH1J598DQ8GQhL0oq3eP1YxyoOAvnEmxuWgDwjUcH7XCrAiGSDIOB97MH3Kz7UeHjdK8cPBcjrxlFEcoHNBRzxuryK+5xlJWXhQUAUnoXEG0QR00al4kFANG74BOOGb4ghLDSxihJvwmFsmTADvUwsgOQcQ0eITMGVvQGGRo9MwcOA6AKyzYtINryPN6jBS3v8DWQYd9BAdklZuLUvDPf8IwsI8UV4Ip6GxOGmb4ghz+h0XPUKFCJ9Tt9qhAHoO/vDcXd/BJCUjReJWZjp0B9z+gzCU5aVnC1hl2lXfCaQfhxLBo3AujGTgeQjhrLDk3B3f7iBoGMz8CQ4Fo9oOyeU5GzJV16Tc8B8ujZvjWu+oTiybQ9MatVFXnwmnIePwSRbBzxIzsawDl2xYewUgOVrV0NxKEXHKQ4C6eyvKRjZqTvS1+8w9OfEwwhzWo0xXeyEaKf17IsLe/xxYe8BHN+x1xBHCR6SEEWIIkOKEQoZY2Jj3JiMl3EYN4pq0UhQSTqqSqO8VLr8sjjeU9ZsNZAc8+DFlaiIpHQZ62O79RCSLBBWTJufvkAAGdv2tvv4TGwaPxVdmrWCg5mVQRRlHMehTW5o+uPP6N7SFF2at0bq2m2G+lRJxRt/CDsmz8YAqw5CTOwMY7raiQoc0ak7nobGY6B1B5zc6Q0cPIXVo8Zjx+RZuLo/Ar3MLNGrjTX6tLHGJa8gIPUo1jhOhE1LM9i0NIXP3KVCkGyYri1MsHjwKNz0j5Cy+lq1lzhTevQGDp7ElgnT0b2lCWxamcFz9iI8j05D859qoeH3P+KidxDWjZsKezNL2LU2x7huPfAiOQerRozFpvHTZMJghyBxjujYDbumzsGzqFRpuFPuvlg6bLTY2NeiLXq3sYar40QJfxwaj4fhSdgzcwGGtOsknZt1Sl6zFcg6i/BlrpIOsZnApevFGVI6jkbg7QjkEy+JJW7VBoOiTMqS8dKthQkQl4mzHvvwMCpVVqIUILfCEvEslPsxBlJ7GBhtIMOkbFzzDsINnxBRiUJ0FCYRyTjr7msgwLiDEpcuNcZ9FBgjY51pROhEJBvyYrrIFEM6EmxSFs64+6Jdw6Y4vn2vIf+oVJza5W0QX8k5uO4TDNvWZrh3ILJgMrh/IAoiqITsUyVurgisZIM7j8RN1566KGwUGcdnImPDThFC1/zCcHb3fuGJu8Fx2DpxBlYMGw1kHBeMJE2VdTUYE2/KETSr+Qv2z1+GFylH0KlpC2Ru3IVlQ0bBZeR4IVES3xk3Xwy27oiN46YCh06LShzTxRYHN7nBvG4DPAlPxh3/SFjUa4QLewPAzuQ+fR5w+AxItAv6D5V08/oORm9zKxzb6Q2zOvXxICQeD4JiYV6nAS56BUr+m8dPB+IOCqE/Do7Do9AEtPy5Ni7u9se6MZNeEi8bLj4Tx9180KlpS9i1Ms9Xwzk477EPR7d74th2Txzd5olLngcMs3xyDgIWr0Tdb77D7N4DgZQj6NCkudQZaceQ4LJJiFoUwWVNvG9nFB2jWAjkEy/HUsLqTQXEu2/+MtibWkp/H9e9Jw5u3AWLeg3RulZd7J4+HxNseglZPQ1NwEDrjrjmFYS1oyehZ2tzcZnxHqlHcNLdF71MLdDHqj0Gt+uMO8FxSFu3HVb1G2OQdUfkbN0Nj5kL0L2FCYZ36CpjL3vLblz2C4WDmaWkG9S2I64FRGPffCd8XpjlPwAAIABJREFU9dnnMpaOuvnAwdwKA9p3RrtGzUSJPgqKkWcFxJuULcJslsMA4QuunIe074KHQTEGYo7PhMf0+SKiOPYpplgv7rWISk7KhtesRXDsYgvknBee6GfZDsmuWyQex/aILrbYRO6hoq+yrgZj4k3MQk+TNrjkGSAqlMqXyx8S15B2nXFww04Mbd9FACJB3d4XJmqTvtjB7TqBJPnLv7/BsM7dBWySKdMQRDY2yczOxByHN7sDGSeQvcUD03v1w4EFy/Hzl19LuqEdusCkdj2kb9gl+a0fM0VsCXVajeEdu2FEZxs0rlETV7wCf0289Jdln8N0+374429/Z3AtxGbAd+4SuI6agDWOE+Q1ePFKg8uDvqvYDLyIzUDbRk1FffS1bCczLu2Ldl4nHUMaWBNvsThFRyoGAvnEy/2FRNfNBcS7f8FL4rVtaSbuPrq6uJdBdxddY/RtUhCM7mKLlLXb0KFxczyOSML94Di0qddQxA/H6mauBLPOYtlQR8zpPRBxqzbCrHZ9vEg4hLPufmjbsAlu+0fiXmCMCA+6PCieXEeNBw6fhavjBIzpYoO8iCQhefqfY1ZtAMchBZTz8LHob9VeXIhcRRYQb2wGznnsQ4fGLZAXkw63qXMMooauPoqjyBRxT5z18JN4jEshVODrZvo9/jCtUx975yzGgYUr8O3f/yGrT49Zi7B7xnwc2uUj9ZbVblxmFfXxxh/C9kmz0N+yvfhC2RnOuPvJbDWyUzcELFwhJMkNJzay9+zF8r5jkxaIWrEWOHVdFPJAqw4IXboaHZq0wN3QBNzxj5AOc3NfmJC1kO3BkxjcthPcp80FztzEnhnzxY+auHoz2jZsittBcbh3IArbJ83E7aAYWVZwA+zcnv2o/dW3uOAdhDuBMTJDcwlExSuqOznH0KhxmbiwN1Bmf7tWZgb/bPpxeM5cIHmtHD5WXoOcXHHCzVf8x0jJkfq0b9xMZlX6lLmkwblbWD7UEdN79QUSsrSPtxh8oqMUEwESb2SquM2SXLcYltzJOfBfuAJ92rQVIu5lain7EBQL68dOBo5cwOKBw4V4lg4eKYJo55TZmNdviPRfuus4RtePmYTOTVuil5mFuAipUKfa9xPiErfe4TMypumSo2sQaUcxw6E/IleshWWDxmIT1TTJdGz3nrh/IFJcg48DY3FtX5jEpRrm+Gce3Lt5hXjFRZGNUZ1sELbUBZPsHJCxjn7sfHdCbIYIGqfBo2QlzVdOEs+5iab8wgmHcGKHl9Rnx9Q5Uo9wEn7WWRFvrGvoUhdZLSPmIHCh9GfsK+5UQ/whbJs409DgiVniFjjt5ivEO7xjF3AWpop0mzYXf//4E3BpwSU5TwFYN2iM8fb9YN2gCRLXbEFewiHZMGCD0D/MGfFxZIrMmJkb3STdaQ8/cYxP7j0AlvUboZ9le+Sl5IBLK6rdUV1spSGfxGZg3zwnmfm4zOjSvBWm2PfD7N4D8PO/v8bhTW5YP2aygVxJvFGpeBaTLoqdxE4fb7OaPyN9w05Dx0w9IsswLsW4wfYwJB7sQIPbd8YAq/bSQbgJd9LNV1wVo2x6icI4z808+tX05loxWUVHeysCaTlAwmGM7NgNCwcMBzJPyf4JiVNOFyXnoEfrNkK8zsNGy0YTl91HtuyW8UlyfhqehNAlq2RPRAg0KUuEUbTzevRt01aW6y+SskTphqxYK0RNEuRKjiKIxCmbZPGZsGrQBClrt6K/ZTvsmjIHL5KzkeS6GfsXLBfiJXnTjccl/8L+Q5GbdgyrRoyDvZkVngTHwd7c8qXipapNyhZibNeoKSbY2CPPeCMwNgMJqzdj7eiJ4r6ge8Rj+jyDT5jEG5OOc+6+WDRwuLgaXoQnyzg853kA3CuSlfOxy5jfb4hBFMUdqqLEG5aIm76hsvwgeZ3a5WPwt0Sn4dzufQbne3QaHgfFiqNddi65pE88LB0jcOEKXKdjP+GwwYcTky6NHeO8vuA9FbQ49OMyEbd6s8yuGbt8ZCanO4MuCHYC+ruiVqwzzHz5x8b47KZfqDjoAxc5y04vl1u3/MJk2cV7mSkjU/AsOM7gn2UDxmeKcqebpGC3VTnw+Zp/NC1m5XpQcdOPLPnEZ8rpC7oj7vlHSD7yIRNNvG/lEx2hmAjwOFl0Ok67+4Hk1NuinWxUc0P6Kt13MelCvDzVELTIGa1+qYOjFENpx2BZv7FsfvP+eVSqqEISJjeORdEmZyPWZZOo3rE9+8hKMmrVRlGZE23tDSd8Eg/Lno29qQUm2drjx39+KeMmc+tuER2GdE3gN3+ZqG+eIlg+dDQ2T5guhD2j3xAhfK6SOUYczI1cDfljKy8yRVap3DSnUCvYPCN3cBOPz9SVlP3y9EVUKp5GJmN0VzsRbNxw3zl1LpBxElsnzYR1wyYY1sUWPU0tcIW8Q4VdJU818JMfPGIix8GSDLuFrAwB4hlCEhTv88msAEACzN3JpCzDcTJFakxLEual8lGklngYQUtcpPGoeHlWNpP+3vzdVDkvyJ1OlsUymZ7v5ehK2suy1HEWkjMvxmX5jM8ljXG5xuHKRvXKeGJroXOKTMMjaOqIjv4ARTEZRUcrFgIkXi6t4zPlDGyCy0aIy4H9kWMlPEkEhmHDKQ0Z63fgGo9fxh2UUwR3KQg4RjguYjPkWBVPAsg44vOEwyJWIpe54ppPsIwb+mC5L8LxcmtfOLznLEbWFg8c3+klp4l4VItkziOdEctcDXHzxRTPzXJzjnzANCmuW0ShcuOM52y5x8MjowXcEJ2GZ2GJGGDdQeohPKHGXHFe88c7MTm5y9vAAUyXeBj0Dcc4rwPPQAtW/ORtlSReGl4cMMoiDgky/pB0hviVGwxn/7jBpYizLMp4H3lo4i0Wn+hIxURAfXKNfVWI8pBhg433qv+SgEnEIg7yP0HJcULRYSwmGE6xocSLSi/i4fDLuMybaaNS8Tg8SZbt3CjnKQenIaNkI0zKKkiXYbCFZfL0gMqfr7xUfiyfAk2VG5uBy14B6NyspWxkizBTYSV5VfU2zpvpWQdOCAqrKnucrDyJVwHPxlUfx1XPKvOrJt5iMoqOViwEjIm3Ivp9PmnSX8ozuYZPphmR/rvYFJkiH1wSpUrlSgJ9l/zellYTbxX7gp23NahxuCbeYvFJlYyUmQn4+gJPnxZtPsP37Xt9eHo64OcHPH9edPqinlY08bJvkxCpqqkgjft6WdwrFfy+SZe2VkniPXYWOBBtMJ4V0FfRGPCrM9/hyEpRY++DeHbtGrB9OzB6NDB7NhAcXLWqdeECYGkJ1K4NTJ/+a/K8ePFl+MyZQOFf3T17FjA3B+rUAebOBYr7wwKVgXjLgmArQx5Vknhv3zM4pvl9lhV58cTAjTvA9duGY1sVaUtRZdN5/+BR1SKV923t3r3AZ58Bv/nNq1e7dsClS++79LLJ//JlgPa2agU0bgwsWfJqvgxv2xZo3doQvmzZq+HnzwNWVobwJk2AFSteDX/du+TDQFBsxX8HNhUp/bV0CfATYG/6TurKGsbvyq5yXwv5uo5RAc8vXz+J63fOVUDJusgSIxAfD/y3/2Yg3GbNgAULgAkTgE8+efnsHX4VoMT2vEuChASDqqVybdoU2Ljx1dzi4gALC4OyZV23bHk1PDoaaNPmZThXAG/7e/QUuPsQuPeogq6HwKNneH75HLKiAnDreCbw6IlB/Ny4DVSl6/otg+1vw/w14RXzAYrXGFO+j59j7rxVqFNnORo0cIaLy2YA+rfgyrcNSlAal9MNGhgIdujQlwnp40xKekm+q1cDN24AdEdU5uvePQOZknRbtDDUjeRK269fB+7eBTZsAKhoW7Y0hG/d+mr4unUvwxs2BHbseBleVN1v3gRu3aqg6yZw5w4u5qTDsv1YfF9zCeo0mIaAkKCXbVmN7qot8fr778dXX3mLqDA1Bb7/fisOHkyoRk1fxap67hzwP/4H8P/+n2HDKS0N6NIF6NQJ6NcP+PlnAyl/+ilga2sIY3hlvbp2BXr2NPhp//Qn4P/8H4Oab9QIsLEBVDj9wCr8v/93g+vBOLxWrVfDSdQMr4z17toOw38wRY2658TT0qTJCzRuPBe3bl2sYp3x3c2ttsS7ePEG1Kp1RVxpdLf99FM6PD093x1RncP7QYCqln7dr7825O/kBNSoYVim01dKAmL4f/wH0Ly54TnVZGW+aLeZGfD73xtsp/2/+51B4ZJAGU5VwMlG+bQZlwrYOJxpjMOZrrLVu1kz5DX8EWaf2aFVW8DKErC25rzjgePH099Pn6nEuVZb4o2ODse/v3NGkzaP0dD0AX6stRgnTmRW4qaq5qZx6fy//7fh4ibalSvA+PHAqFHArFmcOQ3k88MPhucjRwKV+eKJDF6//AL87W/AH/5gUK729sCYMYbL0fFlOAn3448BB4eX4aw7lT7Tk5z/8hegd29DeGWs+5gRmG3SAV/UDkPrtkDNBmfR2mQCHjy4We06d7UlXrb0voX70OHzebD5bAkiV0ZUu8avchXu2NFAriYmBj+oqoC/v0EpUvUFBKinlf/VxcWgXlkfbrJx89D4b+XKl+HcSEtMNA4Fli9/Gc6NuJSUV8Mr4bsn929iTosVMPvHdPT6ZhaOZFRPsVOtiRc8/tnoCdD4OeBbCXupNulVBHh+9c9/NpDvH/9oOJLFJbVaZg8Y8Gr8yvxu1y6DS4SuBLoGQkJetXbnzpfhPFYWFvZqODfa6FJheoZHRr4aXpnfDQGeNrgJ2AJ4zedHKrP5ZWFb9SbeQADNADQBsLMs4NR5vHcEcnIMflFFtnzlMpzuhpJ8iuu9G/qGAs6cMZCl8sXu3v1qZIbTj8twHiXz8no1/MSJl+EkX34Crqr8PQbQB0BzAL0APKgqhpetndWbeCkimgJoDICnyfRf1UHg8GGAhEXXAj9wUJX+eKyLvlhukG0uouMxnL5ehm/b9uua0d/do4dhA41HyKrS330A9vmChwRcTT8fVL2JNzp/5iXxrqtKvVfbWuURILkeO/b6arwtnGd9jx9/ffrKGnIbQI98wUPP0JPKauj7tat6Ey+P7bbMdzWser9A69w1AhoBAPzt1u75xDsEQAm+4+dDwq96Ey83VE3ziXf+h9Ssui4agUqKAD+d3y6feMdWUhvLwazqTbxnAVjl+5vGlQPaugiNQHVH4HC+2OHeyuzqC0b1Jt5bADrnE+9AAC+qb0fQNdcIlAsCMQBa5SveleVSYqUspHoTL4+29M4nXjr871XKNtJGaQQ+HAT25W9oU/FWsQMZZdkI1Zt4ieSIfOLtAKCKnUoqy46g89IIlAsCPB1H0uX5ef9yKbFSFqKJd0p+RzADUAVP51TKXqWN0gi8DgHn/PHG00Sxr4v04T/XxLs4vyPQ75T04Te4rqFGoEIRmJU/3swBHKpQSyq0cE28/OAQPzLMpY9fhbaFLlwj8GEjwM3rYfk+Xh4pu/BhV/dNtdPEG5pPuiRflzdBpcM0AhqBd0KA3/7ID0/wexq4qV1NPy5MDDXxHgXAZQ8V78R36lY6sUZAI/AmBI4AaJM/1sa/KeKHH6aJ9w6AbkazcDX97PiH39V1DSscAa4uuanGUw3F/GHkCrf5PRmgiZe/bzk8fxZuC6CK/EL4e+oPOluNwPtDYGs+6ZJ4976/YqpCzpp42UoL8ztEawCpVaHZtI0agSqIwJx8gcNxVs1/V1YTL/uvW/7JBs7EVeg7pavg0NMmV1cEeKJhaL5LzxoAvyelGv9p4mXjxwFoka96napxb9BV1wi8LwSu5n8vCsdZNf7lCQWvJl4iwY8K81whj7kMApCr4NGvGgGNQJkgQNcCP6TE00NTyyTHKp2JJl42n/EyiBtsF6t0m2rjNQKVDwHjjbVdlc+88rZIE69CnMdb+CEKqt4q9IOtynz9qhGo1AjwO1Godk0AZFRqS8vFOE28Cuag/I5B8l2tHupXjYBG4J0R4C8J98wXNfxJ97vvnGOVz0ATr2rCMwAs8zsHvyqS53v1n0ZAI/DuCGTnf2KNp4aofPWf/shwQR94BqBvPvHyu3mvFYToG42ARuBdEOCXT9HNwNXkznfJ6MNJqxWvcVvyBy85K9PPG2UcoO81AhqBUiOgxhX9u+mlzuWDSqiJ17g5A/JnZpKvPs9rjIy+1wiUDgH6c+nXpZihn/d+6bL50FJp4jVuUXWel4e8HQDoL8wxRkffawRKjgB/ZUJ9Mc6ikif/UFNo4i3csmPzVS8/T55ZOFC/1whoBEqEwDIj911YiVJ+0JE18RZuXvf8TQBuBGwqHKjfawQ0AsVGgF90zpUj3Qyd9Ya1MW6aeI3R4D1/8JJfjM7Owp8p0cfKCiOk32sEiodAWv4HJvTHhH+FlybewpDwexoG5n9pjgWA04Uj6PcaAY1AsRBYk+9mIPF6FytFtYmkibeopl5r9DWR+nPlRSGkn2kE3owAN6Z5Lp4b1VYA+AEl/VeAgCbeAiiMbrLyl0jsNAMAPDcK07caAY3A2xHgV63yNANddtyw1i67VzDTxPsKHPlv2En4sWESLzuP/lWKolDSzzQCr0dgdv7pILoZ/F8frbqGaOJ9Xcv75Pun+GEK/jSQ/tMIaASKhwB/t7B9vmixAcAflNV/ryCgifcVOIze3ATQKf/Lm/l6wyhM32oENAKvR4BHMilYeFXzXxN+HUiaeF+HDJ/zkzbsPDzTq3dl34SUDtMIGBDgfsiQfDedKYDDGpiiENDEWxQq6hnPIfLnSujrpc9X/2kENAJvRkCd3eWmGscMf91F//0KAU28v4LE6AHP9PI32Ei8/AgxO1Ul+Mt9+gS5Tx/rS2NQ0AfycivJ0Zu5Rl80pVeJr2ULTbyvhSY/gJ2Hrgbuzk57W+T3H34lIwbeveoiYnovRMyw11c1xyByVm8EjLBA+PSeyMut4F9pPZX/YwI8CdQdwO33Px6qagmaeN/WcvzZErt8l4MZgKNvS/B+wy8mhcJ/qCkuJAbjYnIYLiSG6KsaY3A5IxYZ2xYhZHxn5L2oYOJdbrSptuH9joOqnrsm3uK04HajT7ItLk6C9xfnUloUImf3xZO7N/H0/h08uXtLX9UYg9xnT3Au1h/Rc/pXLPHyCBl/uYV7InzlV6zqv9cioIn3tdAYBfAomTpaZg3gglFYOd+SeOlieHj9Ih7dvIKH1y/pqxpjwMn3dISPTMYVqnipcNURMudyHhRVsDhNvMVtNP7yMH29vCrwV4g18eqJxniyrRTEyw9I0KdL3y6/l0F/sdRbWUUT71shyo9AlUu1q5ZSV4ubsGzjaeLVxFuYeM9E5iveitpc4xdJcfOZipenGvTfWxHQxPtWiIwiLDVSvS5Gz8vxtjIR79NbV/HszvVXrqe3r+HRjctl6v4oaZ4sn2me3r5apnaQ8J4UUeeyrq8xsb7tnopXiHdW34o51UA3XNd8QaI/MFFsJtDEW2yoAJzLX0rxTC+XVHxfzn+ViXhvXzyDa2eO4+rp47h65jiunD6GWxfOAI/uAA9v48G1i2VCfLcunMb9qxfw6C2+XJb3/M514Ml9XD93ErQPTx8IAZeFLSTYu5fP4erpY4Y659f73pULZT7ZvI1wVbiBeH0RKcRbAWd51xn5drXaLTYbaOItNlT5Eal06eflsqoCvjynMhDv45tXhOC6dGiHj//8Z3z217/K9elfPwEvc5NWSI2NRN7D2+9EvM9uXxOCa1C3DkL2eSPv0Z035vfs7g2QpPvZ98Q3X/0bP3z3LSaNccTDG5fxpATqV9VPkRtfqXR5tbW0wJ8/+shQ308+waeffILo4APIe3T3jbYZ51WW98bE+6K8P0RxMf/LcOh+swTAc7z6r1gIaOItFkxGka4B6Jj/STae680xCiuH28pCvLl3b+D7b7+FVRszRIUE4ID3HgT5ecF9+2bU+P47/P3zv4nqfHbnmhAS1SrdEi/u3xQCK0w+VJPP797Ai3s3QeJjOONfOnEUn3z8Z/h67AQe35O0ufdu/orkmObZvZswN2mN7775GkkxEYgI8sc/Pv8co4cPlbR0PzB/Y9cAy2Q5yh6GUSlfPJFT8Ixhufdu4FRWBj766L+wYvECRATskzr7e+3GpRNHiqyTyvN9vr4k3j4od+JVP2RJEaK/DKdEo18Tb4ngyo+8NV/1ckNhamkyKH2aykK8JCwS7LhRww2VeXwXeHRXvvE6Jy0Jv/nNb7DP072A8PD0Pi4c///tXQd0FdXa1bfez3vY8QECT0VAROWpFAGV0EXpRUBAUaoICb0JoiAldEHpLUBAaiD0EkJCOr0GSCAFkpBeSe/7X/vcmTBcEkhu7r3kypm1zpp7p5755sw+39lfOTdw/fwppMZGAJnJAtgEPXAvThx3x88XNy6eEfwsr0WNNzLoJmq+VR2Hdu8AMlMRcycQwdev6GgMDZdM8AwP8EOLZlbwOnGsIHv9iiWLUKtGDWQmxggwDfS9iJx7sYK2IIBHBPkj4OqFAjAmuDv8tQktm1mJe1DLJXBy++E9u1D3vXfF7/tvMEt0FMagMgwBaAG8HqQazAy8apQaaTemgKT2K5diS0ACb7FFpTkwGQDzjHKIxXJOs8/EP8sa8P48cbzuifMygfws8fvoXgcBvB7HjwDZaQLUxtgMR513agsKoGH9etivaLCkB+LCgtH/2754953aeO/dOvjskyY68MxNR4QKvARxAL/PnY23qr8pziEw64MVAZDab35qIhIiw9Cp/Zfo26sn8vOy4O50GC+/9JLu3shHiL+voEaWLponOgKkMsY1Hw5bdFo7r0GOmJ0MctKwwHYmatZ4C2NGDEfzpp9h4Hffwv/yOdHhpBmJz9Z/nsf9f2LAO0vxZCDtxqmy5FIiCUjgLZG4NAc7KlovfReHAsjQ7DPhz7ICvKQaPmncCI0aNMC0X37GzxPHYc6Mafhp/FgBbv37fYMsAlZ2GkbbDEODjz6C36VzAhQ3rlmJqlVewwVvNyAvEz27d0Xb1q0Qcuu6ANK5M6ejRvXqCA24IThbnca7E8hKh9+lszi2f48wtmVoNF4VoEgnEDB/+WkCKr76Kl6rXAlht67rtNSsFIyy/hFvvP46YiPCBBfdqnkzZCXHC+32vOdJXDrjjbkzpuG9Ou/g1ElnUW5duQDkpmPYkEGo8lplzJ7+C7ZuWIfPW7XEf6tVBffnpiQ81AmodTLlWge8B82r8XpplA56NMhc1SX+4iXwllhkyglU7tS8o+z1Nxp6oZKdV5aA1+qzTwXwtGvbBs2tmgott3z58ti1ZRPyUhIEAJIqeO21ypg25Sec9nCFy+H9OOvugupvvoHxo0eI4X/58v/GisUL4XPSGa5HDgj+9KWXXsTShfOQGR99n2rIuKfTPjOSi/RwIEfLwvts27QezZp+KnhfeiPkpySIaD/SCP97/11BlZD+YOcQ4ueLD+q+j2pVq+DVChVQ7v/+D9WqVkWlihVBbT0/KxX+l84h0PcSkJsB5GeK53v3nXcwbPAgIDsV6XHm9zEm8IZ4KMCbYwavhhQAg5RgCXK7nKlFLiWWgATeEotMc8JVZVJM8lwdzZNAp6wAr8rxThwzSieQnHSc8zyJalWq4NfJk8TQPD8tCVfOeOO58uUFyDVqUB8N6n2Ej+vXQ+OPGwoj1VkPV/yrXDk0rFdPbBf7G9RHk0YfY/O61UiJDhcGMsHxZuh44cI0SFIM5GNJCWSSakhJAJArtNF//OMfcNhqr3CzOTi0e6foJGyn/yLqTsNfclQYgq5dRkTwLdEJEIQDrl4U28gdE8yBbAHSvBcLkAXroUOE5k/3OdUoWFj9TLXtPvAORl5OtqZxmugnaQUCLvPtThQiNtGN/t6XlcBb2ve7QqEc2BDHmb4hliXgrffhBxg30kZogAQdTsf8l91aAWrUepkFO+Dqebz4wgtwPsT8mtk6UExNBA1bpAS8XY7h+eeew40LZwpAkyBGf1wC6QPGtYxkAW6qp4QWzLLvxYKGs/mzZyD+7m2hGfMeBMgKFV6B3cplgoNOj49G6xbN0bhhA9Sp/bYAV3YQvBbpEz7Dtg3rUKd2bZ12nZ4ktidHhmLS2NE4cXi/4H1Jc/BY0iSdO7QTvsMEZ22dzPH7PvAOMT3w0oOnk0Iz0H3sVmk/nqf3fAm8pX33NLT1VxojNQFyvyZcyhrwjh1hDeSkC8AR4Judio7tvkTlSpUQd/cOcjNShYeA1aefIE2Acx5u37gitMTdW+2RmZKId2q/LQxgeQy8QB7Oe7mh/ocfwsv5mAhYuO/VkIKkiBDEhgQ+BHAE2aDrl/HMs89i+s8/6bTTvAzBx1Z45RUdRYB8sL40kCXHRaNH186gj3BeaqLwehDgm5oofIaH/zBYgDafiSCbl5aEFlZNhfEvhV4OyBXHlStXDru3bUa+4qVhDrDV3kMAr+chuM80scbLmSQmKJouqTV7Ezbyp+DSEniN8ZI9NbNUdDdtRFtZAt63a9XE8CGDhMarggG1Rw7R6U7Wr09v5OVk4uaV84JiYFBDx/bthOGsXdvPRaRbflY6vF2dULtWTXFM+y/bCt6Y56bFR4uIuEoV/4N9O7eKN/XnwnnC+yE+LFi4m6n35ZouXzs2bxA8bcvmVgLwafzSnZuH3X/Zi3o5H9wrAD705nW88MLzmDx+jAiAEBqrQlmQqtBeOyclHsE3rqBRwwbCpazdF21F8Mi0KZPAZy7M0Kc931S/7wOviTXePYoXA2djGQYg3RgfztN7DQm8xnr3thrKYWyBG6mxrl5wnbIAvAQoaoIHHLbjtNsJZGkCEAgwpBBcDx/AFrs1SI4KFe5WDKt13L4FfyyYKwxfInDhXizohkWfXYb4bt+0HgRWbxcncQ3SB9RwHbdtEVpyVnIiLvq4Y+uGtYKTZR30AY3gS4167fI/YLdqOUJvXhOuYqyj035H7N+5TQRxkNclYNLnd/s/y944AAAcGElEQVQmO3EdLVWg/c17kLLIT00Q992zbTPogkbNnPcrrB769TLV//vAa0KNlxQDqQXaMljOFzRH+cNACUjgNVBwD51GepCp8ejXy6EYY9hNsJQF4FVBhDkRCEYEJXWbuiYgMWiC/7mfCWsYNEFagkCrD1YMgOD1xP60JGHM4nkEQF2+hRikxtwV3DD/6wOjel+uBVebnVbgg6vWQfjpZurqVLCN9EYJaAK6q6nPwQ7mUfXQ1slUv3XAe1ihGnR+1EZtdpyBhRouNV226zVGvfpTezEJvMZ89acV4P1SWZ8y5sV11ypLwGsqMJHXLb5bmgBeLxMCLzPyqV4MdGAxk7+68b+csnVFCbzGfh/UdJsrwEsNmLkdjLhI4C0+KD0NAJ6VkogQFXizjazxOmtsF90ABBmxIT/ll5LAa+wGwLY/RrH+UlP4VUShGu0uEnjLFvCSK2bghFjztzmKJlCDwBtqCuAN0cyhRlfJw0ZrwvJCACTwmqIZ3AFA7wYaIsiLMamOkRYJvGULeFNiIvAkChMNUaO/D7yDkGcsjZceCyM1ysM8IzVeeZkCCUjgLRCFkX8wQRazlzErPw1ubsa5vj7wUsPKijd/4X2fhqF8Uc+oPv+FgAi434iAl5/5Cu93924EMuMiQE+PUK8jcJ9pROCdq3EdGwCAuYPkYlQJSOA1qjj1LsZJMcn3UvMlRxagt9+Av1rgzUyIQkJUBK4GRcDXTIX3uhYcgaRo3RC7KGD6u29XgdfbPwJHr0bguK/5Cu8XEhaBLBV4vY/AbeYg5BpD46W7NEdpbLMctZk537QBn4RFniKB15SvjTlLyPGS66U7DpOLlFJ70AJvVkIUoiN0Hz4/xmNmKLyPk28E4qIikKHhGv/uQKv/fCrwnrqpk8eJaxFwuxkL91txOHE9EvzP4nojCh4B8XD1iy7Ypu4rztr1RjQ8AxLgIUo8XK5HCvmHPgS8g0sPvCcVwCXoMuse/8vFJBKQwGsSsWouypDiHzR8GYE4V7O/hD/1gTcmIgLO13SlOB9yaY/hvVyuRyBeAq+gWlTg9Q6+h11ul7Hl6CkBlARI95txcPYNh91+NzhdDoX7rXjxX/8d8Fj9bfzvciMKRy/ewcaDHljr6IINB9xx7HIIjl+LxIPAexRuM6jxZpawNWkOp2bLeQQJulQUtmn2yZ9Gl4AEXqOLtJALMls/pwtSgyuYWMfApSjgPe4bLj7sM6HpOHUnRWhaJ66FF/pBF/aRcxvB40xYOryCEsV5BI2TfjE4HZomykm/aPA+Enh13gvUggm87oFJ+GXRKjRt0x4dv+6HET/PFjI8dDYQ3b4ZhE5ff4cOPb7BHs9rAoz15X/SPwbUbPW3nw5JxfgZv6P+J1biGt2+GQhHr2tw9Ys1LvAy9cR3ipZLmmG+gY1TnlZsCUjgLbaoSnkggymoTTC4gkY3A5OMFA684WIoutX5LIaO/xVTF64Sw93CPmb9j1v8vx4phsML1u/E4NFTsHLnMaG1ceh86HwQRk61xZhp84X2ddI/VgKv4jJG4D0XFAsHz+toZNUKW53OwudOCrr07o/Vu48LmQ0YMRG+CYDNlFnoP2Ki6BTVd0BNl53kzwtW4I/N++BzO/kB8PUMSkKvAcPx518HcDo0VXSKOqohvHDgzTJA440FMEQzImOGPRkkUcqP/fGnS+B9vIyMdwSTRpPrpacDfSN1eV9KdP3CgNftZhy2u1xEk2ZtMGXecvTs/yMGjJwEr6AkwQkKzdU/RoDCCV+CdLzYx+0EAX7wU+YvR4svOsF25Wa0+KIzlv51UIBC174DMWTsVPS3mYCvBw4XWrXrjUhJNSheHRdux2HjYW80/7KTGDH4JQPf24wXoNtnyAgs3uSIC1E5WLPnBL7s1lvwwC7Xo0TH6HQlDNR2+/4wEpNs/xS/1XdCTvj41bto8EkztO/RF+2698GU+SvgEZjwMNXgQ6phIHJLCrxMWTxcUQTYHunBwGyXcjG5BCTwmlzEejfYoXBoBF9qvrqpxPQOKvpvYcBLLfQvpzNYvHEPbqYBdgfcYPV5h4KPnNzi+n0nMXH2EpwLzxKc4+R5y+AmtFcdF/n7xt3Y7nIBIbkQmtnY6QsEX9mqQzecvZshwLlNx6+w4aAnPAPiJfAqwHvmVhRO3IhGlz790WfwCMxabo//1W+M0b/OFR0VOzDSN3YH3NHuqz6CtyXwslP8c8t+fN6pB2q9WxcfNGiCjj2/xQ7Xi8JAR6Mc+dzpS9bB/rA3drhcRMPPWmDxpr3wCEx6UOM1BHg5LynnKVUNv/0AMGhCLmaRgARes4hZ7yarFTczTg9PDbgE06cUBrzkXak5ESBnLN2AmnXex7Tf14IcITVa7iPf2KR5G9iu3IK2XXpi5rJN4uPnfmpZ1Hq57vn9UNSt/zGOXQrB/HU70GvAMJwKSYXP7Xvo0mcAFto5wCc4SQKvArzkeAm8h84FYtyMRZi1fBMGjZqMqQtXou+QEVhi74iLUblYvdtZ0XjjxCiElAENZzS69Ro4HON+WyiAllqw6hXhdCVUUEjk3q/EAd9bj8fgMT/DJyRdD3iPlUzjZeIbzh5B0KXdoTeAQL02Kv+aVAISeE0q3iIung9goQK+aoAFAy6KsRQFvNRevYOSsOXYaUyYtRhtu/TCwbOBwjhGeoEf79bjZ/HSyxXw44TpOB+RdZ9P9A0voB5W7TomwJdAsNBuF3oPtC4AXtIO3CaB975xjRrv4Uuhgt7Zf8pfyLllu65iBEIZfj98HC7H5gvufcCISXocb5SQ7bTFa7Fsm47aUT0c6BFBLbdFuy7Y631DuKM1a9tRyN8j6EGNN8xHBd5ikLOMSpuqgC5tDkz3yCms5GJWCUjgNau4NTejSxmnyGaAhQq+hzT7i/hZGPC6+scIUN18xAeXovNwKSYfjaxaY8WOo/AMTBSa7KmQFKzb64Kqr1dHv2FjhZeC+pHTCLfawQlHLtyGfwqE+1LTNu3E+R16fivoCRp32nbuKbhKr8AEqfFqNF73gET8umgNWnfoLmRESodGtsPng/BVvyFihNH56++x18dP0D+qcU2sfcPFNnqMaL1Q+G7oEzx62jy07tBNUBLWk2eKbfruZMUGXro2cnIOUlw08nLE5VNEQ5ObTSoBCbwmFe9jLs6EOvTrVcGXTuucHOERS2HA6xGYKDwRPm7aEsu2HcL4GYvQsl0XHL10B/yg6Z2wx9MXjZu1xvq9rsK1afzM34V2xmEtQYLD4869v8emQ57o2Otb2EyeJUC7TacemLpgpeCHaeA5cS0SJ/2iJPBqgJcBJezgdntcFb685G8JqpQ7AXTzUR84+94VoKkazx4A36L8eK9HipGIg9sV7HC5IFzU6NvL+2n9eMNOFUPjZeAOkzeRXiDospx4REOTu0wqAQm8JhVvMS5O8J2jfBDUfMn5PsLgVhjwMqiBkU1L7Peie7/B6G89QYCAx614AQAEhYXrd2HSnD+Ehd3+iDeGTZgm9tHQQ0OO89Vw0KBGI9GkOX8Kv1ICyHbnc+g9yAbfDB0FB/crcLvF6CkZQFFo5Jp/7EMaLWVLzZXrB8BWiWwrzjYCuAriPP5h4HXScbyZRVANTE2qei+QXugAwLUYbVMeYjIJSOA1mWhLeOElGs2Xrj2cpLeQpSjgJfgSKGkkowarRk3xQ6WWRQObV3CS+M19DJIo0L58wwUw8FxywVwLMBZBGXHiej53ksU1ZQCFLjlQYcBbHBA1xjElAl7OQk8/XdILNKSR0/UqpGHJTWaVgARes4r7MTdbrtF8+aEsfXjutkcBrzE+alIJj7qODBkuo8D720DkZurNQMnp1zkDNjty0li9AFx6TBuUu80iAQm8ZhFzCW7C3L38UMjBMXxzyoOzWJgeeHXJXYoCXwm8ZRB4Tx+H228DHgReJrj5SgFctifOhnKzBO1QHmpSCUjgNal4Dbz4bmVYSD6Omi+1lhu6a0Vc9hB8XlpsOJidTCbJeTJ5gVWqgWkhjygZ20gBmKPwftq0kGEK8ObkKxrvFk37oTFtMIDbBrZFeZpJJCCB1yRiNcJF3ZXEOjS2cZjYFYA7cO/maZyZ2x9ISxDAGx3+BNJCXpNpIdU0keHhOhAkEJqzMA9zemw4ctNTkHjlJE7N/QZIAbBA4y7GERO9ZjgDtlzKlAQk8Jap16FXGUYTMaUktZb2QNoXSVg5YBFsenTByaOOQHoiEqIjcSkoEpfNWK4ERSIpJhIZcZFI+5sVTtdenMLn5nFZ8ZHISjBWiRKdKUcyjysZvG9SHJJjQrDUdi5+6NYXu3rtBFrl6GgqdthMxF+KFKR6rVH+NaIEJPAaUZgmuVQSgBlAtlU6JjZcim8HXYb16Gh07LgGJ44eBHLTkZOcgJzkeNOUe/HIuRePbKXofschMykOGUm6NX+r/7ntsSUxDhkPlFhkJJqjxCAjUSkJMcgopKQnxKD4JRrpCY8o8dFIN7hEIT2+6MK6Z6dE4edJc9Crtw/G/ZSJDl13YMdH+4C+OYDbZQClLRdk1hyTfNRysksTidXIl80H/GZfRO8ujpg1D5gxAxj/EzCwywCcXz0cp/4cDZ9F+mUUfBbdL96LRqHQsnAUvDXFZ+Eo6MpI+Cy8X7wXjkSRZcFIeBdaRsB7QfGL14IR8Fpg83CZbwOvEhVreM1/TJlnDa8iy3B4zSu6eM4bDlHmDocnS8H/Ybr/Yjt/l7DMGQbPYpUfcXqpNXZN7oyeXddgti3w23Rg8m/AoJZLkX2Os62uVNxilgEwtDCu/ayRG7O8HCUgNV4LaQe3I2+ge3c7Abq2tsDQyQkY8/4E3Om7FUH7tyPQYwcCj+9AoJOm8P8DZScCj+9EkFqcdyLoobILQc5Fl2DnXQh2dkDwiceV3Qg+oRSX3Qh+bNmDYJc9CHbVFkcEu+rKbVdHPFROOuL2yb1FF7e9uO22F3fc9j2+uO/HnRKVAwhxV4rHAYQUlIMI8dArngcR8kA5hBDPIorXYYQ8qpw6gtArRxCx7hiuNLNHj+YLMWU2YDsbGD48GaPGLUMeogGsB8BsTGtKUejPSK1XLsaWgAReY0vURNfLRy7WrNmKHj12oXc/Z/RpMBdBVgG6KKTxAKjkyOXpkABzenwNoCOw56N9+KrVKvTs44gePebi4kU66tK7Ya0E3jLcGiTwGvRyaLGgCbm0hVlLsktUg0uXz+G463HErL2ri0KixwMNKfR6oA9wEVGjJbqJPLhsSoB+uExyo/p50+hqA9x28oeLpzNiYsKUesfrAe86ZcoThkPyt1YLVvex8XBaFK55HI+RGq+pGoIEXoMky6GcHYCNSiNlQzWksHH7G1QDcdJFxUdTnY5b+RBx3vBLyjPLoASowBIT2bmqUWjscBcDYN/90KICL90aNiIvbzU8PCbC05NJeNnm2G65XovMzBXw9p6E48dHw9l5DJycRuPsWUbtcD+5YUk1PCReI2yQwGuQEDk7ILUBzlpJI4ahhV/ONYNqUHASvR7+UCLdqPmyMNkOq8epXeRi2RI4B8BacSlkQA07V05M+cgkNyrwbsCtW7Zo1OgtvPdeFTRu/BZatqyDwEBmZSL42uPEibF49tlnUbNmRdSsWQnVq7+KHj0aKMDLGHYJvKZoQBJ4DZIqJ6Yi6JbWePEngOsG1eChk/iBMgMVP0z1A2XEG1P/MfG6XCxLAhxUsXmwE1XppGJ3qATe9cjOXo2PP66OL754H/furURurh2srVvAyqoWsrKo0W7DjBld0KpVHWRkrEFW1kokJy9Faip7be6XVIOpGo0EXoMkWxjw0pjBwgZbWClsvxGBl8+hDkm7KENSZqPiR8sR5mmDHlSeZG4JcASzDUBfJQJN7USp9RabQiLwbsLly1Px8svl4e8/EwDjiDchKekPvP56Bfj4TAKwQ2i3trbdkJm5AYmJTJGncr1UKiTwmur1S+A1SLJa4CWgqo2VRByLFoDV/eSA1f0qMBsZeNVnUY0wzPOgaktMusPwUV/1ILkuUxJgp+mozPSrpnDk6MUgoymB1x6enuNRpcpLiI39HcAGoQXn5KxCtWqvYONGDofs8d57VfHhh68Lrbd27cro2rUewsMZd0wqQgKvqdqIBF6DJKsCL0F1A7ZuHYx27eqia9eP4OjI8T5BlvtYNmLbtiFo374uOnf+UBgvdABM8DUR8PKZSC8cBTBU0ZwIwDTMdAQwH0CAQQ8uTzK2BHIAHAfwo+Y9EXg5Lc9sQyehJPBuQGzsIlSs+AJWrfoWwC4ADjh6dBSeeeYZ2Nn1R17eGrRp8y6mTGmHwMC5uHp1Jpo1qy244IwMaryS4zX261avJ4FXlUSJ1irwbhIc2XPPlcOCBT2xevX3eOut/2DRIiY+pRa8BcuX90Xlyi9h1arvMGdOd7zwwr9x4ICNst+EwKs+D93LOJ0QFRxqUKQf+GFTk6JiU0rbnnobuS6hBNIAHAEwUhmVqCMTvh9ORsloX4MXAi87/U1Yu/Y7PP/8vzBwYFOMGtUGPXs2wBtvVMDq1QRj0g+643Qa8VaEhs4D27OLC+cJ4j5pXDP4NTziRAm8jxBO0bsIvGsRHj4f5cuXw/btTPHvILQKd/cJeO21lxATsxiZmatQterL2LGD+5nr0QFz5nRDvXpvIC+P/pN01zGSca3oyur2kDv8S5nKmwDMD50ATA2YFAQ54LzHXUTuL7UEOPcZlU82CdULhWuORkYD8C71HQCowMtR1U74+PwEa+vmouOPjl4kNFoHhx+Rn0/qi+1Q9e1dD1IRtWpVgr39QGW7BF5jvBH9a0jg1ZdIsf4TeO3g5jYelSq9iMRE+nPRr3e98IvkNvpE+vpOQ+XKLyocG/dvwvXrv4ltt2/bKumjzAS86nNFKdGkfRQNWKUgaMRhBJwLAGpjcjGuBOiBSJyjKxg7PFXuXHMA5GTMTGIEXrbFZVi16hukprKDZ8e/D35+MwTvGxPzO86fnypczeLj6dbIEdpfCAqyxYsv/hunTtH4RuCWwGvchqC7mgReg6RK4F2Pq1d/wfPPl0NAAMm4raLhxsQsQrly/xRc7+HDIwT1kJ1NP19qFXaIiFggjBvUQnTuaGYGXvV5OQHidgCDFCBQtS8CAVNR0rbCtJRyMVwCmcpIgpQO2ScVcLmmaxibgFuJgxeLUR8C7zrk5KxFw4ZvCoNZdPQy+PnZ4qOP3sCPPzYTbTUh4U9Uq/ayoB8iIv5AQMA8NGlSAx07foC8POZ6kAEUxRC2QYdI4DVIbATeVcjNXY8WLd5BkyY14e8/FzdvzsPgwVb417/+KXhcB4ehePPNV5GbywgiHfBGRi4U9AMpCZ1G8YSAV31uRj0z9p9aF8GXoMC1alH/RdHGSFXIpXgSCFFoHdpZ6U2ilSmpHXp3mVSRVKkGOwQG2qJ163fx/vtV8cEH1WBt3RIZGWyPBNaNuHbtN9GG69atCpa+fRsjMZG2B3pBSK+G4r3wkh8lgbfkMlNylDKAYgPi4/9Aly4folatimje/G2sXdsPjRvXwP791iIMkxFBWVk8lg3dTrjqVK36Ck6fnvxkNV795+Y085yni9GinImWwKtyj1x/rxi5Gaacqn+y/A9SOM4ApgPorgFbgi75W/rlkpHyM4esVODVhQyz0791axbY6es8brSZyzi0WYfAwNkIC5unDHVIi0k/XlO+KQm8BkmXGu8K5OWtREaGDoDDwuYjOZnbVuG//30F165Ng5+fjs+lQUOnQdjj8uVfBcdLw5wu1PgJa7yFPT9dzfhtcq4uUg8ED3XNITLpCdKCBGpGWD2NC93AOIsvbaocFfTW8LbqiKETAFKlh809/Y4KvGpkJUdb1GAJqPRUUP3I1XVR+6XGa6qmLYHXIMkSeFcjI2O5sBDv28ewov3CgDFzZhfUrVtNcGRZWatRo0ZFLFnCHH40buzCiBGt0LRpLc1QrgwCryoTGtk499sMRYujFqwOm1UwppFumrDb6Gax/Tsb5jh3GfOCE6foBsYIQcqBhVqt6i3Cjon49sRm9dUHXhVgS7qWwKt+CsZeS+A1SKIEXhrMNmHmzK7Cs2HChHbo3/9Toe26uzNGlybszdi9e5gI27SxaY0BAz4Tx545w/E8gyzM4Mdr0PMVchJ5S2p3rDoNRSrQqHQE/5OioJZMhw32M1cAWDI3TPqA7l1UFMkMkS5QOVs+ryoDdRTAADGPskDFSOAtpAWXqU0SeA16HTqqQTdk24BDh0Zg6FArTJ3aQXBl9yPTqGHY48yZybCxaYnx49sqcfMEXe6zIODVyomuUXR/YpKrfkpQhqoNE4xULbCDwg1TI+YjkwPlNPX0qChLkzAyyCRcMXgdVLjscUqycbrZqc+jAi2flZ0MtV5qv+S9y5SmL4FX21zL4m8JvAa9FRV4yaFxTEntltEJjAQil6Y/pCPqcB8LjRnqfgsFXq3MGBDgo9hi6AdMrlNN7KIOwblWh+G06lNzJGhRM6b76DEAZ5ShOQGQWjI5VGMtBFbSBNTaGannBeCAUmfyswyr7qG4eKngqoKt2qEQaEkh0COBmj/53bLUeTwgKwm8D4ijDP6RwGvQS9ECrwqihqz/BsCrLz8a2xgFR0AlqDFggJqvCmgqkGmBjYY7DuFpjCKNMUBxbyOtQUM7DXl0KWU/x36N/dcOJakMKQ1m81KDsMgAUay0ZxIk2RkQWKmZ09uAdWHHoNZHrYfaObB+DNvlsaTuSR/Q3Y58bZnSavUFr/0vgVcrjbL4WwKvQW9FAm+xxUbtlVomtVp6StDdiglheioaphbw9EFZfx/3q4X7CJ6POkb/euq56pr8NMGeoDwWAL2tCOjUiKkdl2xWpmKLxPQHUr1nT8UeiAYyQ4ucZdhU70oCr0GSlcBrkNjUkzj0J0/MIAIO+Wm8omZJLpgAyDwG9JbopgAjM3VRI6YmqhrzCLjaQhCm5kxtlsYuarakB0ghEFipvdK1i0GG9ABkoCHDoznzEmfq+Fsli2eOSeb/LG1hpp6n1V9QbaymWUvgNUiuEngNEltxTmKiHgZoUGkLVrCDxiu6cZFLpnsbZ9Vgykt68NEYRkMfp8LxVGgOJgwnZjBY4a7CGTN8Vy5SAmVEAhJ4DXoREngNEps8SUpASkBIQAKvQQ2B42TGf5JHY7JoQwstQHJKCINegTxJSsCCJSCB16CXx3EwrTD0K6JZ3dBCojHIoBrIk6QEpAQsVwISeA1+d7TGGKsYXAl5opSAlIAFSkACrwW+NFllKQEpAcuWgARey35/svZSAlICFigBCbwW+NJklaUEpAQsWwISeC37/cnaSwlICVigBCTwWuBLk1WWEpASsGwJSOC17Pcnay8lICVggRKQwGuBL01WWUpASsCyJSCB17Lfn6y9lICUgAVKQAKvBb40WWUpASkBy5aABF7Lfn+y9lICUgIWKAEJvBb40mSVpQSkBCxbAhJ4Lfv9ydpLCUgJWKAEJPBa4EuTVZYSkBKwbAlI4LXs9ydrLyUgJWCBEpDAa4EvTVZZSkBKwLIlIIHXst+frL2UgJSABUpAAq8FvjRZZSkBKQHLloAEXst+f7L2UgJSAhYoAQm8FvjSZJWlBKQELFsC/w9aczYIBDL9jQAAAABJRU5ErkJggg==[/img][br]In die volgende oefening gaan jy 'n kans kry om funksies te evalueer.
Evaluering van funksies met waardes
Verduideliking: hoe om funksies te evalueer met veranderlikes
Kom ons oefen meer komplekse evaluerings
Merk jou antwoorde:
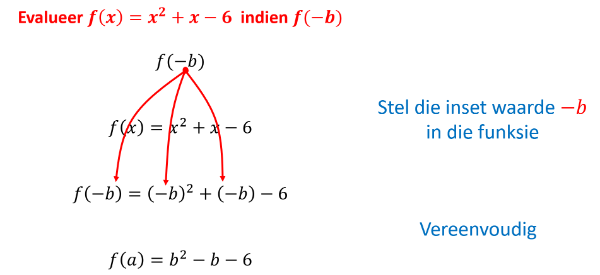
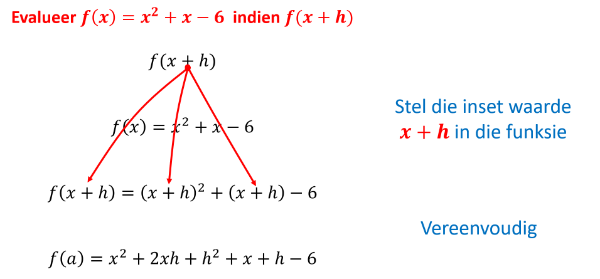
Grafiese evaluering van 'n funksie
Ons kan ook 'n funksie grafies evalueer. Die volgende oefening leer ons hoe om dit te doen.
Oefen die grafiese evaluasie. Klik op die groen blokkies om die stappe te volg:
Verduideliking: Hoe om die y-afsnit te bereken
Oefen om die y-afsnit te bereken
Merk jou antwoord: