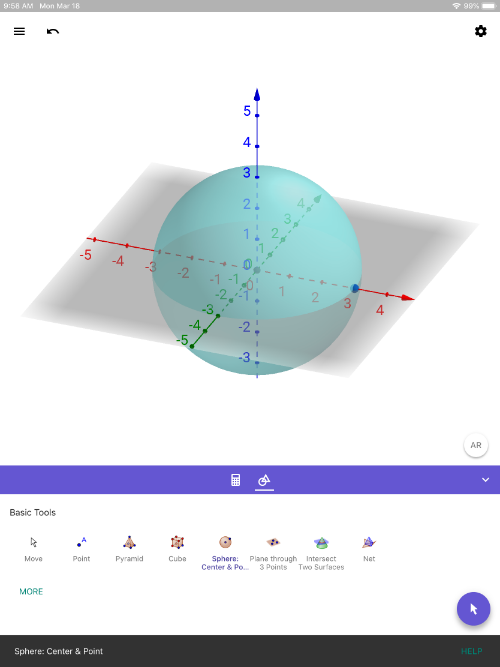
-
GeoGebra 3D & AR: PreCalc & Calculus Resources
-
1. Quick Intro
- GeoGebra 3D with AR (iOS): Quick Setup Instructions
- GeoGebra 3D with AR (Android): Quick Setup Instructions
- 3D to AR: Quick Method
-
2. Precalculus
- Exploring Ordered Triples
- Conic Sections: Introduction
- Parabola: Cause and Effect
- Baby-Step Modeling in 3D GC with AR: Part 1
- Baby Step Modeling in 3D GC with AR: Part 2
- Sphere Investigation
- Varignon 3D Action: REVAMPED!
- How to Create a 3D Surface of Revolution by Rotating ANY 2D Figure about ANY LINE
- Spinning a Piecewise Function About xAxis: Quick Demo
-
3. Calculus
- Surface of Revolution: 3D Augmented Reality Template
- Disc Method: REVAMPED!
- Disc Action!!!
- Washer Method: REVAMPED!
- Cylindrical Shells: REVAMPED!
- Calculus: Surface of Revolution formed by Rotating Area Between 2 Functions
- Modifiable Solid: Isosceles Right Triangle Cross Sections Parallel to yAxis (VA)
- Modifiable Solid: Isosceles Right Triangle Cross Sections Parallel to yAxis (VB)
- Modifiable Solid: Equilateral Triangle Cross Sections Parallel to yAxis
- Toblerone Warm Up Modeling Question for Algebra, Geometry, AND Calculus!
- Modifiable Solid: Isosceles Triangle (Modifiable) Cross Sections Parallel to yAxis
- Modifiable Solid: Square Cross Sections Parallel to yAxis
- Custom Solid: Changeable Rhombus Cross Section Parallel to yAxis
- Modifiable Solid: Regular Pentagon Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Hexagon Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Heptagon Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Octagonal Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Nonagon Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Decagon Cross Sections Parallel to yAxis
- Modifiable Solid: Semicircular Cross Sections Parallel to yAxis
- Custom Solid: Elliptical Cross Sections Parallel to yAxis
- Solids with Various Cross Sections: AR Templates
- Arc Length to Surface of Revolution: Calculus
- Partial Derivatives: Graphical Illustrator
- Plotting Points in 3D: AR Template
- Cylindrical Coordinates: Dynamic Illustrator
- Spherical Coordinates: Dynamic Illustrator
- Circular Paraboloid of Revolution: 3D Augmented Reality Template
- Special Hyperboloid of 1 Sheet as a Locus
- Special Hyperboloid of 2 Sheets as a Locus
- Ellipsoid: Quick Exploration Template
- Special Spheroid Action: Locus Illustration
- 3 Tori Morphing
- Surface of Rev with Helical Cross Section
-
4. Miscellaneous
- Shortest Path Between 2 Points on a Sphere
- 3 Golden Rectangles Surprise!
- Dodecahedral Surprise!
- Holiday Fun!
- Seashell Surface
- Dandelin Sphere Action!
- Modifiable Torus
This activity is also part of one or more other Books. Modifications will be visible in all these Books. Do you want to modify the original activity or create your own copy for this Book instead?
This activity was created by '{$1}'. Do you want to modify the original activity or create your own copy instead?
This activity was created by '{$1}' and you lack the permission to edit it. Do you want to create your own copy instead and add it to the book?
GeoGebra 3D & AR: PreCalc & Calculus Resources
Tim Brzezinski, Sep 18, 2019
This book contains Precalculus & Calculus (Calculus 1, 2, 3, AP Calculus AB & BC) resources students can readily explore within GeoGebra 3D Calculator. Directions to explore any resource within Augmented Reality (within GeoGebra 3D Calculator app installed on any iOS or Android device) can be found at the bottom of each resource page. This volume is a work-in-progress and will continue to grow over time. Wishing you and your students much success in your exploratory journey of learning mathematics! -Tim B
Table of Contents
- Quick Intro
- GeoGebra 3D with AR (iOS): Quick Setup Instructions
- GeoGebra 3D with AR (Android): Quick Setup Instructions
- 3D to AR: Quick Method
- Precalculus
- Exploring Ordered Triples
- Conic Sections: Introduction
- Parabola: Cause and Effect
- Baby-Step Modeling in 3D GC with AR: Part 1
- Baby Step Modeling in 3D GC with AR: Part 2
- Sphere Investigation
- Varignon 3D Action: REVAMPED!
- How to Create a 3D Surface of Revolution by Rotating ANY 2D Figure about ANY LINE
- Spinning a Piecewise Function About xAxis: Quick Demo
- Calculus
- Surface of Revolution: 3D Augmented Reality Template
- Disc Method: REVAMPED!
- Disc Action!!!
- Washer Method: REVAMPED!
- Cylindrical Shells: REVAMPED!
- Calculus: Surface of Revolution formed by Rotating Area Between 2 Functions
- Modifiable Solid: Isosceles Right Triangle Cross Sections Parallel to yAxis (VA)
- Modifiable Solid: Isosceles Right Triangle Cross Sections Parallel to yAxis (VB)
- Modifiable Solid: Equilateral Triangle Cross Sections Parallel to yAxis
- Toblerone Warm Up Modeling Question for Algebra, Geometry, AND Calculus!
- Modifiable Solid: Isosceles Triangle (Modifiable) Cross Sections Parallel to yAxis
- Modifiable Solid: Square Cross Sections Parallel to yAxis
- Custom Solid: Changeable Rhombus Cross Section Parallel to yAxis
- Modifiable Solid: Regular Pentagon Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Hexagon Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Heptagon Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Octagonal Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Nonagon Cross Sections Parallel to yAxis
- Modifiable Solid: Regular Decagon Cross Sections Parallel to yAxis
- Modifiable Solid: Semicircular Cross Sections Parallel to yAxis
- Custom Solid: Elliptical Cross Sections Parallel to yAxis
- Solids with Various Cross Sections: AR Templates
- Arc Length to Surface of Revolution: Calculus
- Partial Derivatives: Graphical Illustrator
- Plotting Points in 3D: AR Template
- Cylindrical Coordinates: Dynamic Illustrator
- Spherical Coordinates: Dynamic Illustrator
- Circular Paraboloid of Revolution: 3D Augmented Reality Template
- Special Hyperboloid of 1 Sheet as a Locus
- Special Hyperboloid of 2 Sheets as a Locus
- Ellipsoid: Quick Exploration Template
- Special Spheroid Action: Locus Illustration
- 3 Tori Morphing
- Surface of Rev with Helical Cross Section
- Miscellaneous
- Shortest Path Between 2 Points on a Sphere
- 3 Golden Rectangles Surprise!
- Dodecahedral Surprise!
- Holiday Fun!
- Seashell Surface
- Dandelin Sphere Action!
- Modifiable Torus
GeoGebra 3D with AR (iOS): Quick Setup Instructions
WHAT TO DO:
1) Here's the link to GeoGebra 3D Calculator on AppStore. Install it on your iOS device.
2) Once it's installed, open the app. Use the app to create any 3D solid.
Here, we simply created a sphere by using the SPHERE WITH CENTER THROUGH POINT 
tool.
(This tool is the 5th one in on the left on the top row in the pic below).
tool.
(This tool is the 5th one in on the left on the top row in the pic below).
3) Next, press the AR button (lower right within 3D Graphics pane). You'll see everything disappear and you'll see your environment on the screen. Move your device slowly, making sure to AIM IT AT THE FLOOR. Wait a few seconds. Look for a SQUARE to appear. Once you see it, touch anywhere on the screen to place the object in your environment.
Use your fingers to reposition the objects. KEY IS TO MOVE SLOWLY.
Have fun exploring!
4) Press the 3D button (lower right) to exit AR view.
Quick (Silent) Demo (done on iPad)
Quick (Silent) Demo (done on iPhone)
Precalculus
-
1. Exploring Ordered Triples
-
2. Conic Sections: Introduction
-
3. Parabola: Cause and Effect
-
4. Baby-Step Modeling in 3D GC with AR: Part 1
-
5. Baby Step Modeling in 3D GC with AR: Part 2
-
6. Sphere Investigation
-
7. Varignon 3D Action: REVAMPED!
-
8. How to Create a 3D Surface of Revolution by Rotating ANY 2D Figure about ANY LINE
-
9. Spinning a Piecewise Function About xAxis: Quick Demo
Exploring Ordered Triples
TO EXPLORE IN AUGMENTED REALITY:
1) Open up GeoGebra 3D Calculator on your phone or tablet.
If you need help with installing the app on your device, click here for quick setup info.
2) In the app, go to the MENU (upper left).
3) Select SEARCH or OPEN. In the text field that appears, type yxhvm5jx.
Note this is the last string of characters in this URL
You could also try typing the title of this resource here if you want.
4) Select the icon that appears entitled Exploring Ordered Triples.
5) To show the x-coordinate, slide the showxc slider over to 1.
To show the x-coordinate, slide the showyc slider over to 1.
To show the x-coordinate, slide the showzc slider over to 1.
6) You can drag the point WITHIN AUGMENTED REALITY. (See quick screencast below).
You can move the LARGE POINT anywhere you'd like. Explore! What do you notice?
Quick (Silent) Demo
Calculus
-
1. Surface of Revolution: 3D Augmented Reality Template
-
2. Disc Method: REVAMPED!
-
3. Disc Action!!!
-
4. Washer Method: REVAMPED!
-
5. Cylindrical Shells: REVAMPED!
-
6. Calculus: Surface of Revolution formed by Rotating Area Between 2 Functions
-
7. Modifiable Solid: Isosceles Right Triangle Cross Sections Parallel to yAxis (VA)
-
8. Modifiable Solid: Isosceles Right Triangle Cross Sections Parallel to yAxis (VB)
-
9. Modifiable Solid: Equilateral Triangle Cross Sections Parallel to yAxis
-
10. Toblerone Warm Up Modeling Question for Algebra, Geometry, AND Calculus!
-
11. Modifiable Solid: Isosceles Triangle (Modifiable) Cross Sections Parallel to yAxis
-
12. Modifiable Solid: Square Cross Sections Parallel to yAxis
-
13. Custom Solid: Changeable Rhombus Cross Section Parallel to yAxis
-
14. Modifiable Solid: Regular Pentagon Cross Sections Parallel to yAxis
-
15. Modifiable Solid: Regular Hexagon Cross Sections Parallel to yAxis
-
16. Modifiable Solid: Regular Heptagon Cross Sections Parallel to yAxis
-
17. Modifiable Solid: Regular Octagonal Cross Sections Parallel to yAxis
-
18. Modifiable Solid: Regular Nonagon Cross Sections Parallel to yAxis
-
19. Modifiable Solid: Regular Decagon Cross Sections Parallel to yAxis
-
20. Modifiable Solid: Semicircular Cross Sections Parallel to yAxis
-
21. Custom Solid: Elliptical Cross Sections Parallel to yAxis
-
22. Solids with Various Cross Sections: AR Templates
-
23. Arc Length to Surface of Revolution: Calculus
-
24. Partial Derivatives: Graphical Illustrator
-
25. Plotting Points in 3D: AR Template
-
26. Cylindrical Coordinates: Dynamic Illustrator
-
27. Spherical Coordinates: Dynamic Illustrator
-
28. Circular Paraboloid of Revolution: 3D Augmented Reality Template
-
29. Special Hyperboloid of 1 Sheet as a Locus
-
30. Special Hyperboloid of 2 Sheets as a Locus
-
31. Ellipsoid: Quick Exploration Template
-
32. Special Spheroid Action: Locus Illustration
-
33. 3 Tori Morphing
-
34. Surface of Rev with Helical Cross Section
Surface of Revolution: 3D Augmented Reality Template
Here, you can use this template to create a function (f), and rotate it about the xAxis (by using the n slider). The Filling slider adjusts the opacity of this surface.
Note the surface of revolution formed.
You can change the phrase "xAxis" to "yAxis" to rotate the graph of function f about the yAxis instead.
TO EXPLORE IN AUGMENTED REALITY:
1) To explore in Augmented Reality, open up GeoGebra 3D app on your device.
2) Go to the MENU (horizontal bars) in the upper left corner. Select OPEN.
In the Search GeoGebra Resources input box, type qgcz82ae
(Note this is the resource ID = last 8 digits of the URL for this resource.)
3) Position what you see accordingly on your device. Press the AR button in the lower right corner.
Follow the directions that appear.
Shortest Path Between 2 Points on a Sphere
In the context of a SPHERE,
A GREAT CIRCLE is defined to be a CIRCLE that lies on the SURFACE OF THE SPHERE and LIES ON A PLANE that PASSES THROUGH THE CIRCLE's CENTER. In essence, the center of a GREAT CIRCLE and the center of the sphere are the same.
Consequently, a GREAT CIRCLE also the largest possible circle one can draw on a sphere.
In the applet below, the pink arc and blue arc make up a GREAT CIRCLE.
To explore this resource in Augmented Reality, see the directions below the applet.
1.
Note that the black arc and yellow arc (put together) DO NOT make a great circle. Why is this?
Font sizeFont size
Very smallSmallNormalBigVery big
Bold [ctrl+b]
Italic [ctrl+i]
Underline [ctrl+u]
Strike
Superscript
Subscript
Font colorAuto
Justify
Align left
Align right
Align center
• Unordered list
1. Ordered list
Link [ctrl+shift+2]
Quote [ctrl+shift+3]
[code]Code [ctrl+shift+4]
Insert table
Remove Format
Insert image [ctrl+shift+1]
Insert icons of GeoGebra tools
[bbcode]
Text tools
Insert Math
See below this applet for directions.
Directions:
Move the 2 WHITE POINTS anywhere you'd like on the sphere. The PINK ARC is part of a GREAT CIRCLE of this SPHERE. You can move the YELLOW POINT anywhere you'd like as well.
Again, note that the YELLOW ARC is NOT PART of a great circle.
Slide the slider slowly and carefully observe what happens.
2.
How would you describe the SHORTEST DISTANCE between 2 POINTS along a SPHERE? Explain.
Font sizeFont size
Very smallSmallNormalBigVery big
Bold [ctrl+b]
Italic [ctrl+i]
Underline [ctrl+u]
Strike
Superscript
Subscript
Font colorAuto
Justify
Align left
Align right
Align center
• Unordered list
1. Ordered list
Link [ctrl+shift+2]
Quote [ctrl+shift+3]
[code]Code [ctrl+shift+4]
Insert table
Remove Format
Insert image [ctrl+shift+1]
Insert icons of GeoGebra tools
[bbcode]
Text tools
Insert Math
TO EXPLORE IN AUGMENTED REALITY:
1) Open GeoGebra 3D app on your device.
2) Press the 3 horizontal bars (upper left corner). Select OPEN.
3) In the SEARCH TAB that appears, type Gh58sVPx
Note this string of characters can be found in the URL here.
Be sure to either copy & paste this code or type it just the way you see it here.
4) The slider named j controls the entire animation.
Slider k_1 adjusts the opacity (shading) of the green sphere.
Slider a adjusts the radius of the sphere.
Saving…
All changes saved
Error
A timeout occurred. Trying to re-save …
Sorry, but the server is not responding. Please wait a few minutes and then try to save again.