A pavimentação (ou ladrilhamento) é a arte de cobrir um plano com polígonos sem deixar espaços ou sobreposições, de modo que as figuras se encaixem perfeitamente e os ângulos em cada vértice somem 360°. Na arte, algo parecido com a pavimentação é chamada também de Tesselação, que é o processo de cobrir uma superfície com uma ou mais formas geométricas de forma a não deixar lacunas ou sobreposições. Pode também ser conhecida como uma técnica de criar polígonos que se sobreponham.
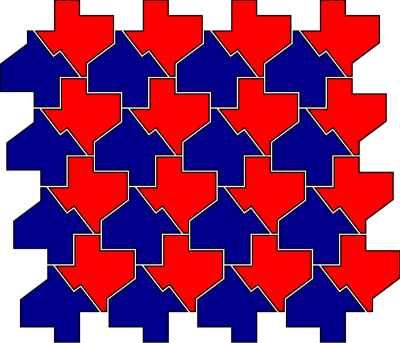
Imagem: Texas tessellation. Link: [url=http://commons.wikimedia.org/wiki/File:Texas_tessellation.svg]http://commons.wikimedia.org/wiki/File:Texas_tessellation.svg[/url]
Para entender isso, pode-se analisar os polígonos convexos regulares – regular significa que todos os lados tem a mesma medida. Abaixo estão cinco deles, ainda há polígonos regulares de oito lados (octógono), nove lados (eneágono), e assim por diante.
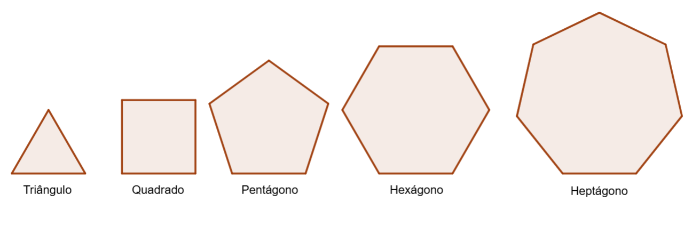
Imagem: Nomenclatura polígonos. Autor
Na técnica de pavimentação, o encontro dos sólidos em um vértice deve completar uma volta perfeita, ou seja, 360°. O triângulo regular (equilátero) tem como ângulo 60°, quadrado 90° e o hexágono 120° - todos esses ângulos dividem 360°. Essa propriedade só vai valer para esses polígonos regulares, os demais têm ângulos que não dividem 360°.[br]
1) Pavimentando o triângulo:[br]
2) Pavimentando o quadrado:[br]
3) Pavimentando o Hexágono:[br]
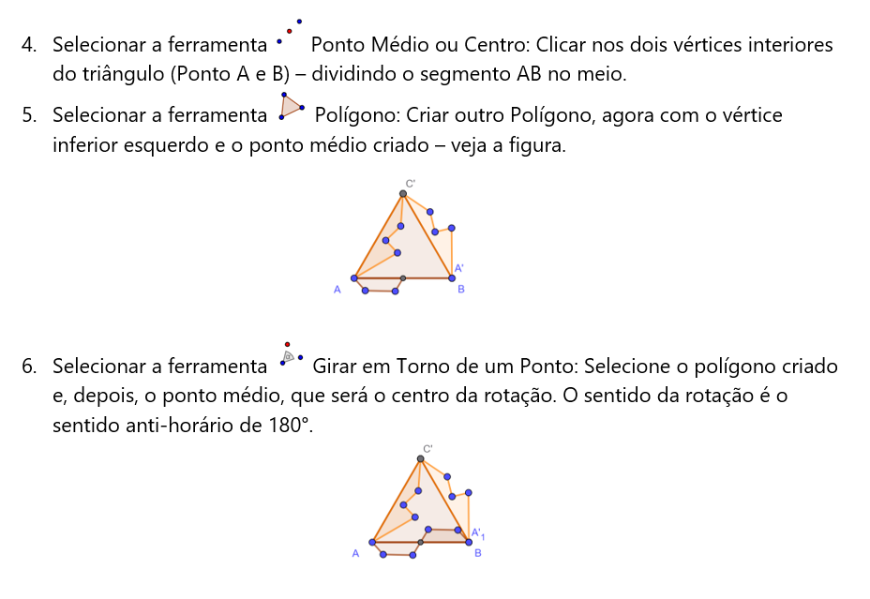
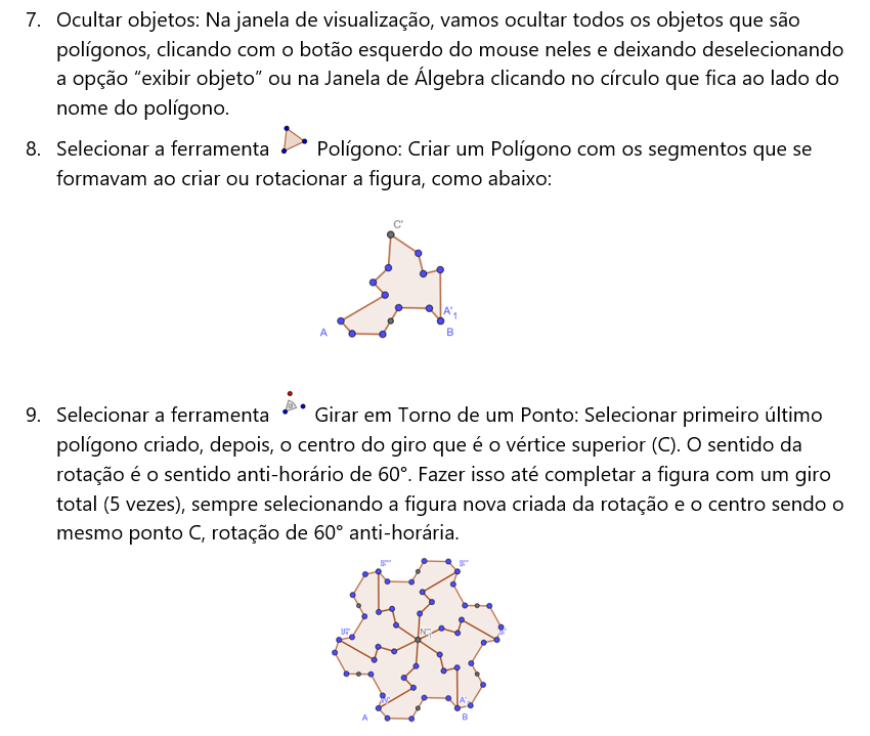
Agora, vamos aprender uma prática de criação de figuras para pavimentação. Essa técnica é a mesma usada pelo artista holandês M. C. Escher.[br]4) Pavimentação por rotação:
Desafie-se: como poderíamos completar a imagem fazendo ela se encaixar nas laterais? Uma dica é utilizar o ponto médio das figuras. Mas, qual seria a transformação isométrica utilizada?
5) Por que as figuras que criamos na atividade 4 se encaixam? Justifique sua resposta.
Resposta: A figura usada inicialmente é um triângulo equilátero e já pode ser usada para pavimentar todo[br]o plano. As transformações usadas nela são isométricas e preservam as medidas da figura. Além disso, também se usa da simetria da própria figura – o ponto médio de um dos seus lados. [br]
É importante entender que há outras combinações de figuras que podem pavimentar o plano. Um exemplo é usar hexágonos regulares e triângulos equiláteros. Outro exemplo está abaixo. [br]

[center]Imagem: Trihexagonal tiling, recolored into star[br]hexagons. Link: [url=https://commons.wikimedia.org/wiki/File:Trihexagonal_tiling_stars.svg]https://commons.wikimedia.org/wiki/File:Trihexagonal_tiling_stars.svg[br][/url][/center]