Q2 II 3. B Vektoraddition und Zahl · Vektor

Herausforderung 1

Berechnen Sie ohne Taschenrechner:[br] [math]\binom{-\frac{2}{3}}{\frac{1}{5}}+\binom{\frac{1}{2}}{\frac{1}{4}}[/math]=

Herausforderung 2:

Berechnen Sie und überprüfen Sie mit dem Applet:[br][math]\begin{matrix}\rightarrow\\u\end{matrix}+\begin{matrix}\rightarrow\\v\end{matrix}[/math] ; [math]\begin{matrix}\rightarrow\\u\end{matrix}-\begin{matrix}\rightarrow\\v\end{matrix}[/math] und [math]\begin{matrix}\rightarrow\\u\end{matrix}+\left(-\begin{matrix}\rightarrow\\v\end{matrix}\right)[/math]

Herausforderung 3

Setzen Sie die Vektoren in die Aussagen ein und überprüfen Sie, ob die Aussagen richtig sind.[math]\begin{matrix}\rightarrow\\u\end{matrix}=\left(\begin{matrix}-1\\-2\\4\end{matrix}\right);\begin{matrix}\rightarrow\\v\end{matrix}=\left(\begin{matrix}2\\3\\-5\end{matrix}\right);\begin{matrix}\rightarrow\\w\end{matrix}=\left(\begin{matrix}0\\2\\3\end{matrix}\right)[/math]; r= 0,5 und s=6[br][br][b][color=#ff7700]Notieren Sie die richtigen Aussagen in das Übersichtsblatt.[/color][/b][br](Laden Sie anschließend eine Aufnahme Ihrer Rechnung hoch.) Fakultativ, wenn die Aufgaben über Groups zur Verfügung gestellt werden[br] [br][br]

[math]\begin{matrix}\rightarrow\\u\end{matrix}+\left(\begin{matrix}\rightarrow\\v\end{matrix}+\begin{matrix}\rightarrow\\w\end{matrix}\right)=\left(\begin{matrix}\rightarrow\\v\end{matrix}+\begin{matrix}\rightarrow\\u\end{matrix}\right)+\begin{matrix}\rightarrow\\w\end{matrix}[/math] [math]r\cdot\begin{matrix}\begin{matrix}\rightarrow\\u\end{matrix}\end{matrix}+r\cdot\begin{matrix}\rightarrow\\v\end{matrix}=r\left(\begin{matrix}\rightarrow\\u\end{matrix}+\begin{matrix}\begin{matrix}\rightarrow\\v\end{matrix}\end{matrix}\right)[/math] [math]\begin{matrix}\begin{matrix}\rightarrow\\u\end{matrix}\end{matrix}+\begin{matrix}\rightarrow\\v\end{matrix}=\begin{matrix}\rightarrow\\v\end{matrix}+\begin{matrix}\rightarrow\\u\end{matrix}[/math] [math]\left(r\cdot s\right)\begin{matrix}\rightarrow\\u\end{matrix}=r\cdot\left(s\cdot\begin{matrix}\rightarrow\\u\end{matrix}\right)[/math] [math]\begin{matrix}\rightarrow\\u\end{matrix}+\begin{matrix}\rightarrow\\v\end{matrix}=-\begin{matrix}\rightarrow\\v\end{matrix}+\begin{matrix}\rightarrow\\u\end{matrix}[/math]

Herausforderung 4:

[math][/math]Lineare Kombinationen von Vektoren: Drücken Sie den Vektor [math]\begin{matrix}\rightarrow\\w\end{matrix}[/math] auf mindestens drei unterschiedliche Weisen durch die restlichen Vektoren aus und geben Sie Ihr Lösung ein (ohne Vektorpfeil).[br][br]Siehe Bild unten

Herausforderung 5:

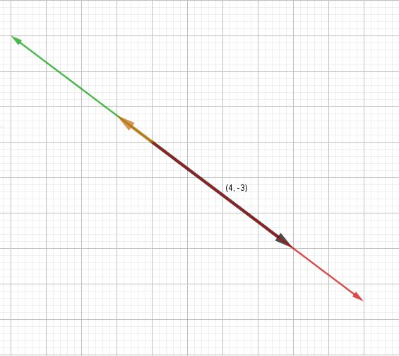
[math]v^{\rightharpoonup}=s\cdot\binom{4}{-3}[/math][br]Bestimmen Sie aus der Abbildung unten die jeweiligen Werte für s und geben Sie diese ein.

Herausforderung 6

Welche der folgenden Formeln zur Berechnung der Mittelspunktskoordinaten sind richtig

[math]\begin{matrix}\rightarrow\\m\end{matrix}=\frac{1}{2}\left(\begin{matrix}\rightarrow\\a\end{matrix}+\begin{matrix}\rightarrow\\b\end{matrix}\right)[/math] [math]\begin{matrix}\rightarrow\\m\end{matrix}=\begin{matrix}\rightarrow\\b\end{matrix}-0,5\cdot\begin{matrix}\rightarrow\\a\end{matrix}[/math] [math]\begin{matrix}\rightarrow\\m\end{matrix}=0,5\cdot\begin{matrix}\rightarrow\\a\end{matrix}+0.5\cdot\begin{matrix}\rightarrow\\b\end{matrix}[/math] [math]\begin{matrix}\rightarrow\\m\end{matrix}=\frac{1}{2}\left(\begin{matrix}\rightarrow\\b\end{matrix}-\begin{matrix}\rightarrow\\a\end{matrix}\right)[/math] [math]\begin{matrix}\rightarrow\\m\end{matrix}=\frac{\begin{matrix}\rightarrow\\a\end{matrix}+\begin{matrix}\rightarrow\\b\end{matrix}}{2}[/math]

Herausforderung 7

Berechnen Sie den Mittelpunkt des Verbindungsvektors zwischen A(-1,3,1) und B ( 3,-5,2) und geben Sie Ihre Ergebnis ein.

Herausforderung 8

Bestimmen Sie die Zahlen r und s, sodass die Gleichung stimmt.[br][math]r\cdot\left(\begin{matrix}3\\-5\\2\end{matrix}\right)+s\cdot\left(\begin{matrix}-1\\-8\\-9\end{matrix}\right)=\left(\begin{matrix}14\\-33\\1\end{matrix}\right)[/math][br]Mit welcher Strategie kann man diese Aufgabe lösen?[br]