de GeoGebra CAS rekenmachine
Welkom bij de [url=https://www.geogebra.org/cas]GeoGebra CAS rekenmachine[/url]! Leer in deze initiatiehandleiding hoe je grafieken van functies kunt tekenen, afgeleiden en integralen kunt berekenen, vergelijkingen oplossen en meer.
Table of Contents
- Eerste stappen
- vergelijking van de GeoGebra apps
- Inleiding
- Verken de app
- Basis
- Uitdrukkingen en variabelen
- Vergelijkingen en ongelijkheden oplossen
- Stelsels van vergelijkingen oplossen
- Functies definiëren
- Limieten van functies
- Afgeleiden bepalen
- Bepaalde en onbepaalde integraal
- Een matrix en zijn inverse matrix
- Geavanceerd
- Rationale functie
- Omwentelingslichaam
- Grafisch onderzoek
- Vierdegraadsfunctie
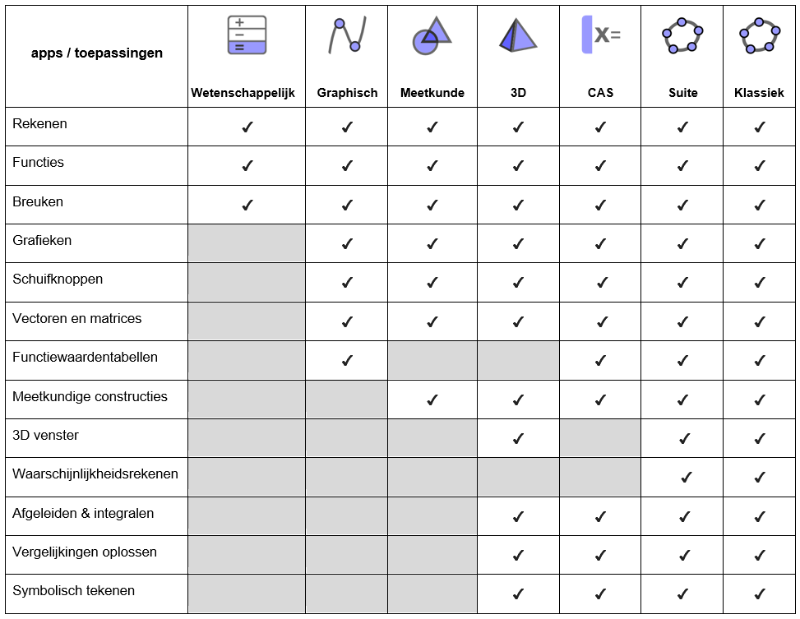
vergelijking van de GeoGebra apps
Met onze GeoGebra wiskunde apps kan je functies, meetkunde, algebra, statistiek en 3D verkennen en leren op een nieuwe en educatieve manier.[br][list][*][url=https://www.geogebra.org/scientific]Wetenschappelijk rekenmachine[/url][br][/*][*][url=https://www.geogebra.org/graphing]Grafisch rekenmachine[/url][br][/*][*][url=https://www.geogebra.org/geometry]Meetkunde[/url][br][/*][*][url=https://www.geogebra.org/calculator]Rekenmachine suite[/url][/*][*][url=https://www.geogebra.org/cas]CAS rekenmachine[/url][br][/*][*][url=https://www.geogebra.org/3d]3D rekenmachine[/url][/*][*][url=https://www.geogebra.org/classic]GeoGebra Klassiek[/url][br][/*][/list]De juiste app voor jou is die app die tegemoet komt aan je noden en, voor gebruik in toetsen of examens, beantwoordt aan de voorschriften van je school of regio. In onderstaande tabel vind je een overzicht van de ingebouwde toepassingen in de verschillende apps.
GeoGebra in toetsen en examens
We geloven dat het goede zaak is dat leerlingen exact dezelfde GeoGebra app kunnen gebruiken in de klas, thuis en tijdens testen en examens. Op deze manier kunnen ze meer oefening opdoen met de app en ze op de beste manier gebruiken in alle situaties. Daarom hebben we onze [url=https://www.geogebra.org/m/y3aufmy8]GeoGebra Examenmodus[/url] gecreëerd en ingebouwd in al onze apps. De examenmodus vergrendelt mobiele toestellen zodat leerlingen niet kunnen communiceren of andere apps gebruiken tijdens een test. Deze benadering werd al uitgetest en goedgekeurd door meerdere ministeries van onderwijs in meerdere regio's. Lees meer over het gebruik van de examenmodus in de initiatiehandleiding [url=https://www.geogebra.org/m/scntsjc9]GeoGebra examenmodus[/url].[br][br]
Uitdrukkingen en variabelen
Opgave
Verken de CAS invoer in het [i]Algebra venster[/i] door uitdrukkingen met variabelen uit te werken en vereenvoudigen.
Verken de constructie...
Stappen
[table][tr][td]1.[/td][td]Typ de uitdrukking [math]a+a[/math] in het [i]Invoerveld[/i] en [i]Enter[/i].[/td][/tr][tr][td][/td][td][b]Opmerking:[/b] GeoGebra toont als resultaat [math]2a[/math]. [/td][/tr][tr][td]2.[/td][td]Typ de uitdrukking [math]4x+3y-2x+y[/math] in het [i]Invoerveld[/i] en [i]Enter[/i][i] [/i]om de uitdrukking te vereenvoudigen.[/td][/tr][tr][td]3.[/td][td]Typ de uitdrukking [math]\frac{\frac{1}{x+y}-\frac{1}{x}}{y}[/math] in het [i]Invoerveld[/i] en [i]Enter[/i][i] [/i]om de uitdrukking te vereenvoudigen.[/td][/tr][tr][td]4.[/td][td]Typ de uitdrukking [math]\left(x+y\right)\left(x-y\right)\left(x-y\right)[/math] in het [i]Invoerveld[/i] en [i]Enter[/i].[/td][/tr][tr][td][/td][td][b]Opmerking:[/b] GeoGebra toont als vereenvoudigd resultaat [math]\left(x+y\right)\left(x-y\right)^2[/math]. [/td][/tr][tr][td]5.[/td][td]Open het menu [i]Meer [/i]rechts van je laatste invoer en selecteer [i]Dupliceren [/i]om hem in de volgende rij nog een keer in te voeren.[/td][/tr][tr][td]6.[/td][td]Gebruik het commando [math]Uitwerken\left(\left(x+y\right)\left(x-y\right)\left(x-y\right)\right)[/math] voor de gekopieerde invoer om de uitdrukking uit te werken.[/td][/tr][/table]
Probeer het zelf...
Rationale functie
Opgave
Gegeven is de functie [math]f\left(x\right)=\frac{x^3+3x^2}{x^2+6x+9}[/math].[br][list=1][*]Plot de grafiek van [i]f(x)[/i].[/*][*]Bepaal de nulwaarden en het domein van [i]f(x)[/i].[/*][*]Bepaal de limieten van [i]f(x)[/i] voor [math]\pm\infty[/math] en de grenswaarden van de functie.[/*][/list]
Verken de constructie...
Stappenplan
[table][tr][td]1.[/td][td]Definieer de functie [i]f(x)[/i] door de invoer [math]f\left(x\right)=\frac{x^3+3x^2}{x^2+6x+9}[/math] in het [i]Invoerveld [/i]te typen en te bevestigen met [i]Enter[/i]. [/td][/tr][tr][td][/td][td][b]Opmerking:[/b] [i]GeoGebra CAS Rekenmachine[/i] vereenvoudigt automatisch de vergelijking van [i]f(x)[/i].[/td][/tr][tr][td]2.[/td][td]Gebruik het commando [math]SnijpuntenxAs(f)[/math] om de nulwaarden te berekenen van [i]f(x)[/i].[br][/td][/tr][tr][td][/td][td][b]Opmerkingen: [/b]Je kunt ook het commando [math]Oplossen(f=0)[/math] gebruiken.[/td][/tr][tr][td]3.[/td][td]Om het domein van f(x) te bepalen, bereken je de nulwaarden van de noemer van f(x) met het commando [math]SnijpuntenxAs(Noemer(f))[/math].[br][/td][/tr][tr][td][/td][td][b]Opmerking:[/b] Je kunt ook het commando [math]Oplossen(Noemer(f)=0)[/math] gebruiken.[/td][/tr][tr][td]4.[/td][td]Omdat de oplossing gelijk is aan [i]-3[/i], vind je als domein [math]D=\mathbb{R}\backslash\left\{-3\right\}[/math].[/td][/tr][/table]
Probeer het zelf...
Stappenplan (vervolg)
[table][tr][td]5.[/td][td]Gebruik het commando [i]Limiet[/i] om de limieten van [i]f(x)[/i] te berekenen. [/td][/tr][tr][td][/td][td]Typ het commando [math]Limiet\left(f,-\infty\right)[/math] om de limiet te berekenen voor [math]x\longrightarrow-\infty[/math].[/td][/tr][tr][td][/td][td]Typ het commando [math]Limiet\left(f,\infty\right)[/math] om de limiet te berekenen voor [math]x\longrightarrow+\infty[/math].[/td][/tr][tr][td]6.[/td][td]Gebruik de commando's [i]Linkerlimiet[/i] en [i]Rechterlimiet[/i] om het gedrag van [i]f(x)[/i] te beschrijven rond [i]-3[/i]. [/td][/tr][tr][td][/td][td]Typ het commando [math]Lnkerlimiet\left(f,-3\right)[/math] in het [i]Invoerveld[/i].[/td][/tr][tr][td][/td][td]Typ het commando [math]Rechterlimiet\left(f,-3\right)[/math] in het [i]Invoerveld[/i].[/td][/tr][tr][td][/td][td][br][/td][/tr][/table]