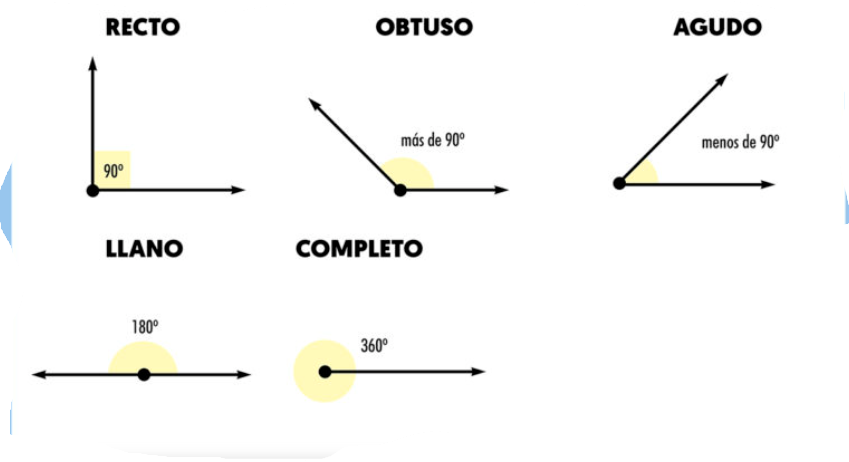
CLASE DE ANGULOS
¿Que es un angulo?
Un ángulo se define como la figura formada por dos líneas con un punto común, llamado vértice. La medida del ángulo se expresa generalmente en grados[br]Existen diferentes tipos de ángulos según su abertura y posición:[br][list][*]Ángulo agudo: Mide menos de 90° y más de 0 °. Los ángulos agudos son más pequeños que un ángulo recto.[/*][/list][list][*]Ángulo recto: Mide 90° y sus lados son siempre perpendiculares entre sí.[/*][/list][list][*]Ángulo obtuso: Mayor que 90° pero menor que 180°. [/*][/list][list][*]Ángulo llano: Mide 180°. Igual que si juntamos dos ángulos rectos. [/*][/list][list][*]Ángulo completo: Un ángulo completo es aquel que mide exactamente 360 grados. Es la vuelta completa alrededor de un punto y se utiliza en geometría circular y trigonometría.[br][/*][/list]

Ángulos complementarios: Dos ángulos son complementarios si su suma es igual a 90 grados. [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAQ4AAAC7CAMAAACjH4DlAAABZVBMVEX///8AAP//xf/09P+U1JTd3f/h4f/r6///AP//x//z9PwAAPrh1//rtP98tp6W15MAkwD/y//v+e8AAAA/P/+lpf/W1v93d/9ycv+03bTT0/+urv+pqf9vb/82Nv/Pz///m/92dv9BQf//0f//9P//b///4P//P///r///5v//d/8AmAAAjQD5/fna2tkAAO4AANcAAIIAAHYpKQAAAIzv7+7/TP//K///vP//Q///1///Xf//7v//uf//qv//hv/X7dd/rqfGlPmSy5TB48GZ3I26urWZmY8pKRgAALcAAGUwMBcAAMkTEwCDg3kAAKAoKCEUFCI8PC+np6JMTDwAAEwAADcAAB4AAEGtrZ4AAFVHR+UAAAUvL///g//rGv/rhf9qAP+ExoQ0qTRiuWKWbvgAYHWw3aVVs1VmRflPYdolpiVnib9OsU55yHkZGQCxg/lgvVxvb2IuN+BVpHgAgSogjkefGhlFAAAHF0lEQVR4nO2di1cTRxSHNxuEDdGaJYCCD6IkhJBEIAJRHhIaBEGFFrC21kcLtGqt9N2/vzN3NhkmySbR09mZ2dzvHJM9nN3Z8TvzmzsDmxPLQhAEQRAEQRAEQRAEQRDC1vb2luo+aMOdR6Wdnd3Hd1T3Qw8Wk08ihCdPF1X3RAv29iPAwp7qnmjBV7NMx+xj1T3Rgq/jno5HqnuiBQfe6Jg7Ut0TLTjcZTpeHKruiR4czVMbJRwcHnvJ3d0k1pU6/XNzA6r7oBH9kQjq4KAOAdQhgDoEUIcA6hBAHQKoQwB1CKAOAdQhgDoEUIcA6hBAHQKoQwB1CKAOAdQhgDoEUIcA6hBAHQKoQwB1CKAOAdQhgDoEUIcA6hAwRcedrUAefjVDx9bTZ6Vvgnga2AgdW8/pM31zSfk+TNCxmGQPfM7dlX4rE3QczrMHHCPfSh8eJujY3vF0lKR/uMIEHd8teDpe4OiwrNHvX3rPiiel30t7HdErkcg8PB0dfyn/g0i667hOPNwc304u7JeSAXwsS28do8PExgg5WDwM5jNqOuuI3iIybkSDvKXGOq4RGcMTwd5TWx31nASKpjpoPYlcDb5neuq4riAngI46Rm+ryAmgnw6Wk0DrCUc7HWzdperumulQU084WulQVU84Oum4pjQngD46xtXVE44uOpTWE44mOtTWE44WOlTXE44GOhTs431RrwP2JxrkBFCtQ4t6wlGrA+rJDdVpPYdSHbrUE45CHaM3iY3rim7ugzIdg1f1qSccVTo02J+0Qo0OHXMCqNAB6y71+5NWKNBB68mr0YBv2iWB6xjXNSdAwDqitJ5cHQzwjp9GsDpG9KwnnCB16J0TIDgdAzQnV7SsJ5zAdNB6clvnnAAB6ZgY1j4nQCA6ojcMyAkQhA5aT4Y1XXc1IF+HAfWEI1sHrLtumZATQLKOESPqCUeqDsjJNWnNS0CiDrbu0uj3wl0gT4dB9YQjS4cp664G5OiImrA/aYUUHabVE44EHYbmBPjfdRixj/elhY5JyjI5SE+nbPqDdGbJ7rY9I+sJp1lH2gEsa8pxVpxs2rKWpnPlqa5ag5wYte5qoFnHlDOZJlhWtkxeyhnLImpS0120Zc4+3pdmHWsOe59y7pFX20lbKynXyXVuakSn51Y+k2Yd6/fdmXWSjUmHBmTZmSQ/yix3bGj8leE5AZp1LDnZ9fvOtJWD0bHmdDWLhiAnQLOOldfkZcZZJV5yxAlI6QSsu8ytJxyfdUfOWbNWy6TAPHDcjm1MGLeP98VHx6pDS8mySybUTiV2kObklr5/Z/wkmnTkQMQkmUFTVETK6dAA/J3xgqzuBU3z6GDLjSz5t0TlpNpeHo56wiE6GuoBmT2zTjlHa6xTdjLtLmb1JCQ5AYiON+VsJmWfmyLsB6y4ptcetF1vwLorNDkBLhIdbJPizKytfsqVIaonHKLjh/WZlSwzstLNIgMYCMm6qwGi45LrujF7en0JjKS6uiyEOQGojphNiMVcO7XUnZBQ5gSo6wAl7r0M8VGOtb1kIHT1hCPoIDAhmbT/FaHZn7SiUQcRMn2fCJn0OZ/mJB7KnADNOkhk1unerdXZIa0nnBY66AAhm9mZ5pNDnROgpQ47Zq84TevziZDtT1rRWgcZIJkGH6HPCeCnA3y85ufRnLwPdU4AXx22O8PnU5qTENcTjr8O2yXzByzIeiMnQBsdtk02dumeyQnQTkfsHim3wvNdxWL9QnZU2VTQZ4m0HR1u6s2P5/cnx/nEhzF2WMkPkdfqyemJqp5Loe3osH+i6676Pv4ssTlULcB4qOSpjmKe/DBU48NfR8z9cpbUk5/f1k4tJqrk9eSUHFUTH5iOIetdb+hwL70nQ+OXd/l8fb6AmYPqqCTGxhI0LJv5D2fq+i4BHx0u5OTmxsPLeRgTHsXKWb5C3oYspoMehYqWOryc/Hr5cl/fu0Senz1WKJyyweLpCButdHg5qT7sI5DhwWeHYrGSZ6WkZ3TEYrWc9AEniY/nL9gsVOhbj+io5aQmo6/vLOH9z4eq9L3CKm1v6BBy4pFPsKXXUIFOqsfMQy/oaMwJ42PilJ17XKhWjgtsHTJWCLsOkpO4mBPGab22jJ3kP3rzauWs6NumwXAdrXICkJ1KRXU3g6Kmo3VOapNHqBbi7WA6WE4iTTmpldq3nRsKB6DDNye1uVSvjcnh4+TdbTlNUx2wPxne8JFB1+mncm7+eRzMz0bi+78tymib6PjdW3f58kdep9/x/LkPX9by5EhG4xeh7b82vmjD3//8239BF/qfe1/l80zGV/mMQ9PxiDHslLyDfRnTx0Ak3gVKBYjs7HoH+4cSdFiD0cHORPVh0PuiJzlhMY899j1gO1KmUgM5Ks3Nzi4cSCm0JrJ1dHAkZeJAEARBEARBEARBEARBEPP5DxUFucvoSHK+AAAAAElFTkSuQmCC[/img][br][br]7. Ángulos suplementarios: Dos ángulos son suplementarios si su suma es igual a 180 grados. [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAR8AAACwCAMAAAABtJrwAAABXFBMVEX/////wP+k26QAAP8vL/8kJP//w/8kHf8bH/On354VJO//xf8AkACp3qn9/f//AP//Kv/Gxv/x8f/39///Of//rf//ZP8AlADLy//u7v+Jif/j4/+vr//Y2P96ev//ev//0f9/f/8+Pv+bm/9NTf/o6P//lv//h///4///3P//jf+7u///Tv//bf//8///Xf8AAN5fX//S0v+oqP/p6eYAALQAAOxGRv9ycv9ZWf//7P//qP86Ov//tv+73rvQ5tB+w35juGPs+OyQ0pCUzZR1wHVNr02v2a+Vlf+QkP8AAJAAAE0AAIXGxr9iYl7s7OmqqqMAAFoAAHDV1dFycmpUVFiQkIUAAMsDAz8nJ0EAAGOXl+RmZv//n/9EgZ2PFvwtpi10k8mLZ/fO6c5risubcvhkgc+wgvlfedJXQVtjS1mheZhZt1lWckIqKjcAADWIt3woKNAHEYM+PkNSkkquAAAGsklEQVR4nO2d/VfaSBSGE66QdYMaTCQIIioiiiB+UuonpIhVi63VurZbd9N1v9vtbnf//3N2ElCsJRM8JcwcuM8PUXJQ37y+cycJmRlBQBAEQRAEQRAEQRAEQRDEGyZWVh4XV1mr4JfoSiS0BnHWMrglGrU206xlcAuxRh3dDrGWwS1R8Esww1oFv0Snh9Xx4gprGdxi158YDLPWwSu2P8kB1jK4ZRoGBiTs3x0ZjcViKWxdCOIZ67Xac9YaOObF6cbG6QvWKril9hIIL89Y6+CV84LlT+GctQ5eeQU2J6x18MrFsmXPdxesdfDK80vSwAqvsQdzYv3Vmzen37NWwTXDACprDVyzBknWErhmWMJbQFQwQHRUANYS+CYJa6wl8A1gBaKCAaIzDBIGiEYSJlhL4BoVJNYS+OYpBogKBsgFDBAdFfysJfDNISyylsA1KuCTClSiGCAqoxggOtMYICoYIBewAtEZxwDRmQZ8GprGOD4OTQcDRGccHrGWwDeTGCAqKQwQnSJEWEvgmhh2YXQwQHRiMMtaAt8UAcfs0kjBY9YS+KaIY56oxDBAdN5igKjEMUB0VjBAVDBALmCA6MThLWsJfPMYYqwlcA0GyAUMEJ1VDBCdWQwQlVUospbANxggOhggF2YhxVoC10RgkrUEvnkE46wlcM1XBWi+D0ZFb7ddgRJj1jYsk01W0ZQdYS6R3fROGCeEoM3ZNdMjlj+5EeLP/MjU1NSmkBfkLU+1ccF2exVIy+WJPyNpLSAIYt7elU73QX7aDdC8EB6ztpY/GU0ZSZB9C0sea+OCGRht631hu/5Y/qQz5GvGU1EcsQjRtt7X9MdCVDwTxBvb7c1e0vQnQ8qOqHkriiMW4bD5YmmB9E1TCy0Kb9OfLCk+2ly35LFnoF6BNsW5vHJLNj228Nm7cjvWNkv696XsiF2f+wUrQJtbYY2Ykkuk5wiZRC5rvbxaaP0TS33Rc93ih7SmaLmrHVGWA3XkwM5Wgpwn52TW4thz/QP8mL8S5YD4GcSlsZymhKdY62NMKagXQLxnTsMiWUwrSqIfWtN1ZZdsjT0CsWS/uV8Pmk/ewU9yK38I8k5O0UR2urtExTyolgXBNKvVklC63is19vt0vTzk8/nBwR7LoS1NSff45CaGTjamIOj2q6Y/+yQ8xJ7Bd/CLU4BIKxNzSri329hBWdgl7cowd0vX5GWpZNi7y0HTR+whSJQAkQgllGxPG1QxzZJeEXaDlQPy5YZysFp3xyVAxKCMku9lgyqkYRlBwyAZ2tONxs79W3sIQA2QKM8p+R6+nTpUJRvTalqkFDX8GSKN65bBn+kBshKUZngAHrNnFWbdKJUb39q7dN9dXAIkyjlljOkxeMqH6i7p3w29sqsf1PeY+pMh3wMCJIpZbZ7tQXjJwb7li1Gx+y/BOmsuD/keFKDAmBJmegjdxNDNe/YM/uoWINLL77DW3S3KeumeP74hgJYXYXfQsqx1d4m9L+JjB+g3eoACmX4J0L7+5L49doBc8hPQ8qyVdwUj+GV82gzQFGvt3cAX3G/hD+nCJJcA7fTySWITU2/ljm/wd7cAyXmtly/DGhh3L7zucuAWIA4a2LD3Y2d3HZqXe4DIOSLrD77WvJ8foxRs0XvdBIh+DhTIsu7Btp96PjKrqreOTxsBksOaV7daYxORNn51HATPnwk0W/XuNwECWaY4FEgo3lykqrPS5Lbk/jDbZFKYvPk8fP3i5Hy981IM3aE82wHa+OPP9xR/5pQOfmJ4dn5y0Vga6JH1IOSh6+xoKsTVSGMu/bPLZSgc1zonp4Ghf3D0x/fXEcDGa2d/rjp4iVE7LcDypZ2AuP0Qibrmdo9yEfySv1GhP9pLd/3dMTk37OnVQSf+ObL+5vL7m8+Z7yOPddCfY/sAP1rfTrQ5p8ystcxA0p4/ZP2Z/eNHnwY6zbfO/GuvFwbHkiMgdUrGJ/t/AS+tFjbR3pQpKbs2p+xxI7f++DvNN474n7n6I3VMxl1/IvXJzUMu7StUL82H9iyXXrUvGmfPurje3GWzfQ3bw6njD+q6z46XYdmD+kzl4qhQ2PivO3+r9sY6wPramhOwGAs9cBkl0r9fdH1lztr5SdeWS7UO8OYEJjTrn8EJ8hEEQSioPf4s1NcRmZGktzio0IkQLKrjUVwv1Yn6pXGxzUFzfUe8fmtlFZe7bE2ovoRRCv1pzWr9MjqO/rRGrc/IkcTJ2xxI+ketUfE4d5sTT2HGjzPUU1BXMTwIgiAIgiAIgiAIgiAIgiAIgiAIgiD88T+l/rhMVUeZ6AAAAABJRU5ErkJggg==[/img][br]8. Ángulos adyacentes: Dos ángulos son adyacentes si comparten un lado y un vértice común, pero no se superponen. Los ángulos adyacentes pueden ser complementarios o suplementarios dependiendo de sus medidas.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAARQAAAC2CAMAAAAvDYIaAAABmFBMVEX///8AAP//nP+Iz4j/AAAAAAD9/f/Pz///AP/1+faK0oZppp3/oP+GAAD19f//n/8AlgCAAADs7P/HmqBtbf+urv+5ubmiTln89ve/v//u7u7b29v37vBUVP9paf9ZWf//kv/z5OewYm/k5ORzAAB7AADmz9OBgYGysv//zs7w8P/t6P+5e4SeOUqWHDTPz89NTU3PpazXtLqeRVHgwcb/1dWbm///5eWHh///sLAaGv8oKP//N/9sOv6PACI7Oztra2sdHR2Rkf/Z2f+MABbGxv+Kioqamprl1db/wcH/oaH/h4f/Wlr/QkJ2dv//fX02Nv//R0dAQP//bW3/kpL/GBjf3///fP//UP/P6M/CcP5bTf+N1n92x3a1cnuTDisqKipubm6lpP//MjL/3P//0f//u///r///6///c///RP9tAP/AAP//ZP9zRv4AbGVeulGdWvwuZLI2TN7fhP11vXV+vZGg06A7rDtdiLlHZc8uPeO33bdtoaiCw4p4sphVfME9WdhEr0RjkbKWVvwvimsAd0hFRUXCgIW9AAAMlUlEQVR4nO2d+UPbyBXHNWApG4IAx4ktsBIsE8sctkGyCMF0HQiEmJCQcIV02TUh5G7Tprs90mu33V7/dt+MjA/wIckzOog/PyAcY2n8zXznvZk3tjiuR48ePXr06NGjR1AZm8VMeN0MfxHlCXcve90QPxHl766vr9/l0143xE9E+WX4GefnvG6InwBRxiYm0vwDrxviJypjSq+j1BPlX6TTx3eJiXpUMMcUjufjHjfET1REWeFnPW6InwD7HB+DfVYEr1viIyoD7UrPPXVcnsCMed2ML4JIvvFx6ZY37fAVkVjjYyWgokzTPNlFEeX+dYonw6LIWiYiw+8SHNVbp79QvIgLCOglvZNhUWJJLbkmcUI+q2VyKRCpGNMyYZ3eRdzgDrpH7VxYFAWOosFpOThq0FOSZfjFSAUrIVpFaIvWuUz7lPMgSl7jzDFFJNZJBcxATxG6SelUIIoilnUlZ3BZbBgQRQqX8DPhgIlyGyG0Q6d3gygaDkDQU5IZOBrQU45wl5FvyVQu4BozIAp6OkTjVCCKLipSOWxwakqXVDzQ6mFDUrJlGqd3k0OsSmGGwplwRpsMi3oOvKMVw1kDROH0o/BahsLJ3eU6Iqx63Q5fMW2Kgu573RBfMW6KskRlXLkojBJN7gUrv2IOa/dIErtzM+Mauj2OCszcI4sl6ucUZqNRtotkq5dwtnKN1enz9KeDs2Q5lXktDwLzKKNTK9TPGOf5dHSd56PUz3yGGwg5NpCsRXQYpxU44EcRTosonBLRYCxR8b/gH5pSimiUBvM50kke8Md0Tteaq84nhqoYy+RUThPLmVxW4tRwLBMTtVwml6us20ayHFeM5TNH+Y7nsoLA83g8EVyIl44NJKzhSZ8kk/WBXATmPfBLLCxx0q2SuUSJlcnhxZYUFStN8DyN01hi3KGB1DVy0LP4p5aFngLHTJIjKwZVUYrYR3TikJuiODWQqQYXSZIHuYooeGJ8VhSBUnDmebw1Lb7sRtXXoYHUMEnODNJhQIwGUTSsWIayKMtkiF12Z9eEwwiUTcqcoXDFjCQY4VKjKKWUIahrMbqijPH8XHrO7C/MueoshZNjR7kcxOA8HAyOK4lcRRS8QJsp5mLYQ/gZoUgpt52Yw/sYXSqFM0zhKDMWd2/H62EXKdyFxaGB3IVepcoi/jfQTGHS9Wt2Mwdyg0m05P5FGRlI2puncRphCyH3OworAz0MhRa6P8vqEkJLnqybOp0DtUXeD+13XSZ8iddNaW4esU4XiwhtWAiFtrs7w9BNUrbzaIGdjYE2QqHdbl6/WiAL7LdptccubCIQDCubzl99u1Kz8yw0MopAT0KhRaevvVfRxPXErQajFO5RKDTl9LWVnkJ156JNGKVwJ10EZjKk3KHZGrtMszGQHArtOywXwn8TJClX6bbHJowMNB8KPXb0wjuQoAztUNue55BDNoVUh4H5OnGO4G1HYbeIAIF5z/aLLiE0zqAt9mG1iOAgMM/Q2pXXPTcY7USwHZiFpwg9Y9ESBzBbhbMbmMf9tPeMlYFsBmZIZil+gKBrmCwicDYD8yTFjfI0YLOIwJHA/Mjin64idINJGxzDbBnb8owZUmt2G88cwspA3Ka1wOynwFOFmYEsBuabfgo8VdjVgawE5nserrS1g1kdyEJgHvVrvZJdIXW+01I2BJ4dNpfuGnYGMmfMUqsq2VABFbxcaGsLu0IqnjHLJ63yuEM/f96G4U4EmDGHWkUhjwqkVmG4E2Ebi9K0q9z2dOXeAswM9DDUqqvcZ5Yg0YKVgTZMTZoEoWfUPgLLDlYGmtpv3lUg8Hi8cG8FVnMgabdpVwG/XmJxObqwmwMtNukqd7zacGETdhFo4fHZrnLd40qgdcBArEa+zcau4pt6RmfYGYiMt7WuMuPVDi4nsNxMCuPtaVcRlhCi8R0DLsF0M+niaVo7HojAU4XRToQKC+aK0x1/1TM648JubL/VMyzAfDf2KkKHTC/AANYfZ5gO5NdQMDaQH+sZFmBWB8L4s57RGZYGuu3TekZn2BnIt/UMC7AykI/rGZ1hNAeaLvivkG6DSSYG2vFzPcMCLAx00/cfXezANH0DBTfwVJmknU8EOfBUoTwHwttkA7Os1BK6iwi4nuHbQroNqKZwvi6k24GigXxeSLcBPQO9DEw9ozO0DHTfd9tku4FOCheoekZnqCwiDAWrntEZGnOggNUzLNC9gYJSSLdB1wYKTiHdBl0aKECFdDt0tRPhaiDrGZ3pahHhogWeKl0YyFcfDKSL4zmQzz4YSJVmcyDp1es3wwnM29ev3jV/XQAL6TY4Y6ChN4kPXzVy8PbVuVcFup5hgbovl3/35uOpEr8gVB8lGnXx4wcDqVJN4d4dmAI8f59I9A0PYvr6EgcfTWk+vKm9RNgJZiHdBqaB3r0ninxMDA4OD/fVAHX6Dp6T596eviLw9QwLgIFm+vDbfp4YrNejTpi+A9xfPrwmf38B6hmdAQP9Ct7yx77BZoqc6nKAB+D30gWpZ3QGJna/ft5OkoosuDe9enbBA0+VQ4T6mhqnUZZhHJyWLkY9ozNgoK87dBTCYOKrwoUPPFVeIvSNJVV+g9BvP3ndWrcAAyUsaPI7hL4fGfnZ69a6hCUDDX6D0A8Dn0ZGvvO6uS5hwUDDv0doqX+gH1T5g9fNdYmOBhpOwCD7x4H+fqzKn7xurjvMdDTQU4SuYE36+z+PjPzS6/a6QwcD4cDz52/7TUZGRi573V53aGsgHHj+cqpJ/3dfzLDSzkA48Px1oL/Kp56BqoGnxueRz1431yVaGwhVAk9/nYH+5nVz3aGVgYYh8Py9QZMvqas0N9Dgv+sCz5fXVXAd6JyBcOD551lNcFfx5xwo0ngfcKP7m5A2MRAJPOc1wV3FjwFIzdW+UgzfJyOW7f6c5wyEA0/hx4HzokAG19/99aij1+4faRwJlO5rfC4CLSH0UzNNIFfxz1Ar47cuKFgEWSCPBVnSjhQZHpPnFfIHssN7rJwx0PDXCP2riXl85p8YvrNkpMgJSVEsqhyXy+TEpLgmZrkyvv1oTBRFhVOLoph0tvekwUA48PyjuSbYP76ZLBsi9ISsRiTQihKXLSrYPhy5H6l0VJY4VVZEnZOyEWcX2KkZCA+yTQJPhZ/9s9okHOlcSZRlUZUkBboKee86HlNAFL1IxpVIFixFbkvqgNoq3CAMsjtNx5NT//hmrpyJ4bevpMJgFNHAnaYmSkWIMn5KdCgKrgMRAw0nILtvGni8EGWs7T3bS6KSUzk5XIk9FVEkUxQzKpMb+zqnEoGGC60Cj8mAmyPtWId7tufL+K1nceamVEQx1kxRSjCYQDwyYKytBKMOSM2+U9aMQG0CT3WkdS/Tf8DzL9o9r6XwMKKuZctZfCdWLIpczJe5MvQPTYwljxTwTzJZNCxcayF0srlxLr8hEQgCz/dtNYFM/0dn77AdQmFrssl3xL3gX/Dt7q8s6WZCousGvB2D2EjRVU5VyS8kp1P1amq3QJBlSWqS3S2Y39O2N9/41CEqwIznh28H2vKZSU6L7wP0dGu0cevlLL8cpXh/5alQHfv7Jycnj7e3H2F2d3ef7Faf2V2sc9IMuRHclQ78579XLtGnciMtEGayVrU+5qOV+9lTYT5kmf3djdNXvUS+YOnaJNlHJuHbtqfbD7XtUJQz/yBj98wDU1MbG4uLiw8fPtzb29x88gR6yu52nSaP9qZqnWXcaz0wMLw8I3l5lF9ZXp7jV5xqsqba+fP5qnnOfivz0GULCNThhJogtWHlLm/i8Fb2ec3Wn8OIs725UR+8hXicmnWdgEVZ2hpt2AQT51ewXg+cDrVnzdOBhTPfmiqk8X/IsoeyCFuj5yLyMb+OD2Ot72Uv6REN/msVLaJDHJUish5R4ZEGcqi4m6iQv2mKGtGcLK/M8Xw6/YJf8bSznGM2OlY5thClVMxnwCO6mMxkszKniLFyUoxkM/mizEVyHEdS/Vw+ljnK27961JRjjk87fgOeQNJ7Scb5vABprCJCelsOq5xU1M2pDxElhudI9teZ5syoF3c8znuDEiZv1RDxTz0HooBtNDIZ0upEAR9JRfuiVFLpMYp5khuoRA1OL+KfxpHQWhR5zYkocXwImiiKuWSgkg4TyTf2FA2PKZkuRPkfH8WHCZ73zfKRJZJZBU/9sjEJPGQ0iqKGdc4o5p2Lss7P1R2Cg1QOpyBrlZOpFAytnJICUUjUycGIGwmnYhl4sIZFcTDQgm+W4/F1x6njxWTWTKejXrfDXwjRdPpBoEbZHj169OjRo0cPv/F/lmiMdi77kHYAAAAASUVORK5CYII=[/img]