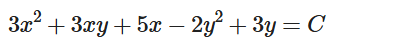
偏微分を積分しよう
[b]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[br][/b][br]前回は、微分方程式の入門としてのかんたんな変数分離を扱いました。[br]今回は、方程式のタイプに応じた解法となる、基本的な視点をふやしてみよう。
全微分df=0。(6x+3y+5)dx+(3x-4y +3)dy=0
全微分df=0。(x^3+3xy^2)dx+(3x^2y+y^3)dy=0
1.完全形と積分因子
[b][size=150]<完全形p(x,y)dx+q(x,y)dy=0>[br][/size][/b]p(x,y)dx+q(x,y)dy=0の型が、[br][b]関数f(x,y)の全微分[/b]を使って、[br][size=150][color=#0000ff][b]df(x,y)[br]=∂f/∂x dx +[/b][/color][b][color=#0000ff]∂f/∂y dy[br]=[/color][color=#0000ff]p(x,y) dx+q(x,y) dy=0[br][/color][/b][/size]と表せる関数fがあるとき完全型という。[br]これは、関数fが連続な偏導関数を持ちfが一定なら全微分df=0となるという意味からきている。[br]完全形の解は陰関数[b]f(x,y)=C[/b](定数)。[b]完全形が[color=#0000ff][size=150]∂p/∂y=∂q/∂x[/size][/color][/b]は同値。[br][color=#0000ff][b]∂f/∂x=p を両辺積分して、f= ∫p dx+c(y) [br][/b][b]∂f/∂y=q を両辺積分して、f= ∫q dy+d(x)[br][/b][/color]これから、∫p[color=#0000ff]dx+c(y) = ∫qdy+d(x)= f となる、fを定める。[br](例)[br][/color]微分方程式[b]dy/dx=-(6x+3y+5)/(3x-4y +3)[br]式変形した([/b]6x+3y+5[b])dx+([/b]3x-4y +3[b])dy=0をf(x,y)の全微分形式とみなす。[br][/b]p=6x+3y+5, q=3x-4y +3とおくと、[size=150]∂p/∂y=∂q/∂x=2だから、完全形。[br][/size]∫(6x+3y+5) dx +c = 3x[sup]2[/sup]+(3y+5)x+c(y) =3x[sup]2[/sup]+5x+3xy+c(y) =f[br]∫(3x-4y +3) dy +d = (3x+3)y-2y[sup]2[/sup]+d(x) = d(x) +3xy-2y[sup]2[/sup] +3y =f[br]この2式を満たす一般解は[b]f(x,y)=3x[/b][sup]2[/sup][b]+5x+3xy-2y[/b][sup]2[/sup][b] +3y=C[br][/b][color=#0000ff]発想は少し高度かもしれないけれど、計算はとても簡単だね。[br][/color][b][br][color=#0000ff](別解)[br][/color][/b]-(6x+3y+5)=3x-4y+3=0の解(x,y) =(-29/33, 1/11)を使って、[br]x=X-29/33, y=Y+1/11とおいて[b]定数項を消して、変数分離型にもちこむ[/b]。[br]dY/dX=dy/dx=-11(6x+3y+5)/11(3x-4y+3)=-(66(X-29/33)+33(Y+1/11)+55)/(33(X-29/33)-44(Y+1/11)+33)[br]=-(66X-58+33Y+3+55)/(33X-29-44Y-4+33)=-(66X+33Y)/(33X-44Y)=-(6X+3Y)/(3X-4Y)[br]u=Y/XとおくとdY/dX=-(6+3(Y/X))/(3-4(Y/X))=(6+3u)/(4u-3)。[br]Y=Xuの両辺微分dY/dX=(Xu)'=u+X・du/dXからu+X・du/dX=(6+3u)/(4u-3)。[br]X/dX={(6+6u-4u[sup]2[/sup])/(4u-3)}/duから(4u-3)/2(3+3u-2u[sup]2[/sup]) du=1/X dXと変数分離。[br] [math]\int\frac{4u-3}{3+3u-2u^2}du=2\int\frac{1}{X}dX[/math] から、 [math]-log\left|3+3u-2u^2\right|=2log\left|X\right|+c[/math] となり、[math]X^2\left(3+3u-2u^2\right)=X^2\left(3+3\frac{Y}{X}-2\left(\frac{Y}{X}\right)^2\right)=3X^2+3XY-2Y^2=C[/math] だから、[br]3(x+29/33)[sup]2[/sup]+3(x+29/33)(y-1/11)-2(y-1/11)[sup]2[/sup]=C (C=0の場合も含む)[br]式を整理すると、[br][b]3x[/b][sup]2[/sup][b]+5x+3xy-2y[/b][sup]2[/sup][b] +3y+D=C(D=Cの場合も含む)[br][/b][color=#0000ff]発想は単純だけで、計算の手間が増えるね。[br][/color][size=150][size=100][color=#0000ff](例)[br][/color]微分方程式[b]dy/dx=-[b](x[sup]3[/sup]+3xy[sup]2[/sup])/[b](3x[sup]2[/sup]y+y[sup]3[/sup])[/b][/b][/b][br][b]式変形した(x[sup]3[/sup]+3xy[sup]2[/sup])dx+(3x[sup]2[/sup]y+y[sup]3[/sup])dy=0をf(x,y)の全微分形式とみなす。[/b][br]p=x[sup]3[/sup]+3xy[sup]2[/sup], q=3x[sup]2[/sup]y+y[sup]3[/sup]とおくと、[size=150]∂p/∂y=∂q/∂x=6xyだから、完全形。[br][/size]∫(x[sup]3[/sup]+3xy[sup]2[/sup]) dx+c= 1/4x[sup]4[/sup]+1/2(3y[sup]2[/sup])x[sup]2[/sup]+c(y) =1/4(x[sup]4[/sup]+6x[sup]2[/sup]y[sup]2[/sup]+4c(y)) =f[br]∫(3x[sup]2[/sup]y+y[sup]3[/sup]) dy+d= 1/2(3x[sup]2[/sup])y2+1/4y[sup]4[/sup]+d(x) =1/4( d(x) +6x[sup]2[/sup]y[sup]2[/sup]+y[sup]4[/sup]) =f[br]この2式を満たす一般解はf(x,y)=1/4(x[sup]4[/sup]+6x[sup]2[/sup]y[sup]2[/sup]+y[sup]4[/sup])=C[br][/size][b][br]<積分因子>[/b][/size][br]Pdx+Qdy=0が完全微分形でなくても、適当な式Mをかけて完全型になるときMを積分因子という。Mの求め方としては次のやり方がうまくいくときがある。[br]N=(Py-Qx)/Qがxだけの関数なら、M(x)=exp(∫Ndx)[br]N=(Qx-Py)/Pがyだけの関数なら、M(y)=exp(∫Ndy)[br]他にP,Qのx、yの指数を見比べるMの指数を考えるなど。[br][color=#0000ff](例)[br][/color]微分方程式dy/dx=-(1-xy)/(xy-x^2)[br][b](1-xy)dx+(xy-x^2)dy=0[/b]に適当なMをかけて完全形にするためのMは?[br]M=1/xとして、p=1/x-y, q=y-xとおくと、∂p/∂y=∂q/∂x=-1だから、完全形になった。[br]∫(p) dx+c=log|x|+c(y) =f(x)[br]∫(q) dy+d= 1/2y[sup]2[/sup]-yx+d(x)= =f(x)[br]この2式を満たす一般解は[b]f(x,y)=log|x|+1/2y[sup]2[/sup]-xy=C[/b]
積分因子でdf=0。(1-xy)dx+(xy-x^2)dy=0
2.実装
[color=#9900ff][u][b][size=150]質問:全微分形式の微分方程式をコードで解くにはどうしたらよいでしょうか。[br][/size][/b][/u][/color][br]sympyは陽関数の形式でのy'=f(x,y)の形で情報を与えると、陽関数の形式で返します。[br]全微分形式では、x、yのどちらが独立変数ということはないのですが、yがxの関数としてかいてみます。[br][b]y = Function('y') [br][/b]dy/dxをDerivative(y(x), x)とかきましょう。[br][br][IN]=======================================[br]from sympy import symbols, Eq, Function, dsolve[br]x, y = symbols('x y')[br]y = Function('y') # y=f(x)[br][br]def dydxEq(fx):[br] deq = Eq(y(x).diff(x), fx)[br] return dsolve(deq, y(x),implicit=True)[br]dydxEq(-(6*x+3*y(x)+5)/(3*x-4*y(x) +3))[br][OUT]=====================================[br][Eq(y(x), 3*x/4 - sqrt(C1 + 35937*x**2 + 63162*x)/132 + 3/4),[br] Eq(y(x), 3*x/4 + sqrt(C1 + 35937*x**2 + 63162*x)/132 + 3/4)][br][br]すごい係数になってしまい、陰関数で返すに指定しても陽関数で返されてしますます。[br][br]そこで、全微分形式で、f(x,y)=∫pdx + c(y)= ∫qdy + d(x)の考え方で、f(x,y)=Cを求めてみましょう。[br]fpdxと∫qsyの共通項はxとyの両方の変数をもつ項です。[br][br]だから、集合で考えると[br][color=#0000ff][b]A=∫pdx=xのある項、[br]B=∫qdy=yのある項、[br]A∩B=xとyの両方ある項[br]だから、解の方程式はA∪B-A∩B=Cです。[br][/b][/color]#[IN]Python===============================[br]#全微分形式 p(x,y) dx + q(x,y) dy=0の解[br][b]from sympy import symbols, Eq, Function, dsolve, integrate[br]import sympy[br][/b][color=#0000ff]def perfectDiff(p_xy,q_xy):[br][/color] # 積分変数を定義[br] x, y ,C= symbols('x y C')[br] #p,qを積分して展開する[br] px = integrate(p_xy, x).expand()[br] qy = integrate(q_xy, y).expand()[br] #多項式を合併する[br] A=set(list(px.args))[br] B=set(list(qy.args))[br] poly=list(A.union(B))[br] return Eq(sum(poly),C)[br]x, y ,C= symbols('x y C')[br][b][color=#0000ff]p = 6*x+3*y+5[br]q = 3*x-4*y+3[br]perfectDiff(p,q)[br][/color][/b]#[OUT]==================================
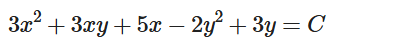
#[IN]========================[br][b][color=#0000ff]p=x**3+3*x*y**2[br]q=3*x**2*y+y**3[br]perfectDiff(p,q)[br][/color][/b]#[OUT]======================[br]
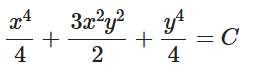
#====================[br][color=#0000ff][b]p=1/x-y[br]q=y-x[br]perfectDiff(p,q)[br][/b][/color]#=====================
[b][size=150]<勾配(grad)>[br][/size][/b]惑星Jの東経x、北緯yの地点の山の高さをf(x,y)としましょう。[br]xを固定したときの山の断面でのy方向の勾配が∂/f∂x[br]yを固定したときの山の断面でのx方向の勾配が∂f/∂yです。[br]山の斜面での最大傾斜線の傾きが[color=#0000ff][b]全微分df[/b][/color]です。[br][b][color=#0000ff][size=150]df = ∂/f∂x dx+ ∂f/∂y dy[br][/size][/color][/b]x,y地点での微小ベクトルdr=(dx, dy)にたいして、[br] (∂/f∂x, ∂f/∂y)を[color=#0000ff][b][size=150]勾配grad f演算[/size][/b][/color]といいます。[br]df = grad f drとベクトルの内積の結果[br][br][color=#9900ff][u][b][size=150]質問:fをz方向として、geogebraで3Dで山と各点でのdf=0の確認をするにはどうしたらよいでしょうか。[br][/size][/b][/u][/color][br]たとえば、冒頭の全微分の場合は、先に曲面の方程式を与えましょう[br]f(x,y)=3x[sup]2[/sup]+5x+3xy-2y[sup]2[/sup] +3y[br]これが山fです。[br][b][color=#0000ff]Derivative(f, x)[/color][/b]とすると、[br]∂/f∂x=6x+3y+5が計算されます。これをp(x,y)とします。[br]Derivative(f, y)とすると、[br]∂f/∂y=3x-4y +3が計算されます。これをq(x,y)とします。[br]山を水平に切るために、スライダーcを作ります。[br]z=cの数式だけで、高さcの水平面rができます。[br][color=#0000ff][b]IntersectionPaths(f,r)[/b][/color]を使うと、交線eq1が図でかけます。[br]これって、山の等高線になっているね。[br][br]f(x,y)=cと同等な数式を入れると、山を切る交線としての曲線eq2ができますね。[br]これは、z座標が表面に出てこないので、xy平面(グラフィックビュー)の曲線になる。[br]曲線eq2にあるA点でベクトル[b]dr=(dx,dy)[/b]を作り、それを動かすためのx座標をスライダーaxで作ります。[br][b][color=#0000ff]Solution(f(ax, y)=c,y)[/color][/b]とすると、Aのy座標のリストysが得られます。[br]1つの交点で十分なので、ay=ys(1)とすると、1つめの交点のy座標を求めてくれます。[br]そこで、[b]Aを(ax,ay)[/b]で定義しましょう。[br][br][b]m(x,y)=-p(x,y)/q(x,y)とおき、C=(ax+1, ay+m(ax,ay))とすることで、[br]dr=Vector(A,C)で接線の方向ベクトルとしての[color=#0000ff]増分ベクトルdr[/color]ができるね。[br][/b]どうようにして、[b][color=#0000ff]勾配ベクトルgrad f[/color][/b]をつくります。[br][b]D=(ax+p(ax,ay), ay+q(ax,ay))[/b]として、[b]gradf=Vector(A,D)[/b]とします。[br]内積[color=#0000ff][b]gradf *dr=0[/b][/color]なら、[br][b][color=#0000ff][size=150]df = ∂/f∂x dx+ ∂f/∂y dy=0[/size][/color][/b][br]となります。[br]グラフィックビューで[color=#0000ff][b]2つのベクトルが直交する[/b][/color]のが確認できますね。[br]また、gradf ベクトルが相当でかいので、[b][color=#0000ff]山というより断崖絶壁[/color][/b]のような勾配になっているのことも[br]感じられるでしょう。[br][br]このように、f(x,y)を基点にして、数式を連携させると、[br]f(x,y)の式を変えるだけで、すべてが連動して変わりますね。[br][br]