Augmented Reality (3D GC): Explorations & Lesson Ideas
This book contains an introduction, lesson ideas, and various means through which math teachers can use GeoGebra Augmented Reality to create dynamic, student-centered, exploratory learning environments. This volume will continue to grow over time.
Table of Contents
- Getting Started (Intro)
- GeoGebra 3D with AR (Android): Quick Setup Instructions
- Quick Tutorial: How to Use GGB AR on Devices with ARCore by Google Installed on Them
- How to Explore Any Public GeoGebra Resource in Augmented Reality
- Geometry Explorations
- Surface Area: Intuitive Introduction
- Volume: Intuitive Introduction
- Rotating 2D Graphs about Lines to Create 3D Surfaces of Revolution in GeoGebra AR
- Surface of Revolution: GeoGebra Augmented Reality Template
- Rectangular Prism Diagonal Exploration in GeoGebra AR
- Exploring Modifiable Triangular Prisms in GeoGebra AR
- Unwrapping a Cylinder: REVAMPED!
- Cone Anatomy
- The 5 Platonic Solids
- Cube: Exploration Template
- Tetrahedron: Exploration Template
- Octahedron: Exploration Template
- Dodecahedron: Exploration Template
- Icosahedron: Exploration Template
- Precalculus Explorations
- Conic Sections: Introduction
- Calculus Explorations
- Disc Method: REVAMPED!
- Disc Action!!!
- Rotating Function Graphs about the xAxis within GeoGebra AR
- Surface of Revolution: GeoGebra Augmented Reality Template
- Washer Method: REVAMPED!
- Cylindrical Shells: REVAMPED!
- Custom Surface of REV in GeoGebra AR: Template
- Solids with Various Cross Sections: AR Templates
- Arc Length to Surface of Revolution: Calculus
- Partial Derivatives: Graphical Illustrator
- Spherical Coordinates: Dynamic Illustrator
- Cylindrical Coordinates: Dynamic Illustrator
- Circular Paraboloid of Revolution
- Special Hyperboloid of 1 Sheet as a Locus
- Special Hyperboloid of 2 Sheets as a Locus
- Miscellaneous Explorations
- 3 Golden Rectangles Surprise!
- Dodecahedral Surprise!
- Holiday Fun!
- Seashell Surface
- 3D Modeling Challenges
- 3D AR Modeling Challenge 1
- Modeling Demos
- Circular Helix (with Slinky) Modeling Exploration within GeoGebra AR
- Modeling a Light Fixture within GeoGebra AR
GeoGebra 3D with AR (Android): Quick Setup Instructions
WHAT TO DO:
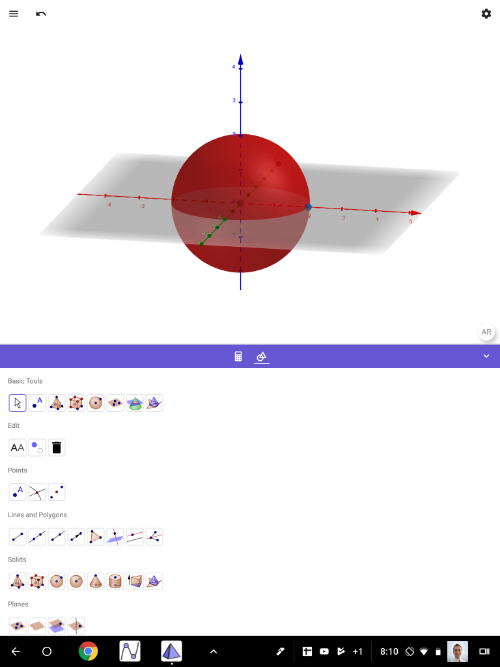
First, make sure your Android device is on [url=https://developers.google.com/ar/discover/supported-devices]this list[/url]. If it isn't, you'll either have to use another device or perhaps update the operating system on your current device. [br][br][b]Here's what to do: [/b] [br][br]1) Install [b][color=#9900ff]Google Play Services for AR[/color][/b] on your device. [url=https://play.google.com/store/apps/details?id=com.google.ar.core] It can be found on Play Store HERE[/url]. [br][br]2) Install [url=https://play.google.com/store/apps/details?id=org.geogebra.android.g3d]GeoGebra 3D Calculator[/url] on your device. [br][br]3) Open up GeoGebra 3D Calculator app. Create any 3D solid. [br] Here, we simply created a sphere by using the SPHERE WITH CENTER THROUGH POINT [icon]/images/ggb/toolbar/mode_sphere2.png[/icon] tool. [br] (This tool is the 5th one in on the left on the top row in the pic below).
4) Next, press the [b]AR [/b]button (lower right within 3D Graphics pane). You'll see everything disappear and you'll see your environment on the screen. Move your device slowly, making sure to AIM IT AT THE FLOOR. Wait a few seconds. If you don't see triangles starting to appear (see pic below), try slowly moving closer to the floor. Hold your device steady. Key is to MOVE SLOWLY until you see a bright yellow triangulated-floor appear over the flat surface onto which you're projecting. You may also see a SQUARE (see pic). Once you do, touch anywhere on the screen. [br][br]This will virtually "place" the object(s) you were viewing within your environment. Use your fingers to reposition the objects. KEY IS TO MOVE SLOWLY. [br][color=#9900ff][b][br]Have fun exploring! [/b][/color]
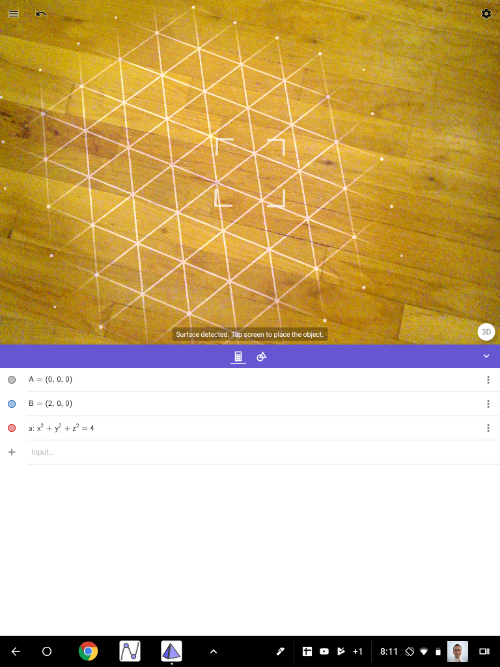
5). Press (ideally) in the SQUARE or somewhere on the triangulated floor. You should then see the image (sphere) appear. Use your fingers to bring the object closer: Zoom in, zoom out, GO INSIDE! (Just move slowly.) [br][br][b]Enjoy!!![/b][br]
Here's a quick 3D modeling demo.
Surface Area: Intuitive Introduction
TEACHERS:
For an introductory class activity related to this, [url=https://www.geogebra.org/m/mgwejudc]click here[/url].
Cube: Exploration Template
Slide the CreateNet slider slowly.
Conic Sections: Introduction
Explore with this app for a bit. Then use it to help answer the thinking questions that follow.
1.
[color=#bf9000][b]Note the equation of the plane is z = some constant. [/b][/color][color=#bf9000][b]Change the equation of this yellow plane to z = 2. [br]Then change it to z = 1. [br]Then change it to z = 4. [/b] [/color][br][br]How would you describe the intersection of this [b][color=#bf9000]plane[/color] [/b]and [color=#1e84cc][b]double-napped cone[/b][/color]?
2.
Change the [color=#bf9000][b]equation of the plane[/b] [/color]to [math]z=x+2[/math] . How would you describe the intersection of this [color=#bf9000][b]plane[/b][/color] and [color=#1e84cc][b]double-napped cone[/b][/color] now?
3.
Change the [color=#bf9000][b]equation of the plane[/b] [/color]to [math]z=0.5x+2[/math] . How would you describe the intersection of this [color=#bf9000][b]plane[/b][/color] and [color=#1e84cc][b]double-napped cone[/b][/color] now?
4.
Change the [color=#bf9000][b]equation of the plane[/b] [/color]to [math]z=4x+2[/math] . How would you describe the intersection of this [color=#bf9000][b]plane[/b][/color] and [color=#1e84cc][b]double-napped cone[/b][/color] now?
Disc Method: REVAMPED!
CALCULUS STUDENTS:
This resource can be used to illustrate how a solid of revolution is formed by rotating the area bound by the yAxis, a function [i]f[/i], and the vertical lines [i]x = a[/i] & [i]x = b[/i]. [br][br]When a differential rectangle is spun around the xAxis, it creates a surface of revolution called a [i]disc[/i]. [br][b][br]You can alter the following parameters:[/b][br][br]function [i]f[br][/i]lower limit of integration ([i]a[/i])[br]upper limit of integration ([i]b[/i])[br]n = number of differential rectangles. [br][br]The width of each rectangle = [math]\Delta x=\frac{b-a}{n}[/math][br][br][b][color=#1e84cc]To explore this resource in Augmented Reality, see the directions below the first screencast. [/color][/b]
Given that the width of each differential rectangle = [math]\Delta x[/math] and the height of each rectangle = [math]f\left(x\right)[/math], write an expression for the volume of one disc.
To Explore in Augmented Reality:
1) Open up GeoGebra 3D app on your device. [br] [br]2) Go to the menu (upper left). Select OPEN. Under SEARCH, type [b]s7mqyzee[br][br][/b]3) The [math]\alpha[/math] slider controls the angle. [br] [b]a [/b]and [b]b [/b]control the upper and lower limits of integration. [br] The colored filling sliders are also there. [br] To change the function (even though it's labeled "[b]f[/b]"), change function [b]h[/b]. [br] [b]n = number of discs[/b].
3 Golden Rectangles Surprise!
Creation of this applet was inspired by a [url=https://twitter.com/pickover/status/902195365407059969]tweet[/url] from [url=https://twitter.com/pickover]Cliff Pickover[/url]. [br][br]Slide the slider [b]very slowly[/b]. [br][br][b]Enjoy! [br][br][color=#1e84cc]To explore in Augmented Reality[/color][color=#1e84cc], see the directions below the applet. [/color][/b]
TO EXPLORE IN AUGMENTED REALITY:
1) Open up GeoGebra 3D app on your device.[br][br]2) Go to MENU (upper left corner). [br] Go to OPEN. Under [b]Search[/b], type [b]YGu6kVpR[/b]. [br] Find the slider named [b]b[/b] and slide it slowly.
3D AR Modeling Challenge 1
STUDENTS:
The goal of this first modeling challenge is to build this trash can (shown in this screencast below) using the tools of GeoGebra's 3D Graphing Calculator. If your device has [b][color=#9900ff]ARCore by Google[/color][/b] installed on it, you can then explore this model within GeoGebra Augmented Reality! [br][br][b]Question to consider: [/b][br]What 2 solids compose this trash can model? [b][br][br]Modeling Clues:[br][/b]For this particular trash can, the height of the [b][color=#1e84cc]blue surface[/color][/b] is three times the radius of the [b][color=#a64d79]red/pink surface[/color][/b].
Quick Demo
Circular Helix (with Slinky) Modeling Exploration within GeoGebra AR
Modeled below within GeoGebra Augmented Reality is a [b]CIRCULAR HELIX. [/b]Parametric equations for this curve are given as follows: [br][br][math]x=a\cdot\cos\left(t\right)[/math][br][math]y=a\cdot\sin\left(t\right)[/math][br][math]z=k\cdot t[/math]. [br][br][i]a[/i] = the radius of the circle seen here. [br]In this demo, [i]a[/i] = 12. Also, [i]k[/i] = 1 and [i]t[/i] ranges from [math]-6\pi[/math] to [math]6\pi[/math]. [br][br]Other than a slinky, what other every-day real-world objects can be modeled with a circular helix?