
9.Sınıf Eşitsizlikler
Doğru Grafiği Verildiğinde Doğrunun Denklemini Oluşturma
Bir doğrunun grafiği verildiğinde, doğrunun denkleminin nasıl bulunacağını hatırlayınız.
[i]Bir doğrunun denklemi, eğim (eğim katsayısı) – y-kesişimi formu kullanılarak y = m x + c Bu noktada, daha önce öğrendiğiniz bilgileri hatırlamanız beklenmektedir.[br][br][b]2x + y = 2, [br]y – x = 0,[br]y+ x = 0 denklemlerinin grafikleri öğrencilerle beraber çizilir. [/b][/i][b][br][br]Bir denklem, analitik düzlemi kaç bölgeye ayırır? Bu iki bölge neyi temsil etmektedir? [br][/b]
Sürgü yardımıyla katsayıları değiştirerek, parametrik değişimlerin eşitsizlik sisteminin çözüm kümesi üzerindeki geometrik yansımasını dinamik olarak analiz ediniz."

SORU:
[b]İlgili geogebra etkinliğinde y>x+1 ve y≤-x eşitsizlik sisteminin çözüm kümesini analitik [br]düzlemde gösteriniz.[/b]

Soru-1.a
[b]Eşitsizlik sistemini, grafik yardımıyla bulunuz.[/b]
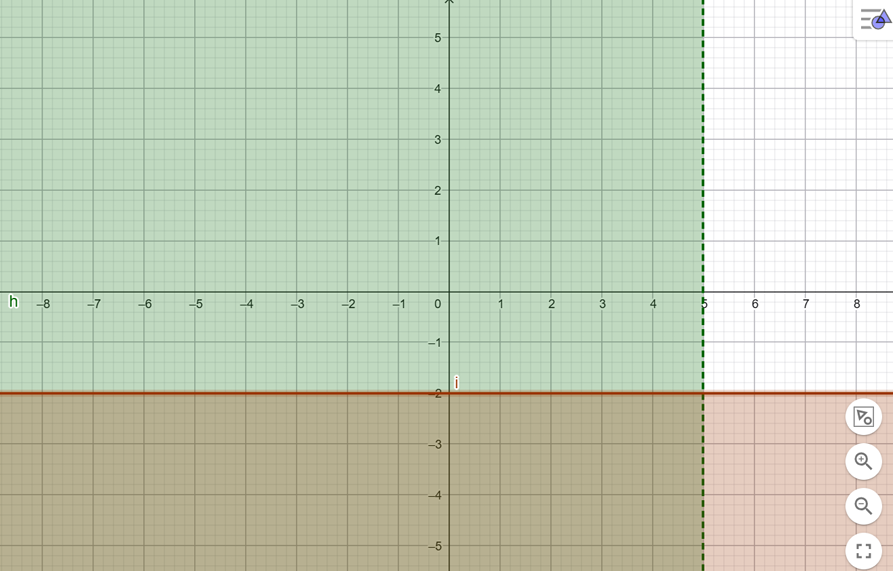
Soru-1.b
[b]Eşitsizlik sistemini, grafik yardımıyla bulunuz.[/b]
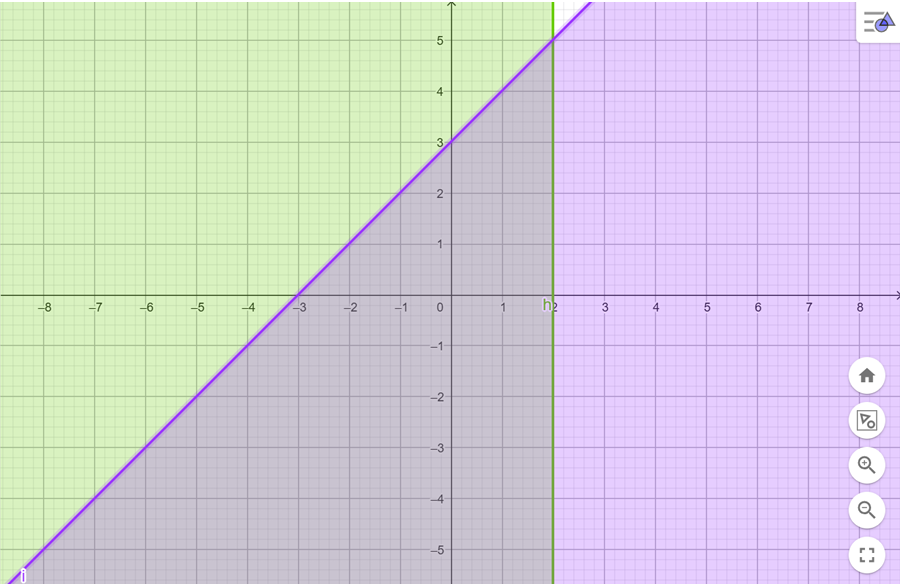
Soru-1.c
[b]Eşitsizlik sistemini yazınız.[/b]
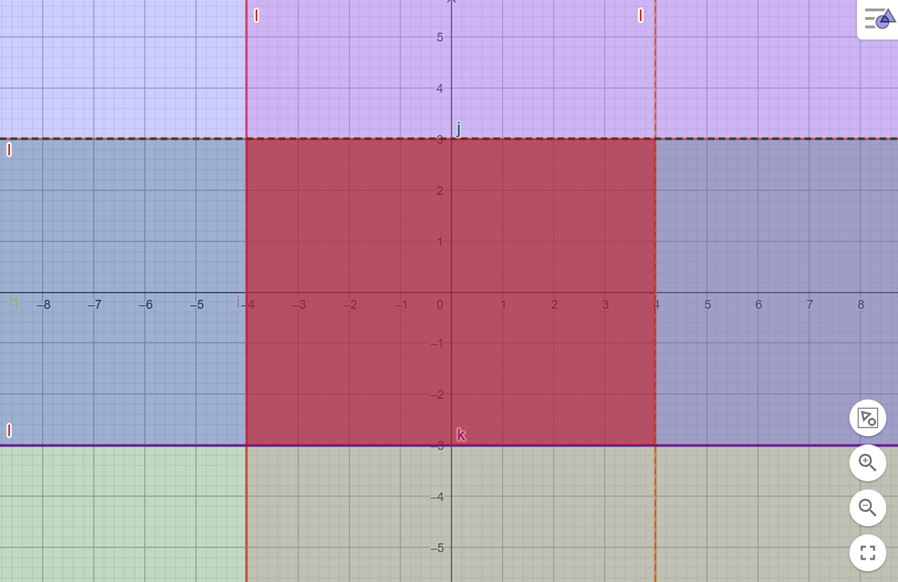
Soru-1.d
[b]Taralı kırmızı alanı veren eşitsizliği yazınız. Eşitsizlik sisteminin çözüm [br]kümesini bulunuz. [/b]
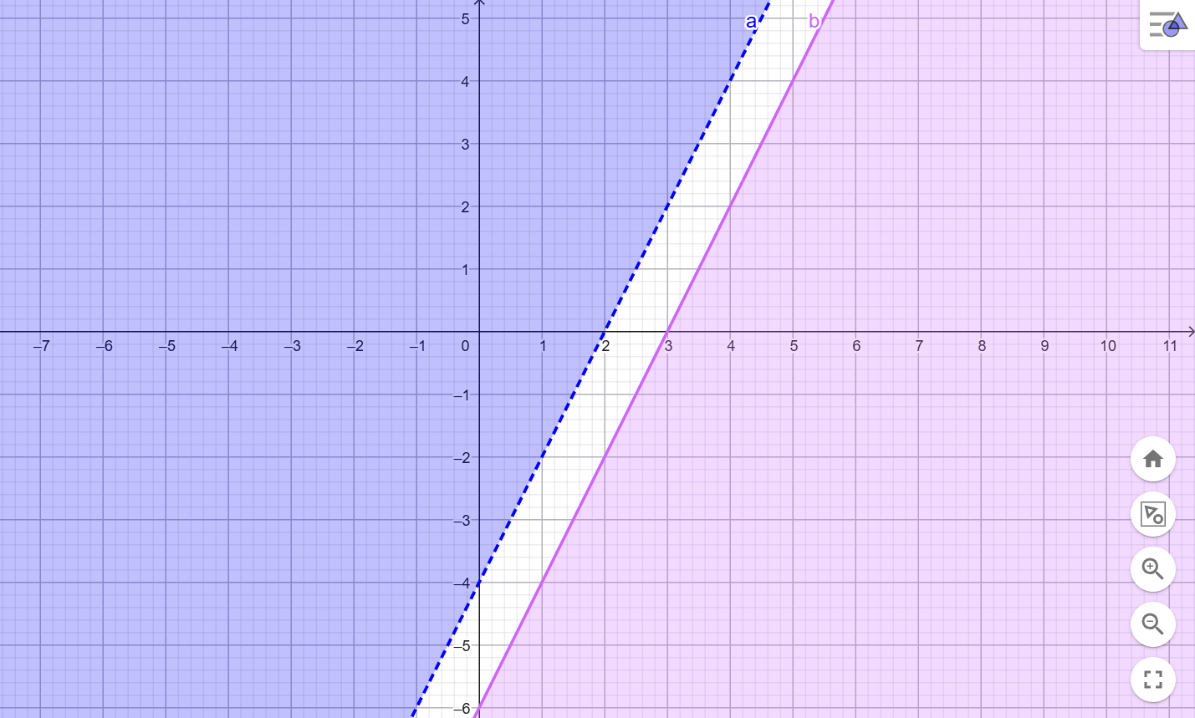
Soru-1.e
[b]Taralı alanı veren eşitsizliği yazınız. Eşitsizlik sisteminin çözüm kümesini [br]bulunuz.[/b]
"Sistem tarafından rastgele atanan doğrusal kısıtlar altında oluşan kapalı bölgelerin analitik karşılıklarını (eşitsizlik sistemlerini) saptayınız."
Soru-2
[b][i]Bir kaşif, koordinat düzlemiyle modellenmiş gizemli bir adada, kırmızı ile taralı "Yasak [br]Bölge"nin içinde kalan antik bir elması bulmaya çalışıyor.[/i][/b]
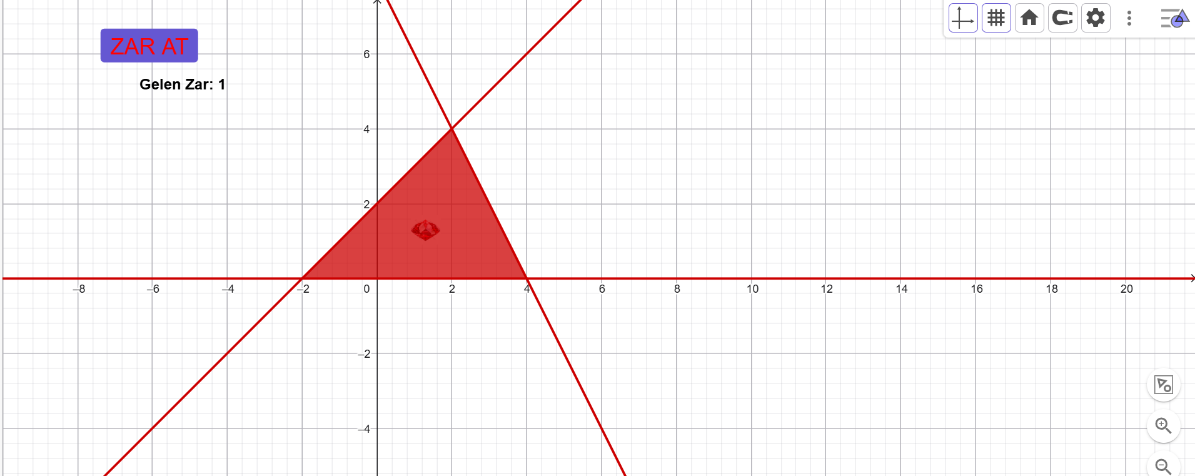
[b]a) Elmasın bu bölge içinde kalabilmesi için apsisinin (x) alabileceği tam sayı [br]değerleri toplamı kaçtır? [br][/b][br][b]b)“Yukarıda verilen grafikte taralı bölgeyi tanımlayan doğrusal eşitsizlik sistemini [br]yazınız ve her bir eşitsizliğin grafikteki hangi sınıra karşılık geldiğini açıklayınız.”[/b]
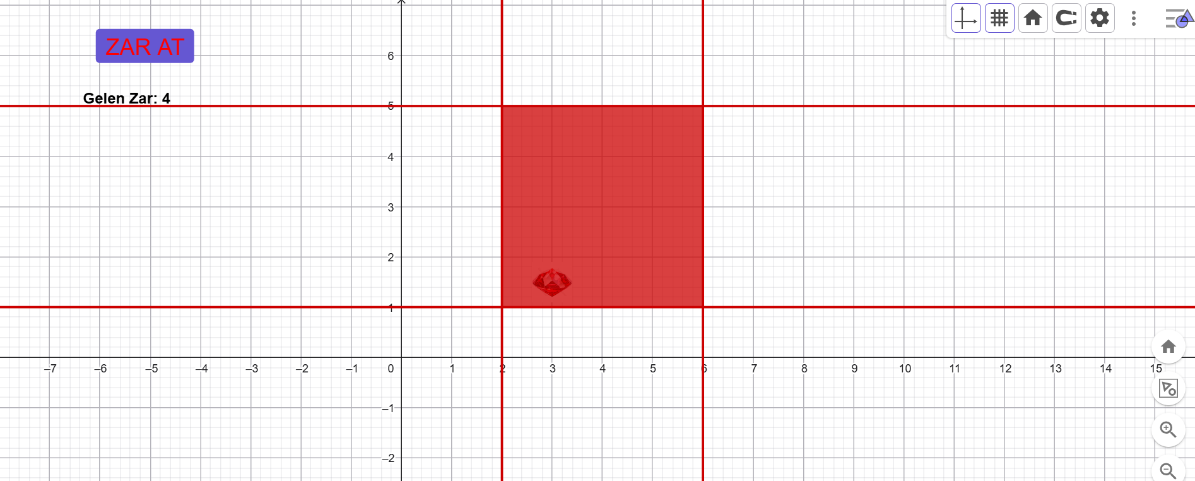
[b]c)Taralı alanı veren eşitsizliği yazınız.[/b]
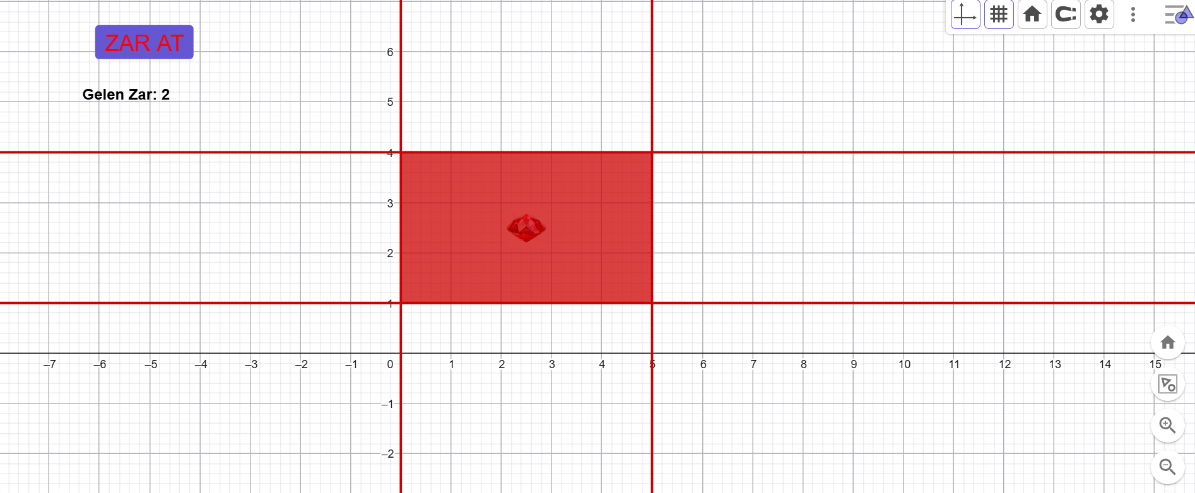
[b]d)Taralı alanı veren eşitsizliği yazınız.[/b]
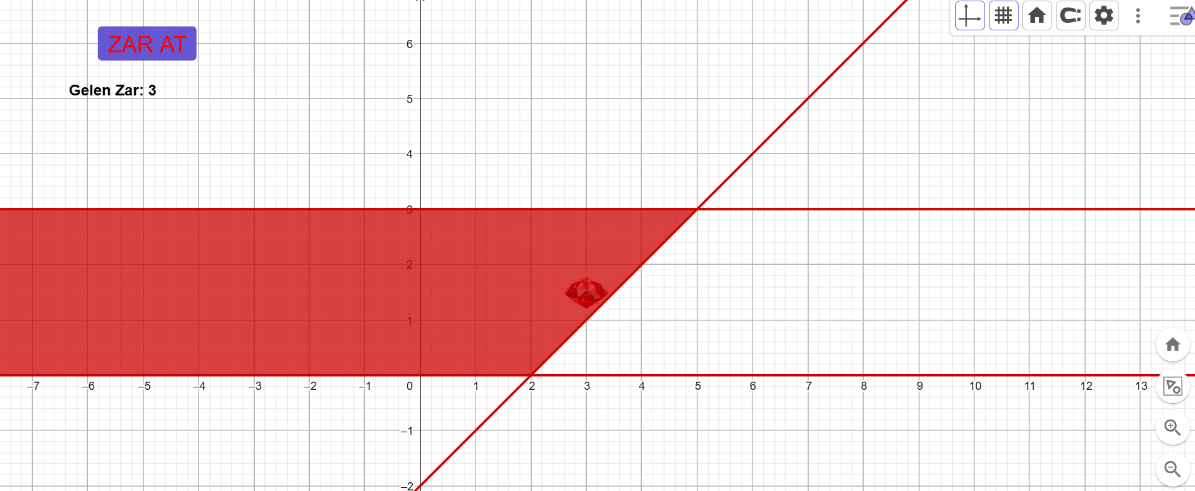
[b]e)Taralı alanı veren eşitsizliği yazınız.[/b]
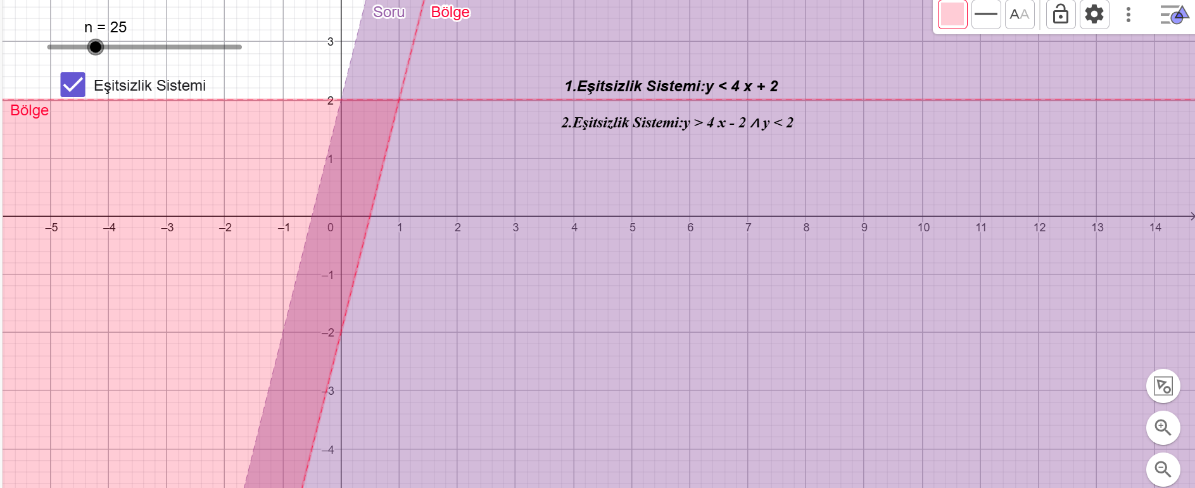
Soru-3
[b]Eşitsizlik sistemini belirtiniz.[/b]
Soru-4
Analitik düzlemde boyalı olarak verilen pembe bölgeyi tanımlayan [b]birinci dereceden iki bilinmeyenli eşitsizlik sistemini[/b] yazınız.
Soru-5
[b]Ekranda gördüğünüz taralı bölgeyi temsil eden matematiksel modeli eşitsizlikler cinsinden ifade ediniz. [/b]
[b][i]Bağlantı içerisinde, mutlak değer, denklemler ve eşitsizlikler konularına yönelik ölçme ve değerlendirme soruları yer almaktadır. [/i][/b]