Teorema de Pitágoras e Casos Semelhança de Triângulos
Table of Contents
- Introdução
- Introdução
- Quem foi Pitágoras?
- Atividade
- atividade 1
- atividade 2
- Questões
- Questão 1
- Questão 2
- Questão 3
- Casos de Semelhança de Triângulo
- introdução
- Atividade
- Semelhança de triângulos
- Semelhança de triângulos
- Questões
- questão 1
- Questão 2.
- Questão 3.
Introdução
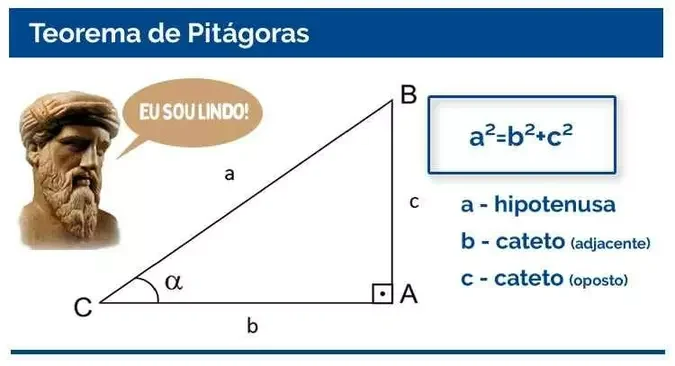
O Teorema de Pitágoras afirma que, em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. Sua fórmula é a² = b² + c². É usado para calcular um lado desconhecido quando se conhecem os outros dois, sendo fundamental na matemática e em várias áreas práticas.
atividade 1
Questão 1
Questão 1
Um poste quebrou-se a 4 metros de sua base, e sua parte superior atingiu o solo a 6 metros do pé do poste. Qual era a altura original do poste?[br]
introdução
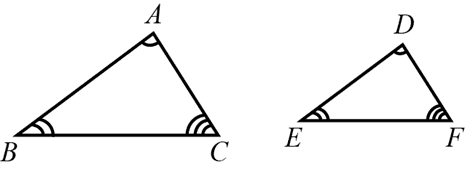
A semelhança de triângulos é um conceito geométrico onde duas figuras triangulares mantêm a mesma forma, possuindo ângulos correspondentes congruentes e lados homólogos proporcionais. Esta relação pode ser verificada através de três casos principais: o caso Ângulo-Ângulo (AA), onde a igualdade de dois ângulos é suficiente para estabelecer a semelhança; o caso Lado-Ângulo-Lado (LAL), que requer a proporcionalidade de dois lados e o ângulo entre eles; e o caso Lado-Lado-Lado (LLL), onde a proporcionalidade entre os três lados correspondentes garante a semelhança. Estas regras são fundamentalmente úteis para determinação de medidas inacessíveis, como cálculos de alturas e distâncias, sendo amplamente aplicadas em áreas práticas como topografia, engenharia e astronomia.
Semelhança de triângulos
Movimente o ponto que representa a medida da razão de semelhança (r) e responda as perguntas a seguir.
1.
Podemos dizer que os triângulos rosa e lilás são semelhantes?
2.
Se você respondeu sim à pergunta anterior, o que nos garante que eles sejam semelhantes?
3.
O que acontece quando a razão de semelhança é maior do que 1?
4.
O que acontece quando a razão de semelhança está entre 0 e 1?
5.
Um triângulo semelhante a estes tem seu maior lado medindo 20 cm. Podemos usar a propriedade de semelhança de triângulos para determinar a medida de um dos outros dois lados. Qual é essa medida?
questão 1
Os triângulos ABC e DEF são semelhantes, sendo ABC o triângulo maior. Sabe-se que:[br]AB = 12 cm, BC = 18 cm, CA = 24 cm][br]DE = 4 cm, EF = 6 cm[br]Qual é o comprimento do lado FD?[br][br]resolução: [br][br]Primeiro, identificamos a razão de semelhança (k) usando um par de lados conhecidos correspondentes.[br][code]AB[/code] corresponde a [code]DE[/code].[br](A razão é do triângulo menor para o maior).[br]Agora, usamos outro par de lados para encontrar FD. O lado FD do triângulo menor corresponde ao lado CA do triângulo maior.[br]FD / CA = k[br]FD / 24 = 1/3[br]FD = 24 * (1/3)[br]FD = 8 cm[br]Resposta: O comprimento do lado FD é 8 cm.