MOTO RETTILINEO UNIFORME
La lezione di approfondimento è rivolta agli studenti di una classe terza del Liceo Linguistico nell'ambito del corso di Fisica.
Table of Contents
- DEFINIZIONE
- DEFINIZIONE DI MOTO RETTILINEO UNIFORME
- Visualizzazione dinamica del moto rettilineo uniforme
- ESERCIZI DI APPLICAZIONE
- ESERCIZIO A
- ESERCIZIO B: Percorso a due velocità
DEFINIZIONE DI MOTO RETTILINEO UNIFORME
MOTO RETTILINEO UNIFORME
[justify]Il moto rettilineo uniforme è un moto rettilineo in cui la velocità media è costante in qualsiasi intervallo di tempo. In tal caso la velocità istantanea coincide proprio con la velocità media.[br]Nel caso in cui all'istante [math]t_0=0s[/math] il corpo si trova nella posizione iniziale [math]s_0=0m[/math] allora si può verificare che esiste una diretta proporzionalità tra spazio e tempo la cui costante è data proprio dalla velocità del nostro corpo. [br]La relazione [math]s=v\cdot t[/math] prende il nome di LEGGE ORARIA DEL MOTO[/justify]
PRIMO ESERCIZIO
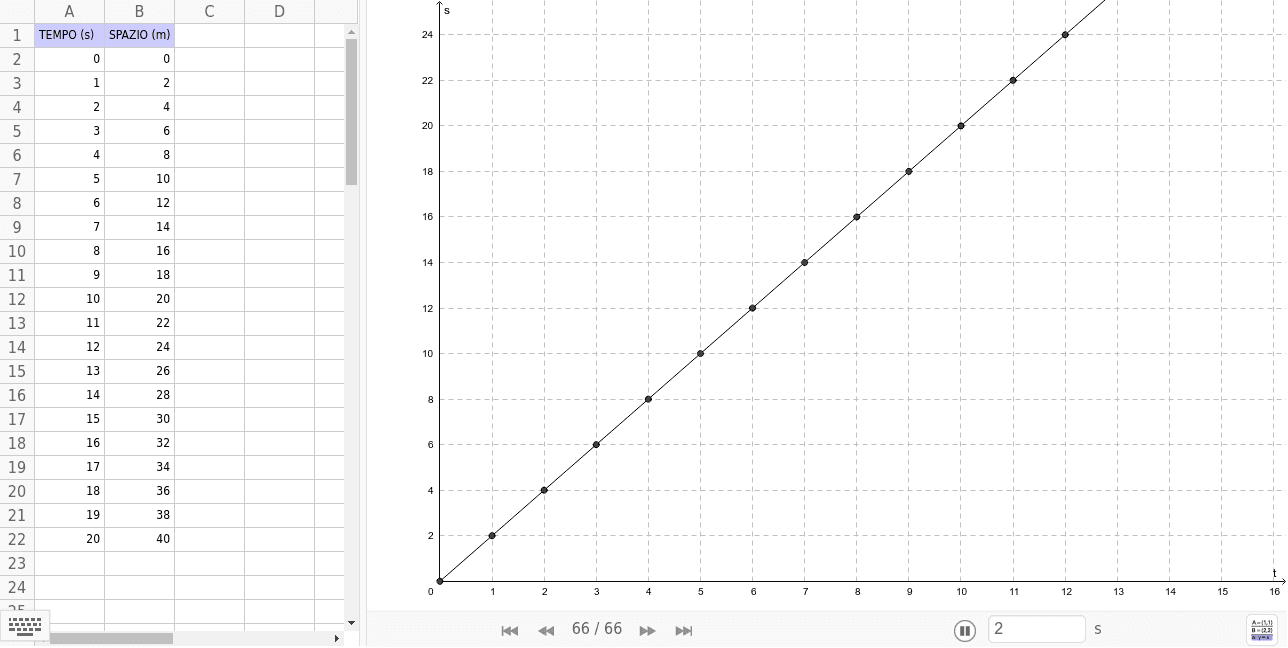
Il primo esercizio consiste nel mettere in luce la relazione di proporzionalità tra lo spazio e il tempo, considerando un punto materiale che si muove di moto rettilineo uniforme con velocità [math]v=2\frac{m}{s}[/math] che all'istante [math]t_0=0s[/math] si trova nella posizione iniziale [math]s_0=0m[/math]. Riportiamo in una tabella i tempi e le relative posizioni e tracciamo il relativo grafico.
Calcolare la posizione del corpo dopo 5 minuti ed il tempo impiegato per percorre 50 metri.
SECONDO ESERCIZIO
Consideriamo il caso in cui all'istante [math]t_0=0s[/math] la posizione iniziale del corpo sia [math]s_0=4m[/math]. La legge orario in tal caso risulterebbe: [math]s=s_0+v\cdot t[/math] e la relazione che lega lo spazio al tempo non è più una proporzionalità diretta bensì una dipendenza lineare. Proviamo quindi a tracciare il grafico spazio-tempo in tal caso.
Quale sarebbe in questo caso la posizione del corpo dopo 4 minuti? In quanto tempo riesce a percorrere una distanza di 60 metri?
In generale la relazione che lega lo spazio al tempo, la legge oraria del moto, può essere rappresentata da una equazione [math]y=v\cdot x+s_0[/math] che è quella di una retta il cui coefficiente angolare è proprio la velocità del corpo mentre l'ordinata all'origine rappresenta la posizione dello stesso all'istante iniziale [math]t_0=0s[/math].
Rappresentare in tal caso la relazione precedente con il relativo grafico ed osservare come si modifica il grafico spazio-tempo al variare di [math]v[/math] ed [math]s_0[/math]
ESERCIZIO A
Supponiamo che all'istante [math]t_0=0s[/math] un corpo A si muova con velocità costante [math]v_A=4\frac{m}{s}[/math] partendo dalla posizione [math]s_0=0m[/math]; nello stesso istante iniziale un corpo B che si trova nella posizione [math]s_0=6m[/math] inizia muoversi con velocità costante [math]v_B=2\frac{m}{s}[/math]; rappresentare le leggi orarie relative ai due corpi ed i grafici spazio-tempo ed individuare graficamente l'istante in cui il corpo A raggiunge il corpo B.