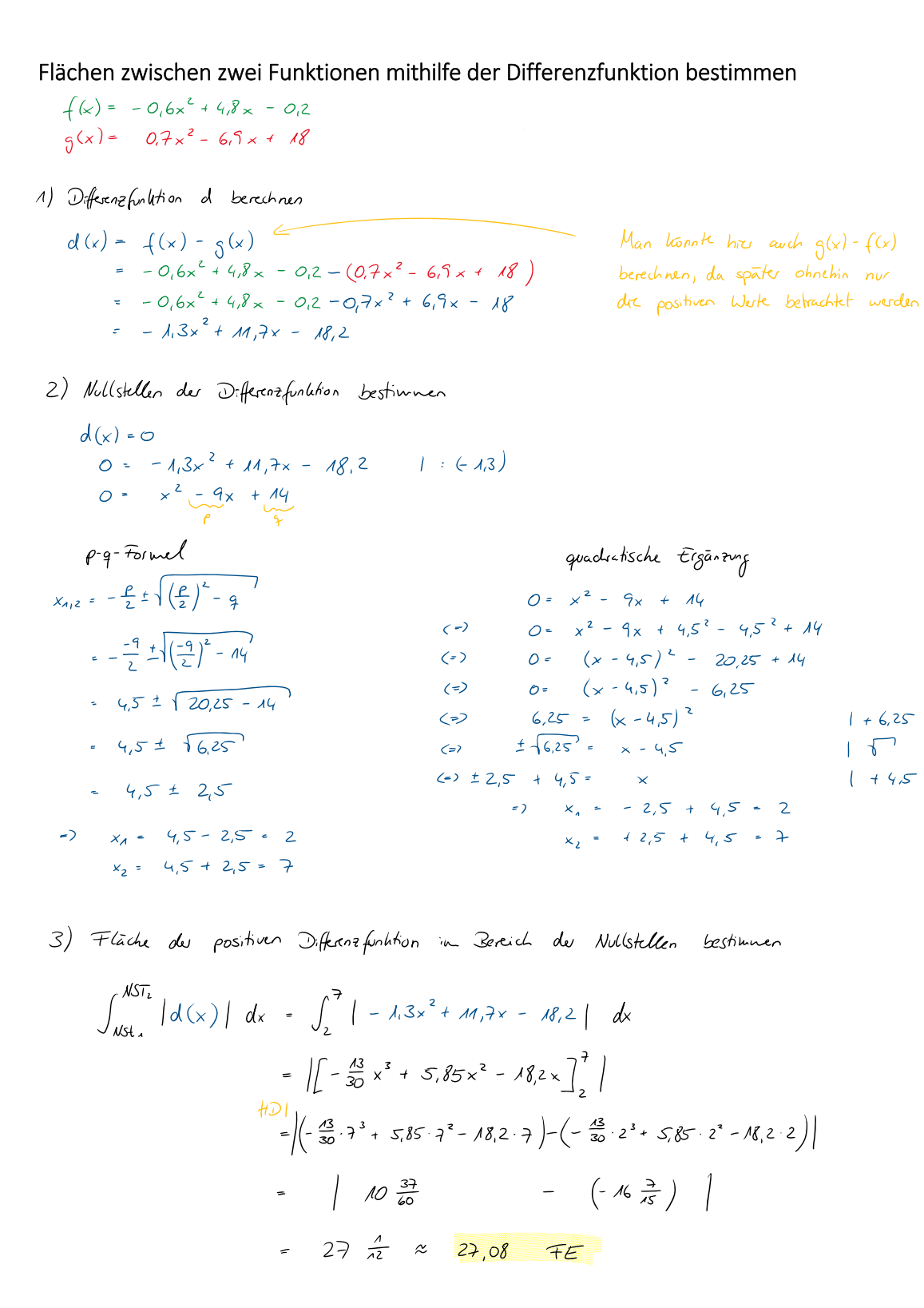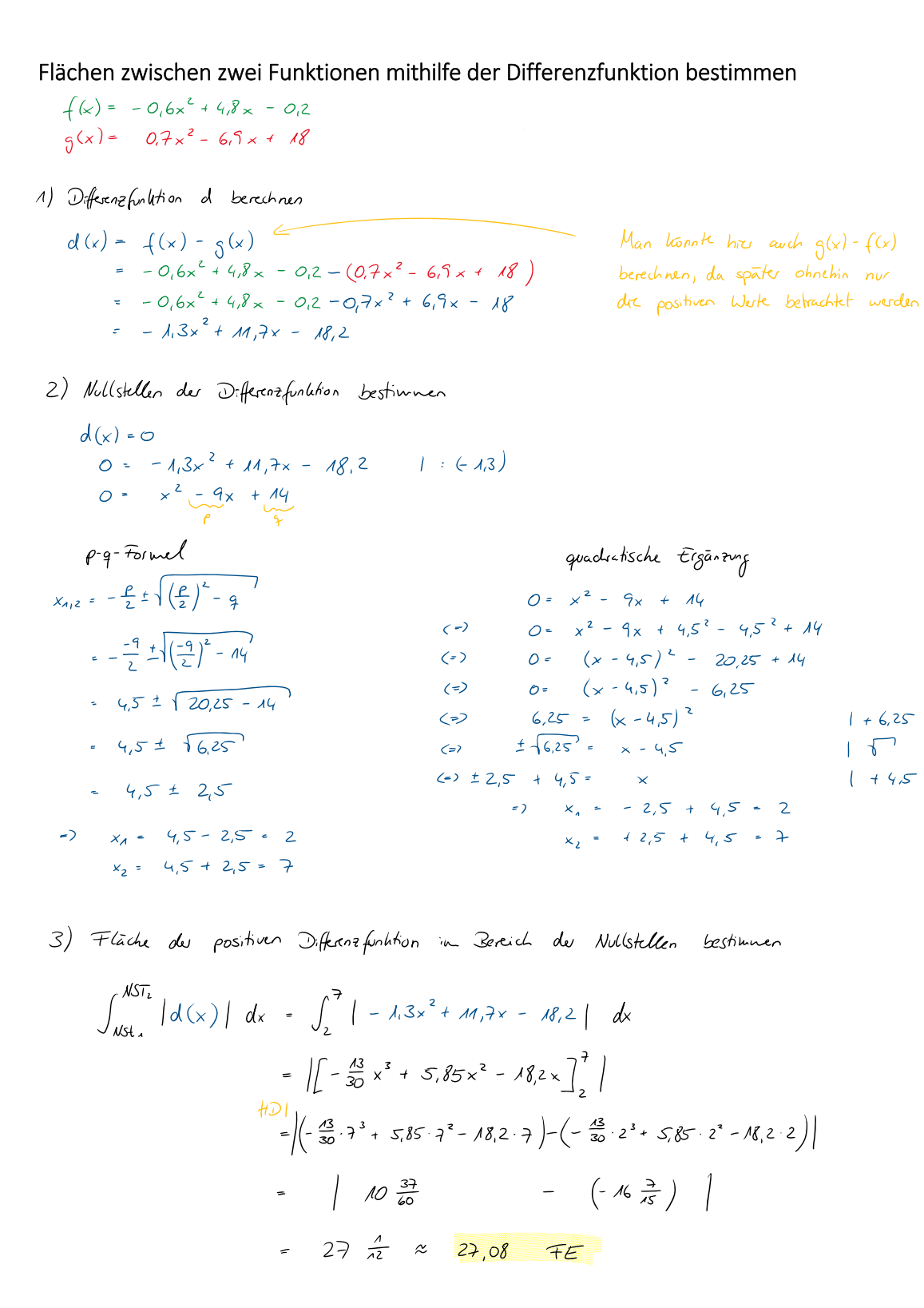
von der Differenz zweier Funktionen zur Differenzfunktion
[list][*]Gleichsetzen[/*][*]Schnittpunkte berechnen[/*][*]Fläche innerhalb der Schnittpunkte vom Betrag jeder Funktion mithilfe des Integrals bestimmen[/*][*]Flächenwerte voneinander subtrahieren[/*][/list][br]Die bisherige Berechnung der Fläche zwischen zwei Funktionen bestand aus vielen kleinen Schritten. Wäre es da nicht viel schöner, wenn man all diese Schritte mit bereits bekannten Verfahren lösen könnte?[br][br]Hier die gute Nachricht: Das geht! Anstatt die Differenz der beiden Flächen zu berechnen, betrachten wir mal die Fläche, die wir berechnen wollen.[br]Flächen kann man für kleine Bereiche als Rechtecke annähern, die das Produkt aus Höhe und Breite sind. Bei der Fläche zwischen zwei Funktionen sind die Randbereiche zwar nicht rechteckig, aber auch hier setzt sich die Fläche aus Breite und Höhe zusammen.[br]Speziell die Höhe soll nun näher betrachtet werden. Rein graphisch sind die Längen der Höhen, die in der Grafik unten als einzelne Höhenlinien eingezeichnet sind, nicht zu beschreiben. Es lässt sich jedoch erkennen, dass am Schnittpunkt der beiden Funktionen kein Höhenunterschied besteht, die Länge der Höhe dann zunimmt, zwischen den Extrempunkten der Funktionen am längsten erscheint und dann wieder abnimmt.[br]Höhenwerte haben wir bisher immer über die y-Werte einer Funktion bestimmt. Dies war aber nur möglich, weil immer der Abstand vom 0-Wert - also der x-Achse bestimmt werden musste. Hier beginnt die untere/obere Kante der Fläche aber nicht die x-Achse, sondern eine andere Funktion. Um das aktuelle Problem so zu verändern, müssen sozusagen alle Höhenlinien so weit im Koordinatensystem herunter/raufgezogen werden, bis sie mit einem Ende auf der x-Achse liegen.[br]Dieser Prozess soll nun grafisch dargestellt werden. Starte die Animation in der Grafik unten und beobachte, was passiert. Achte dabei besonders auf die schwarzen gestrichelten Distanzlinien.
Du konntest beobachten, dass die rote Funktion sozusagen "auf die x-Achse heruntergezogen wird". Dabei sind die Längen der Höhenlinien aber immer gleich geblieben, sodass sich auch die Lage des grünen Funktionsgraphen verändert hat.[br]Als dann die rote Funktion auf der x-Achse lag, hatte sich die grüne Funktion so verzerrt, dass sie zu einem neuen Funktionsgraphen wurde (blau). Da die Länge der Höhenlinien aber die ganze Zeit gleich bleiben, kann der Abstand zwischen der ehemals grünen und roten Funktion, über die y-Werte der blauen Funktion berechnet werden. Da am Schnittpunkt der roten und grünen Funktionsgraphen der Abstand 0 war, besitzt der blaue Funktionsgraph an dieser Stelle y-Werte von 0 - es handelt sich hier also um die Nullstellen der Differenzfunktion.[br][br]Jetzt magst du vielleicht befürchten, dass diese Verzerrung mathematisch hochkomplex ist, genau das Gegenteil ist aber der Fall:[br]Die Länge jeder Höhenlinie startet an jeder Stelle bei dem zugehörigen y-Wert der roten Funktion und endet beim zugehörigen y-Wert der grünen Funktion - ist also berechenbar über den Abstand der Funktionen an jeder einzelnen Stelle. Dieser Abstand kann berechnet werden, indem du an jeder Stelle den y-Wert der roten Funktion vom y-Wert der grünen Funktion abziehst. Weil diese Differenzbildung aber an JEDER Stelle durchgeführt werden müsste, kann man alternativ auch einfach die Differenz der beiden Funktionsgleichungen berechnen, denn diese ergeben ausgewertet an jeder Stelle ja die zugehörigen y-Werte. Diese neue Funktion nennen wir "Differenzfunktion".[br]Der blaue Funktionsgraph muss also der Graph der Differenzfunktion sein. [br][br]Damit haben wir das Verfahren gefunden, welches gleichwertig zur Betrachtung der Fläche zwischen zwei Funktionen ist, jedoch nun die Fläche zwischen einer Funktion und der x-Achse betrachtet werden kann. Das war bisher immer über das Integral einer Funktion im Bereich der Nullstellen möglich.[br][br]Was bedeutet das also für die Flächenberechnung zwischen zwei Funktionen? Zusammengefasst lassen sich folgende Schritte formulieren:[br][list=1][*]Differenzfunktion bilden ([math]f\left(x\right)-g\left(x\right)[/math] berechnen, im folgenden [math]d\left(x\right)[/math] genannt)[/*][*]Nullstellen der Differenzfunktion berechnen ([math]d\left(x\right)=0[/math])[/*][*]Fläche unter der positiven Differenzfunktion im Bereich der Nullstellen bestimmen ([math]\int_{NSt1}^{NSt2}\left|d\left(x\right)\right|dx[/math])[/*][/list][br]In der untenstehenden Abbildung kannst du diese drei Schritte nun nochmal praktisch durchgeführt beobachten.