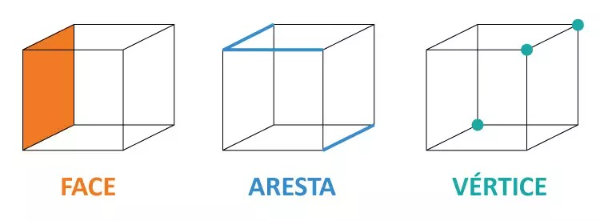
[justify][size=100][/size][/justify][justify][size=100]Os poliedros são [color=#ff0000]sólidos geométricos[/color], formas com [color=#ff0000]três dimensões[/color], limitados por um número finito de polígonos planos. Esses polígonos formam as faces do poliedro. A intersecção de duas faces é chamada de [color=#ff0000]aresta[/color] e o ponto comum de três ou mais arestas é chamado de [color=#ff0000]vértice.[/color][br][br][/size][color=#ff0000]OBS:[/color] Para ser considerado um poliedro, a forma não deve possuir faces curvas. [size=100]Os poliedros são classificados como convexos ou não convexos e podem ser regulares (com todas as faces e ângulos iguais) ou irregulares.[/size][/justify]

[b]Poliedros regulares:[/b] os sólidos de Platão[br][br][justify]Existem cinco corpos geométricos chamados sólidos platônicos porque foi Platão quem os estudou primeiro. Esses cinco corpos sólidos compartilham certas características e também são frequentemente chamados de sólidos perfeitos ou corpos cósmicos.[br]Suas principais propriedades são que todas as suas faces são formadas por polígonos regulares idênticos, seus ângulos diedros (junção espacial formada por dois semiplanos com uma reta em comum) são iguais, as arestas têm a mesma medida de comprimento e o mesmo número de faces e arestas concorrem em direção aos vértices.[/justify][br]Existem apenas cinco poliedros regulares convexos, designados por “Sólidos Platônicos” ou “Poliedros de Platão”. São eles: tetraedro, hexaedro (cubo), octaedro, dodecaedro, icosaedro. Iremos estudar cada um detalhadamente nos próximos capítulos. [br][br][list=1][*][b]Tetraedro: [/b]sólido geométrico formado por 4 vértices, 4 faces triangulares e 6 arestas.[/*][*][b]Hexaedro: [/b]sólido geométrico formado por 8 vértices, 6 faces quadrangulares e 12 arestas.[/*][*][b]Octaedro[/b]: sólido geométrico formado por 6 vértices, 8 faces triangulares e 12 arestas.[/*][*][b]Dodecaedro:[/b] sólido geométrico formado por 20 vértices, 12 faces pentagonais e 30 arestas.[/*][*][b]Icosaedro:[/b] sólido geométrico formado por 12 vértices, 20 faces triangulares e 30 arestas[/*][/list]

[b]Poliedros Irregulares:[br][/b][b][br][/b]Poliedros irregulares são aqueles que têm faces que são polígonos, mas não todos iguais.[br]Com isso queremos dizer que, ao não cumprir a regularidade, eles serão compostos por polígonos que não serão regulares e, portanto, não serão idênticos entre si. Sua classificação ou denominação depende das faces do poliedro.[b][br][br][br]Os poliedros irregulares mais conhecidos são:[br][br][br][/b][list=1][*][b]Tetraedro: [/b]o tetraedro é um poliedro composto por quatro faces que são polígonos irregulares, ou seja, elas são diferentes entre si.[/*][*][b]Tetraedro triretangular:[/b] O tetraedro triretangular é um poliedro formado por três triângulos retângulos, ou seja, possui três ângulos retos que possuem o mesmo vértice.[/*][*][b]Tetraedro isofacial:[/b] O tetraedro isofacial é um poliedro formado a partir de uma base que é um triângulo retângulo e três faces que são triângulos isósceles idênticos.[/*][*][b]Pentaedro:[/b] O pentaedro é um poliedro composto por cinco polígonos irregulares.[/*][*][b]Hexaedro:[/b] O hexaedro é um poliedro cujas faces são seis polígonos diferentes entre si.[/*][*][b]Heptaedro:[/b] O heptaedro é um poliedro formado por sete faces diferentes, ou seja, os polígonos que o formam são irregulares.[/*][*][b]Octaedro: [/b]O octaedro é um poliedro composto por oito polígonos que são diferentes ou irregulares.[/*][/list]Existem outros poliedros irregulares, porém ao longo de nosso estudo, aprenderemos cada um por parte.

[size=100][justify]Os poliedros podem ser classificados como convexos ou não convexos. Um poliedro é considerado convexo se qualquer segmento de reta que conecta dois pontos em seu interior estiver completamente contido dentro dele.[br]Outra maneira de identificar um poliedro convexo é observar que qualquer reta que não esteja contida em nenhuma de suas faces nem seja paralela a elas intersecta os planos das faces em, no máximo, dois pontos.[/justify][/size]Abaixo, temos os poliedros nas cores, Laranja, Rosa e Verde Claro, como Poliedros não convexos, se repararmos bem, temos um segmento que passa por dois pontos desses poliedros, porém não estão totalmente contidos em seu interior. Por outro lado, o cubo (Verde), o tetraedro (Vermelho) e o Icosaedro (Roxo), temos um segmento de reta que estão contidos totalmente em seu interior e por isso mesmo, poliedros regulares e convexos.