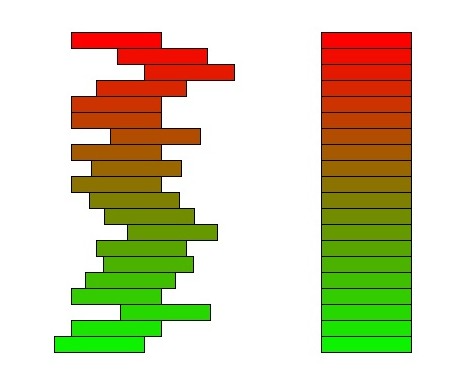
Cavalieri's Principle is a principle used to show equality in area or volume between two geometric regions that share certain properties. It gets its name from its creator, Bonaventura Cavalieri, though it was known at the time of its conception as the method of indivisibles. [br][br]The method works as follows:[br][br]2D - If two figures between two parallel lines have the property that every line parallel to these boundary lines intersects both figures in segments of equal length, then the two figures have the same area.[br][br]3D - If two solids between two parallel lines have the property that every plane parallel to these boundary lines cuts both solids into cross-sections of equal area, then the two solids have the same volume.

Credit: Irina Boyadzhiev [br]Link: geogebra.org/m/auHB2YWq

Statement to Prove: [br]Suppose two plane figures, [math]A[/math] and [math]B[/math], are contained between two fixed parallel lines. For simplicity, say these lines are [math]y=a[/math] and [math]y=b[/math]. Then if every line parallel to these boundaries, [math]y=c[/math] with [math]a\le c\le b[/math] intersects [math]A[/math] and [math]B[/math] in segments of equal length, the areas [math]A[/math] and [math]B[/math] are equal.[br][br]Proof:[br]At any height [math]y=c[/math], let the length of the intersection with figure [math]A[/math] be [math]f\left(c\right)[/math] and with figure [math]B[/math] be [math]g\left(c\right)[/math]. By assumption then, [math]f\left(c\right)=g\left(c\right)\forall c\in\left[a,b\right][/math]. Now, divide the interval [math]\left[a,b\right][/math] into [math]n[/math] subintervals of equal height [math]\bigtriangleup y[/math]. Then the area of subinterval [math]i[/math] would be [math]f\left(y_i\right)\Delta y[/math] and [math]g\left(y_i\right)\Delta y[/math] where [math]y_i[/math] is a sample point in the subinterval. Therefore, the total areas would be approximated as follows:[br][br][math]\left(A\right)\approx\sum^n_{i=1}f\left(y_i\right)\Delta y[/math][br][math]\left(B\right)\approx\sum^n_{i=1}g\left(y_i\right)\Delta y[/math][br][br]Since [math]f\left(y_i\right)=g\left(y_i\right)[/math] for each [math]i[/math], the approximations are equal. Going a bit further, if we take the limit as [math]\bigtriangleup y\longrightarrow0[/math], we end up with the definite integrals:[br][br][math]\left(A\right)=\int^b_af\left(y\right)dy[/math][br][math]\left(B\right)=\int^b_ag\left(y\right)dy[/math][br][br]and since [math]f\left(y\right)=g\left(y\right)\forall y\in\left[a,b\right][/math], the areas [math]A[/math] and [math]B[/math] are equal.[br][br]The proof for 3D can be done through a similar approach, but with each subinterval being a volume instead of an area, taking the integral of the area of stacked planes as the height of each subinterval reaches 0.

Cavalieri wrote his principle of indivisibles in 1629, but integrals weren't a concept until the 17th century, so how come we have to use them in our proof? The short answer - Cavalieri was afraid of persecution.[br][br]The idea of space being made up of indivisible elements was highly controversial because:[br][br]- It was a hard concept to reconcile with the traditional Aristotelian view of space. Critics argued that without a precise definition of infinitesimals, the method could lead to contradictory results or paradoxical conclusions. [br][br]- The Church held significant influence over mathematical and scientific discovery. Some worried that a continuum made up of indivisibles could undermine established theology about the nature of creation.[br][br]Because of this, Cavalieri very carefully avoided ever stating outright that the continuum was composed of indivisible elements. [br][br][br]As a result, his "proof" for this principle was not rigorous by today's standards. It was more of an exhaustive example using approximations with smaller and smaller areas, implying, but never stating outright, that if you were to continue that process infinitely, you would eventually get an exact result. [br][br]Because of this fear of persecution, he never actually used this principle to find any unknown (at the time) results, which is a shame because he may have invented the concept of integration long before Newton or Leibniz if he had. He might be considered the father of modern-day calculus.