Classificação Geométrica de Sistemas
Introdução
Com a atividade seguinte pretende-se que, com a ajuda do Geogebra, consigas classificar geometricamente, sistemas de equações.[br]Segue as etapas seguintes.[br]Vai registando as respostas na tua folha.
1.
Na janela do Geogebra, move o seletor [math]a_1[/math] para [math]2[/math]; [math]b_1[/math] para [math]3[/math]; [math]a_2[/math] para [math]-3[/math] e [math]b_2[/math] para [math]2[/math].
1.1.
Qual a posição relativa das retas?
1.2.
As retas têm algum/alguns ponto/s em comum? Se sim, qual/quais?
1.3.
Ativa a caixa de seleção "Classificação do sistema" e confirma as tuas conclusões.
2.
Move o seletor [math]a_1[/math] para [math]-1[/math]; [math]b_1[/math] para [math]4[/math]; [math]a_2[/math] para [math]-1[/math] e [math]b_2[/math] para [math]-1[/math].
2.1.
Qual a posição relativa das retas?
2.2.
As retas têm algum/alguns ponto/s em comum? Se sim, qual/quais?
2.3.
Ativa a caixa de seleção "Classificação do sistema" e confirma as tuas conclusões.
3.
Move o seletor [math]a_1[/math] para [math]3[/math]; [math]b_1[/math] para [math]2[/math]; [math]a_2[/math] para [math]3[/math] e [math]b_2[/math] para [math]2[/math].
3.1.
Qual a posição relativa das retas?
3.2.
As retas têm algum/alguns ponto/s em comum? Se sim, qual/quais?
3.3.
Ativa a caixa de seleção "Classificação do sistema" e confirma as tuas conclusões.
Conclusão
Após os resultados obtidos nas questões anteriores, podemos concluir que:
I
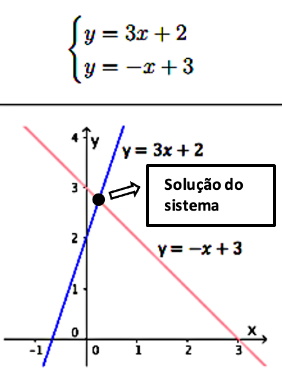
a) Se as retas são concorrentes, o sistema é:
b) A solução é o ponto de:
c) O sistema tem (número de soluções):
Exemplo:

II
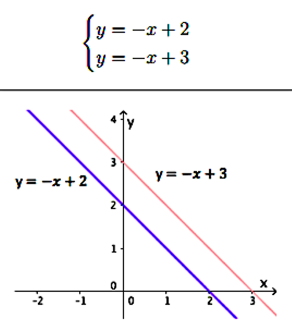
a) Se as retas são estritamente paralelas, o sistema é:
b) As retas ______________________ pontos em comum:
c) O sistema tem (número de soluções):
Exemplo:
III
a) Se as retas são coincidentes, o sistema é:
b) As soluções são:
c) O sistema tem (número de soluções):
Exemplo:
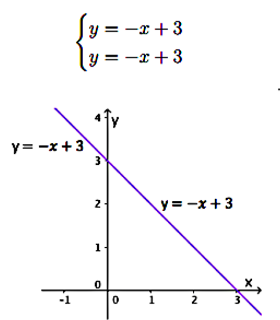
Se ficaste com dúvidas e/ou pretendes fazer uma última revisão, visualiza o vídeo seguinte: