IM Geo.5.15 Lesson: Putting All the Solids Together
Evaluate the volume of each solid mentally.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAG8AAAB6CAYAAACx3g1IAAALaElEQVR4Ae1dCUgVXRR2qV9LbaFMKtosXCotWzTKdjLKNlosK0qixIo2UlqIVioqMGmxDCqKoAWkICoLW0jDBG23zSJcwCKsSFpNz893YR6jzrz3Zt7iPD0XHjN3mbn3nu989557580cN+LgshJwc9mWc8OJwXNhJWDwGDwXloALN52Zx+C5sARcuOnMvOYIXllZGd29e5d/Mhk4Ww90Me/r168UEhJCbm5u/JPJICkpyan46QYPwHl5edHYsWOpqqrKqY1u7MoKCwsJQLVp04b+++8/iouLo6ioKFq0aJFTm2YTeBkZGRQQEEB9+/alkpISpzbc2ZV9//6d0tPTadCgQWK0CQsLo7S0NKqsrBRNmTJlCi1evNipzbIJvFu3blF5eTmFh4dTx44dqaCgwKmNd0Zlubm5lJCQQK1btyY/Pz9KTEyk/Pz8BlW7JHjoxY8fP2jixInk7e1NV69ebdAxV0sAm1JTUyk0NFSwLDo6mk6fPi36qdYXlwUPHaqpqaHVq1eTu7s77du3T62Phk2vra2l7Oxsmjt3rpjHMB2kpKRQcXGxVW12afCkHp44cYI8PDzE5P3v3z8p2bDHT58+0e7duykwMJA8PT0pNjaWLl++TNXV1Zra3CTAQ4+zsrLEHAFL9Nu3b5qE4IzCUCoM79OmTROA9e7dWwBYUVGhu/omAx4k8PTpU+ratSsFBQUZxhItLS2lLVu2iHZhfl6wYAHduXOHMGTaGpoUeBDGx48fG90S/fv3L126dIliYmLEfBwREUFHjhyx+4jQ5MADgHJLNDMz01YFt/p6GBrJycnk7+9P7dq1oxUrVtCjR4+svl5rwSYJHoQAS3TNmjVC8/fu3atVLlaX//37N505c4ZGjhwp6hozZgydO3eOkO7o0GTBkwTnKEv02bNntHLlSsGwLl260ObNm+n9+/dStU45NnnwIEVYor6+vmJP1BZLFPup2J4bMmQItWjRgmbMmCEsyMZanjQL8ABgUVGRbks0Ly+PlixZQj4+PhQcHCw2BLBWa+zQbMCDoOWW6MOHD83KHo+gsAncv39/sX7EBnBOTo7Za5yd2azAg3BhiaLTeKyiZIliDRYfHy8ePQ0dOlQMk9jdN2JoduBJIKxbt05sAO/Zs4cwBMIi7dOnD3Xo0EFYqRhmjR6aLXgA5vjx46an8uPHj6cLFy4YHa867WvW4EESkZGRtHDhwjpCcZVIswcPG9nLly93FbzqtJPBY/DqKISliM1/g7BUgZZ8Zp4WaZG+t4Sw7sK/x/AfFnsGBk+bNJl52uSlWprnPJ7zVJVDKYOZpyQVHWnMPGaeJrVh5mkSl3phZh4zT107FHKYeQpC0ZPEzGPmadIbZp4mcakXZuY1ceYdPHhQPJ9UUgG8ZYz/4eAfbzg+fvxYqVidNGZeHXHoj5hjHrYTAUiPHj1o9OjRDSr58OGD+Ofbtm3bxGviOLZt25aQbi4weOakoyHPHHgDBgwQL16CXUrg4T8506dPr1Mb0iy9rMng1RGZ/og58MA8BDXwwEi8/ycPiPfs2VOe1OCcwWsgEn0J5sCT7qgGHp7QIE8eEEe6uWA+V+VKfiTUUDAMXhO3Npl5DZXeECm2MA+WJd7GlQfEediUS8SB57aAB0sTb1HJA+JKlqm8DM95cmnYcG4LeBhOwT5pYY4j3imsb4HWbx6DV18iOuO2gIcqARQAxFCJHxbqlgKDZ0lCVuZbA541t7K0qyK/B4Mnl4YN5/YCT0sTGDwt0jJTlsFr4us8M9jrymLm6RJbw4uYecy8hlphJoWZZ0Y4WrKYecw8LfrCL5pokpaZwsw8Zp4Z9WiYxXNeQ5noSmHmMfM0KQ4zT5O41Asz85h56tqhkMPMUxCKniRmHjNPk94w8zSJS70wM4+Zp64dCjnMPAWh6Eli5jHzNOkNM0+TuNQLM/OYeeraoZDDzFMQip4kZh4zT5PeMPM0iUu9MDOPmaeuHQo5zDwFoehJYuYx8zTpDTNPk7jUCzPzmHnq2qGQw8xTEIqeJGYeM0+T3jDzNIlLvTAzj5mnrh0KOcw8BaHoSXIp5oWGhlKrVq1M/UxPT6dOnTqZ4ocOHaLOnTub4qmpqdStWzdT/MCBA3U+zwTPXbif5I5m165dFBISYiq/fft24T9PSoDLbHzTSwobN26kwYMHS1FKSUmhqKgoUxyewoYPH26Kr1q1ikaNGmWKwyHwuHHjTPHExESaMGGCKQ6Hi5MmTTLF8V2wqVOnCvemGzZsED5qLX0rzHSxnU50MQ91Qzh48X3Hjh2iKfDRCsfxUnj37h1du3ZNitLbt2/p+vXrpvibN2/oxo0bpvjr168FGBJ4r169ops3b5ryX758WccJx4sXLyg7O9uU//z5c7p9+7YpDj+y8L8nBfhtl38i6smTJ3Tv3j0pW3yJ4f79+6Z4YWFhHQeLBQUFlJuba8qHMkF5IIOAgACKi4sT/gBNBZxwohs8tA2ekT09PWnevHkEf+S2BqN7NAGAUC58tcEIfmptAg9gQbvRmejoaPry5YtN+BkRPDglPnz4MA0cOFCwLCgoyDB+am0GD2hhCOzevTsFBgba5OLaKODV1taKIXj+/Pnk7e1tWD+1dgEPAH7+/FkYDO3btydLDnzV6NnY4FVUVBAMJSgh5jKj+6m1G3gA5NevXzRz5kzhwPf8+fNqGKmmNwZ41dXVwtnw5MmTxfztSn5q7QqehApMZ2s/wSRdg6MzwSsuLqbk5GSxvHF3dxfLAvip/fPnj7xJhj53CHjosdwStVYgjgYPrr1PnTpFI0aMEMqFdefWrVuptLTU0CCpNc5h4KFCyRLFYtkaS9RR4GEOXrZsGfn5+Ykhffbs2ZSVlUU1NTVqcnGJdIeCBwlosUTtCV5lZSVhV6dfv36CZTgijvSmEhwOHgQlt0RzcnJUZWcreDDxwag5c+YIhvn6+tLSpUspLy9PtU5XznAKeBCQZIm2bNmS1CxRveBhzsL3KbHWhKGEPcyTJ086fbvK2YrgNPCkjm3atEkIGIaCPMCoCQ8Pp2HDhhH2OS0FbMddvHiRYmJiyMPDg/z9/Wn9+vVWXWvp3q6S73TwIBhYomAg9kQB2oMHD2jnzp0UFhZGs2bNIgCMjWWlUFRURGvXriWsxwAadvozMzMJ67XmFnSBh9157KqnpaWZvousVXCY+7AnCm8eR48epbKyMtM6D08kwEzs7CNUVVVRRkYGRUZGCtb26tVL7ISUl5drrdZsefiLuHLliuib/ImD2YsaMVMTePiELlykQOB4doWvkgOAhIQEXV2AJYpnftiOwrl8zispKRHGRmxsLPn4+JCXlxfFx8eLx0AwTOwdpI9y44vqmD9xRF8lVzL2rs8e99MEHiqs//1/dBpGgvRlcq2NgiWKdSCUICIiQijC/v37KTg4WNwXD33xYNfRQpSUUd5+CUh5mpHONYOn1HiAJ3/QqVTGUhrmP9wHP5j4SUlJlJ+fb+kyu+Ur+TYAoPX9HditQjvcyGbw4NAPrLEHM44dO0Znz56lnz9/2qFr2m6BEQX9kJQQR8T1jijaatdXWhd40EZ4WMScAI3V8jl5fc10zlWSCxhpXjcycJCILvDgwAGTOn4wXuCV0R7Mcw5EyrWg/XhaDmXEaIJ+QUGN3C9d4Mm7j86ho+iwKwcYJ/L5Df0CkPgZNdgMHjpWv+NG7ay5dikZXZj3kG7UoKllSkMI0jBHuDrzYJzUd7yEPsn/G2o0EDWBhzkO8wK2p7DDgiO8TRl5aLFW4JIjJqlv2HiQW5/W3seZ5TSBh4bBIpOMFRyNbpFpESasZqlvYJ3SSKPlfo4uqxk8RzeI72+9BBg862VluJIMnuEgsb5BDJ71sjJcSQbPcJBY3yAGz3pZGa4kg2c4SKxv0P9dizj0ihExjwAAAABJRU5ErkJggg==[/img]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAHcAAAB9CAYAAACYovzsAAAOP0lEQVR4Ae2da6gWRRjHRUxMiso0RUtDKemD+MEPQSgqYioiiloaKd4ozXNOaV4yU/N+1+4XKy3vKUWJqEF5+Rhomt+UON5ABa+pgVnaxG/jOc27573M7LuX2fV9YNnduT77/Oc/Mzs7M9tAVSSzFmiQ2SerPJiqgJvhQlABtwJuhi2Q4Ue765jbqlUr1bx58wxD+v+j3VXgbtu2TTVo0MA7tm7d+r8VMnp1V4HboUMHxdG+fXvvfOfOnYzC+t9j3TXgbtmyRTVu3FgNGDBA9e/f37veuHFjBdy0WwCGwtgJEyaoo0ePql9//VVVVVVlnr13BXM3b97sMfX8+fN15ZRrmLxhw4Y6t6xdZB5cYe3EiRPrYVddXZ1p9mYeXNpVGKqzVlAW9q5fv16cMnXONLjCWtpXkbffflu99dZbcqteffXVzLI30+DSnvpZO2zYMDVkyJA6cIW9X375ZZ1bVi4yC66wtqamJgcrP7h4vvbaa+qxxx5Tt2/fzgmb9pvMgvvVV1/VYy1g5QMX9jZp0kStW7cu7Xjm6J9JcGEg77W0p345ceKEqq2t9TuryZMnZ469mQSX9tPf1tZD0+dw6dIlj71r1671+aT3NnPgwlraT9pRW3n99dczxd7MgQvzaD9hoq0Iez///HPbqE6GzxS4wlraz0ICO/O1xRJ+ypQpmWFvpsD94osvSrI2X29ZgOUs7P3ss89051ReZwZcYS3MLCalwCXutGnTMsHezIBLO2nS1pqAK+z99NNPi5UT5/0yAa6wdurUqSUNfvHiRXXhwoWS4aZPn+6x99atWyXDuhogE+CuWbPGiLU2IAh7P/nkE5toToVNPbjCWtrJsOWNN95QzJZMK3tTDy7toklbGwT433//Xd13333q448/DhI98TipBhdGwSwYZiovvfSSGjNmjGlw9eabb6aWvakGF0bBLNpHUzHpLetpCXs//PBD3TkV16kFV1g7Y8YMK0PbgkviM2fOTCV7UwvuRx995LEWZtlIEHCFvR988IFNVomHTSW4wlraQ1v5888/1c2bN22jefOu0tZzTiW4tH+0tbastUZUiyDsff/99zVXty9TB66wVp/BGJeJZ8+enaq2N3Xgwpy4WSuFR9j77rvvipPT51SBK6ydNWtWYKMOHz5cDR06NHD8OXPmeOwN0m4HzjRgxFSB+95775XN2iC9Zd22wt533nlHd3byOjXgCmthTjlSLrjkzaqFhx9+OFCvuxzdbeOmBlyYEkZbO2LECPXCCy/Y2ikn/I0bN9QDDzygVq9enePu2k0qwKV9gykwxhWZN2+e8+xNBbgwBKbE+V5bqhAJe1euXFkqaGL+zoMrrIUprsn8+fOdZq/z4MIMWAtTwhDSCTMtdFuxYkUYqoWehtPgCmthSFgSRm9Z12XBggXOstdpcGFEmKwFlLDBlbZ3+fLlOuZOXDsLrrAWZoQppuCePHlSsQx07ty56rvvviuqwqJFi5xkr7PgwoSwWQtCr7zyinr55ZeLgsUiMnaa6969u/f6VeoVTNi7dOnSounG7ekkuMJaGBG3MFjSrl07deTIEausFy9e7LE3rM6aVeYFAjsJLgyIgrUFbJDjDLBB9scQ9i5ZsiQnvSRvnAMXIzEaBRPiFthKdYzQ5h44cEBdvXrVWA2ATapQ5lPSOXCjNtC5c+fU2bNn89nC6zgBzqhRo1Tnzp29Npf7SZMm5Q3vd5TmJImC6deFe6fAlaotyo5Jsd4yHSeYq1fLMBiAS/WYxbjLli1zhr1OgRvHK0UxcAGQNtcvAwcONP5oIexduHChP5nY750BV1hLyY9SioG7f/9+9eCDD9bL3gZcIkf1GldPsRIOzoBLSY/jAzhLM9kaoZDAXH2WBR0qANer6kJxxV3YG/YAjKRvenYCXGGtC0N49JhpY0ePHu2NTj3++OMK5tpKFEOntjo4Aa5rn87oRMFeOlimHSm/4YW9YX708OdR6j5xcIW1Ln/0LmXEQv6rVq1KtOecOLhxT1c5fvy4OnbsWCE8QnUX9vLxIQlJFFxhLSU8LinWW45ChySnCCUKLiU6jh6yDlrc4Ap7S31Z0nUM6zoxcJOa3B03uAAV1rRcW9ATAzepZRm8e8bdBoY1oT4V4Apr07Kgytao+cKHsRQmX7rF3BJhbtqWQhYzoKmfsLecRWymeUm42MEV1qZpEbMYq9xz3MtPYweXRdNJbj9w6NAhdfDgwXJxChRf2BvXwvFYwRXWJrlxSBK9Zb0k8OxhLGjT0yx0HSu4Lmz5kzS4wl5sEbXEBq6wNunNupIGF0CDbrNkWxhiA5fNwJJsa8UwvH7FOdwp+epnYa/tBml6GibXsYDL9n20M2ndINPEkLZhgmxtaJtHLOCmfWtbW6OahBf22mxKapKuHiZycLOwKbVusDCv2ag7qu2E0TNycGU7eTa9dkGYBLdv3z4XVPF+DMkPrrBRFBIpuMJatql3RVzoLeu2iGILf0k/UnD5oYRrvy51DVzZxt/k5xsCmuk5MnCFta79fMk1cAEKG0XR9kYGrqu/TeNff679q0/YW2w+tSlb9XCRgCus5fdrFTGzgOlPr8xS+y9UJOBm8UfDNkYNElbYW+p3dTZphw6usDZLPxm2MWg5Ycv5PWy+fEMHl7WsrvWQ9QffuXOn2rFjh+7kzLWw13Q9cCnFQwX3/PnzXq9v3bp1pfKNzZ/V8SwPEXn22WdVr1695Nbzs93/oi5yBBfYjp4ztixXQgWXXWCiZi1rdxhlEunRo0fO5iQsntb9udfnDLdo0UI1b95cont+7FojQlgWgokw9ksa/kP8wz4Le4P8lt2vS2jgUtIaN27s7d3kz8TmHhbpTGKFnb7KTrYPkjQBQw8PsPo+FtzrzPW/5+Knx/ffs4VCx44dJTuF0XET8etD4dPzk3A2Z5aLYsty2RsauDU1NapDhw7qzp07Ns/hraLTmYXhdCb5mWqVeJ7A27dvV19//XUen/xO6KYXLn8ov35+sFkKqtck/vj57rEhtiz2+/V88fxuoYArrF2/fr0//Xr3PKhe5TAbX2dCvQgJOwCuXvhs1aFg6OAOGjQop6YolB62LJe9oYBbXV1dkLVUeXrvjweNCsxffvlFmRz//PNPIZvWcwccFmCzup6DNl4Hq16EEg48uzQDNB8wO181LuzFtkGlbHCFtRs3bqzTQVeWB2HbH70drAsY4gXp9+vXT7HVUanDBlzSBUzOPAsspnNFdVyuYCfdNuSh227Dhg1lsbdscCdOnFiPtfQ2bfaQKNdIxMcw/D61lGzZskXpBbFU+Hz+NCt6vyBfmCBuNFH6bjrC3qqqqiDJlfexXliLUnpVJdVOII0CRjIF199bDpId7I0CXHTRmUvtgG2Dtr1lMZcdUKVXF9XDmho/TnBph6PqN+jPS5XN4m1sTA1pK4HBZesBStTmzZsjb09NHioqcDEwSz4Z6WJaLB0qmh3yi0uwMba23e4hMLisiOchbd9rozKIKbh79uxRu3btMlaDqhGWUjNxppqME1gUxcb33nuvat26tbHeBAwE7pkzZ1TDhg29XqlVbhEGNgU3QhUiTZo3gHvuuUdhe1MJBC47jT/11FPOsJaHzTq40nMeP368Kbb2zGXGAKy1GcIz1qaMgFkHF9Ns3brVs73pchhr5vbs2TPnq0oZeIQaFXBN9rrgVYhPai1btvQO1i/p8tdff9X5EUZ/7yQc2ytJXM5PPvmkHl1dvnw5x79Tp045/uz3rMfv0qVLjj+vQrr/M888k+NP2/v888/nuBW6sQYXA7Zv315du3atUJrOu7NOh5V2HP71S1R/4sfZP+ca8HV//zwxtibS/f2DOX/88UeOP6NQurAaUo9PT1nk+vXrqk2bNoptJ0zEGtyff/7ZG3774YcfTNKvhAnRAgwUMfQJBiZiDS6JPv3000ZVoIkClTDmFqDWxPamEghc9pR49NFHcz7dmWZYCRfMAnwdYpYLX71MJRC4JM5iKtbcjhw5Ul28eNE0v0o4SwtgW37ojK318XuTZAKDS+Lff/+9euSRR7weo2vLRkwe3vUw2JTeODYOMmOzLHAxzokTJ7zqmYa+b9++6qeffnLdZs7rhw2xJTbl8yI2DiJlgyuZ0oPjX/Ao9OKLL6pNmzZ573ziXzkXtwDvx9gM22FDbGnaKy6UcmjgSga7d+9WEyZM8Aa5mzVrVgFaDJPnrAOKrfgwgO2wYRgSOriiFC/clERGhBhVQfkhQ4Yo/h3EOzIv63ebYJO9e/cqfoo1dOhQzybYBhthK/zDlMjA1ZU8ffq0Yuc0qponnnjCq3YaNWrkvbPxwZ9RmtraWj1KJq5PnTqlvvnmGzVt2jTVrVs376sOVS4fXah+sQm2iUpiAdev/G+//eaVVGZFdu3a1WM2D83QGuymZDO/mH0ar1y54o/u3D06ois6oztjv23btvUKcdOmTb3lK+z3+O233wbuHAV56ETAzaconQd2NaVEM/vh/vvv94wD6A899JBigP25555TLO9gvPfHH3+Mle3ULORJ3uiALuiEbujIgc7ozrs/Y9aHDx/O96ixuTkDbr4nvnDhgtdjZMYifwwbO3asN81FWCFGhR2s/+ELDlUeRqca7NOnjxo8eLA3CMA3aGoKGMTBNW4MEBCGsMQhLmmQFmmStuTDmbyZaoMu6IRuFEx0dU2cBreYsf7++2/Fb2TooLAsc9u2bd50Wr6o8DcufmkDw1jmMm7cOK+9Z2Jb7969vYNr+gD4EYawxCEuafA1hzRJmzzIizzTJKkFN01GTkrXCrhJWT6GfCvgxmDkpLKogJuU5WPItwJuDEZOKosKuElZPoZ8K+DGYOSksqiAm5TlY8i3Am4MRk4qi38Bjg5uLShMIUoAAAAASUVORK5CYII=[/img]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAHcAAAB0CAYAAAC/ra0kAAANwklEQVR4Ae2dB0wUTRTH7R0L2Mtnw94TNBoVFSugsRvsBTWKGrHG2A32gmJFlFiwYNeoJPaKYAl2BEusiF1jj+19+c+XIcN+J7d3t3vsLjvJZXdvd2fmvd+0nfYykekMq4FMhpXMFIxMuAZOBCZcE66BNWBg0cyca8I1sAYMLJrucu6HDx/o7NmztGbNGpoxYwaNGzeORowYQf7+/tS7d2/q2rUr+fr6UsuWLcnLy4t8fHyoS5cu1KtXLxo0aBAFBATQ2LFjafLkyRQSEkLHjx+n5ORkQyLWNNzLly/TunXraMyYMdSqVSsqUaIEZcqUif3Kli1LLVq0IG9vb+rcuTP17NmTBg4cmAre1KlTU8EHYIAGcICvVKlSin9ubm7k6elJo0aNolWrVlF0dLTugWsK7o0bN2jZsmXUsWNHKliwIFN8sWLFWC4cPXo0Ax0TE0OfP39WTPHfv3+nuLg42rx5M02YMIElljJlyrCw8+TJQ23atKH58+fTpUuX6NevX4qF6wyP0h1uREQEde/enQoXLswUWrRoUfLz86O1a9fS48ePnaEDi2G8evWKtm7dSkOGDCEOO3/+/NS+fXuWsz99+mTxPS39mS5wHzx4QOPHj6ciRYowoCgmg4OD6fr161rSTaq4JCYmUmhoKEuIuXLloty5c7N6/tq1a6me09KF0+CiSNu1axerOzNnzkweHh60YsUKevfunZb0ISsuqBY2bdrE6nzI0qBBAwoPD6evX7/Ket9ZDzkF7oEDB8jd3Z01iFCvIRcYxT158oSCgoKYfCiJ1q9fT3/+/NGEeKrCvXv3LmsMFShQgJYsWUI/f/7UhNBqRQJ1dKlSpahOnToUGxurVjCy/VUF7sePHykwMJBy5sxJgwcPptevX8uOkN4f/PLlC02ZMoVQL+O7+/nz5+kmkuJw79+/T/gGbdy4MWm5saG2xh89esS+v1FqXbhwQe3gLPqvKFx0Ori6urLvRYuhZcA/w8LCWC6OiopyuvSKwT127BgTYvXq1U4XQusB7tmzh1VRaFE70ykCNz4+nn337dy505lx11VYJ0+eJBcXF9aX7ayIOwz39+/frHU4Z84cZ8VZt+Hs2LGDtaad1bvlMNx58+ZRlSpVDP+Zo1SKwkAHujSd4RyCi5Zxjhw50q016AwFKR0GOj3wiXju3Dmlvf6ffw7BxfBYvXr1/uep+UfaGsBACQYg1HYOwUWf6siRI9WOo+H8x7AmRsHUdnbD/fHjB2XPnp22b9+udhwN5z/6AzDpANWams5uuOg7RQSTkpLUjJ8h/cYXBoYMt2zZoqp8dsPF7ATARQPBdLZrAEOFmO+lprMbbmRkJIOL4TzT2aYBjJYhY6jdXrEb7r59+1gEZ86caZtk5tOsnYKcO3v2bFW14TBcTGYznW0awIQFfOuq3avnMFyMW6rd6rNNddp+GtOKMGMDszo1DxfzgOvXr09oAZrOugYwv7pWrVqsy1bzcJ8+fUqY37tgwQLrkmXwJ/bv38/aKfjORX+85uFiViMGD7Jmzar6d5ue0wbGu5EJsOwFTjdwUSQPHz6cpUq1W4B6BIzOCiT+tm3bEuZY6QouV/jixYsJTXwsuDLr4P+0MnfuXJboMcwn6kQ3OZfDxRH1Cpr5mN555coV8VaGOkdHRbNmzShLliyERC91uoQLIRISEtgqOuTi/v3708uXL6WyGfYaqxGwVAaDKrVr16aLFy9alFW3cLk0WD5SunRpwgKqjDApHSsFscwUKxSxVEYshrlO+FH3cCEIGhCTJk1iMzYwGx8Lpp89e8Zl1P3x/fv3LOFWrVqVtTdQUmGFoDVnCLhcSPRiYY1tvnz5WAMD3ZYHDx7kt3V3xOr+Pn36MFkwCICF37a0MQwFl9PDSriNGzdSw4YNmWKwHrdfv36EmYHYEkGrDvFGYsQn3z///MPiXr16dbZY3J54GxKuCO/27dtsmwPUyUj92bJlY1sXoLfr5s2b4qPpco4lIag727VrxybcI47oS0eOdXSCm+HhisTOnDnDlkK2bt2a8ubNy2BjRTv2u5g4cSJb+IxenocPH4qvKXKONsDp06fZGlss4urRowehDgVM/Jo0aULTpk0jhK/UGtwMBVdKCYunFi5cyDpEmjdvnrJ1AVc4NivBJiiYzYCVhPj8QO8YNivBUsrDhw/TkSNH2Ngpdr5BFykSydChQxk87HWBYhU5kftZvHhxBrJv374soQG4Wi5Dw/2bUu/cucPALV++nLBbzbBhw9geGig6kcOQ4wCJQ8PwGhICRq5QKmBaKXqLMKaKzzN0umCjFaVy5N/iLf3fhCvViIGuTbgGgikVxYQr1YiBrk24BoIpFcWEK9WIga5NuAaCKRXFhCvViIGu5cJFpw2+t/HDIIUtzuGprXrb7NIW5aj5rBy4GzZsYMOHGPTHDzvj4D+5zoQrV1MKP2cNLnIpes6uXr2aEjKHnfKHlRMTrhUFqXXbGtxTp04xuGL4KKIBXK6T/6TER75WyCyWJYqReWkNLrzBZm3iWixMBEDxLNeZcOVqSuHn5MBFkYyJhhg4wQ8THGxpVJlwFYYm1zs5cFE0lytXjk0yRC6uW7duqjrYWlgmXGsaUum+Nbi8fhUbVEuXLmUtZrlj2iZcleBZ89YaXEwktFS/opgGZDnOhCtHSyo8IwcuimGpQ/GMxqwcZ8KVoyUVnrEGF0UvOi0GDBiQ0kPVqVMn1sCS26gy4aoATo6X1uDCDwDGdGDeQ4WiWi5YvG/ClUNChWfkwHU0WBOuoxq0830Trp2K08NrJlw9ULIzjiZcOxWnh9dMuHqgZGccTbhWFIfZCWJXHEZQpNfon+UO98VrNVcU8DD/dszwcPFNJ8LCqIjY9YauOHz7cYfvQREersWZC7gW+2oxNio+j04CMTzurxrHDAcXihWVDxj4iOcOoEQY/H97jwhL7BQQ4eMeVsiL8bE3HEvvZQi4Yk6RDkbjnqh8S0pS6z+EK5YSSFSArZQzPFwoT1SYCFopJSrlD+ImFvE4F0sVW8MxHFwoCDMKeG7EtRaBIn589oN4FItowBXre/GeHNCGgwuh0SjSIlARCIpgNLYAT/ylFW+UQGIxLvpn6dwQcAETdameHOBi3NQWB/C8RMLRWsPPEHAhpDVBbVGiM55FfNFyttehyMZYLIdtyR9dwoVAmEGgN6AiABTFkAGdHvhh9X1aoMR3+bn4vHjO7+sSLiKPVmRa9RMXUKtHnnMBGVUKimjMQrS10QT5oAfUx9LEriu4eoYpJ5Gh7YCfPU78hOLv6wYuih2kTktCcGH0fkTOs2Upx9/k5blfN3AhiNFzLhIu+rIdcbzTBplBV3AdEVpr70rrRyRc1Lmogx11usq5ENpouRaNKBTBaDFDPt6h4ShY8X1d5Nzp06eLcTbMORIscrA0FyshICaV4ztYF9ZJlBA4I/mBBFOoUCETrlGha7pYDgoKYnWRXhZfnzhxgiIiIlJ+UrsLUVFRKffwnHQP5b1796a6//3791TpDkaiRf/Fmz9//kx1D+YBNA0Xu6CisfH27VtRDs2ew0Z8jhw5Un7S/ZKxubd4HxuIis7d3T3V/devX4u32Xe++L54E6YAxHslS5YkmITHxqRqOrtXHAAqWpHpOclMTcWo6TdKDehOmsCUDtNuuIgIUmBwcLDScTK8f4cOHWJw1d4G2CG43t7ehI2nTWebBmbNmsX2gLbtLdufdgguGgawNpKcnGx7yBn0DeRWtFVgBk5t5xBcRA4NEdghMJ08DWCHdlg3+fHjh7wXHHjKYbhxcXHMWBIGtE2XtgZu3brFrHHu3r077QcVuuswXMQDBiRcXFzo/PnzCkXLeN7cu3ePGeHw9PR0mnCKwIVxQlj7gPVNWAQxXWoNoHRzc3OjGjVqyDIFl/pt+68UgYvg0Qvj5+fHDD+ht8Z0/2ng5MmTzE5So0aN6OPHj05Vi2JwEes/f/7QyJEj2TccTLjJMVjoVGmdGNinT59o3LhxLLFjeo60u9IZUVEULo/wgQMHWIsQU29WrlyZpqlR/o6RjpGRkQSLo66urhQWFsYSfXrIpwpcCPLt2zdmgcuakeD0EFqtMGFp1MvLi5VcGPB/8+aNWkHJ8lc1uDz0+Ph4atq0KRMYNvJQBxnNwaIYzMihv7hy5coEu4RacKrD5UJiglm1atWYAsqXL8/suFuarM2f1/oRPU2hoaHk4eHBZIKF70WLFmkq2k6Dy6WOiYlhW97lzp2bfTopYa6U++2MI8zCwoYuzMLCJCxW42MsGI1JrTmnw+UKwGA4jC3WrFmTpXw0QAA6PDxcUxPuMDy3bds21lFTsWJFFlesQMBkBemAP5dNK8d0gysqIDExkWAGtVu3buxjH3UXbOf6+/tTSEgIs7qZkJAgvqLK+YMHD+jo0aO0evVqZrSZ29DF4IiPjw+z2smnpqoSAYU91QRcqUxQIMyf+vr6UoUKFVhuAXD8kGvQIoWZVOQeWKbesmULYYwU3Z8oNpOSkgizH+AwYoVZFagOUHwiFwIeZh4GBARQ27ZtiedIHgYSFmzzwh5vdHS0NHq6udYkXEvaQ66C5WnkcIysdOnShdDrI7WXywH97Sja0+3QoQMFBgay6gHgnVE6WJJNrf90A1euAl68eMEgxcbGslwnzcly/THCc4aDawQoSslgwlVKkxr0x4SrQShKRcmEq5QmNejPv6XkOCOg3+XiAAAAAElFTkSuQmCC[/img]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAJYAAACLCAYAAACDSWCnAAAgAElEQVR4Ae3dBbAtR9EH8ODu7i7BNbi7BIcQ5OHuhBBcQuEQPLgED8EtwR0CAYK7u7vbfvWbL31r3tzds7vn7D27574zVVtroz3/nenp7undrdqG4X//+99Kt2rV64/4u610D3So/NQ6Ka9Pft2hKSsVZdsDK++Nuo6se5anieuu8SL+rPOQec0qZ8x3kwDWf//73+o///lPOtqIHnH//e9/b6TxzP2sIP+I51r8yMPzWSHSRh3b0kUbnKOsSBvnpjIj7az6rMK70YH1z3/+s/rKV75SfeITn0jHT3/606qJuH/961+rI444ovrkJz9ZHX744dWnPvWpdMS9903hRz/6UfXxj398p3TyUO53v/vdxjKB6Mgjj0zxxC/L/cMf/rBTkXndf/WrX6V06pmnVY+vfvWr1b/+9a+dys3T7pTpCt6MDqzDDjusOsc5zlGd8IQnrI5//ONXD3rQgxrJ+JnPfKY65SlPWZ34xCfedHj+5S9/uTHtfvvtV53gBCdI6U50ohNtnJW51157Nab7yU9+Up31rGdN9ZMuP9TjAx/4wAY4SmC84AUvSG3Ky5NGPS5zmctU73znO6tf//rXjWWv8otRgWU6uMY1rlHttttu1bGPfewEmnvf+96N9DS6nOpUp0rxACmOU5ziFNVpTnOa6otf/GJjWsASL9I4u3fc9KY3rU0HKN///verM53pTDuly/N43/veV5vWwxe+8IWbyjzZyU5WHe1oR6uOdaxjVcc5znGqAw88MKUvQdmY6Yq8WDqwcgKaCi55yUsmYF3qUpeqXvva16Ypool2f/zjH6u3ve1t1SGHHFK98Y1v3Ol4y1veUnnfFExnBx988E5p5PGGN7yh+vSnP92UrPrHP/6RRpa6Mj375S9/2ZjWFCtOpHV+znOek0ZLH5Pj0pe+dPWnP/2pMY9VfbFUYOWgQjDAAigEvte97rWqNOxV79e97nXV0Y9+9NRm7T7GMY6RwF1mUtKqfD/1+6UCqyQGxvg617lOddKTnrR6wAMeUL7edvfae93rXncDVDFqXf3qV6/+9re/pfbmgMqvV40YowILsT72sY9Vz372s6vPfvazq0a73vX90pe+lD6iAFSc8VqHHnpo4yKgd0ETSDA6sNBglb/MLn2ofY7HP/7xabSyEj3mMY+ZrmNavNGNblQRvWwXWkwCWF06Z9XjkLFd4hKXSCvCy13uctXZzna2dG2FCVxEEORd2yWMCqzt8nV2AcMHP/jBjVHq/Oc/f3Xa0542AeuqV71qdcYznjGNXne4wx1aNQhdyppCnFGBNQUCLKMOPqB73vOeCTzkdXgqq0E81s1vfvPqvve9bwIZGdcsIe8y6jpUGZME1nYbyci6zn72sycgXfayl01gInQFLCMWGRtQub/Pfe6TdJpDdfBY+YwOrL///e9JsEkQuV3Dq1/96jQiYdjf8Y53pOkOgADpAhe4QGLYb3vb26Z7GoTvfOc7taRYpQ9uVGAh1Otf//rqkY98ZFpuo+YqEa+294uHrBlucIMbJNDgrUJpvf/++6dnmHgyLOoq+lJge8xjHtNIh1Whz6jAInmPldJd73rXoktW8zY6Ps7f/va3q5Of/OQJMA972MM2APPc5z43PcPE//jHP06j2A1veMMNsP3sZz9bTQIcVeulAQuhg9hBMZLoPfbYIxFzlVU60a44R/ucn/nMZ6b2ESfQSfqYTPsxPZ7kJCepvv71r6ckhKQYe6PWM57xjE30yvOd+vXSgFVHCALB0BXOsmqoSzvVZzm4gOjyl798AsoVr3jFBCg8FsU34JBfWSWy1ZIO4DDzrB8ufOELV7/5zW9WFlxLBVZOdMAwYgWwVnnEagI5A8TjHe94CSjMY/BS5z73uZOoAdCCp8pNb4AOkw9cr3jFK5qynvzzpQKrpEZu3UDOs4qh/FiiDZ4zWjStsSH7wQ9+kFa/RiR81T3ucY8NEQPznciH6c/FLnaxlG6VTWqWCqwgXhDfVEiu4wtdVWBFW8rzb3/72+o85zlPGnn23nvv9Fr7mUhT3Xzuc59LCmkjE4PACOIY3QhQ0YUNV1Mo6dkUb4znSwVWXQP33XffBK6wpKyLs4rPGCQCh+PNb37zpib8+c9/TiOXEY1yOg8Equc973nTqNVkUpPHn+L16MAiIGX3vZ0EpHjHW93qVgkY7PmNXmXAbwV4HvjAB5avqyc96UmJuWfC/N73vnfT+6k/GB1YCDTlIX2eDsRP4aOMRve73/02smDjj690zlfEO3bs2IgT9CDbOstZzpLyYJMv3SqFSQBrlQg2q67xgTztaU9LgLA7J7en/8IXvpDs+j/60Y+mbK5//euneKxKI22e/xOe8IQ0lZKBWTmKE0ceb4rXa2AN3Ct/+ctfNmRXVoCm+ADN/e9//yS3sjOJqif0g1Z/ESevzve+97209czId7Ob3Wyl2IXJACsIG+ecwKt0bTQ67nGPm/gjaps8UOnguW55y1umx6GIvuAFL1jVbbZFiwc/+MFpZUlCv0qGgJMAVtN287xTVuEaEIxKRhg8lu1fefjGN76RlO4f/vCH0whF+S4uRbRd03XBLvHTne50CVx3u9vdVsYQcHRgGe5p9jGrqx6s/mKlR3Zlups1Aoce8dSnPnX1wx/+sLb5PjrCVAAkaJ21Kbc2g5EejgoshL/73e+eOuOJT3ziSCQYrti3vvWtidkmIiBNj9AErle96lUJMJjzr33taxF905lrATu2gWufffZpBGxTOZsyXMKDUYFlCX3xi188Eewud7nLpuZOiVCbKlc8ILu6zW1uk9pi1Jq1QzqSvvvd707xCVHz1WO8j7MP8Na3vnWKy/K0nGIj3pTOSwUWoORgyXWFuRI6jzMlYs2qi84O2VXd5ls6QPbsTGRCGIwZByojUZsQ9CMf+UjaySMuSX0TXzoV2i0VWGXH5MAqdYVTIVBZ56b75z3veQkgprWQU+VxAYefimte85rVt771rfSKEWDYX7GknRUIVMm96BaNiFPnSUcF1nYxm6GWIrMymnBP5L78MJjAYL4x6rETh5VobKLgLKQt0DmGGY7d42UZ0ntW97wt76HfjwosX2FYkGLiVzVgrknZjSYHHHBAbcdyIfDwhz+8euxjH1v9/ve/T021iuR7CyDZubcFwld2XOIzrZnlW2tscC0VWGVjMaXsvDGkD3nIQ9roOsn32kTwqbOt3MLMuEtlCUVZikrb1YLWyBf7El/+8pfXFlPSuTbSFj9cKrDq2oL3YI/E2nIVw+9+97vqQhe6UALHnnvu2chU17UNj3mFK1whpWUN0SUwV7YBBRiZPU/Vt9bowOpCzCnHITJgt251N48p8fWud70Ekmtf+9qdm0lVxAiQvIzd1xTDXMCy1MUnkJpTOXDP47DKaVoGT7Hxi9bJVM7fgtGDWuYXv/hFbZZoglak6+UIE7Ivo4/8uoSf//znGxJ+rIQpdQrTX1733sAyFFPBMA0htEMQ2nmbIm5yk5tsMKZ5IfNcT4lQTXUBlNgqT+3SFFiL3vGOd0wg5Aw3D6GIxmuJ1xaiLmRZFgvEGxyOTC10AlY0hgdhDSJHscOEpv4iF7lIWtmR0djpO2ulkjc+8mx7lr+f2vVLX/rS1LmsGfKdNmU9jTCEp6ZMnpTzYDVoxGPU15V20hPIWlEClw+ciGNKoROwVBiTyiuKvXAadKc73Slp6k2BLCZ5F+adL1weTqmRQ9Sl/BCISoI/opaydb6ME+USK9jpjbnn4z0P+CXA4ierSRGdx3cd5dgFBFhcbU7NpKYTsPAIvjQM4+lPf/rKMjfUEnmjo8H5s7ZrHYRHsEJapcAalM92oHjc4x630dl5G4Iezj44HyehcB44u5UHEcI3v/nN/FXrNf6WwFV6JjVTomEnYPlbhOnPKiR2lATRWls/IwLAEjdYTdkNvEoBmHSo0SJMWeahiSlUPo5Zimi0KfNHvzvf+c4pLS81Zo+phE7AeslLXpIq31VrP6txOXF8vZh/S/WQvOfvZ+Uz5jsru5Al8fps1G0LTe36/Oc/n6YzwOK7oWuI/EyB4XSEtWnXlWXXcuaN1wosDbjFLW6RgMUCIRrkbOh1xLO+lQCsUOnk1g1981l2/A996EMb0u8Xv/jFrcVTxRDP1LEPFNKYf8DiKKRvQH+mzngtvO9UTGpagYX/4W9Aw/05AnHIq3wphIMOQ7gdvn3nePFn+W6YF7B9O6dL/KiL6cdHoCP5DtXuPES8/BkDQE5A3v/+9298hBFPetMY+rIonScQYRA7yAOrEnnPk9dQaVqBRcRAwYq/8qXSsNvnZvu4LwRxAc+qhzylz7I3BxZd2RQI0kZYQtBw+0g42lZnQLzKVa6SOt3IXzLvbN2JbYCCDbzQlmdZRx8/yb08dt9992oKvrVagYUHsBq0AqIoBqiLXvSiFZtumzFvd7vbJVkWcw6Nes973tNZ+p4DK6bCvkQtibzV90ZtPCGZFJdEZX3L+5DOcwnJuiFCxAMKskCgKG3SIm6XM1PoMKlhghP5d0m7FXFagWVHSRDyDGc4Q/o1iX/tmRJVHuPKJIQ7RDIuPFPdlvK6yvt62S8hagCrLt6Yz/IO8iHQLqgvoIT5S1v98D1kfFiIMgBeKKJ9rHl5Zdy6e/EdFhRhUgOoNCRjhlZgmd4ACzFvf/vb1zKgGmCpS8iH98B3dQmmCatB6oynPvWpXZKMFkfnMYmJTQ0xbQ1RIYJWdGvaEd21DPLFUIjbqDFmaAWWLy1GLHbXs8LVrna1BEBbw7sEnYV5NeLlClzPpxiA3weG52Tc1zdoV13bQhHNpZNRcd5glIrNKVe+8pU76R7nLastXSuwuIb27xerjjCpbcp0x44d6ctbxGivjvBN5S3zOT2eHcuAVeeko6negELcMEu+xJWTfMkJS+uHPm1UB7wW8YXFVu53q08+Q8RtBZaGhntDv5qNUEfI8PrL/HZVQ127tMWPNqldLGRe85rX1DavLi3VD3rQCTbxZFwWARaxQ1f+tLYCR+l0g9didTIWr9UKLHwQUYKGO9cJ+TTSF33Oc54zjVhWTtspWGQYjdHAqrjPcp7WgiXILHstQlZ5i7fo7hvgftnLXpY+ACNXLnStA/5W9VMrsBRMn4Vp5UOA89VSFkN2ZROBhpz5zGdORm1bVeEx8rWqix8p9f0lydvf/vbqWte6VvIW0/RrYaMhYJm+2tiNLu3Hr4YIg0fA+GlBl7RDxekELLIWMisrDrtDnv/85yfzDytBUt+nPOUp1bnOda7Eh1HOzuInyornX1F+XcYb855lh1UbXrPNqK5sAwEoe37MfhNdLIrkT1wTDkMWbS9DTIsuo2CYL5d1W7SMWek7AUsGmHiadGYz5FlWgJhY87n9ciwpSc/7DOUayvTDiFgn45lV8aHetRHbaMyflRGFzK1p1JFPU16z3mkHR7dGK2XU+Svt09aoA/s4iwF5+snmsu3kOgNL49htY0I5DAMsoHLGf1iBlIZq0cgmwuDfuP3xY0i6tCmGI444YuN3uyFGaWtX3o4ucdlh8X8FBF2U2nn++XVelmuLBiOhvEuT6DzdVlz3ApYKkLQbvWwjV1lngGuTv+SNjobg1cK6gaHaFMOjHvWo1OF4zLC7Grqe9LFmAcCyQhwqEOjS58qX6k0f6Ye6vhiqzMinFViLVCJPm19H4RoawJqKSifq6Uw8QC+qY6is+ijYtZGohlyJdUMuAI72x1k5YUHCpmqogL4clKg/dqXNkHCocuXTCqwhCyvz0vApm81QqFvpkl3Ns2fQCo9O0QqtzlFI0AMdAsD42CEDIwLmy6ZEH2/TAmLIMuU1OrAI8aLRMVoM3ch58sP/mZ7VjQyK6qlv/fBndt+Y5qjGmoJ8r3SlK6WRxYJoyIB1ib2PRCYMCJYRRgeWbWOG6jBNXkaju5RhdQtQ6kYwPM+XzvkaYSVxRZsjthvf+MapLIuhCH2BHOnKs9EyvNow3Rkq37Kc/H5UYOksS2Ff9SL6xbxBQ10fdNBBaQqkxjnssMM2OiM6Jc5t5Rn5uoCSR0MgpkTuYkPfVm68V0+iBj81N/qSN4b5ctc2RF59zqMCS8PwMZbYU3IKomND76mjbdvqEsqOKu8jj7rnPizAYk26FTInpkwEvPhFAu26OkT9hjiPCqxogK96KgHBw7ZMR8+rUO/bcSTlRhSrt0UV0XW0tEKNDbbs3/roO+vya3s2CWD17YS2Ri36ngdnnWzPIKl411C2Q1rqmi7aCLwYIBNm2lk+ZIh6velNb9pY5S4iiO1St0kAq0tFlxXHl83gTidjpPvKrqKe+Cp8ExeSpb+GiJOfybqAmXiDqc1WBPKyMAWn7ejjK6JvfdbAKihmJxKjRgphDmvnDQBpMy5rUx7/2oJyKY1DEd0Wf973QE4vCcBbad40CWDFUB3EKu/j+Vaf8XqsOIxWZE+xepqnXHZrpjfeZFgsCLPaReZlBarssEaYp9y2NDzfhAdCyvVcqV7Wr7xvyzt/PzqwrMCY7pI+jx0QPVQrXAMtuqjQNlNrl7bZER2ypnmk/H1oZ6FgZDQy28K2FWFUYPkimPk++tGPTrKirWhgnzz5WmdzZuTA8wwZ2r5+oA5F9FZYeuTlG4m32qRmVGBhcA3HvhzmM2XIiVG+i/uIE+fyedy3nY0q4aOCfq/pb1xt+dS9L+tWF4fsKnZEP+IRj6iLMtgz9fExx8p3lrpp3kJHBZbODCX0IruA5218ns4v32xmQOwhLAxM7ywaupoFm3bDNfcst5N5nee9BiwmNfFrYKvXLtN1n/ImB6wuX3fZwHnSlHk8/elPT4yzVVzpda+M2+WerTsPiKa1JhVNWe/w8bDXXnt1KWKhOGYLCxUfkg/K3k4h6uQc1/MUNBlgkRlZRc1z8AWKVys9v3QlCJt+29wRmZWB0WbRYNMF9QmZWNPOprIMv+dVB7RYpFPLfJvurUTDpAYr0kWn2ZRX+XxpwKojVD4V4i8QlrLUuc/B1ISVxIte9KKyfY33eX24ZDJSWSnNwzjneUWBtn3x87Dffvt1Xl2y8AAstlmmxrp8I/8u56b08RzguU0g4rBnYdY/E7uUl8cZFVhMk0PK7c9WNsQ63vWud+10juezzkaaWXxaEDNvfFyHAtiUgNcSZsWPdHXnSEeqTefI/slIyt1muW3OPbNk73Uypl0nc5NkFLWA8K5OCY538w4fF2XGmXDWO0c5DYtDT+gdUQiTGh4BAZogt6xjXRu7PFsasOoq46vkKIzZb9N/YerS1T3j/6AJWEHwMp3nABACQ6vCoZlY5sCYY1NNudJUNkadvZfdStwP6WD7NwHmyU9+cvJOHXKtvB32Isr3oQ996E51FsfI4x1DxVLIy5e8D4mlKnMgq9Hg7ah5mnZrl7Rrux8VWIjgS2Y+22YI19YQ/6KZZzWFySa7ouZo+2dgWx28zzvfffiCJ/y0CSUPNqEo2yhFUBkelCm/jZxUQoBmI0QZAMo7myWCh4uyw2EuFZGfPeQBnVmSShvyQ3tF1UE5RrEhwqjAGqIBkUcdsILQEac8mybCEx4eLVdvlHFn3SvHtGcqM7UJUbap8FnPelba5Fvm7947h5GFzZQOBzZ8n13n/kvIZq0MVq5cS1rslEy3bXjSyTc3j1EnIHzlK1+ZeCsjNZDhLQH0kEMOKYuZ+35bAavOvDk6uI5CtnOFGiXcjNfFa3tGas6KgX8wu2LyjgZe/JCRoFQRuffOgbcBFitJ4OKm3OrU1FRn+IePinzL+ilfOu/zuognnT2ghMCxSZadlmlxqGlQOdsGWHR7fadCYNKJbKCMOPMGHW/ENNIAFpA0Abp8nt8zl6GFMC0tMnrkeeZtsjsar2dxAMA+BPyWaXdo3nJSwGoiSE6cputyKmzKK56bhmIjB6cd5eqpqZy65/IECiYpOi/KqIs765kpLHy2D2mIZ2RkMeF/1LHjml3WwQcf3LjfURvmbYc2TgpYs4je9q4EVlt8rrHZJBkd8k5sI6ZVlQ4ppw2jVMlDtdUh3keZ0vuZkzqxYh0iYNaZV9tEYepj9271fOSRR9ZOsUOUKY9RgYWgpL+Y1D6/vK1rfB9gKRdxdSDBYFdT4PjZkqnENDqUzCfag/8BAPXyA6YAXLyfdY64cRaXcpmQNv63w6LBqEqGlceble+870YFFsbSXxVI3bv8bHtWI7sAK4iJ2Q6fBiTPOYMbcfKy4hmhZeze4RgFEIYIkT+g2sALWOo1bzCqkonZgR07uWk0CEMx9MsIowILIcO6YVHfDU3Aik7LiWm5jXk1NZDmR4i4cY7nccarsAYloSbQLFd5Ea8pfbyfdeY5GbBoItpCXTnEG4SjbLssTJx5ySHOKEfYuvRtZXZ9Pyqwcl1hk9S8a0O6AAshjU6x65gcp8lHJ9DY62iUyjuAHAjfkj9Tx/K+a73zePIgpAQsUvC60FSOdhGwYso5W5MHZTYBcF0bm/KpK3OeZ6MDK4b+rRqxSqLkvtqbNjmQOZFK+2MsQWM+VZb5DX0fNvfkTE0r1QBFnPGI++yzz4YYgWyOTRnVTkjl6+oZ6eveLfpsdGDFVMgb4CKhacQq8yStNkX4qpvc+uBR/C4upqQ6AWWZ77ydVKaL/yBaIJQrz7zMSEdar67UQOpr5zaHtvjIPET8/NlWXo8OrHB4Xyc179PwLsACEPo3HUDxivlG8JLopkG6O9MShjcfscq4ferYJa4tZ+pHEW311hRYPHDSxoszwaz/6PihOV+npm9hq+vaVDfPRwOWRmMm2VIhYjkt9SWKVQ+mdVagMiHZNmLlewb5Py2nHSAk7FTHvnWZVYe2dwwWActPsZrso4y0VtMh8yKiMGWbEmNBMVSdZ+Uz691SgVVWxD2JNT2V7U/xPs5tneB9xOUblSVBUxCPbEin6RCWBkYsSly2XKaPyKspj2U8Z4umjlat5VRNd0iYyxrBB0J5bCFis+usaXMZ9S7LWCqwysLdm2asDuNLq4vT5Rlbp7rVT6T13rSh03ztysRLUXMwL+GoF9PeBK6m55H/UGcrUaBST+YvEYyqdKH86BtxfRwWGD7IECMsq45Rp1nn0YE1q3JDvuPmmtwKiMLlNVAzMLSAYItVdtAYHWXVil8CLMZ86kAh7adLoefzEWhDaTg4JL0WzWtUYC2r44yGRimdRa2Rj2z0cywbSnlVEHZZdYzyWI7ir9TVCpGeL6wR2OUTR/BtOpTUP8rtcu5Di1GB1aUxi8QJQpguTB2mEACj8wMuh+v8Pp4v+8xM2UqPVWkw5dRO/GUBmT+PGV27uERahGZDpZ00sAIYizaWNUIYteks7ikd9H4ONvf5vWdlnIi7lWdlMrqLqdCHQJTA1syKdiiz4UXp2SX9pIHVpQFd4hAb2E7my7eS4ptBhzn3OSh0+8TvE1d9ok4Apa4+Ag48jGK5LK1Lm4eK4+NGP3/PMIoLXT74XQJYeCwSajtT7FwhjHWe6mHXDtEI8+Ry61eXTh0KVPLx9xELB9v0iDq6lr9LAAuBiBYIEPEoJNpTOliOqk+cXdsEMbS5cF/A2RhCU2ElbRT1+5euYZcBVh1BfH1jH3m98tEg6pW/34rrsswog+iF7wkWp+EFp88P1ndpYAUR1+fNFPAPIFYSFNyxDT9GrByMm1P+/5NdBlhBjDg3EWTZz9Unr1Pcx7M4L7NeGHX+I2zsoC6KHz2tR6yiF6Jz4ly8Xt8eRQH0oXw3QuGrjFAEsTuO+h92H4dwu8yINXX0dAV913jzttdmC5J//5IOmy4WKMQf6xFrXqqOkG6rgdKnSWy5qI/8njl3H0kovAZWH0rOGRcYckDk13NmOXoywk+iBQJkm01yaxMaAcBaT4Vb3E34EGYsfmnCUw6DvNisuoogU2cMOrUXY0nty9sRwMJz5c9nkXnNY82iTvGOVQHi8vRsymD56rDFirGgTawU2qsWmOCwnKDoJqSNAESOmArXI1ZQZoAzwtrpwgmaH2PqAELD853vfEnVwVCQKQ7jPEzvnnvu2egPYYDqDJJFPurQROy+++6pTYceemgCUv5egTFiMSzsGtYjVgdKkUKzgyLX4bSW/oxilqGdw7TI5tx708m+++7bIdfxoxAl+K0v0QJfqWzSfETs/x1xHSMWZ2/xrk0pvgZWx/6lN+MMjVIY0PKv2jW+xIYQTK7fpoQlQMfsR4l2+OGHb5josKM3+hIzmOpdO1yHTRjVjmd2OOVm03WVXwOrjio1z4AnTJdrXqdHsRHCHj/S66kHUnVTuz2WcdTdhw2+0Tjet/05bA2sAXo/Ri/b2Y1YpsTSqewAxQyehdGXaU4cRqG4dnbP3VN4tmZw6B4vlrugrKvYGlh1VJnzGTcBgLXHHntsqe+pOatXm4xpTtsRzDvJe8Ql54oPqi7jNbDqqNLzGVsvW/dNE6xGmUJvpxDAWq8Kt7BXrQJtbj3ooIPS5ob9998/Mbh+PsCJiE2zGPntFLhUMhJbFeZhPWLl1Fjwmj4NDxWHUQpzy2sOz4TbDVTIZaSyWvQxCbMAFeRdT4VBiY5n5s08D/OOw3beDh8uhwhHjVp77733wm4vO1ZladF4AbTfsc/Pq9bA6tk9mFarKb4SnO0HpAYxWvGcYycP9c6if9roWa3JRV8Da84uKacDUmr//ONIlrznwAMPnDPnaScr291U2zWwmigzx3MC1FhBkfnsymENrIF7PzYe2NG8K4c1sDr2fkwBca5L5p0/tVqaL+qsty7/VXq2BlaH3sI/hfvFWdG5HeJ3weZOzPyuHNbA6tD7fmJEq3/AAQdULALYMLEYBTgrQz6tvOMUzWglrue7clgDq0PvAw6HHawWuBhiGOc3cjZz8qvun3/eGalIqeP3vx2y3rZR1sDq0LUEg5zO2l9HwQxIfslGtODwIwKCUXHIr/KNCB2y35ZR1sDq0K2YctaW7NkZ/PEAaCNFHKxJGfaN4YrcEi4AAAA8SURBVGWvQ/VHibIGVgeyx0owzsxy4zA6rUeozURcA2szTdZPBqDAGlgDEHGdxWYKrIG1mSbrJwNQ4P8A9pcUxIanEJUAAAAASUVORK5CYII=[/img]
Answer the questions for each of the two solids shown.
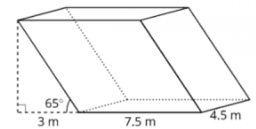
[table][tr][td]A[/td][td]B[/td][/tr][tr][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAGQAAACtCAYAAABGBdooAAAeSElEQVR4Ae3dBdAENxUH8OLu7u7u7i3a4lLcoUBx1xaXFi3Q4hRvseJO8eLu7u7uy/wy877Jl2/3Lru3d7fXITN3WYm+f/Ly8vKS3aX5v5sUBXaZVGkWKMx///vfFDv8BZJaa9QjDSCouOlgqMORCpC1Nu2RMj9SAKJn/P3vf2/+8Y9/jESW9SVzpADkpz/9afPIRz6y2W+//TYelCMFIK9//eubXXbZpTnWsY7VfOtb31pf8x4h540HBLvae++9EyBAOfjgg0cgy/qS2HhA/va3vzUXvOAFm6Me9ajNUY5ylOY2t7nN+qg5Qs4bD8hnP/vZxKrOd77zNac+9ambs571rM3vf//7EUizniQ2HpCnP/3piV098YlPbG52s5ul6w996EProeYIuW40IMaP3XffPbGrL3zhC80LX/jCBMi+++47AmnWk8RGA/Kzn/2sOfnJT96c5SxnaYwlX/rSl5qjH/3ozRWucIXmP//5z3ooumCuGw3Im9/85tQjbn/72zd//etf0+TQAH+CE5yg+fa3v70gadYTfaMBufe9750AeeYzn9nc8573bJ70pCdticCvfOUr10PRBXPdWECoSvSGE57whM373ve+5pjHPGZz0YtetHnjG9+YxN/b3va2C5JmPdE3FhDi7jGOcYzmqle9avP973+/Od7xjtdc/OIXb3784x83JzvZyXaIv5uiCd5YQA444IDErh73uMc1v/jFLxIgeojBPCSvj3zkI+tp5gvkulGARCvnX+9610us6YgjjmgoF49znOM0F7nIRRIpjCnUKI9+9KMXIM16om4UIEEiPeKUpzxlc8YznrH505/+1Pzwhz9Mou+uu+6agnz+85/fEn8DxIg7dX8jAXnb296Wesctb3nLRN9///vfaewAFGdOct7znjcN+N/97nenjsG28m0kIPe9730TS3rZy162rTJ5b7jHPe6RwrzqVa/aFmbqNxsHCHH3Qhe6UBozZq19HHbYYakXmTRukts4QOisLERd5jKXaf71r3910vonP/lJc5KTnKQ5+9nP3vzxj3/sDDe1FxsHyLOf/ezEih7+8Idvo6VxpNRfXeMa19iSxLYFnvDNRgGSzzE++MEPbpH1z3/+c/OWt7ylOfzww7eZAj3rWc9KgGyS9nejADHfOMUpTpHE3XwR6nvf+15z7GMfu7nwhS+8jY197nOfS7P5K17xituebyE5wYuNAkQvMOG71a1utY2URNvjHve4aWKIdYX7y1/+ksTfE53oRM13vvOdbb0nwkzN3yhAQrv7kpe8ZBsd6bIAoof885//3PYuDCBe8YpXbHs+1ZuNAURrJ+4e//jH37HWgWVRnQAk7yGIHuLv7W53ux2D/hRB2RhAqEOo2C996UunXpBPAn/wgx8kEde7UhQO7e/Zzna25g9/+EPCII87NVA2BhDaXWY+++yzzw4aIvQLXvCC5rWvfe2OXkAyu+Y1r5nW3TdB+7sRgCDq9a9//URUom1ft//++ydhgKp+6m4jAPn5z3+ebK5Of/rTN7/97W9baRpsKPw80Kc+9amk/b3KVa6yg6Xl4aZwvRGA0O4Sd/fcc88dNANAgBB+GYhAcK5znSsZPxAApuw2ApD73Oc+CZAXv/jFrbQMUMLPAwVIe+21V0oj1/7Guzz8uq8nDwjznotd7GJpJv6Nb3yjlV4kKxM/C1VtDuFf97rXpTGI+DtFIKLckwfki1/8YtLuXupSl9ra+1ESFBDnP//5mz322GPHPCQqKsyJT3zi5hznOMektb+TB+S5z31uYjUPechDgrY7fKoTKnlmQeU8JMDjs1Bh2fjRj350RxpTeTB5QG54wxsmVvPe9763k2YG6lyXFSDkETxjSEc4eMITnpC/mtT12gEpiZffWyM/7WlP25zmNKdpfv3rX3cSji4rVCdlDxEp0vz4xz+eeoieUqpYOhNf8Yu1AxL1DaLFPf/tb397mp3f+MY3zh9vuxYvegi7rACkLT0WKsYQ2l8gtoXZlvgabiYDSFvdH/CAByQW87znPS+97iLgL3/5y4b09NCHPnRby28Lf+c73zmlecghh7RlufZnkwGkJB5jhhB3v/zlL28RKsKFv/Wi8gIQdGKAmaKbDCCIkxP5K1/5Spp7YEOxxpG/z4mZP8+v8zBxTTPMQPvc5z53MrKL5+LNixthl+lPChAVDaIcdNBBibU88IEP3HqWvx9KFIP5la985eZoRztaY5DPXeSdP1v19eQAQQCEudGNbpTE3Xe+851bNKkhWE0YYi/xlxhcE36rACu4mCQgv/rVrxqaXbtqDdjhuohHPW9NhBRV4z72sY+lHnL1q189rZ90pVuT1thhJgnIu971rtSCTQpr3G9+85sGa3vKU56yY4GqLT7wbJ8+6UlPuqX/mgookwTkwQ9+cALkwAMPbKPnjmdUJySn85znPNvE3jJgTnRiMrZF6TglNzlArF0wVmDM0KXdLQkYE0P7Q0IiK8OU94AA4tS0v5MBJFqvrWqM3tjumovUuBwQUlSkNSuumbqtb2buv/vd77bi1MSdle6i7yYDiIogBvNPrORhD3tYdd0AMkuXVSYkH8Cx/SX+fvjDHy6DrO1+UoAgUhgzzNLultRygMDlL3/5xgYeadS6Jz/5yQn8xz/+8VtR/t9DtkjRNIwZaHeJvETfWkehaGBng0UErnUmhmy9GD/kY886QZlUD3nrW9+aBtqb3vSmWzy9lrhDwpm3nPOc50wriQCdgpsUIPe73/0SC3n+85+/MtqE9ncqJz9MBpAwZrDy97WvfW0wIH3ZzWte85qkornjHe+Y8oz44Q8uyMCIkwGEMQNx9xKXuETaRdunPohn25qNO30d8TeMH8L2t28aY4afDCDPec5zEruiAunrENJZWWx7+0hZ8hGe9tcxHYwf1tUzos6TAARRaHfNCeix+jrzEGed5Eu4fdJg82vuk4u/feKPGXYSgDBmON3pTpeMGXLtbm1FSUh9JoZlunoG8fdqV7va1pp8GWZV95MAhDGDU0VrtbslcYwDYQYURg5lmFn3VCfEX9pfaa3TTQKQMGZgFDfEYVkEgjZDudr0HDCAbZG61unWDggFonOusBxnJg5xzEQdRMPeKmbqfQdnRti0v3e5y12GFGG0OGsHhEUJdsPCxKExQxwpi6mQ1h2A9E3HOBTGD+sUf9cKiFYcxgwOlOnbqhF9SJw2sHxZgU6L+FsaP7SFX9aztQGCkFpzGDMY2NftHvOYxyS2ZSl4XW5tgKgwETeMGWh6x2rtQ4gpbydis463TpJrf4ekNzTOWgExCTSQOq5vUTDEj99QYhB/bZ92OHPX5p+hadfGWysg9nwQNZ3www0FBf93rskiSsnI39cVlGldxg9rA4S4a1eU+YNDARZxFqZIaTe5yU22zbSHAOyUOr327ne/+yJFGhx3bYBozSxLWJiwNBlCvKi1/YWkowtc4ALbAIn3fXyn1BF/ff6i5uAzDcvEVKOy/Zpvtl9roFGWbW2AOHkBa3CgzKIulIvAHaI6yfM3mFufp9tC4NyVjQZgTtJmSkRjbOngSle6UmPW73mtJWWex8oBIerS7jruQqv+wAc+kJdn0LVJnT2GDqcZKh0FsfnxTRL7TcLl7z1zTztMALj1rW/dvPSlL218C8tJRb5j4njBIeLzygFRGV3aQWTMObtOZghC1Pi2GJzhDGdIrRTgQbyauG1hPvOZzyRVTtiGtaUXu7EcSIBl5u7rX/96c+YznzntDO6rfVg5ICqnO9Pualldqo42IuSVzq+pOsz4bcbpSi8PP+/aymMc9B+SW5QnfPbEPotBfxYu3rknsJzqVKeqGociPn/lgMg0ztTVzcdy2KDfWI6UZYxzekRO6Ehfy0d0PeGrX/1qPE6+5WgbVYdMMFcOiK5OGiLJfPOb39xWkfKmjRBlmGXdv+ENb0ji7y1ucYtWQJTtRS96UTryXJj3vOc9aTL5/ve/v2HGxPDbB2f6upUBEsQluZh7XO5ylxssGs6rZOQ1L9ys9879db68zyl1bcnGtgzcZzrTmVJ97nSnOzUO3FQ37LMcP2rKtTJAovJPe9rTEit41KMeFY9G8Wsq2ycj4vO1r33tJAlq9W3p0xAgPNAc2Mz63lICQJjCtongbenk5VopIAZclaTA81WcsVyoTkpevmj60Xh8Z7d06sK4ztyDPfLLX/7y5k1velPamm3BDSjlCXfzwJDHygBRmGADungXGygrXnNPU0xB6TtUba2yJo22MNir+Y2vvpUzb9KX2bxJ5Cc/+ckt6Y4Yb/whpekxfT9OtjJAVDjEXQeRRWsJPydIPAs/fxfX+buYGDoRiKTlXf4+4vT1CSA+e+Hkh3LzkBVKUliXpPjUpz41vddz2lxX+VYKiBasEqSTLtdVUOG73lGdxDLw0Jl6W3nkd7e73a2V8L7eoy7WUNrK5dBnSkqz/j5uZYCYbFFtEHd197ZKKDiCGhP45XXcY0v5BDAAaTu3t4YYXWURNz4NTi0f4fhaPkAe+9jH7pCmKEtZ0jD867sSujJAbFVjWUIdUYqDQTSgGUh919Ye8vLnuRNGfWMqH4OCZS1iBhRlKH1qGVvfLFzlah7qHxND0pVy2k9vJ9Y73vGOpONiBUNf19fwb2WAxIe6Zm1VU3haUyah1jfKH4mGOsKyLxDCAecOd7hD4xMWY87Wpa832s9OERofPdZD/LR+NgHKJcy1rnWt5F/ykpdsTBaHnBO8EkBU6rrXvW7qwma0Xc6WhEMPPTSJk+ykiJX5j0E2G15A5V9HkD62ZaFqGU4PwJ4YQeQOKNQkzpW3PY54zDc3KYWAPN6s65UAQtx1KoNunLMaBVOpNhetMH+votYpnvGMZ+yIEuHC3xFggQef+MQnUr7WOoxvbXloFERj/iJu6YAofEgc1gnywbhPwWl0aVap7FdtgKA3En/tI+k7r+hTR2GXDohM4tzd2KrW1sLygntfhsGvTdIsGpXv4j78PK2xrumpiLExr2jLK56FPyTv0QFRmLxAIe5aP3cGVv4uL3A8Dz9/RypjGU/Z12b/q9eRgLTktvh5WkOvmakaR7pOfoh8wx+az1IAyQtj0d+kjeRRqh/ycF3XKkhaMX9BDDy6rDStK5Mis+NgiWWYrvRrnxNzbVcg5rLfCpfnk1/H+77+6IDkBVDA2KrmQJnc1RbeZNCGTD3Mh8Da4iEWwIifiw6qeRldR37SNYYRKoaIs2W6XfdLA0RFtNYb3OAGSdw1cYrKdRWm7TkWhVWR8YnFbY7Iu8gOqrY0254xasC2lvnZi6UBokKOvLBVzS++U9tW0a5nALUJ1KSMKrvLBSC0q2P3kDxPW98IFra+6bnLcKMDkveC+Iiwc3eDt7dVQpw8XoQxGzd3sb6Qqy3iffjCYSVjGMpFmm0+0Tu2vuWagrawQ5+NDkgUBIHjZIahW9WcjUjUZPvbBljkZYaud5DE8h4yK07E7etT0ShT/tmLvmnMCr80QLQmZ1ExGKOgC1dLJAYQ9Faks1xNEunkPvbBFmpZrTbPK44fZEdc9vrauuXpldejAhIF4h9xxBGJ9w/9zNCDHvSg1BL79i55RznKyi56L904scipReW4OEbeowKSVziOYg2FXBAp/DxseY3t7Lfffonl+dxqjatJtyadeWFok62hW+t497vfPS947/cLA9JGCAQliQz9Voc0AeHXln5NLYfGq0k75lZ6cZtbJO+FAYkCRSH4xFCKuPxjjhFuiB9pD4m7jDi+6U6qM751LbYNzXc0QBQgCEdNThIhkazCEYmtcWu5+QJVlGfsMpigWi6mEhrb9GhUQKLicSjYskTDyCd8UhyJjElOLvbG+2X4ocF2CtGYbnRAbGLx5QGmM8teOwhCYJFxtEbeQ+L9MvxY42HH2+aG9s7RAclX15alXigJABDsw+RwFXkiNrWQXmlfSp8DO8uyl/ejA2JN2fiBp6/K0fbSMTEzWlUPMSm8znWus2UnMLRHlDQaFRD8254I4u4qDyeOw2eGTkJLotTex6HPsfVtDFBGBQRhqEpYg89SBtZWuCYcIpB6GG/TDgRRwq9JY1aYWenYG69n+o4744cx3GiAKDgrP+zKVrVZFRmj4GUaeueq2FXkzUKRhtni2bzNRxFnnj8aIDIKO1ib71cNyLyKLut92CuPJf6OBkhYitsIuSpxt43Iq24Ihx12WOIKN7/5zduK0/vZaIDEZybspViF6DmrpqsEhb7NFm97XsYYN0cDJPZDjL1VbRbh4x1rFoYHGkW5RhFhluUbu3bfffckWR5++OELZzMKIFokS2/i7hgnM/St1Y9+9KM0KWRQseqBXVlj65vGuGjvHAUQS6jRbZdprNYGFAKYGFKdjHHWSVse8545+YH2dwxd2sKAIIiBzckMBjb3i7aSeQQo31OdsIpfttVJmW/cs85k+1uz9z7idPkLAyLhEP0cvLIOl+uy8PRVNwh1jpMfwvZ3KB0WBmQZk6OayuREZ9ygh2qlAOlyeZyuMEOf23nLiM6keBG3MCDUB7FVbSz1Qd8KETcNqAcccMBMlrlMQAgWtr7ZLpHb/vaty8KA2DyjZdg9tMwKz6oYUZcFCGCiDOHPijfmOz0zJM1QrA4pw0KAEDHtraO/YmbJDSlEH8KU6ef3+XWZpnfxK9/F/az4EWaWH9pf+yjn5dWVTm9A8kLrpmHMMM+YrasANc8jz/DFya/zNOJ5+Pm7uO5653nXu4g7y7ffkPbXTuOh2oqFAHGUqsG0axPLrMIv410QM/y2PGa9awvf5xkLFItkxlSWlENcb0DyTPbaa680ftiFyi2rsm3pUpewItQSsU6bSZmvmhMYTxZRobTll9d71vW97nWvRBOHfA5xgwFRcYd0WQtYpk0tLbI97vYn5moRJ+84/OXVr351AuOyl71sEjkRxHPsg0Nchhf77rtv+qxrKRaPbVfF+IGQY4PrEDcYEOoCuqsx1AVRcCewIWiuvqeWiXEqP0eX7Zdj9OwhZ3Bgps5wjQkSu1sfsQ9nJVPDoVrJebtzsAgl5hBjOb2W+Mv4YYj2dzAgFGqkq7Dd7VMhS66IX2pHmWYinC9+hsOaSC9YQN669RybSLEnuix82wkQ1OGe57ut9AKn9pTHhztPEdhO9skdA2+2xVhgrQs2h1XS/hpbhyhaBwEiUzK3rhnHTXQVPAqavzfgOe/Wnr1gQ8JhM4zrysMFsEcagdIph3gAYQYEEOm15QmgctOpFuxbIfl5JPIx42fik1u3y6utDMpU5hfn/jrqo82V4fMwgwDRCu1ItSiTs5E84bhGZCZB+ZozAtN/HXjggdsGX8REtFkFjnRz3xiGfcZ5Wd7VphEARnj39oBYhnYdTg/Dnmd9xTrSsC5D+8v4AZC5izD5s/x6ECBxEJnPZUcrzRPNr3V9WlB+7qgXADPPRQVKP4/n6A7W9sTvkgB5uPI60iyfaxRlb3rEIx6R2BthYp4TVy/Dfp0l38cNAiSMGcrT1OiyPv3pT2/j387Gsns17yG1BewimPj5OyBgL/ar58/LfGa9K8OW96wTrUrmHAHrvf/975/GrLJMIf6WNCrTLe97AwJ9YmUb+vRaDpnJpRbd3gCcD8hlIWru5xETwRis2bVLOAjfddcPMYnTtb2qrANre3TIz3iPchJajLEOPitdhCmfu68GJBIJ/kg9kPNYiVmowjdrThyN9NoKNeSZAdeuXxJa7c9xGcTeXCLrkzere2DkYrr46qbHEn+Ns33UStWAREFDu7vPPvskNXNeGeKlAb/kvxF3mT4iyDf/KU9+7xpbjWdYnGNra8ayrrLr/Xnj0hjNjYjMDjsg/uaSqLB5+DLdXoBIaI899kgSDRne+VHYRD7ZKjNY9f2sypZl0XIXBSRPE8dwwpytGMTp2PrWx/B8LiB5Bc1CzR8swsjQpxp8GVOLy504ebz83TKuzSeoRhCgdjxQDpLemIBI0+yfEINzYO82hzp+vGTvXXSYC0geEY/WBYm7ur5zSIicXAAQfh5v2dfW1LVKJz6UA++svMcApKwvboGNcXwCELWOMnJl+PQw++sFSGzjOvjgg1MSZWuMzMLP8lnqpcpSneRWJ8qQlyO/j+djs6y2SjoMk4rJ2ZE1rhoQbMkxrLpgaFJrMlhFmLA6iXN7g+Dz8h6jh8ijKz+9dbfddkvir0nrrLBR1rmARGb4odWwoSf7RIbL8MNQbt6WtqhLlGEsQCK9Np863lzFMSM1ysq5gEQmDoAx0fER4S5WFWFX7QOEMtAXCfqMIctgWSXoOMuuu+6aOIsNRfNcFSAy8fUBgNRM+uZlOvZ7lSb12dDfx62ihyiPySPa5TP6rnJWAUId7lQ3J0qbTE3NaTDEylrRMsoPEJO3fGJYtvAIu4jvcxa0v9bb5x1xWwWI3UEkha492YsUdtG4CJgTMb+elzYgTHRr4wwNRxS2NGCJYN5hCnMB0eosJOlyVu1qCzWPGMt4b2yj1PM5DI2I7+dZW7mt6CGUdZkIyz451+hGOZk8RZjw5dGmxaZXQ/gIR6vh4H409DGBWW4uICrisC5yfpyZ21a5WZms6p0B3SZMZfWzRYHfJQ5bJCPGCxc/4duI7KsHESb326xLaDRs7cvLYUItXnwZu4smcwERESDQdQbvVJ1G4mf9wVldPm3h59qztkZk9S/Chm/gNbaUztc8hYlwcd02J9NDWMpE/g5TcPwgGtppxrWVx/MqQML+irp6yk4l8WtSl19odvnhckJgxxE2/DxsxOGL512kGeG7BIkIF3GsvQAE+5rlqgDRLSW29957z0pr494FOIwc2CYjMrZnPUULpygcwwGFiZLjbplPzXJVgFiAMdv0mdHcIiQqFBmU9/F86j7WYkueMZKBG2Ugfu/48jEcG7EQe4E+y1UBQnqh4dVL8MMjm7NZlH2Ww2R84cfKp0WleXOGGjpopEBGu3kDuvSqABGQ8YKWE18oqOkNNWFqKrXMMAZghyOTghi4mfhiWxph3/K3hWfqilWxQqmZVFcDooC6sAkiDaaKbKIricYqhpGd9e9ZX48bUles3mKeCaFzYGpcNSASIw4anMjuzlNsM1TOK5xf1xRmmWGiLKUfn8Wz8hnvhpQjj+uabQHDOg2YvXGt0rMakMiQAs9po7ohcbhtVjukQuuKo9fj777eMJajfabd0HBxk9wkNc8jaJo/qwYkImFdpAbmLUChBc6PEo9wU/TbCEA1zrIylqKVW7i2sDV1QhuaAWAwAqFyyd28dHsDInGTIepueiAZ83OL9bwAU762HmIdxYdgNLRFnAmpXcC2SGBTlJbAmAdAmecgQCQCFHarREYSCgnMmvuyviVYFrz2fhZBSI6It+iEFxtHB3MXDdRnV423s/LuKv9gQCQoQ2OIvSImViY/dlUxz5w3Aeoq0LKf50SijTV+8Ic4M3wGg8xnSVKOxyUktAk7tekvBEhkortSCbCw0FtoOU2w7D3EFmpcTqia8EPDyCfyigOf2Qv0ccZMSkKsmp2BSaVvpdgWUStNdeVXBUhUoCsRz/FgxmHWHoCh6wLGZ1LphWr2IdbkI6/acHl52+LQXzEM72rReRzXWJM96A75xJ6A4cAdK4LSKMPn+ddeVwFSk1gURgthIGYPIFUENhbWKizBAWZPYOkifvjl+7if9z7C1fjGwS5tbcTXkNihmcVb41AXJ6+ah1E+miAr01jlGgWQtsIAxhKpVTnzFZsgiclmxeYx7JTs+SMYxHhTplPeB5G6nsf7Nr82DlMdaxzGQWsYpLAYrC1+2aZGCYkbBJiRdvht+dc+GwWQtsyicIBReMZsWpp1ebtkAxz8l/kOfn7QQQelTTFapTjLdsY3X3VmSWOHFwUqQ4RY7cN22VPZoGTnlEFc4wkgllG+pQFSFhZABn9dHDgWu2yqoYoBCoCMOdT8DLrtP9lzzz3TXkQDqJm0uY/WqVeZDRtc5/0sx1rpNGGzFY8h9F3vetfU+llisgkOdbsyaCxOyGa8zZbZcqzGUTNYRyNUd9f5fUmPrvuVAZIXIMAxEGqltoYZcxCBNbpWibURJY1BWAaiAUvrteGU1hk7IXKWP8/9iOL4vXh+0jQGILy0NQTG0HqtPR0AADBWu+yekNMjv14LIHkBXOcA6UEGfZILkFiEWL+2LQ1bMwHD4vBz36WlTbVw5nuHfq49o1LXA6gv9DRsh4Rkzdy8w5qHsQIbkqdVPT14SKsu67PI/SQAySsQBCFGI5AfYmEbfohnMmrlEjvxo4eymERVAUw/hLZvRGsXR1ytPta4saBF1SV5uce6nhQgAUZX5Wa9j3elL6141pXulJ4vHZAuYiz6vC1+27MuYpdh4770u+Iv6/n/AL8AL5GUGAdzAAAAAElFTkSuQmCC[/img][/td][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUIAAACjCAYAAAD/whcPAAAgAElEQVR4Ae2dC/xWQxrHdZHuISmiVJ+UpdJllYokJCHEdpXL5lphVYS0FNEFbblESKTcSrJZ69K2SaTard3UiqxE92wibdLOfr5j57/nvPfznnfe9z3nPM/n8/ZvZs7MmfObmd/cnnnmACUiCAgCgkDEETgg4t8vny8ICAKCgBIilEogCAgCkUdAiDDyVUAAEAQEASFCqQOCgCAQeQSECCNfBQQAQUAQECKUOiAICAKRR0CIMAdV4F//+peaOXOm+tOf/iQ/wcBqHchBdZUkEiAgRJgAlEy83n33XXXHHXeotm3bqgMOOEAde+yx+i//l59gYKMOHHXUUerll1/OpHrKMx4RECLMELDly5ercePGqS5duqjy5ctrsmvYsKG65ppr1AsvvKC2bt2qXn31VcXoUEQQyAaBZcuWqTFjxqgzzzyzpDOlrl1++eXqzTffVL/97W9VqVKlskla4qRBQIgwCUCfffaZmjJliurVq5eqVauWrpg1atRQPXr0UI8//rhau3atKyYEWK1aNU2GrgBxCAJJEPj88891HaNOUXfMKPK8885Tzz//vNq/f78rJnUMkuzZs6fLXxz+ERAi/B+G27dv19OO6667TjVq1EhXygMPPFB17txZ99IfffRRWrT/+c9/pn1GHoguAt9++62aNWuWoo7Vq1evhPhYXpk4caKeVaRD54033lCVK1dWs2fPTveohHtAILJE+NNPP6m33npL3Xbbbap169YllZL/4/f222/H9ciZ4krPLVPkTNEK93NsoLGW3KpVq5I6xnoy09w1a9Zk9fHDhw9XZcuWzSquREqMQKSIkFHd/fffr0d5jPaYijRu3Fj30CxC79ixIzFKHn2bNWumbrzxRo+x5PEwILBy5Ur1wAMPqLPOOquE+A499FA1cOBAtWjRopx8IrOX008/XfXp0ycn6UkiKtxnjVnHmzx5sl7XY30P4mO9r3fv3nptZt26dVbqgGyaWIG1KBPdsGGDeuaZZ/RaMhsZZp2PteXXXnvNWp5ff/11VaFCBTV37lxr74hSwqEaEbJzyw7u1VdfrdjRpVKy63bOOefoHV92fkUEAT8I7N69W5PPgAEDVPXq1UuIj02Mp59+Wu3Zs8dP8p7isoRD/Rbxj0CgiXDv3r1areCWW25xrcGw+Mw6Crp+hZSpU6eqhx56qJBZkHfnAAGmtCNGjHDpijZv3lx3rl999VUO3pBdElu2bFEdOnRQ/fr1yy4BiVWCQOCI8MMPP1SjR49WZ5xxhipdurTukX/xi1/oNRh20oppkwISZFFcJFgIrF69Wk2YMEG1adOmZMSHMvOwYcMUa4DFJHPmzFHlypVT8+bNK6ZsBS4vRU+E7Kw9+uij6uKLL1YsOjPdrV27turbt6+eiojKSuDqXNFlePPmzeq5555TXbt2LSE+ppy//vWv1fz584suv7EZYkZUqVKlWG9xe0Cg6Ihw06ZNWpm0f//+qn79+rpiUsjnnnuuevDBB9WKFSs8fF5xPMoolQ0UkeJA4Mcff9QjqEsvvVQZ7QE62G7dugXyCNvGjRtV+/bt1ZVXXlkcAAcwFwUnQhaXGdYPGTJEtWjRoqRHPuWUU/S6zIIFCwIIqzvLTJHr1q3r9hRXXhFgSeWmm24qOSUE8bVr107PNnbu3JnXvNh4GYraZcqU0WvmNtIPe5oFIcL3339fjRo1SutCUSH5NWnSROveseaxa9eu0OFeTGuXoQM3wQehOjVy5EjF+rGpYygy42dLbSpBNvLqNXjwYFW1atW8vjMsL8sLEX788cdq0qRJ6sILL1QHH3ywrphHH320uuyyy7QO1pdffhkWPNN+hxBiWoiyegBl+IcfflhPEQ3xsaZ8ww03qCVLlmSVZtAisYN98sknq6uuuipoWS94fq0Q4ddff61uv/12bamlZs2amvgqVqyopyKDBg3SmxxRtN2HEQcaqdguzI3dxvHjx+t1PUN8/EWROco7qC+99JKuY++8807BySVIGbBChCg0Oyun/F/s89mqAyeddJKaNm2a4uy4yM8IsBbKaFgkcwSsECFqB1T8sWPHZp4TeVIQ8IhAnTp19OkOj9FC/zhLTXQQ1157bei/NVcfaI0ITzzxRE2Gn3zySa7yGpp0WCc87bTT1F//+tfQfFMhPgSTVCjVi32+ePRZfmEwwhKUSHoErBHh2Wefrbp3765QgxGJRwDrNEKE8bh49YEEafCCZTxyrMdjbEQkPQJWiPCbb75R27ZtU/v27dOVlEVtEUHABgJYceb422GHHWYj+UCn+cUXX6iWLVvq46eB/pA8ZN4KETrzPWPGDE2Gn376qdNb/v8/BJi6yGjGX3VA9xQTWGKfLx7H6dOn6/a3cOHC+EDxKUHAOhHypgsuuEBbySh5q/ynBAGsh4hhhhI4sv4PZ9GZIq9atSrrNMIa8frrr9cnasL6fbn4rrwQ4b///W9dSTkrLCII2EAA9ZkjjzxSHX744TaSD3SaXBLF5qVYTU9ejFaIkKM+WIF2CtY96LHDerzJ+a3Z/l8s6WSL3M/xuG6BKTInlkTcCKBrSftbvHixO0BcGgErRIgeIbvGscI1hR07doz1FrdSuvHSa4v4Q4BjnDR4UduKx5E7uNlYEolHIK9E+P333+tKitFLETcCbJjIpokbk2xcmNjiXhp+Im4EuKu7adOm6uabb3YHiMvO5U3JRoTgzUU39NgyDZTaZwsBo6kg9vniEeZeFdpfVAxRxCOQ2MfKiJCLrNElTCZcptSpU6dkwZH2R52GUyci/hBgGUY63MQYYvRY7GO6sbFChO5XxLsgSirpxIkT4wMj7sP0mN09MdflryKgqcAOMjvJIm4E0Ok9/vjjFSb+RX5GoCBEyKufeuopTYbr16+XshAErCBgdkqxhiTiRsCYhFu2bJk7IKKughEheHfu3FlxH6xIPAKMCGVTKR4Xrz4swzD74F4PETcCV1xxhb4XyO0bTZcVIvzNb36jevTokRZR1hGppFgWFnEjwBS5WrVqspPshsWziztxOIcsaiPx0KFi1LhxY8VF8VEXK0SYatc4FnAzRI+Suf5YDJK5ZZ0wGTLe/J988knd4XLUTMSNwOTJkzU2Qbwd0v0l/lwFJ0Kyz/SYabJIYgRE1SgxLl58qV/MPrjbRMSNQL9+/RQXW0VZioIIt27dqispF7mLuBFgVMiFV1OnTnUHiMsTArt379bm67k0TMSNwJo1a1TDhg3VnXfe6Q6IkMsKEX733XfK612xZojOTVwibgTEyrAbj2xdpo5hsFTEjcAjjzyiByN///vf3QERcVkhwmyxO/300/XNd9nGl3iCQDoEUORniowuq4gbAew5HnfccW7PiLiKigg3bdqkKyk9t0g8Ath1fOihh+IDxCdjBDjvfsghh6hjjjkm4zhReZD7x+vXr6/uuuuuqHxyyXcWFRGSKzNE525kETcCkOCrr77q9hSXZwQmTZqkO1zUvETcCHDaixHz6tWr3QEhd1khQo6IXXLJJVlDh9Xmrl27Zh1fIgoC6RDgPDcNnk0UETcCXIjVpEkTt2fIXVaI0IseYSJ82TChkj7xxBOJgiPvh7K1jAz9VYNdu3ZphXWmgiJuBNgwwSjDqFGj3AEhdhUlEYK3GaKzbijiRoA7Trp16+b2FJdnBFhqoMMdOnSo57hhj2CwiYqB26IlQipa+/btFeaURAQBWwhw7zbm/bFWI+JGgOWtqFhNt0KE7Mwx9fAr3MtKj80RKZHECIhV68S4ZOqLGk3VqlVVgwYNMo0SmedWrlypz2iPHj069N9shQhziZoZom/evDmXyYYiLU6bcOpEziT7K84xY8boDleMD8TjOH78eI1N2C9dK3oipGjatm0ra2LxdVT7yKmTJMB49KaOMUXmWlARNwIXXXSRatmypdszZK5AECG9EVNk7lsQEQRsIMCounLlypE3PpAIW5ZfjjjiCDV27NhEwaHws0KEnOXs3r17TgF64IEHVOnSpdWWLVtymm4YEsM6DYvaYqXGX2nee++9usONsvGBZAia5QPW7cMoVojQrx5hMqBbt26tuLdWxI0Aoxm558SNSbYu6hgdrkg8AhzxBJ8wSqCIcO3atbrH5kpQEUHABgJYTa9UqZK23Gwj/SCnuXz5cn0hFrOzsEmgiBDwWacoW7as2rZtW9jKIiffw4F52UX2B+Xdd9+tO1z+irgRQJWG9foNGza4AwLuskKEP/zwg9UznK1atcr5GmTAy1FnHwLkaJQcv/NfmtQxmSInxpFDDuyyh0msEKFtgLCMQa/07LPP2n6VpB9RBLZv364qVqyo7/+NKARJP3vp0qWqevXq6ne/+13SZ4IWEEgiBOT77rtPlStXTlFhReIRYHQoU+R4XLz4DB8+XHe4UThZ4QUXnsUgA4ORsNgCCCwRUhjNmzf3Ze7La+EH6flmzZrpneQg5bkY80odK1OmTDFmreB54s5ozmqHQawQ4cCBA/Oi5oK5IHql6dOnh6EscvoN6BTKiNA/pGzKlS9fPnL2+TJBbsmSJfqIZxjuJbdChLb0CBMVzj333KMrKmoPIoKADQSGDRumO9xx48bZSD7QaaKlwGCEmyiDLIEnQsBv2rSp6tGjR5DLwVresV2IIqyIPwRYapApcmIMuTO6Y8eOiQMD4hsKIlyxYoXulWbMmBEQ2POXTYwyYMFHxB8CHO086KCDFIQo4kbggw8+UFWqVFGPPfaYOyBALitEiJHLPXv25BWGkSNHanUHWRfLK+yRetmQIUN0hzthwoRIfXcmHztixAiNzY4dOzJ5vOiesUKEhfrKE044QfXq1atQry/q97J5EsVrGnNdKNQxTjaJxCNwxhlnKH5BlFAR4bJly3SvNHPmzCCWhdU8M0VmWicjZn8wozeH/mqLFi38JRTC2IsXL9azsiBeuhYqIqRusTmAXTlMsIsIAjYQ4D5kdkofffRRG8kHOk2jhL5z585AfYcVIrz++usLalH6uOOOU3369AlUQeQzs2LV2j/a1LEDDzzQf0IhTIEdZHaSgyRWiDCfeoSJwEbRkx77xRdfTBQcaT+sDYONkKG/arBx40ZNhBhnEHEjsGjRIr3DHiSL8qEkQoqFITq3k+XiNj13MQffJTff5aYMb7jhBt2pTJkyJTcJhiiV22+/XWPDjZZBkNASIeAfe+yx6tJLLw1COUgeA4pAo0aN9OZJQLNvNdunnnqq6tq1q9V35CpxK0T4448/qr179+Yqj1mnwy4W08CXXnop6zTCGpHdY+45EduF/kr4q6++0lPksJqw94POwoULtarRtGnT/CSTl7hWiDAvOc/wJdxVy92/QRmiZ/hZOXmMEydy4ZN/KAcMGKA73CA0eP9f6y0Fc0473wcsvOVSqdATIYA0aNBAXXbZZV6xkecFgYwRaNiwod4gyDhChB5s166dOv/884v6iyNBhO+9957usV955ZWiLoxCZY4jYzJF9oc+d3hw4iRsJuz9ofJz7AULFqhSpUoVtbk8K0R47bXXKu41KCa59dZbtXnx3bt3F1O2iiIv3bp104roRZGZAGeCes+atJxsii9E2h/YsH9QjGKFCAutR5gM6Hr16qkrrrgiWbD4CwK+Eahfv75MkZOg2KZNm7wYbE7y+pTekSJClIjplWbNmpUSlKgGspMsOob+Sn/9+vXabmH79u39JRTC2PPnz9ft74UXXii6r4sUEYI+ppRq1KiRdzNhRVfyCTJ04403ir29BLh49erfv79u8LImHY/c0KFDNTb/+c9/4gML6GOFCH/66Se1b9++An5W6lfXqVNHMX0XcSPAiFCs07gxydZ1zDHHqAoVKmQbPdTxfvnLXxbdpWtWiLDYS/Gdd97RvZLslBZ7SQU3f+vWrdMXxHfo0CG4H2Ep56b9vfzyy5be4D3ZSBIhMGFKqWbNmgpr2iJuBOggGNHI6NCNi1fXlVdeqTvcuXPneo0a+ucHDx6sVWqK5UMjS4QUQO3atdVVV11VLGVRNPmAALHrKOIfAZZhKlas6D+hEKaAcduePXsWxZdZIcKrr746EIet//jHP+oee86cOUVRGJKJ8CHwj3/8Q0+RO3XqFL6P8/lFb731lm5/s2fP9pmS/+hWiLBY9QgTwYUppSOOOKIojEQkyl8h/RgZ3nTTTTJF9lkIHO9EbevNN9/0mVL4orNEVQwGbiNPhFStWrVqKU4FiLgRgAi550QMM7hxycbFMkylSpWyiRr6ONSxQluUFyJUSs2bN0/32K+99lroK518YGEQWLVqld4cCJoJ+3ygxUiZEXMh258VIty/f7/iFyTBlBK9djHrPxYST06cyC6yvxLo27evbvCcsBBxI4Ayf/ny5d2eeXRZIcI85j9nr0IJ/PDDD1fXXXddztIMU0LVqlVT2C8U8YfAkUceqW9Z9JdKOGNzZ3ShzOUJETrqFPpeDNFff/11h6/8FwRknTA39WDFihV6ihwUE/a5+erMUnnjjTd0+2OpKt8iRBiDOJsmRx99tGKEKJIYAZkiJ8YlU9/evXvrBv/+++9nGiUyzw0aNKggI2YrRMih8y5dugSy8LhrpXr16oo1Q5F4BLBdyHqOiD8E0FSoUqWKv0RCGBtjDNwZzamcfIoVIgySHmEisDlixhT597//faLgSPthykxMdfmvAsuWLdNT5GI3Ye//S72nQLvLt96lEGGScmJUW7duXVVs5oKSZFe8A4hAjx49dINfunRpAHNvN8vMyNigy5cIESZB+ocfftC33w0cODDJE9H2ZmQo55H91wE0FfLZ4P3nOD8psEbPveT5sgVghQjzA5X9t2AmiCE6u1kibgRYPmC9UMQfAh9++KGuYxdddJG/hEIYG+0N2t/bb79t/euECNNAzB0n3HUiIgjYQuDiiy/WDf5vf/ubrVcENl30eg899FDr+RciTAPxrl279O4exhlEEiMgBm4T4+LF97DDDtNLMV7iROFZbr3jXnLbBx2sECEbDGHaZOCyGYbof/jDH6JQ9zx949SpU/Ualyhce4It7uFFixbpOvarX/0qLizqHpxBpv2xLm1LrBBh0NVnEoHdr18/3TMlCou6n5BgbmoA64Q0eGwYirgRuOaaa/QRWLdv7lxChBliyWkKLA2LMnGGgMljWSHAetghhxySVdwwR+JKDa6PsKXFIUToofY8//zzusfGsrWIGwFGhQcffLAoW7th8exasGCBrmOFts/nOeN5iGAOOixcuDDnb7NChOj+nHPOOTnPbDEkyDnRhg0bFkNWii4PWKeRc8j+iwW1JKbIn3/+uf/EQpYC3IJF+VyLFSLMdSaLKb3t27dru2mYGBcRBGwhwOiaM+8ibgQ46IBRlFwvUQkRunHOyDVt2jTdY3P5jIgbAUaE3HMi55HduHh1mbt/C2Wfz2t+8/n8rFmzdPvLpfUeIcIsS5Bzoo0aNcoydrijMbWzqeoQbvT+/3XnnXeebvBff/31/z3lfxoBNFOOOuqonKFhhQg5Jxh2e36bN2/Wt2/dfPPNOSsMSUgQiEWAc8g1atSI9Y68+/vvv1dY+85V+7NChGHUI0xU855++mndYzONEYlHgJ1kmSLH4+LFx1xshDUkETcCxhYA57X9ihChTwQ5J4ohSZF4BJgiyxpXPC5efdDAYBeZjToRNwIYcEW/0K8IEfpEkPWb0qVLqyFDhvhMKXzRRZUmd2VatWpVVbNmzdwlGJKUsAWAte9bbrnF1xdZIUKOw5x77rm+MhakyFOmTNE99rvvvhukbOc1r0KK/uA2Vpu5U0fEjcCLL76o2x9Wv7MVK0SYbWaCHO/CCy9Uxx9/fJA/wVreMeB64oknWks/KgmfffbZusF/9913UfnkjL/z8ssv92ULQIgwY6hTP/jll1/qSjp06NDUD0YwlE0TUafJTcFXrlzZysmK3OSucKns3LlTG2W47bbbssqEEGFWsCWO9Nhjj2kylEafGB/x9Y/AnDlzdB2zZXzAfw4Ll8LMmTM1NtloKlghQowp8ouioATbpEmTKH562m+mgjKFEfGHwJlnnqkbfFTbWCr0MJfHXSdexQoRRkWPMBHYHJRH1eHWW29NFBxpP6bIqNTIxon/alCpUqWcnqzwn6PiSIG6hbXv4cOHe8qQEKEnuDJ7+OGHH9ZkiEklEUHABgKvvPKKrmNi/CMeXWMuz8sdMEKE8TjmxAcl2BNOOCEnaYUxkWeeeSaMn5XXb+rUqZMmw7y+NCAv69u3r6eDDlaIkItWzj///KKDDDUOzBsxdeXn3NQgzPibvx06dCj5BobcmP7hOe7pSCeffvqpTq9r167pHo1cuFnUpqMwul87duxQ7dq1UytXrtR4cJYb9+rVq7V7w4YN2v3ZZ59p97p167R7/fr12o15e57ftGmTdjMawG1OYyxfvly7v/32Wx3OsSzC9+zZo90Y+8RtzsijE3rKKafoMP7hqBvEY2Tu3LkKdRYjWERhfdgI39i9e3fjVM8++6zq2bNnifupp55SrGcZYaONJSUjEydOVE6dwfHjxyvnBWL33XefGjx4sLaaXqdOHTVy5Ejl3DFlajhixAiTnF6qGTVqVImbkeSYMWNK3Gy+PPjggyVudIEnTZpU4uY2x8cff7zEDdFwxNQIRkimT59unAp1MvT7jKBXPHv2bONUZ511lkI30kjHjh2V0+Bx+/btS9rnvn37dNlwrwuye/du7V6yZIl2s2NM2ZlNEuoG64Sc077rrrvMK1L+tUKEKd9YoECOejVr1qwE3NhsEM4PcjQ/AyzPOu2fEe4Mi00LN2SJ2XVI9c9//nOiRyLjx9qgc5ME7CARMP3kk080DpwQwE0lRr755hvtNkS3detW7TaWWDZu3KjdW7Zs0c+jvkR8CBVhrRa3Ib61a9dqN40IgWAJ37t3r3ZDnLj379+v3X/5y1+0OTHtUEp99NFHrtNDixcvVsOGDTPBCiJ1rktRR5yNkLt577nnnpLnuQjs/vvvL3Fzhy9kZwRrzBMmTDBOxblallyMQLSTJ09W5mIxOtwnn3zSBOv65xx1o/TvJCqIl7hGID2m20YwsssOtZFx48a5iAsipnMwAsk6z9wzYHAuDd1xxx3KEBlxWEN3nhGG1E2nSDhlsWLFCp08nRPuVatWaTdm+3GvWbNGuzHAwNoz5Fy3bl3d5jiJA/lmeid5JIiQSknvQINMJoz+KLxk4gxjdEhFSSUUCO/t3Llz5JSJwRmbhAZv/oKvcafCTcK8I8Boig43SvLBBx8oyBVFfb6dQQedK6NgRpp0nF4kEuiZ0V4qYGioEFcygQjNKJD/p2rUjAbNtJopGwXlnLYke0eQ/Rn9OPHj+w1eQf6uoOSdi8Xq1asXlOx6ziejP0bMhvTLlCmjTj75ZD0yZHOEpSg/YoUImW6YtRc/mctVXBolQ2lGKfQgp512mmvawnsYweFvfkxLYtU8IDgnISbLH2k5Lz1n7QUyfO+995JFCZw/WDi/kakJfiKFQcDslDJKCoOwRsw6KleclitXTrcfrDyxxPLII4+opUuX5vQzrRBhsekRQkz8aKiQGyMX1gshRyM0asIJ4y/kiXmfWDI0zyf7S3zeFSsstDdv3jzWOzBug4/JMKNs53KB8Ze/hUPg1FNP1YRRuBxk/2YGT2ymYFYLKzsMHDC8esEFF6jRo0e71h+zf0vymNaIkCEsC9rpfsmzlrsQiCm20dKwATuZQIDES7cWGBsfgnASrAn/+OOP9fuC0mMzrXWO8MCPbxMpbgQqVKjgy/hAPr9u/vz5eue7cePGum2gJA5vsJHCLjybIvmS5EzgIweMCBnGMr1M9RswYEDJLp+P16WNyujO2aiJQENPRYQ8Q7xYAk33MjZlkq2NjR07Vr/TuXuWLr18hUP8zl1O8GLULBIsBMzFYs6yLJYvoF2wc87aHm2PX4sWLbSaEKo4RgOgEPm1QoQQHEPadIIek1F3SPesn/BEoxlGhJBWKjHT6VTPOMMo6HRpsgbZsmVLZ7SC/B/ic66Dkne+N9UmUEEyKi/1jAA6eKVKlfIcL9cRvvjiC63y06VLlxLia9CggerVq5eeafnd4Mhlfq0QYaYZzBcR0ughKNPwIUE2TcxoDxKgBzV6T6zzQeSMiIibqTCNZtMglaAwTE/o1DlL9Xwuw9ArM0RnMOHbRcKHQPny5bMyPuAHCRSb2bTp3bu3bm/Uc+5mhghpX049QT/vsRE3EkQIcDR4SApChOAMCRIGObD+xYiIwiMctxcSJB3iONNNVmAoo/IelHJtCgqxkLoRryNcE0/+Bg8Bc7HYvffeazXzKCwzAzRtp2zZsqpt27aKkyusAQZFIkOE+SgQ1hSdxJPqnRzfatWqVapHPIdB9s73Z7PG6fmlEqFoEYCQcj1FjlVkpkPHMjv7AnS85mRO0YKSJGNWiBAdQnOUKcl7tXe+psap8pDLMCqFmXqmS5cjXDzvPA+aLk5sOO9imm+E3ep0U3PzrPyNBgIHHXSQYlc2W4lVZKbOcrE6tzeyMcNRyDCIFSLMVI8wjETopVKwg0bFopfNRCA+5/lP1iSZkogIAskQeOKJJ3Qd46xwJpJIkblKlSraSALnkdkACaMIEeaoVJmWQmpeBVWCk046KWE01iidxMe0l3d4XbtMmLh4RgaBNm3aJJ0iJ1Jkpo61bt1aq7oYa0CARb0zG4rJwKOz5pnYX7Lni8Xfe8vNIOdRHBFCUtno3XFUiIpnNlmoQGZ6zV/CnOt+GcAvjwgCcQhwTM3cshiryEwdQ++Xu4FTHQNlzZlnUwn1mGdif6niFENY6q/KMoeDBg3SZwTZRcXumPlt27bNlWLTpk21JrkJj11XxLSQCeOvU7ivwRkWq7fIVr4znC19p2DOyRnev39/Z7A+xO0Mjz0tQk/pDO/Tp0+JoQUSYrrrDHfagiMce3cmHN0qKg62Elnc5gA9/+fHLrf5v/z9GRPBITscnBYco3oAAASgSURBVORUu3Zthc3BefPmuep9MgcEx/ozaaQSnjOdeqrnii0s9Vf5zC0WVyAY84tdWMUIggnjb6yhBgxTOsOd2cFYozMs9lYv7Ns5w2Ov2USL3Rl+5513OpNX2MFzhnPe0SlYlXGGxx7Fw5aaMxz7b06BKJ3hLGijbI2BSWP4Qf7+3wiGYJEbLGbMmKG83ovMsg8dcrpjqdRvyNILETLr4RQT0270fNE3NHYUnX5GB9jZhnL5f6tEmMuMSlqCgCCQfwQgIw4fQIJmjTpVLpg+xw4KUj1PmozwicesCxJlA5AZHu81fiw70RnaEiFCW8hKuoJACBCAiFjiQjIlQgiMKTTWmyC0VGvcJk2nLQAz8nSOLM16uVk/zzW0QoS5RlTSEwRCggAkxeiMUSFiSCvV50FUPEcc/kJmTKuZXieSRGkSFyIlzCmJ/Jzhfv4vROgHPYkrCIQUAciIKauTjBKRViafH3uk1RknWZqJNmWECJ3IJfk/gKJ6YnqvJI+JtyAgCGSAACM5iCfZzzltTZccU2szvY59VogwFpEs3JAeprspLHodo+fEbrRIcSJgyihRA0vWuExjiY2Dv4gdBMwUF4zNj00QygC3WavjutR054uZXifbQCEt0oyVZH48b0Pic2DjLRbTBGBTKLzGnPBItiZhMSuSdJYIUH5UfGc5OpOi8mejrO5MQ/7vH4FEpFWrVi1tbcakjvoM6i/MzvjLTm+qskuUJmkJERpEffxN1QORrBl5sFOF3pJTRymRn4+sSNQMEEg1dSI6u4iMJL1IqjKm8VHu/JKRr5d3ReVZBhex5cBdPNwzYoSBCc+YX7KRoHk+UZqExb7H+Nka4AR+RGgANX8Bit4kFWCE01PRAGkwEKdR2DV+9GJs/4vYRSDRonzsGymjRA0j9jmn25SxUfAlPuXJUgr/J03C2BCQdWUnctH8fyiI0PTwrA1CYE6dpETFSiMxIwbCzdTMuaBL4+A50haxh0AmJMczEBZExl86LUaJqYSyS1SesYSabvaQ6h0SFh4EQkOEVHoqOUQIIabq5RMRXCI/0hIitFfZzWgwXcfFc5QDo3z+8jy6aaniJStPZwfIl5nRob2vlJSDgEAoiNAJNI2GXj62wjufoZHESqKGQyMRIoxFKnduiIyyykY48RA7unOmk6w8Y+uFEKETtej+P54RQoAFlT1dI4n9zGQNR4gwFqncuf1MS5kapyLRZOUpRJi78gtTSqEkQkiQEUMyoZHESrKGI0QYi1Ru3GZ6m2wJI9ZkW+xbWQphsyOZJCtPIcJkiEXbP54RAoQHJMUuoNFbQncJd6qzjXyeEGHhCzlVZ9WzZ09tlxFTagjkhYoT5euljGM7sUTT4ER+hUdHcpBvBAJNhIwmzDSYCm0aVzrdMJ6LFfxiVW4YVcb6xcYTt3cEKB/wTlZOw4YN0yaYTMpMgxn9EYcf5ZIsromTrDxjN1hIK9bPpCF/o4NAoIkwOsUkXyoICAI2ERAitImupC0ICAKBQECIMBDFJJkUBAQBmwgIEdpEV9IWBASBQCAgRBiIYpJMCgKCgE0EhAhtoitpCwKCQCAQ+C/gu/A0SWaRjgAAAABJRU5ErkJggg==[/img][/td][/tr][/table][br][br]Which measurement that you need to calculate the volume isn’t given?[br]
How can you find the value of the missing measurement?[br]
What volume formula applies?[br]
Calculate the volume of the solid, rounding to the nearest tenth if necessary.[br]
Calculate the volume of each solid, rounding to the nearest tenth if necessary.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAPwAAACOCAYAAAAVQWWtAAAaFklEQVR4Ae2dCfROxf/H65dQJKlUiiwhadOiQ9JGaBcqxUkSSiuVSpRUIipaCVFURDsq2lQISSotSiuJqIRU+PzPa85/vl3XfZ7vfTzL3T5zznPuc+fOnZn7nnnPfGbm85nZTtQpAopAYhDYLjFfqh+qCCgCooTXSqAIJAgBJXyCCls/VRFQwmsdUAQShIASPkGFrZ+qCCjhtQ4oAglCQAmfoMLWT1UElPBaBxSBBCGghE9QYeunKgJKeK0DikCCEFDCJ6iw9VMVASW81gFFIEEIKOETVNj6qYqAEl7rgCKQIAQST/jPPvtMPvjgA1m0aJH88MMP8ttvv8nGjRsTVAX0U5OEQKIJ/8QTT8h2223n+dt5552lYsWKUqNGDalVq5bUq1dPWrRoIeeee65ccsklcs0118gtt9wiAwYMkIcffliefPJJef7552X69OlbNCCrV6+Wf/75J0l1Sr81xAgklvCPPPKIIfruu+8uvXr1kueee07GjBkjDz30kNx9992GzFdffbWcccYZcsghh8hJJ50kxx13nBx++OGmEdhrr72ERiFVg+H2dzYgxEFcfhuQ2bNny6effirfffed/Prrr7Jhw4YQVynNWpgRSCTh77nnHkPULl26pC0bRP0777xTli5dmjbc33//LStXrpRvvvlGFixYIO+9955MnTpVJkyYIKNGjZIhQ4aYeG688Ubp1q2bXHTRRXLOOefIKaecIg0aNJCDDz5YqlatKjQ+JUuW9NWIZNqAIM3QqL3++usyc+ZMWbhwoSxZskRWrFgh69evT/t9+jA+CCSO8LfeeqshVI8ePdKW4pw5c+SOO+4oluxpI8niIcMAenNISSMyY8YMmTx5sjz99NMyfPhwuffee6Vv375y3XXXSdeuXeXCCy+Us846y0giRx99tNSpU0f2228/KV++vOywww7FNiJ+GxCknwcffFBGjx4tEydOlFdffdU0cOTx66+/luXLl8vatWuz+HJ9NZ8IJIrwkBxR+7bbbivClN7+ww8/LLrnT9Bk3yIzObz5999/ZdWqVfLtt9+aHh5JZMqUKfLMM8+YRmTQoEHSp08fufbaa6VTp05y/vnny2mnnSbHH3+8HHHEEVKzZk3ZZ599pGzZslk1IB07dpSrrrpKbr75Zrnrrrtk6NChRhJCIiI/NG7z58+Xr776SpYtWyZr1qyRzZs35xCJ5EaVGMLTC0L2wYMHb1HaxxxzjIwfP77Iz5L9p59+KvLTP6kR2LRpk1nZ+P777+WTTz6R999/3wxnwPSxxx4zeCNV0Ygw2dmmTRtp3ry5HHvssXLooYdK9erVZc8995TSpUunbUTcEkijRo1MPK1bt5YOHTrIFVdcIQyZkMruv/9+GTFihGnIXnnlFXn77bdl3rx58sUXXwjl+vvvvwv5TqKLPeHpGS644AJTmQYOHCg///xzyh/jbiqMkj1YKlBmkJJlUiYrmXNg6IAEAJEZziClde/e3Ugi5513npkApRFhgnX//feXChUqyI477piyEbENCA0ODc+RRx65RcMfLAL5Sz3WhEcUPPvss02ht2/fXu677760P8amSvb8VbagY2aegZUYGoomTZoYyaJEiRJmyZWVk8qVKwedxbynH1vC05NTqIw3X3rppZRAMgmFuKcuXgggHbz88stGYkN3onbt2qbhr1atmpx55plmKZa5CxSvcLfffrsJEy8Utv6aWBJ+8eLFZrmrUqVK8tZbb2391Q4flsUQFdVFFwFWBZg7QAGKpVbKdKeddjJiPROOjO+HDRtmhgZ//vmn54cq4T1hCb/nRx99ZMZxtOhz584Nf4Y1hxkj8Pnnn5sJuZtuuklOPfVUs/zIhOxhhx0m7dq1M9qPzPb/+OOPvuNWwvuGKjwB3333XUFkYx2aGVl10Ufgl19+McpCLJ9CZiblIDeKSmhBsrSHbgKTe9k4JXw26AXwLrO4LO+cfPLJGSnLsA6skkAABeaRJHoCzKeMHDnSrNMjjpcrV86I56giX3755YJKNPoDTMjm0inhc4lmnuNC44t1XGbk//jjj4xSYynn2WefzegdDZwbBNAixOCIJbaWLVsa6Yzem2UyNAeZUEW7kAm4fDslfL4RzlH8qHhSSRD3VBsrR6DmIRrW1d955x2jVYcCzlFHHWXKDSMktPlQmhk3bpxR3slD8sVGqYQvFqLgA2DZBtkvu+yy4DOjOdgCAbTuxo4dK9dff70xEsIwiLJCQ47yYkadORcagjA4JXwYSiFNHrBDpwJRobJxaNahTqtu2xHAmpBZ8f79+xv9e/YPoGy4tm3b1ujLo+KK+m1YnRI+rCUjIr179zYVikLK1jVu3NhYfWUbT1Le/+uvvwT7fNa1mURjzRsVVibXWCLr2bOn6dk//vjjSA2xlPAhrcGoRdJ7oE+tLv8IYLHGpCa7+7AMtvfeexv8GYOj5II6MmNztgaLslPCh7D0OnfubCobVljqco8Am3i88cYbpjFlk466desavNExx1SWzUBQU8a8Nm5OCR+iEmVTSWvxhv5zLh0Fzc42SXOYh6KVyCoHpquseWNBhniOLgNzI+ySg8FJEkxJlfAhYQDr6oiS7NrCxE+u3QknnCCTJk3KdbShi4/98Oid+/XrZ7bXotdmaEQvjuT0wAMPGLtxNshIolPCh6DUmf098cQTZbfddjPjxBBkKRJZQAuNJS+WLS+99FJj/gm5WRpDwQXSv/jii2b7rEh8UAEyqYQvAMjpkvjyyy+NTnyVKlW22oIq3XtJfIaJJ/rkKK9gErzrrrua3rthw4ZmzztswNkyCtVVdd4IKOG9cSmIL3vMsQkju7kyS5xPh1ony0xRcdj5YzeAHgI7vbBjC703V7Z6Yn84TILZAFOdfwSU8P6xymlINjBkfMn6LpU734795sM6hmf7a5SCWJVgzbt+/fqy/fbbm8k19oWjkqKLzm6x6rJDQAmfHX7b9DbaWozXmzVrJqk2KtimiCPyEsSl8UGxiEMq9thjD9N7s/0Su7wyo470oyfZ5L5AlfC5xzRtjOw6w5IQu5AmwXEEFaI3O6xi+HPggQcacrMNNKI6/qyJc1CEuvwjoITPP8ZFKTz++OOmsrNfeaEd+7DPmjUr78miasq6NsdXYZLLCTOI56x/06NzKgxbc6kLBgElfIFwZ5KJSScOZwzCMasN2XLp2FoJnQEqERsmsrce38i2WyyTcfwUm27oGXG5RD27uJTw2eHn6212m4EI9HBRdevWrTObI2LuefHFFxdtwcTSGApDbM3EibJs1aQuvAgo4fNcNuxFBtkhRJQce+VxqgpnuqGlV6ZMGfMdzKDjx+476BCoixYCSvg8lhczzpD90UcfzWMq/qLGCoyTTbwcE2bTpk0zWy21atXKnGhCvlEGYqKNQx1ZNsNkVF20EVDC56n8mJiDNE899VSeUsgsWo5sZi0bAx2WvFjzRrecwxPJJ5NrjPOpEBy1XAjdgMy+QEPnAoHiCM+KCnsmslsuy6QoOaWyGmRill8YXcEOokCtkxNAIBEnggTtKCwm6xhaNG3a1Kz/kze0+1BywSpPt7oOupQKl346wlNX2POe1SSIz4+juSG/07EnAMM8wrL6EkZXEMIDBLuhlCpVKhAjGCzu2KSBk2Ox6z7ggANMw8O21ojqrHmjXssEnLpkIpCO8KkQoYOA/NZxiCU9O2cYZkp4TJVTSQz4cwKu08Ept5/zear/eSc8S1RsIwW5MOAohONQArTSunXrJhwH/b///c8QnPVvTivhlFjOHcfRw3NMkbpkI5Ap4SEhhIeo1tldfzge2y/hCUs89sfGIzgbB/es+PArX768aWBoVAhPA4Mfkodfl1fCcyRQvXr1jGFHvvS9IS5DBABCiqhYsaIBo0aNGmaZDDAWLVqUEg900l944YWUz/VBMhDwS3hITX1hHG/J6UbIktXt776nbkJkZ6Nhe3nbEHC1jmEERHemizQB6f26vBEexZKaNWsaYJYvX+43P2nDoajCjDrKOhz/jEUdALA0hu45u6bSW3O4oDpFIBME/BCeXtv2xEzgWXK60/FLeMb6ENbLWcI7nzF8IH0rSfDMShpOP+c77v95ITwZQyec44GyGRdjGsvhBGzBxH7mnC7DBzODjliDoYme5+4uUr3fFgT8EN7GC7kgpLt3ts/9Ep667JwDsO9zJQ4aBKezhHf68T9dPFuFdXtke494vcsuu5jTRDKJC/tt7LzZJx7RZd999zUfgloqE21osmV7YKBXfthWmbPK1CUbgUwIb5Gix4eYbpcrwrvnAUJHeHZdwSCEwwfSOY6EQuTnYECOHeIsMVopJtdY1sCgBXXUXB8Y6JUnxv1s96Qu2QgEQfjiRPpQEx6FFUiL0orbMc7A/PWGG24we9QhARAWk1DCcyRRIQ4MdOdL7xUBi0A6wtOzOifWeIexdypR2m8PbyfcnHHb/15xhKaHtx+PLjm98ptvvmm2YGrTpo1RTgAYNrbAcmzQoEF6tJOtZXoNDQLpCI8mJuN16jHKNlxZEsPfy3mR1SscfoQlPvuzM/BecYSC8ABFZrt27SpHHnlkUcZZ/2Zvc8b0mR7hnAqcfPiTRx3D5wPZaMWZjvD2S5BUIV0+HD2735n2bNLPapaeDDJjzpG/LJMh1kfNUuz00083+7VnA6K+G30E/BA++l8pkjXh6d0xKlGnCEQZASW8j9Kjh1fC+wBKg4QeASW8jyKKA+F79OhhTmnx8bkaJMYIKOF9FG4cCI+STxjMdX3ArUHyiIAS3ge4cSC8j88MRRCWPr2sovDj9Bx++ZpBDgUAec6EEt4HwEp4HyDlIAjrvcyVuDWvuEdbizVbftYeOwdJJi4KJbyPIo8D4THM4XirsDowxvwRhQwn4Vm3pRHguXW2YbD3evWPgBLeB1ZxIDzHJ+fj3Hkf8PkKAsltD14c4W0jkC5iwmDaiT03dgvEjcMfC0SGBfjz3JqA4mff4UrYuDklvI8SjQPhfXxmYEEYt1uSQ0z732YIcd6SEi0wSAppUznCIC0QFyTmZ9VD+c8z4rTPSI84uRIOfyQN915uqdKLkr8S3kdpKeF9gLSNQehFGZNDUpwX4cEfMiLa86OBSOdYkbC62u5wkJk4bHo8t362UcDPlrkznDuuKN4r4X2Umi38KGva0SOywWXYHD2tc1bei/DknXAQEiJDWOc77m+iAUn13JLb+Y6XH89Jh2dxckp4H6UZB8Kza+3kyZN9fG3hgkBuRGl2JbU/9kG3fuAOcSEw/61DKoCMqcbY6YjqRW4vP9JKF4/NS9SuSngfJRYHwvv4zIIHoedGVHf+IDcmmvhBaBoFL/Gc5zzzckgDqZ55kdvLj3iV8F7oRsNPjWeiUU5bjeEZr7snz2iAmXhL1cNDdt5xSgX2873I7eVHeCW8RS1618QT/sorr9ymDf0LXdSQld7bOkhLjw2B0bLjuG27Xm/DuK+8Qxy8wxCB5Tcm8nBe5PbyI6wS3o1sdO4TT3h25ZkyZUroS4xZca+eG1LSGNDjez33+jDnO3a2ncYAf6fz8uM54XgWJ6djeB+lSaHT2kd5lt7HZ2qQBCCghPdRyHEiPD0dorF13DtPpOFbt+UsLxufXsONgBLeR/lEnfAsc9l1acRh5xgZsRXpxbri7nmfMbF1Xg0Ih1Zapw2IRSIcVyW8j3KIOuEZ+/od9/KtzjEu904NNAhOfNa5GxAaFmcDwpg73T3hnQ0I90zMWUde3BKJSiAWncyvSngfmEWR8OSZXxics7GhwXA2KPx3NiAQ3s6ok3eeMUtvHfdOCcV9z/tOPXv3PenhZx35cebP+sf1qoT3UbJRJDwKLE4i+fjMSAZxE9ZNaDfhuU/XYLgbEO6dDQgSi/Me6cfZgNB4OBuQsDS6tnCV8BaJNNcoEp5KF7bKlgbi0DxyNyCQ2UlodwMA+Z2agDQmzgbF694ZnvdpRKwjLacERDmSJ+ucjYn1y+SqhPeBVlQIT2XItkL4gEODZICAm7BuQrsbFBoAZwNDg+GU1Iq7d7/vTq9169ZywAEHZPAF0Qz63zT0NuQ/KoSnMlDg6uKLgJ8GxEoIS5YskRYtWkjz5s3NkealSpUyE6gdO3aML0D//2WJILyK8LGvxyk/kGPOpk2bJnfddZfZLMQeQ84KCacmdenSRUaOHCkLFy5MGUecHsSW8G6RME6Fpt+SGoH58+fLsGHDtjiGHHIzWYvYPnDgQDMXsG7dutSRxPhJrAnvnPSJcRkm9tO+//57mThxYtEx5GXKlDGiOdcTTzxRevbsaZ7rUeT/VZHYEV7F9/8KN07/1q5da3rmAQMGmJ66SpUqhtz03oceeqjp0enZdXI2fanHivBMzKEuqy76CDCmZmzNGJuxNsTmxxicjTsZk0+fPj3UR5GHsRRiRXhad6e6axgB1zxtjcDSpUuNodLNN98sTZs2NTv7QO7SpUubWXTO/3vmmWeE2XV12SEQecIjwqsYl10lKOTbGzZsMId3Dh48WM4//3ypXr16Ue990EEHmY05HnroIZk7d24hs5WYtCJPeJQvmIFVF04EFi1aJKNHj5Zu3brJ0UcfXUTuvfbaS8444wxBw+3VV1+VVatWhfMDYparyBOe8nCqWMasfCL1Ob/88os5xadPnz5GqWX33Xc3BC9RooQ0bNjQKD+NGzdOvvrqq0h9V5wyG0nCI8I7TUPjVCBR+ZaNGzfKrFmzZMiQIdKuXTupVatWUe/Nf/yGDh1qwmzatCkqnxX7fEaS8CjVYBqqS3CFq5/0ymPHjjW9dIMGDWSHHXYwBKcXR02VoRVn9K1YsaJwmdKUMkYgkoTP+Cv1hYwQYDw9depUM74+/fTTpWLFikW9d/369c14fMyYMfL5559nFK8GDh6ByBAeMZ4dYLRXz32lmTNnjjAzjnkqM+V2zbtGjRpmJv3ee+81M+t///137hPXGAuKQGQID9Gd5pAFRSlGibGWzZp29+7dt7AU41Qb1sB79epl1sSXLVsWo6/WT7EIhJ7wOgNviyrzq9tSrFKlSkW9N9prXbt2Ndpsn3zySeaR6xuRRCDUhMd+GfFSSe+vbjktxQ455JAicqOnwIEbWIqx0WVSLcX8oRjvUKEmPNDbTQviXQyZf53TUoy5DWspVrZs2SJLsUmTJolaimWObZzfCCXh0cxS9x8CxVmKderUSYYPH64qxv9Bpv9SIBA6wiO+M4GU5J7daSlWr169ItEcS7GWLVsWWYqtWbMmRbGqtyLgjUDoCE82kzRmd1qKNWnSRMqVK2cIjqVY48aNBUux8ePHJwoT76qqvrlAIBSEZ8ktCWvsTkux8847z9NS7OGHH1ZLsVzUbI3DE4HQEJ6dZeNm5lqcpVi/fv2Mpdjq1as9C0c9FYFcIxAKwuf6o4KID0uxl19+WaylWIUKFYxobi3FOBcOS7HFixcHkT1NUxEwCARGeMT48uXLR3KHGizFZs6caSzFLrzwQqlZs2bRxFrt2rWLLMVmz54taimmTAsTAoERHhBQlY2Cbry1FLvqqqsklaXY5MmTA7EUw3IQU2Gvn3Olw4br0KGDCZukidEwES7ovBSc8GEfp1tLsb59+4qXpdgVV1whYbIUY+NO5j/cPzQU7TbdPMOcmAaWH6fQIl2FvSyCJkcc0y844VHzpLcJi3NaitWpU6dINMdSrG3btoKl2HvvvSf//PNPWLJcbD7o2dFlsNKTV29OA6DHbxULZewCFJzwXpWvUKh+8803RZZijRo1kpIlSxqC09tZS7EXX3xRom4pRg9eHJn9hEFCYLkUaYHtv+0QgbjZHZgr2PFjUhKHBFG1alXjx/DBNjqFKmNNJz0CBSE8PXqhxUdrKXbnnXcaEdbLUmzUqFESN0sxGtTiDI4gK2Esgb2qCMRFGiMs4bjaxpohAiSnQcCPZ0gUEB2besqaH+8X1/B4pa1++UOgIIRHfMy3GI+l2KOPPmpOIElnKbZ+/fr8oRmCmCGc85x1myXwt701xEzXANMrp2sQ7JyAjZsrxIbgTkejQVh14UGgIITP9ee6LcV23nlnU0HdlmI//vhjrpMOdXy2d/ciM8/oqflBTnpkemYvRxgIn8pBYnfP7UVuL79Ucap/YRBIXao+0rc9weuvv75VaMZvuejVnZZirVq1ksqVK5vKSIXkTDFrKbZgwYKt8pA0D0jot0eFjPT0Xs4P4Xnf6bzI7eXnfEf/Fx6BvBEesm8L4bEUGzFihHTu3Fm8LMX69+9vzhRTS7EtKwuNL+PqVL32lqGlaNzt9uceCYEGNdWEG42KEt4LufD75ZTwVJBUlcQLCizFqKCcKaaWYl4I+feDgO4xtH3bTrbZe67M0vNL5YjLzry7wyjh3YhE5z6nhKcipBIpsRSbMWOGcKYYlmLVqlUrEs3r1q1rzhTDUmzevHnRQS9EOWVMnkqiordmWY1TV5m4Q5Qvbl9/O8vOe7zD1fbqSvgQFXyGWckp4akkdsLIWopdfvnlctRRRxWR254phqXYa6+9JmoplmGJeQRHqmLcnUq6ss8hLBKVLSOPqLbwcr5H/Nbxvltq4N4dr5efjUOvwSCQE8KzOSKWYr1795ZmzZqJWooFU5iaqiJQHAJZE56lMERGfliKtW/f3pwphqXY5s2bi0tfnysCikABEciK8OTznXfekQkTJsjKlSsLmG1NShFQBLYFgawJvy2J6juKgCIQDAJK+GBw11QVgUAQUMIHArsmqggEg4ASPhjcNVVFIBAElPCBwK6JKgLBIKCEDwZ3TVURCAQBJXwgsGuiikAwCCjhg8FdU1UEAkFACR8I7JqoIhAMAkr4YHDXVBWBQBBQwgcCuyaqCASDgBI+GNw1VUUgEASU8IHArokqAsEgoIQPBndNVREIBAElfCCwa6KKQDAIKOGDwV1TVQQCQeD/AKRahJPDI3GrAAAAAElFTkSuQmCC[/img]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAANoAAABVCAYAAAAv+/rWAAASZklEQVR4Ae2dCfRWwxvHU4iQ3aGyJQlZk5DtcCSOLY69bFmzljiF7MeeLdnKvkb2cLITUdmzRXaFbFkqsjz/85m/eU3zbve+d33f3zPnvOe+997Z7nfmO/PMzPPMNBN1ioAikDgCzRJPQRNQBBQBUaJpJVAEUkBAiZYCyJqEIqBE0zqgCKSAgBItBZA1CUVAiZbjOjBmzBhZf/315ayzzspxLjVrQRBQogVBKQM/Q4YMkWbNmhV+vXv3ls8//zyDnGiScSCgRIsDxRjjmDhxomy33XaGYKeffrq59u3bV7p27SodOnSQUaNGxZiaRpUWAkq0tJAOkM6wYcOkdevWsuaaa8rYsWNNCHq1M844w/zv37+/Id6AAQNk9uzZAWJUL3lBQImWg5JAJEQ0hFSHHXaYzJo1q5CrZ599Vj799NPC/ejRo6Vdu3bSvXt3ee655wrP9U++EVCiZVw+iIKIhEsssYTccsstgXLz9ddfy9577y0tWrSQCy+8MFAY9ZQtAkq0jPCfM2eOIALSi+20004yderU0Dm58sorpXnz5tKrVy957733QofXAOkhoERLD+tCSoh8iH6Q7IILLig8r+XP66+/LltuuaW0adNGbrrpplqi0DApIKBESwFkNwmI1bJlS+nSpYuMGzfOfVXy/9Zbbx2IQIMHDzbEPfLII2XGjBkl49KH2SGgREsJe0Q7RDx6seOPPz5wqvi3s47VArHAzXiPRe7HHnusmnd9nyICSrQUwEakY6ZwhRVWkHvvvTdUimGIRsS//PKLHHjggYbQrMP9/fffodJTz8kgoERLBlcT6/fffy9HHHGEqfR77bWXTJ8+PXRqYYlmExgxYoS0atVKtt9+e3n11VftY71mhIASLSHgH330USPCQRRmB2t1/jpamHjef/996dGjh1k6GD58eJig6jdmBJRoMQNKdFZPcYsttpDXXnstgRTCRYlSMoTv06fPPIvf4WJR31EQUKJFQc8LO2nSJNODUKmZBcyTe/rpp6Vz587SsWPH0OPEPH1HveZFiRZTyV111VWy7LLLSvv27QWxMY+OiRGm/2kIBg4cKD///HMes9mQeVKiRSxWV0/xoIMOkpkzZ0aMcd7gQdfR5g1V+e62226TpZdeWhBtVV+yMlZxvVWiRUDynnvuMZr2Cy64oIwcOTJCTOWD0vsEXUcrH0vxGxqIXXbZRRZYYAG56KKLij3ok1gRUKLVAOfvv/8uJ554ohHBmD7/4IMPaoglWJCkiGZTh2Sksccee8jkyZPtY73GjIASLSSgiFroFlI5zznnnJChw3tPmmjkaPz48cawlEX1oBYE4b+kaYdQooUof0xSMMxce+21hfWtNFyUdbSw+TvhhBNMA3LUUUfJtGnTwgZX/xUQUKJVAMe+Qk9x9913N5WwX79+MnfuXPuq4a6oiLVt21Y23HDDVGZP33jjDTnzzDNL4vjTTz/J5Zdfbt5z5b6S23XXXYX48uiUaFVKBT3F1VZbTRZffHG58847q/hujNeojqEyhtgKCRiTJuHAFlxJx3eQCuXolVde2UwGbbXVVua+Etkg2gMPPOBHlYv74i/MRbayz8QPP/xQWHPabbfd5Isvvsg+UynnANWx+eabT3r27Ckvv/xyrKmj+LzeeuvJZZddVpJoPIdkLrEgWxIzsLF+WJnIlGglgGHBuVu3bqYCDB06tISP9B4lsY4WJvdvvfWWWW9bcskl5eqrrw4TtKJfeh5IxBi0VI8GqXxzInrAVVZZpWy8hHFFR+7Zb4X1TXDkhwiahVOieahjWrLQQgvJRhttJBMmTPDepn+bxqxjkK8aNGiQIQQ90ZQpU4IECeSnHNEQKf0Jp3J+bUJg5YbhHrJBUJ5z5VkW4qUS7d9SwpSEvTsoCNST8uLIT17EJYxJGa926tQptv0ly5GH73ZJQ3nQW/HcFSfdcvLDcI8I6joaCr+ndN8n9V+JJiLoKVrDzAcffDAprGuKl8qSF6LxAWwqZA1LTzrpJGHiJIoLQzTrNwzRfLKCJb1c2q5JE40JDuR3KvO+++4budIkUXhUDL+yJJFO2DitYSmL908++WTY4AX/ljyFB//+iUt09LFTovlIJ3yPniLTx5DsmmuuSTi1xoyeLfLYvpzNhi6++GL5559/Qn9oOaIxVe+LeIyxmIks5yhLl1j+PeGUaOXQi/k5a0KIPExb0xqrfl90gK1h6Z577ilsfxfGlSOanWF0xUREPsTWcs4nln9POCVaOfRifP7888/Pc4BEjFE3+ajAFsPSFVdcUW644YbAeJQjGhGwzsZ0PovmSB+Iky7x/ER8Yvn3+Fei+ajFfI+eojXMfOKJJ2KOPbnoqGSuOJRcSvHEbDcjOvroo+Wzzz6rGinrXFT+co6ejffMHlYiGeHx555T4N/jByyJM23X8JMhbFDDRAet2yGHHFJ3p7CQ70oVMe0KEyQ9VNWWWmopsxaZt1ncIPlPwk9DE+3mm2+WtdZaSzDMrFfzj3okGhWVgzgwLLX5Z7/JpuwakmjoKR533HGmkDHM/Pjjj+u2jG1FrdcPYDaSb9hxxx3lhRdeqNfPiJzvhiMa2gvWMPP888+PDFDWESA21tMYrRReaN2g0sY+JVdccUUpLw3/rKGIdvbZZ5uZKQwzX3zxxYYvvHr7QGtYevDBB8s777xTb9mPlN+aicYMULVZIGaAqvmJlPt/A9NisucFIsoxxxwTR5QaR0IIPPTQQ+aIKY4Pvv322xNKJX/RhiIapGG6mdMpqdT8WOfwtaFR/uS59YN5gks43rPqz881a6gFHrQ6rGFm2AMkaklPw0RHgIkRa1jKJkdMnDS6C000nxysb7CQaNcvIBREtCv43LPwaO8B1FWtcf+HARs9Rbtmg2FmoxZWva2jhSlD7NvQ0KEhbvRjpkIRrRyI9Fx2wM5iIMRzHe/wA+nowdwekP9hezV6rk022cTE2eiDa3Crt3U0t+yr/Wedc/PNNzc2gOedd5788ccf1YLU5fvIRIMkVAbbo1EpSpkhuGSkF4N0/ML0aBTCaaedVjDMDKtXV48l1OhEs2Vy6qmnmnqEvuQrr7xiHzfMtSaiQS72N8QsHDHRVWmBZKVaYCqM9QfB8MOP/0EcunTWMBOl4KbimgrRKM+nnnrKjLfR0L/22msbqohrIhq9EISiEiBfu6JgOaKVex4ETQiNsuryyy+fyhZoQfKUlh8aIyuWp5VmlulwEIe1EeRAjo8++ijL7MSWdk1Ec1OnErhGeqXsiPAPKV1CunGU+89W2xZ09BX19JNySDXec1TmFl54YbODMraD9e4iEw0A6K3sWIsWmHvfQbQwLfMdd9whG2ywgSHo9ddf70en900AAWaWMSyl7pxyyimCal29uliIxvQ9BMPRazFucx3PACvIeOzHH38sGGZyrFCSB0i4edT/+UWA2Ujqzw477CAcqFiPLhTRIAwa8XaGkSvrPIiO7hQ9xEPk4z3PMdqzPV4lkMaOHVtowdj2TZ0YfMNIAo2KGRu4olq3zDLLyCWXXFJ3nxmKaBQ4JKJ1sT/GZH5FgGCIj9YPJKvWm2GYudxyy8mqq65aFF/doRpjhsHQSgsxRlu3UWFQCia9e/eep3HP+weFIloSH8Nh6vvtt58BD8PMP//8M4lk6jZOJVpx0Y0ePVrYOZkezi4ZFfvK15NMiXbjjTeaw8s5dZLjXpuae/vtt6XaT4lWulYwMYLqHfhge8gJpnl2mRDtyy+/LBhmIoped911ecaoYt4Qk91zoBGR3Xs7jrWRIGYzrp00aZIce+yxZjaNI6FoaPgxu+beY7jKeNc6P75q96Tnbifg58+/t+nUyxUVPMiGDSKWAXl1qRPt4YcfLozfMMxkp9tLL71Uvvrqq8QwcseH/Hcrnq34NnEmb1iEt473FKR1jJcq3fv+/XsbHqKxPoTo4y6H+Pfkx31f7b5cejb/KIG7+ff9+/fk102f/Ln4lCK629DYdJO8IhV07dpVWrVqZRqx3377Lcnkaor7vxpUU/DggdBT5ChaZijZx8PVZ0Pm5hfUUdms8wvaJwr3VCxLNr8i+RWX+NzJB/+eeIjDOt67+bHPq10t0ar5S/q9/z3+Pd/qjoO4d4nHTLR7D3buJqfViAp2zGTH4U4++WRT1oiU48aNiyPK2OJIhWhMzVrDTGaNfGd7NchIQbstIgVBC2orMxUb4nDF+QVviUE81uHHvbfPs7zmhWhJY+A3RJSFazIFERk+WMcMNTPZ1kFy96AK4qtUlo8//rgxLMUectiwYTaazK+JEw3DzA4dOpizn22v5QMFkdDKnzhxoiGO2wNBMMC3xAKxPBInbEkGJVoj26OVwozydssaorlrsH4Pyb3b4xInu1Hvv//+pkFmJpujkbN2iRENZVCUQiFN9+7dCz0SQPIMslhHiwUhR40aVbG1sv4b4RqUaGBFZVL3fwT8HpLez+3xIKXtMUeOHGnqGudxo9KXpUuEaGwxxjiMSoLmPTK8C0apHundd9+V4cOHZ4lFqmkr0ZKBmzEjP+uog0hUXDGv+uabb+yrVK+xEm3mzJlGBGzRooXRd+RY1qDur7/+Mqo1tZxIEjSNPPlToqVTGjTq9IL2II75558/kwY9NqKx1rPzzjubloP1oVocg9eoB9vVkm4WYYISDbHRFbOzyGujpMm+JJy/gL4kS0tz585N7dNiIdpdd91lzsiitVhnnXXmmSW0X4LszKSH/dlZRPc9W5Cxf4Q7y+i+t2Hz8N7my17dvPHfd/57n2j+ez+83seHwOGHH14QJeOLtXJMsRCNJDCNYTdaWmB+7swR75kZsu8a4b0Pq/tt/Pdd1Pd+fHpfOwIvvfSSIRpHKqflYiMax6t26dJFttlmG8FQs6kfapBWAWo6wREYP368Uf3DSmTgwIHBA8bgMzai2byw7tOtWzejHYApw9ChQ80Yg4kSdYpAmgiwlR1HSDHb2KNHD7OpLztZh5mkiyu/sRPNZgwVK0i32WabGR00plfXWGMNoyEyePBgQXOf/fFnzJhhg+hVEQiNwOzZsw1x7rvvPsGm8dBDDzVjfFT97NR+nz59jF7pnDlzQscfV4DEiOZmkA9E6wNysYi98cYbG51HgOCHbRHP2NOvf//+RskYhVu6ejT91TVdBNAiogcaM2aMUWrAugHiMHnUtm1bU39sPWrfvr2Z+UanFv9BThxNC9lUiFbuY6ZPn27ESvbwg2CcoUWvx8GBFjx7bdeunWy66abGhKRfv37CyTGMBbEGgMRs5JLmdG25b9LnwRBgbxhUo5555hkj3mHBgVLwAQccYMQ8FB4WW2yxonrAloPsUg3Zzj33XKOMPnny5NyXfaZEq1QkmM2ggX3rrbcaUnHUD60Yywdt2rQxywmWhO6VM7iwvN12222NuTuDXjZ3YY0OLfH7779fmLhBtEUbBYIyfmQ/QXXhEMAchTMPPvzwQ8FSHmXwRx55xBAHG0P29mD4wBkJqErZsXvLli2LCMQe/KxxderUyajs7bPPPjJo0CDTi6EozHgrS9EvHDLFvnNLtOKsFj/59ddfjXhAIUOeu+++26z609uxbsdkDDsnUcCrr766Wahs3rx5USFboi6yyCJmk1b8MoMKsXv27GkseSl4FuURfTnni0pAJWLh0+pqsoTBmiIqQFQOFpppLLBeoNdlC3NspyD4lClTzEmkiDc0KqgGsViPqMR3UanoodGUQWsGy4ZZs2aZvS2xLmZsi0RAQ8FSCrqlVEbOHXvzzTeFo6xoTJjKZpdn8IEEnFuAgemIESNM44O6HHixJfeAAQMEaQFFXLaXwAAVKYOZZER71jmRLBj/VMORDW/XXXddgyGWG6xdIfYxOUaDR14YGkDSet5GrrhWln5S10Qr/UnVn9KDffLJJ6YyUgFRZkZ8pedjhqpv377Sq1cvU0lYQEdUYY2Q3bw6d+5sWl305zDFoOIhzqBtwFrioosuas4GYPHeEjgPV4iBSI5xZOvWrc1h7kxzIx2stNJKwvimY8eORkcVgqCIC7mYzMJ6mQYL8jFrN2TIENO4QBhEdya1aDzo3dCcV1eMQJMkWjEMyT1hsyEqH2IWBKf1/vbbb2XatGlmnwsIT6vOeIWxBhozaI3QG1GBEcc4+5nWf8KECUZEY3KAis2el1OnTjW9OpNGVPTvvvtOGP+wjsmMHL2iisXJlW/QmJVoQZFSf4pABASUaBHA06CKQFAElGhBkVJ/ikAEBJRoEcDToIpAUASUaEGRUn+KQAQElGgRwNOgikBQBJRoQZFSf4pABAT+BwYnYsxAPZ0TAAAAAElFTkSuQmCC[/img]
[size=150]For a sphere with radius [math]r[/math], its volume is [math]\frac{4}{3}\pi r^3[/math] and its surface area is [math]4\pi r^2[/math]. Here is a half-sphere bowl pressed out of a piece of sheet metal with area 1 square foot. [/size][br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAKMAAABqCAYAAADQi+H8AAAPHUlEQVR4Ae2de4hVVRTG1SwF03ziQJlEIhrmaxTREjVQyzJ8opWaCr5NMy2RpEIDQy0rLCkn35riH0EoGuSTmCzf4gOVUclXpZkRka9Y8duw7cw099xz7j3n3HPvWQuGe2f2OXuv9a1vzmPvtdeqIiqKQEwQqBITPVQNRUCUjEqC2CCgZIyNK1QRJaODA7/++qscPnxY9uzZIzt37pQtW7bIV199JevWrZMvvvhCPvnkE1m4cKG8++678uabb8r06dNl4sSJMnr0aHnhhRfMD9/5G22zZ882x77//vvm3GXLlsmXX35p+ty6dasZ44cffpAjR44IYyddEkHGP//8U06ePCk7duyQNWvWyPz58+XVV1+VwYMHyxNPPCGPPPKI3HfffVKlSpVKf6pXry7333+/NGrUSJo0aSLNmzeX1q1bS6dOnaRbt27y9NNPS79+/cwP3/kbbRzDsZzDufRBX6nGQQd0QSd0Q0d0Reft27cbG7ClUKWgyHj06FFzFZs1a5Y899xz0rJlS3nggQfKOf/ee++Vpk2bSufOnWXQoEEyZcoUee+992TVqlXy7bffyokTJ+TcuXPyyy+/yB9//CG3bt0K3Pf0Sd+MwViMydjogC7ohG7oiK7o7CRw3bp15bHHHjM2YitXW2zPd8lLMuJEnPfBBx/IqFGjpEOHDuWubI8//ri8+OKL8vbbb8tnn30mmzZtkgMHDsjPP/+ct/5Cd2zAFmzCNmzEVkvUGjVqGCzAZNGiRQYjsMoXyQsybtu2TbgCPPPMM/LQQw/dBb9x48bSs2dPee2112T58uWyf//+UK5kcXcmV1psBwOwABOwsSQFM7ADQ7CMq8SSjMePH5ePP/5Ynn/+ealVq5YBtUWLFjJs2DDzDMWLxYULF+KKaWz0AiOw4rkT7MAQgoIp2ILxsWPHYqNvLMh47do12bhxo4wbN04effRRAxjPegMHDpRPP/1UTp06FRvA8l0RsARTsLXP02AO9vgAX+RKckZGpjIWLFggTz755N3bSZcuXeStt96SXbt25QqPxI0L1mAO9va2jk/wzZUrVyLFI3Iy8swyYsQIY3jt2rVlzJgxsmHDBrl69Wqkhutg/0cAH+ALfIJvICe+iuo5MxIy/v777/Lhhx9K27ZtjYH8F37++edy8+bN/yOif4kFAvgGH9krJr7Dh9evXw9Nv1DJuHv3brM6Ua1aNalZs6aMHz9evv/++9CM0Y7DQQCf8UyJD++55x7jU3wbtIRCRiZxBwwYYK6CHTt2NEthf/31V9C6a38pEDh79qx0795dDh48aD653XJ3ylbwIUui+JQ++/fvbybss+3Xnh84GefOnWsULS4ulm+++caOo58RIsB6OrfVNm3amHVwlkGDFnyLjyElPg9CAiPj5s2bjfFVq1aVefPmBaGb9pEhAlOnTjXTNlwhwxZ8jc8hPxzIRrIm46VLl8ySHP8hLO6fPn06G3303AAQIFDj5ZdfDqAnb13gc3wPB4haunz5srcTKxyVFRl//PFHYdGeSVOmBFTigQCkCOPWnM46OAAX6tSpI4TG+ZWMychLCmueffr0kX/++cfvuHp8SAjw0gIZcyVwAU48+OCDwrKuH8lI6/Pnz5vwrK5du8qNGzf8jKfHhowA0Tq8uORS4ATcYC0crngV32Rk0pNX+3bt2kW+XOTVqCQfx7NilM+LqbBmKRGOwBWvE+W+yfjUU09Js2bN5MyZM6n00L/nEAFu01G8RXsxEY7AFTjjRXyRcf369eZ5hD0bKoqAFwTgCs+wcCed+CIji+ZeWZ5uYG1PDgI9evQwARfpLPZFxoYNG5rQonSdarsi4ESAcDS4k048k5HdaVxu4xQZnM44bY8HAnAG7sAhN/FMxtdff93sSHPrLOltrELYnyFDhpSDg30qto3P4cOHl2snCMHZzkqGU3gjdbYTReMU3l6d7ZMnT3Y2CytlzvZp06aVa2eXorP9jTfeKNduV1nsMewbdwpziraNz3feecfZbCbC4ZCbeCYjWyMJuFRJjYDTGUrG8mRkvzgcchPPZOzbt6/ept2Q1LaUCNjbNBxyE89k5BILu3kYVVEE/CAAZ+BOYLfpOXPmmLAkXtNVFAE/CDAdyE5EOOQmnq+MrHnWr1/f3Kp10tsNUm1zImAnveEOHHITz2QsKSkxb0S6HOgGp7Y5EXAuBxJWBofcxDMZiVUjolcDJdzg1DaLQMVACbiTLubVMxlJk8HEJXtrCQsiPEhDyCz0+ulEwIaQkQUOrsAZuAOH3MQzGcvKykyHpaWlpj8mOQmg1OBaN3iT12aDawm8JgAbgTOQEQ65iWcy0gn7ZlesWHG3P0LLeRbQbQd3IUn0F7vtgK0obEmxQnY0uJNOfJGRTKykVXMKm29YuoL5rEDohiwnOsn4bpcK4QC5IVl6dAqcgTvpxBcZIRvZqyoTtimyXVG3qlaGTuH+zW5VZatDqq2qcAbupBNfZGRxvFWrVq596iZ+V3gKptHPJn44UzGwojIgfJFx5cqVJl1xZR05/8aDK6kvuGxrehMnMvn9vWJ6E1LY2JcUN8tInA930okvMlKSAoJ5UYCBbeInkgXxAEvYkyZ+SueS+LXjM5J24UOSePGO4DXxE1yBM3AnnfgiI52RgnfJkiXp+i3XzkS5psQrB0nsf0mVEs9vAim4Ame8iG8yPvvsszJ06FAvfVd6jCYLrRSWWPwxjGShcAXOeBHfZCRZeVFRkZe+XY9huYjQIk2j7ApT6I1uaZSDqNoFV+CMF/FNRia6eQY4dOiQl/49HaMJ5j3BFMhBUSaYhyNwxTkB7maEbzLSGeFAPAOGJUQGa+mN7NH1UnrDbz4cP1rBkQYNGng+JSMyMm3DT1TCc6YWJUqNdlyLEsERpn+8SkZk/Oijj8zmrDt37ngdJ9DjbLk2gjVtuTZKlXFL4Cep5dqYz6N0HZhQyo6Sdrkq1wY32MDHHc6rZERG1h5x+tq1a72OE8lxFHOkqCNXUQpZshuNRXtLUj4LoZAlIfyEZ2EjtlKCOG6FLOEGeF+8eNGz7zMiI71T7ivdbi/PWoR8oC3xyybyfC3xS/JPyhTnS4lfuAFH/EjGZMyE+X4Uy8WxTGWwZ4MZA4qfU6DcFj+ncHmq4ufcFm3xc77b4uesx1IonYLpnEsBda5i9EmgKWOwMkHB9SCmUXKBWWVjcjXM5M6ZMRkJouSZgCrzKoqAEwE4QZyr34zGGZORwSnrRSCEiiLgRABOwA2/khUZmXLhckytYxVFAATgApzIpN5gVmRkcCJ4KyYpUrckFwG44CWquzKEsiYjD+X8J/Cmp5JsBFhqhAtwIhPJmowM2rx5c5k0aVIm4+s5BYQAHIALmUogZFy8eLH5j/jpp58y1UPPy3ME8D1XRbiQqQRCRgZ/+OGHZcaMGZnqoeflOQL4Hg5kI4GRkYldltqIU1RJFgL4HN/DgWwkMDLevn1bGjduLFT0VEkWAvgc38OBbCQwMqLE0qVLzXPDd999l41Oem4eIYCveVbE99lKoGREmV69epnq79kqpufnBwLdu3c3Pg9C28DJSIg5/ykEBqgUNgL4GF973VaQDo3AyciA5G6uV69eQUWipAMyae1EGeHjdHm6/eASChnZc9u0aVMZO3asH1302DxCAN/iY3wdlIRCRpRbvXp1YA+2QRmr/QSDgH1RJVA5SAmNjCg5c+ZMQ8hMIjiCNFL7Cg4BG6mFb4OWUMmIsqRCI8NtXGogBw1gkvrDh/jSS3q7THAJnYx///23tG/f3uT/zkRBPSc+CJDDvbi4WPBpGBI6GVGaTfns0hs5cmQYNmifESCA7/AhvgxLIiEjyn/99dfm+TFdlaSwDNV+M0cAnzGfiA/DlMjIiBGku8CooN/CwgQo6X3jK3wWZjobi3GkZGTQV155xSSc1KSh1gXx/cRHJAedMmVKJEpGTkasIl9fs2bNcpZ6IxJk83wQ0qLgI7JWRCU5IeNvv/1m0nP07t07Kjt1HJ8I4BtSqJCuMCrJCRkxbu/evSZZ/YQJE6KyVcfxiAA+IZHWvn37PJ4RzGE5IyPqb9y40RjNf2GusmUFA2Nh9IIP8AXZzPBN1JJTMmIs/33cDng+0ZeaqN3/33hgjw/wBXetXEjOyYjRPJfwoMybm077RE8DMAd7Xix5ns+VxIKM1nimEJjT0olxi0j4n3ZCmym3XEusyAgYdmJclw7DpwYYRzWh7cWa2JERpVl2Yh2UhXmN9vHiRn/HgCnYgnHYS3x+NIslGTGABXkiRAhZ0nhIPy51PxYswZRIqjCDHty1qLw1tmREXUKViJ3jVhLEVsjKIUjOX22ENpiGFQaWDZqxJqM1zEaMs++ikNINW/vC/gQzsOOfOowI7aD0zwsyYizTD2wAYkeaboP17n6wAjOwY19SnCVvyAiI7ERjayT/4Wwe18wVqakFNmAEVmAW5C6+1KNm15JXZLSmsmmczBUATZ4XTTZlkRGDBZiADRgFtcH+vxHC+5aXZLRw8EBOwiEyYJGSLcn5IbEdDMACTPLxhS+vyQgpyXxFKjZyA3I1IHsq6XyTIqSvxmZsBwOwoJZgPkrek9EJOllTSeOLY0h0XshVGLANG7EVm7PJGOvEMJffC4qMFkgSnJNxH0dRk4QiOX5q2Nl+4vaJDdiCTdiGjZkmc4+bbehTkGS0QLPaQHEcqjXhPOrZUWYuV9VgrV5+PtEVndEdG6hKhk2FuCpV0GS0TqdsGA6lsKJ1KLWQCcqgWnzcBJ3QDR0hHzqjOzb4LYEWN9vc9EkEGZ0AcKujBjJFuakSj6OLiopk6NChsmTJEjlx4oTz8Ei+MyZjowO6oFP9+vUNGantTUnlJEjiyFjRqczDzZ8/3wSW1qpVyxCBsPtWrVrJwIEDTT3n5cuXS2lpqVy9erXi6Z5/51z6WLFihemTvhmDsSAfYxPcii5UdU2iJJ6MFZ1Oyd2VK1cK5XkJKOAloWbNmoYwkKZq1armGZTIlxYtWpiXiR49epjbKLdSvnfo0MG0cQzPq5zDufzQF33SN2MwFmOqFPgLTJAOLisrMzWiN2zYICUlJbJo0SITkc5S2/jx4+Wll14yP3znb0RQcwzHcg71pelDJTUCemVMjY22RIyAkjFiwHW41AgoGVNjoy0RI6BkjBhwHS41Av8C6PnYPCATPjMAAAAASUVORK5CYII=[/img][br]What is the volume of the bowl?
Suppose this two-dimensional figure is rotated 360 degrees using the vertical axis shown. Each small square on the grid represents 1 square inch. Draw the solid that would be traced out. Label the dimensions of the solid.
Find the volume of the solid. Round your answer to the nearest tenth if needed.[br]
IM Geo.5.15 Practice: Putting All the Solids Together
[size=150]A right cone has a base with diameter 10 units. The volume of the cone is [math]100\pi[/math] cubic units. What is the length of a segment drawn from the apex to the edge of the circular base?[/size]
[size=150]A right pyramid has a square base with sides of length 10 units. Each segment connecting the apex to a midpoint of a side of the base has length 13 units. What is the volume of the pyramid?[/size]
For each pair of solids, determine if their volumes are the same or different. If the volumes are different, identify the solid with the greatest volume. Explain your reasoning.
A prism and a pyramid have the same height. The pyramid’s base has 3 times the area of the prism's base.
A pyramid and a cylinder have bases with the same area. The cylinder’s height is 3 times that of the pyramid.
A cone and a cylinder have the same height. The cone’s radius is 3 times the length of the cylinder’s radius.
[size=150]A pyramid has a height of 8 inches and a volume of 120 cubic inches. Determine 2 possible shapes, with dimensions, for the base. [br][/size]
[size=150]A toy company packages modeling clay in the shape of a rectangular prism. This prism has dimensions 6 inches by 1 inch by [math]\frac{1}{2}[/math] inch. They want to change the shape to a rectangular pyramid that uses the same amount of clay. Determine 2 sets of possible dimensions for the pyramid.[/size]
[size=150]These 3 congruent square pyramids can be assembled into a cube with side length 2 feet. What is the volume of each pyramid?[/size][br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAArUAAACtCAYAAACuuoeeAAAgAElEQVR4Ae2dS4hkVxmAexeQ0WlBMIjSg0SUYEgvhBlDsGehJCgyDUqSMcEeXEgWgW5BQdBkEh95IGGyi0OEmUFQxIROJmriqkUQFyOORDBolJEOCZKFs3AR0MWRvzq3Xl237jn3nsd/zvkKmq66de55fP/55v+n+lbViuEGAQhAAAIQgAAEIACBzAmsZD5/pg8BCEAAAhCAAAQgAAFDUcsmgAAEIAABCEAAAhDIngBFbfYhZAEQgAAEIAABCEAAAhS17AEIQAACEIAABCAAgewJUNRmH0IWAAEIQAACEIAABCBAUcsegAAEIAABCEAAAhDIngBFbfYhZAEQgAAEIAABCEAAAhS17AEIQAACEIAABCAAgewJUNRmH0IWAAEIQAACEIAABCBgXdQ+9NBD5o477jD7+/tQgwAEMiCAsxkEiSlCYI4A3s4B4SEEHAhYFbWbm5tmZWVl/LOzs0Nx6wCZphCITQBnYxNnPAgMJ4C3wxnSQ90ErIrar371q+OCluK27g3D6vMggLN5xIlZQmCaAN5O0+A+BNwJOBW1J06coLh1Z8wZEIhOoEmOOBsdPQNCoDcBvO2NjhMhMCLgVNSeP3/ePPjgg+PCdj5hclkCuwoCOgg0yRFndcSDWUDAhgDe2lCiDQTaCTgXtdLVdGH78MMPm9OnT48LXbk8geK2HTjPQCAGgenkKOPhbAzqjAGBYQTwdhg/zoZAr6J2b2/PHD9+fFzIXrp0yVy5coXilv0EASUE5pMjzioJDNOAwBICeLsEDk9BwIKAc1F7/fp1c/To0VFB++Uvf3mmsJXxKG4tqNMEAoEJTCdHnA0Mm+4h4IkA3noCSTfVEnAuaoXUuXPnRj9yf/rPmvKKbXOjuG1I8BsC8QlMJ0cZHWfjx4ARIeBKAG9didEeArMEehW1s120F7bSjuJ2nhaPIRCewHxynB+x7T+j0g5n52nxGAJxCOBtHM6MUi4BL0Wt4FmWJOV5EmW5m4iV6SPQlRxlxjirL27MqG4CeFt3/Fn9cAKDi9pr166Z3d3d0Uy6kqQ0orgdHjR6gEAXgWXJEWe76PE8BNIQwNs03Bm1HAKDilp5A0rzDWOSKOVmU9hKO4rbcjYRK9FHoC054qy+WDEjCDQE8LYhwW8I9CMwqKiVIbe2tkY/kiybm21hK+0pbhtq/IaAPwJtyVFGwFl/nOkJAj4J4K1PmvRVI4HBRW0bNJfCVvqguG0jyXEIuBNYlhzbesPZNjIch0AcAngbhzOjlEsgWFEryFyTpJxDcVvuZmNl8Qj0SY4yO5yNFyNGgsA8AbydJ8JjCLgR8FrUyiUIV69enZlBnyQpHVDczmDkAQScCNgmR5x1wkpjCAQlgLdB8dJ5BQS8FbWSHI8dO2ZWV1fN9PW1wrBvYSvnUtxWsAtZoncCNskRZ71jp0MIDCKAt4PwcTIEjLeiVlhubGyMfppPQpjmO6SwlX4obqdpch8CywnYJEfpAWeXc+RZCMQkgLcxaTNWiQS8FrWLitlpaEMLW+mL4naaKPchsJiAbXLE2cX8OAqBFATwNgV1xiyJgNei1gaMj8JWxqG4taFNm1oJ2CZHGz44a0OJNhAYTgBvhzOkh7oJBC1q214F8pUkJXQUt3VvYFa/mEDf5Iizi3lyFAIxCOBtDMqMUTKBIEWtJMaTJ0+a9fX1VnY+C1sZhOK2FTVPVEjANTnibIWbhCWrI4C36kLChDIjEKSoFQZra2vm6NGjpu2VH2nju7CVPiluM9uBTDcIAdfkKJPA2SChoFMIWBPAW2tUNITAQgLBilr5vNr5j/ZaNIMQha2MQ3G7iDbHaiHQJznibC27g3VqJYC3WiPDvHIhEKyodQEQqrCVOVDcukSCtqUQ6JMcXdaOsy60aAsBOwJ4a8eJVhBoI6CiqJXJhUyS0j/FbdsW4HiJBEInR2GGsyXuHNaUkgDepqTP2CUQCF7UyiUIZ86cMZubm528QidJmQDFbWcYaFAAgSHJEWcL2AAsIUsCeJtl2Ji0IgJRilp5w9jKysrSN401TGIUtjIWxW1DnN8lEhiaHHG2xF3BmrQTwFvtEWJ+2gkEL2oFwO7urlVB28CKVdjKeBS3DXV+l0RgSHIUDjhb0m5gLbkQwNtcIsU8tRKIUtT2WXzMwlbmR3HbJ0qco5XA0OTYZ10424ca50BgQgBvJyy4B4E+BNQWtbKY2ElSxqS47bONOEcbgRTJURjgrLadwHxyIoC3O2Z/fz+nkDFXZQSiF7VPPfWUOXfunDWGFElSJkdxax0iGiok4DM54qzCADOlIgng7cro/Tc7OxS3RW7wCIuKWtTKh7vLG8Zs3zTWrD9VYSvjU9w2UeB3TgR8JUeczSnqzDV3Anh7elwjSJ1AcZv7jo4//6hFrSzv7NmzZm9vz3mlKQtbmSzFrXPIOCEhAV/JUZaAswkDydBVEcBbcm1VGz7AYqMXtUPWkLqwlblT3A6JIOfGIuAzOQ6ZM84Ooce5tRHA20nEybUTFtyzJ5BVUSvL0pAkZR4IZ7/JaBmfgJbkKCvH2fjxZ8Q8CeDt4biRaw8z4Ug7gaRFrVyGkOOlCNM4EW6aBve1EAiVHHFWS4SZR4kE8LY9quTadjY8MyGQrKiV5CgXgq+urhr5Wk7Xm5ZXf5p5I1xDgt8aCIRIjjirIbLMoWQCeNsdXXJtN6OaWyQragX6qVOnRm9C6RsAbYWtrAPh+kaT83wSCJEcZX446zNK9AWBWQJ4O8tj2SNy7TI69T6XtKj1gV1jYSvrQjgf0aWPvgRCJce+85k+D2enaXAfAhMCeDthYXuPXGtLqo522Re1EiatSVLmhnB1iKRtlZqTI85q2y3MRwsBvO0fCXJtf3YlnammqL127ZqRD3rve9Nc2MqaEK5vZDmvD4EYyRFn+0SGcyDQTgBv29nYPkOutSVVZjsVRW3zBpT19fVBlLUXtrI4hBsUYk62JBA6OeIsX+NpuRVp5kAAbx1gdTQl13YAKvRpFUWtsF1bWzNbW1u9PglhOjY5FLYyX4Sbjhr3fRMInRxlvjjL13j63re194e3/ncAudY/U809qilq+3ysVxvYXApbmT/CtUWR40MIxEiOOLsy/p56vqN+yG7l3IYA3jYk/P8m1/pnqrFHNUWtbzg5FbaydoTzvQPq7i9GcvRNGGd9E6W/3AjgbfiIkWvDM045gsqiVl4B8vEqUG5JUjYCwqXUoZyxYydHnD09ftVWvlSGV27LcSnmSvA2Hm1ybTzWMUdSV9TKG1COHTtmNjc3vXDIsbCVhSOcl/BX20nM5IizB9sMZ6vVzdvC8dYbSuuO8NYaVRYN1RW18orP0aNHzcbGhpdXayUKuRa2MneEy8IjdZOMmRxxdjb8ODvLg0f2BPDWnpXvlnjrm2ia/tQVtYJhyOfVtmHMubCVNSFcW2Q5vohAzOQo4+Ps4Sjg7GEmHFlOAG+X84nxLN7GoBxuDJVFbajl5l7YCheEC7U7yuo3dnIMRQ9nQ5GlX40E8FZPVMi1emLhMpOqiloBU0KSlHUgnMs2r69tKckRZ+vbuzWvGG/1RZ9cqy8my2akuqiVP2mePHnSnD17dtkanJ8rpbCVhSOcc/irOCFVcsTZ7u2Fs92Mam2Bt3ojj7d6YzM9M/VFrXw8jrxxzPetpMJW2CCc7x2Sd38pkyPO2u0dnLXjVFMrvNUfbbzVHSPVRa2g293d9fYpCPOhKK2wlfUh3HyU63ycKjkKbZx123M468ar5NZ4m0908VZnrNQXtaGxlVjYCjOEC71zdPefMjmGJoOzoQnTfyoCeJuKfP9xybX92YU4s/qiVqCWmiRlbQgXQhv9fZacHHFW//5jhv0I4G0/bhrOItdqiIIx2RS18gHv8tWTFy5cCEKu5MJWgCFckG2jtlMNyRFnh20PnB3GL8ez8TbHqM3OGW9necR+lE1RK9fpyRtQVldXgzEqvbAVcAgXbPuo6lhDcsRZP1sCZ/1wzKEXvM0hSnZzxFs7Tr5bZVPUysK3t7fNtWvXfDOY6a+GwlYWjHAzYS/ugYbkKFBx1t/Wwll/LLX2hLdaI9N/Xnjbn12fM7MqavsssM85tRS2wgbh+uwQ/edoSY6xSOHsjtnf34+Fm3ECEcDbQGAVdEuujRMEitoWzjUlSUGAcC0bIdPDtSVHCRPOrozed0Bxm6m0xhi8vZRv8CxnTq61BNWzWbZF7cWLF83e3l7PZdudVluSFCoIZ7c3tLfSmBxxNsyuwdkwXFP0ircr5tKl8gtb2Vt4G8awLIvac+fOjd40tr6+HobKVK81FrYIN7UBMr2rLTnibPiNRJIMzzj0CHi7MsrttRS2sp/w1q9VWRa1gmBjY2P0zUV+cSzurdbCVmgg3OI9of2otuQovHA2zq7B2TicQ4yCtw+Oilr5pKOaClvZS3jrx6hsi1o/y7fvpebCFuHs94mWlhqTY2w2OHvFnD59elwkSKEgn/XNNbexd6L9eHhb37Xx87uD4naeiNtjiloHXrUnSUGFcA4bJmFTkuMBfJzF2YQaOg+Nt3jbbBpybUPC7XcRRa28YSz059c2WEmSByQQrtkROn9rT444G3/f4Gx85q4j4u2EGLn2gAXeTvaEzb3si9rmDSibm5s26/XSBtkmGBFuwkLTPc3JEWfT7hScTct/2eh4O0uHXDvhgbcTFsvuZV/UyvfLr62tmbNnzy5bp/fnkG0WKcLN8kj9SHNyxNnUu+NgfJzVEYfpWeDtNI2D++TaWSZ4O8tj/lH2Ra0sSJJkihuyHaaOcIeZpDiiOTkKD5xNsSsWj4mzi7mkOIq3i6mTaw9zwdvDTORIEUXt4qXFOYpsizn/4Q9/MF/60pd45/ViPMGPak+OwQEsGQBnF8PB2cVcYh7F23baeLuYDd7OcimuqJU3jMV+FQjZZjfV9COEm6YR735OyRFn4+0Lm5Fw1oZSmDZ4u5wrubadD94esCmqqL1w4YJZXV2Nfn2toES2dtnkGYRbzsf3s7kkR5z1HXl//eGsP5a2PeFtNyly7XJGtXtbVFF79erV0Z+7t7a2lkc90LPI1g22duG6CflpkUtyxFk/8Q7ZC86GpDvbN97O8mh7RK5tIzM5Xqu3RRW1Es5Yn1c72Tqz95Btlkfbo1qFa+Ph+3guyVHWjbO+ox+mP5wNw3W6V7ydprH8Prl2OZ/m2dq8La6obQKZ8jey2dOvTTh7MsNa5pQch63Uz9k4a88RZ+1ZubbEWzdieGvPqxZvKWrt94RTS2RzwsU1t264OluTHDsRHWqAs4eQLD1QS5JcCsHzk3jrDhRv3ZiV7m2xRe3u7q45duyYkTeipLohmzv5RcJtb2+b/f19984qPiPH5IizeW5YnPUXN7ztx5Jc686tVG+LLmpXVlbMxsaGe7Q9noFs/WCWKlw/Gu5n5ZoccdY91lrOwNnhkcDb/gzJtf3YleZtsUWthFde+dFwQ7b+UShNuP4k3M7MMTnKCnHWLc4aW+Ns/6jgbX92cia5tj+/UrwtuqjtH17/ZyLbMKalCDeMgv3ZuSZH+xWGb4mzwxjjrDs/vHVnNn8G3s4TcXucu7cUtW7xHtQa2QbhG52cu3DDCdj1QHK049TVCme7CHU/j7PdjJoWeNuQGPYbb4fxk7Nz9baKolY+B/PkyZNmb29veKQH9oBsAwG+c3quwvlZfXcvuSdHnO2OcW4tcLY7Ynjbzci2BbnWltTydrl5W0VRe/bs2dE3jaV+01izdZCtITH8d27CDV+xXQ+5J0ectYtzjq1wtj1qeNvOps8z5No+1Bafk4u3VRS1EiJJktevX18crQRHkc0v9FyE87vq9t5yT46yMpxtj28Jz+Ds4Sji7WEmQ4+Qa4cSnD1fu7fVFLWzYdHxCNn8x0G7cP5XvLjHEpLj4pWlPYqz/vnj7IQp3k5Y+LyHtz5pHvSl1VuKWv+xduoR2ZxwWTfWKpz1AgY2JDkOBLjkdJxdAmfAU7U7K+jwdsAG6jgVbzsA9Xxam7fVFbVyCcLOzo6RN6JouSFbuEhoEy7cSmd7Lik54uxsbEt/VKuzEle8Dbu7ybXh+Grxtrqidmtra/Smsc3NzXDR7dEzsvWA5nCKFuEcpjyoaUnJEWcHbYVsT67NWQkU3obfruTasIxTe1tdUSuv+pw6dcpcvXo1bGR79I5sPaA5npJaOMfp9m5eUnLE2d7boIgTa3FWgoW3cbYsuTY851TeVlfUhg/lsBGQbRg/27NTCWc7v6HtSkqOQ1mEPh9nQxM+6L90Z2WVeBtnL8koeBuHdWxvKWrjxNVpFGRzwjWocWzhBk3W4WSSowMsD01x1gNEyy5KdVaWj7eWm8BTM7z1BNKim1jeVl/UXrx4UdXn1zZ7A9kaEnF+xxIuzmrKTo44G2sX6R6nNGeFdslFLd7q9inW7EJ7W3VR27wBRT7kXeONwjZ+VEILF2tFpSZHnI21g/IZpxRnhTjeptl35Nr43EN5W3VRK28WW1tbM7u7u/EjajkislmC8twslHCep9naXanJEWdbQ179E7k7KwHE23TbmFybhr1vb6suatOE0H1UZHNn5usM38L5mldXP6Umx651a3keZ9NFIldnhRjepts3MjLepuPvy1uK2nQxdBoZ2ZxweW/sSzjvE2vpkOTYAibiYZyNCHvBULk5K0vA2wWBjHwIbyMDnxtuqLcUtVNA9/b2ph7pu4ts6WMyVLhYK6glOeJsrB2V7zi5OCuE8VbHPiPXpo9DX28pat+JnbxZbGVlxTzwwAOHvphBPvz9N7/5TbDj8pW90v/8V/cuOj4t25NPPjmz8xa1lwa5HJfrJYWD8J6+aTx+/vx588UvfnG0Z2TfyM/nPvc5s7+/Pz31ZPdrSI44O9leqRzX6GbbvyHanZVo4i25VvZBaJ9L9pai9p28IG8Wu+GGG0bFycbGxiRbGGPk1SApWtqOf+ITnzB//OMfx+d0tZ/vp0nO85/C0Hb8U5/61LiYunTp0njctva5HBcuwnn+1TfNx+f/N/mnP/1pHI+Ud2pIjjg72WGpHNfs5oSOGf3b3fzbotVZmS/ekmtlH4T2uWRvKWqn/uWT/x1JsLe3t6eOmtErtG3Hb775ZnPjjTeay5cvj8+R/wW1tV90/MKFC6P28nv6tuy4fGqD/CMtP01hu6y9jOvSf4r2wl3GFX7TN+3HH3744XEs5L6GWw3JUTjj7MFuS+W+djcbF+fnqdFZmSvetudOcq0Z5XAfuXnehzZPtB238bbqolYS4vyfupsgdv3+73//awTwmTNnzGuvvdbVPMjz05ciNIVtkIHodCGBv/zlL+auu+4aFbTvfve7zUsvvbSwXYqDpSZHnE2xm8oZU7OzQhlvD+81cu1hJrUdcfG22qJW/sS9urpqNjc3nffHK6+8Yu6++27zxBNPOJ/r+wQKW99E7fp79tlnzcc//vFRQfvpT3/a/Pvf/7Y7MVKrEpMjzkbaPIUOo91ZwY63s5uPXDvLo8ZHrt5WW9Q+88wz5l3vepc5fvy4+clPfmJeeOEFq59vfOMb5sSJEzOXG6TeaBS2cSPwne98Z3y5wbe//e24g1uOVmJyxFnL4NPsEIEcnJVJ4+0kD5NrD23j6g708bbaovaRRx4xX/va14z8dvmRc1JdbrBsR1PYLqPj57lXX33V3HPPPaOC9siRI+bFF1/003GAXkpMjjgbYKMU3mVOzkoo8HaSj8m1hcu5ZHlDvK2mqJV3Sp87d24JxvyforANF8PnnnvO3HLLLaOC9uTJk+att94KN5iHnktIjjjrYSNU3EVuzkqo8DaPDUuuDRenod5WUdTKm0uaTwqYf2d9uNCk6RnZ/HP/7ne/O94/3/zmN/0PEKDH3JMjzgbYFBV1maOzEh68zWeTkmv9x8qHt1UUtYJePvet9Fdqmy2GbA2JYb//+te/mtOnT48vN5BXDnO55Z4chTPO5rLb9MwzZ2eFIt7q2Us2MyHX2lDqbuPT22KL2r4f1dWNP48WyDYsTlLANpcb3H777ebNN98c1mHks3NMjjj74PgvAnxEn7swuTsrK8Zb97inPoNcOywCvr0tsqjd2dkZfVwXSZIk2Ue373//++Pi4utf/3qfLpKfk1tyxNmDLUOC7KdOCc7KyvG2X/xTn4W3/SIQwtsii1r5xg25hjanPxf32xLdZyFbN6Omxd/+9jdz7733ji83+PnPf948ld3v3JIjzk62GM5OWHTdK8lZWSvedkVc7/N4ax+bkN4WWdTKK7SlvyHMfvsYg2zdtJ5//nkjX8Mo/xm67bbbzOuvv959kuIWuSVHnJ3dTDg7y2PRo9KclTXi7aJI53MMb7tjFdrbIopa+bpabssJIFs7n0cffXR8uYH8GbyEm/bkiLPduwxn2xmV6KysFm/bY57LM3jbHqkY3mZf1J46dWpUkGxvb7eT5JkRAWSb3Qh///vfzX333Te+3OCnP/3pbIOMH2lOjjhrv7FwdpZVyc7KSvF2Nt65PsLb2cjF9Db7olYuM1hbW+Nyg9k91PoI2Q7QXL582XzsYx8bX24gn4ta0k1zcsRZt52Gs3U4K6vEWzc3NLfG2zTeZl/Uat7UWudWu2yPP/74+HKDBx54QGuYBs1Lc3IctLBKT8bZ8p2VrY23ZQmOt/G9zaqolVfT1tfX+VQDD97XKNs//vGPmU83+PGPf+yBpM4utCRHnPW3P3D2iCnZWdkpeOvPFy094W1cb7MqauUbweTd6bfeequW/Zr1PGqS7cUXXzQf+chHxpcbvPbaa1nHrmvyWpIjznZFyu15nHXjlVtrvM0tYnbzxVs7Tj5aZVXUyoIlSdb+pQo+At/0UYNsTzzxxPhyg/vvv79ZetG/tSRHgYyzfrcazvrlqak3vNUUDb9zwVu/PNt6C1LUPvvss+btt99uG9P6uPzpsrQ38FgvPmLDUmWTvXPPPfeMCtojR46YixcvRqSadijX5IizaePlOjrOuhLLoz3e5hGnvrPE277k7M/zXtTKq2JyecAPfvAD+1ksaCnvkF5dXR1dQ7vgaQ55JlCabL/85S/Nhz/84fHlBq+++qpnYrq7c0mOOKs7lm2zw9k2Mvkex9t8Y2c7c7y1JdWvnbeiVr727MyZM0Y+VP2xxx4zP/vZz/rN6J2z5BIDKY7lMy253GAQSuuTS5FN/kMl117LTy2XG8wH2SY54uw8tfwe42x+MVs2Y7xdRqec5/A2XCy9FLXymZ8nTpwYF7Lyys/QolaWzKUH4QLf1nPOsv3zn/80d9111/hygx/96Edtyyz+eFdyxNlytgDOlhNLvC0nll0rwdsuQv2eH1zUSgF79913m1deeWU8gz5F7e7urinlK0rHIDK9k6Nsv/rVr0ZfwiGvzt52223mz3/+c6b0/Ux7WXLEWT+MNfWCs5qi0X8ueNufXY5n4q3/qPUuaqf/dPm///1vZmauRa1cXnD06NHRK2x7e3szffEgDYGcZJP9VvvlBvO7ZFFyxNl5SmU9xtn844m3+cfQdQV460psefteRe0LL7xgjh8/3nqJgWtRK1O8cOHC6KN/lk+XZ2MS0C7b/v6++cIXvjC+3OCHP/xhTDyqx5pPjjirOlzeJoez3lAm6Qhvk2BPPije+guBc1ErBat8TNL05Qbz07Eparledp6azsdaZXv55ZfNBz/4wVFBK5cbyKdlcJsQmE6OODvhUsM9nM03ynibb+yGzhxvhxI8ON+pqP3kJz9pHnnkETN/ucH8VLqKWrl2Vj6ui0JknpzOx9pke/TRR7ncoGOrNMkRZztAFfo0zuYZWLzNM26+Zo23w0k6FbUf+tCHzJ133tn589GPfnT0+bLSdmNjw/z2t7+dmen29vaoKJE3h3HLg4AG2V5//XWzubk5vtzg6aefzgNeglk2yRFnE8BXMiTOKgmEwzTw1gFWoU3xdlhgnYraJ5980rz11ludPw899JB55plnRu1E0vmiVqbMq7TDApfi7JSy/frXvzYf+MAHxpcbXLlyJQWCbMZskiPOZhOyIBPF2SBYg3WKt8HQZtUx3vYPl1NRe/78eauRpi8/kEsNvvKVr/AFClbk9DdKIdv3vvc9Ljdw3BpNcsRZR3AFNsfZfIKKt/nEKvRM8bYf4eBF7c033zwqSOTPxtzKIBBLtjfeeMN8/vOf53KDHttmSHLE2R7AlZ+Cs8oD9M708DaPOMWaJd66kw5e1MqrtDfddBOXG7jHRvUZoWV76aWXzPvf//7x5Qa///3vVfPQNrkhyRFntUXTz3xw1g/HkL3gbUi6efaNt25xC17UyuUHi66pdZsmrTUSCCWbfMIGX6YwLOJDkiPODmOv+Wyc1RwdY/BWd3xSzQ5v7cl7LWrls2fX19dHYsrXlsqNBGkfjBxb+pTtzTffNJ/97Ge53MDDRrBNjjjrAXZmXeCs3oDhrd7YpJ4Z3tpFwGtRKx/RJa+wra2tjUenqB2jKPaOD9l+8YtfmPe9733jyw1+97vfFcsrxsJskyPOxoiGvjFwVl9MZEZ4qzMuWmaFt92R8FrUynDydbfXr18fj0xRO0ZR9J0hsslHwE1fbtD15R5Fg/S0ONvkKMPhrCfomXWDs/oChrf6YqJtRni7PCKDilr502XX581S1C4PQEnPusr2r3/9a/RFHlLQHjlyxPBlCv52Q1tyxFl/jEvoCWd1RRFvdcVD62zwtj0yvYtaKWblq27lZ/qV2fmhKGrniZT92Fa2y5cvm/e+971cbhBoOyxKjjgbCHbm3eKsngDirZ5YaJ8J3i6OUO+iVrqTr8A9deoURe1ittUe7ZLtW9/61szlBm+//Xa1rEItfFFylLFwNhTxvPvFWR3xw1sdcchlFnh7OFKDitplr9A2Q/FKbUOirt+LZJMvU/jMZz4zKmi53CDsfmhLjjgblnvOveNs+ujhbfoY5DYDvJ2NmFNRKx/X5XqjqHUlVk77adm2tx7d+xEAAAHTSURBVLfNe97zHi43iBTeJjnibCTghQyDs2kDibdp+ec6Ot5OIudU1DbvUOf3yvjP57BwY3H//feb//znP5MdyL0gBJrkyP5025/wOswLZ4MourBTvD28/3CyH5NavbUqasW+ra0tCrmVfpsLKQ+48ekGC/NYsIM4i69D/+3B2WB6tnaMt3iLt616dD5hXdR29kQDCEAAAhCAAAQgAAEIJCJAUZsIPMNCAAIQgAAEIAABCPgjQFHrjyU9QQACEIAABCAAAQgkIkBRmwg8w0IAAhCAAAQgAAEI+CNAUeuPJT1BAAIQgAAEIAABCCQiQFGbCDzDQgACEIAABCAAAQj4I0BR648lPUEAAhCAAAQgAAEIJCJAUZsIPMNCAAIQgAAEIAABCPgjQFHrjyU9QQACEIAABCAAAQgkIkBRmwg8w0IAAhCAAAQgAAEI+CNAUeuPJT1BAAIQgAAEIAABCCQiQFGbCDzDQgACEIAABCAAAQj4I0BR648lPUEAAhCAAAQgAAEIJCJAUZsIPMNCAAIQgAAEIAABCPgjQFHrjyU9QQACEIAABCAAAQgkIkBRmwg8w0IAAhCAAAQgAAEI+CNAUeuPJT1BAAIQgAAEIAABCCQi8H/3pg7M8WgUzwAAAABJRU5ErkJggg==[/img][br]
[size=150]A monster truck wheel has an area of [math]324\pi[/math] square inches. A toy company wants to create a scaled copy of the monster truck with a wheel area of [math]9\pi[/math] square inches. What scale factor should the company use?[/size]