Parametervariation Klasse 10
Entlang dieses Geogebra-Buchs sollen die Auswirkungen von Parametern in Funktionsgleichungen untersucht und verglichen werden.
目次
- Lektion 1
- Parametervariation bei der Parabel 1
- Parametervariation bei der Exponentialfunktion 1
- Lektion 2
- Parametervariation bei Parabeln 2
- Parametervariation bei Exponentialfunktionen 2
- Lektion 3
- Parametervariation bei der Parabel 3
- Parametervariation bei der Exponentialfunktion 3
Parametervariation bei der Parabel 1
Einführung
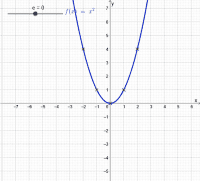
Gegeben ist der Graph der Funktion f mit f(x)=x². [br]Zur Funktionsgleichung wird nun auf beiden Seiten ein konstanter Wert ( hier "e" genannt) addiert. [br]Es entsteht der Graph der neuen Funktion g mit g(x)=f(x)+e. [br]Bewege den Schieberegler, um Dir darüber einen Eindruck zu verschaffen.
Fülle die Lücken im folgenden Text:
_[size=100]________________ man in der Funktionsgleichung von [math]f[/math] mit [math]f(x)=x^2[/math] einen konstanten Wert[br] [br](umgangssprachlich: "eine Zahl"), so verändern sich die [br][br]______________________ (___-Werte) aller Punkte auf dem Graphen der Funktion f um [br][br]_______________________________________________.[br][br]Dadurch wird der Graph der Ausgangsfunktion f um ___________________________ in ____-Richtung[br][br] ____________________. [br][br]Man erhält den Graph der neuen Funktion g mit g(x)= _________.[br][/size]
Aufgabe 1
[b]Beschreibe[/b], wie sich der Graph der Funktion [math]f[/math]mit [math]f(x)=x^2[/math] verändert hat.[br]a.) [math]g(x)=f(x)+\frac{2}{3}[/math][br]b.) [math]g(x)=f(x)+(-3,8)[/math][br]c.) [math]g(x)=f(x)-\frac{5}{4}[/math][br]d.)[b] Erkläre[/b] in eigenen Worten, wie die Auswirkungen bei c.) zustande kommen ([i]Erwartung: [u]Mindestens[/u] 2-3 vollständige Sätze[/i]). [br]
Aufgabe 2
Die Punkte A(1|1), B(1,5|2,25), C(2|f(2)) und D(2,5|f(2,5)) liegen auf dem Graphen der Funktion [math]f[/math] mit [math]f(x)=x^2[/math].[br]Es nun gilt: [math]g(x)=f(x)+4,2[/math][br]a.) Was ändert sich an den Koordinaten der gegebenen Punkte?[br]b.) Berechne die Koordinaten der neuen Punkte A', B' , C' und D'.
Parametervariation bei Parabeln 2
Einführung
Der Parameter wird nun nicht [u]nach Berechnung[/u] des ursprünglichen Funktionswerts addiert, sondern direkt innerhalb der Funktionsgleichung zur Variablen "x" addiert bzw. subtrahiert, [u][b]bevor man den Funktionswert berechnet.[br][/b][/u][br]
Verändere den Wert des Parameters d mit dem Schieberegler.
Aufgabe 1
Vervollständige die beiden Sätze und gib für jeden Satz auch eine Funktionsgleichung zwei Funktionsgleichungen als Beispiele an.[br]1.) Ist der Wert von d positiv, dann....[br]2.) Ist der Wert von d negativ, dann...
Aufgabe 2
Gegeben ist die Funktion f mit f(x)=x².[br]In der Regel wird der Funktionsterm der verschobenen Parabel in der Form g(x)=(x [b]-[/b] d)² angegeben.[br][br]a.) Susi sagt: " Man muss hier ja höllisch auf das Vorzeichen des Parameters d achten!" [br]Nimm zu dieser Aussage Stellung. [br][br]b.) Wird das ganze nicht viel einfacher, wenn man g(x)=(x [b]+[/b] d)² verwendet? [br]Erläutere an Beispielen und 2-3 Sätzen, weshalb dieses nicht sinnvoll ist.[br]
Verständnisbooster????
[b]Nicht Auswendiglernen, sondern Verstehen![/b]☝🏻[br]Warum verschiebt sich der Graph für positive Werte von d nach rechts, wenn doch der Funktionsterm dann (x [b]- [/b]d)² lautet? [br]Als Beispiel nutzen wir f(x)=x² und g(x)=(x-1)².[br][br]Setze zur Untersuchung Zahlen für x ein und vergleiche die Funktionswerte f(x) und g(x). [br]Wähle dazu z.B. x=2 und x = 3![br][br][br]
Parametervariation bei der Parabel 3
Einführung
In dieser Lektion wird die gesamte Funktion f mit dem Parameter [b]multipliziert [/b]und die Auswirkungen dessen untersucht.
Verändere den Parameter a
Aufgabe 1
Was verändert sich, wenn man eine Funktionsgleichung mit einem konstanten Faktor multipliziert?[br][b]Beschreibe[/b] deine Beobachtungen und [b]klassifiziere[/b] (sortiere in Gruppen/Bereiche) bezüglich Werten des Parameters a.
Aufgabe 2
Betrachte die gegebenen Punkte E und C im Applet.[br]Wie verändern sich die beiden [b]Koordinaten[/b] der Punkte, wenn man den Wert des Parameters variiert?[br]a.) [b]Beschreibe[/b] deine Beobachtungen.[br]b.) [b]Berechne[/b] die neuen Koordinaten der Punkte E' und C',...[br][list][*] wenn a = 2,[/*][*]wenn a = 0,5,[/*][*]wenn a = -3 beträgt.[/*][/list]c.) [b]Erkläre[/b] deinen Rechenweg. Warum funktioniert das so? [br]d.) Es gibt einen Punkt, der unverändert bleibt. Gib diesen Punkt an.