IM Geo.5.8 Lesson: Speaking of Scaling
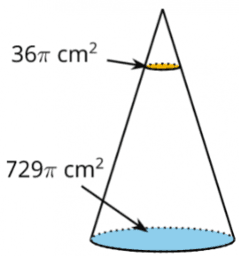
[size=150]The image shows a cone that has a base with area [math]36\pi[/math] square centimeters. The cone has been dilated using the top vertex as a center. The area of the dilated cone’s base is [math]729\pi[/math] square centimeters.[/size][br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAATgAAAFNCAYAAACUkHMYAAAgAElEQVR4Ae19B7gURfY98IgGMqKCAoIBAzmIkkR0RTJmJCkmMiZcyYJKDuuqSNRVV0RA3J+JoCvqSk4uSlRhVTKCSnok7/87zb/aej09MzU93T1d3be+771OVbeqTlWfuVVdfToXcWAEGAFGIKQI5AppvbhajAAjwAgQExx3AkaAEQgtAkxwoW1arhgjwAgwwXEfYAQYgdAiwAQX2qblijECjAATHPcBRoARCC0CTHChbVquGCPACDDBcR9gBBiB0CLABBfapuWKMQKMABMc9wFGgBEILQJMcKFtWq6YXwj07duXHn74YerQoQPt37/fr2w5HwUEmOAUQOIojEAiBEqXLk25cuUy/l577bVEUfmazwgwwfkMOGcXLgRWrlxpkhtI7vbbbw9XBTWvDROc5g3Ixc8sAkOGDMlBcAUKFKCTJ09mtlCcu4kAE5wJBe8wAqkjULNmTYPgihcvbhLdvHnzUjfEKTxBgAnOE1jZaBQQ2LJli0lqnTt3Nve7du0aheprUUcmOC2aiQsZRATGjx9vktrHH39M119/vXGMhw4cgoEAE1ww2oFLoSECTZo0MQitaNGiRulHjhxpEt6///1vDWsUviIzwYWvTblGPiCwd+9ek8yw/g3hm2++Mc899thjPpSCs0iGABNcMoT4OiNgg8CMGTNMMnv77bfNGFdffbVx/rLLLjPP8U7mEGCCyxz2nLPGCLRt29YkuMOHD5s1efrpp83zq1evNs/zTmYQYILLDO6cq8YIHD9+nPLly2cQWcuWLXPU5KuvvjIJ7plnnslxjQ/8R4AJzn/MOUfNEZg7d65JYpMnT46pzUUXXWRcr127dsw1PuEvAkxw/uLNuYUAgfvuu88kuB07dsTUqFu3bub17777LuY6n/APASY4/7DmnEKCQKlSpQwCa9iwoW2NPvroI5PgJk6caBuHT/qDABOcPzhzLiFB4JNPPjHJa/To0XFrVbhwYSNe06ZN48bhC94jwATnPcacQ4gQgPabkEbasGFD3Jq1b9/ejLdv37648fiCtwgwwXmLL1sPGQKVKlUyiKtKlSoJa/bWW2+ZBPfqq68mjMsXvUOACc47bNlyyBCQtd8GDBiQsHaHDh0yCe62225LGJcveocAE5x32LLlkCEga78tXbo0ae2aN29ukBxrxCWFyrMITHCeQcuGw4aA0H4rV66cUtUmTZpkenHvvvuuUhqO5C4CTHDu4snWQoqArP3Wo0cPpVr+/PPPJsHdf//9Smk4krsIMMG5iydbCykCsvbb/PnzlWtZv359g+TOO+885TQc0T0EmODcw5IthRgBq/abalVZI04VKW/iMcF5gytbDRECe/bsMYeaQvtNtXqsEaeKlDfxmOC8wZWthgiB6dOnmwQna7+pVvGaa64x0l966aWqSTieSwgwwbkEJJsJLwJC+y137tx05MiRlCvKGnEpQ+ZaAiY416BkQ2FEIDs7O672m2p9WSNOFSn34zHBuY8pWwwRAnPmzDGHp3bab6pVZY04VaTcjccE5y6ebC1kCHTp0sUkuJ07dzquXffu3U07rBHnGMaUEzLBpQwZJ4gSAiVLljSIKZ72myoWrBGnipS78Zjg3MWTrYUIAVXtN9Uqs0acKlLuxWOCcw9LthQyBPr06WMOKxNpv6lWmzXiVJFyLx4TnHtYsqWQIVCxYkWD4KpWrepKzWbOnGkSJmvEuQJpUiNMcEkh4ghRRCAV7TdVfFgjThUp9+IxwbmHJVsKEQKpar+pVl3WiDtx4oRqMo7nEAEmOIfAcbJwI5Cq9psqGq+88oo5TGWNOFXUnMdjgnOOHacMKQKy9lvPnj1drSVrxLkKZ1JjTHBJIeIIUUPAqfabKk6sEaeKVPrxmODSx5AthAwBp9pvqjDIGnGffvqpajKO5wABJjgHoHGS8CIga7917NjRk4p+++235jzco48+6kkebPQMAkxw3BMYAQkBWftt1qxZ0hV3d1kjzl0841ljgouHDJ+PJALpar+pgiZrxK1atUo1GcdLEQEmuBQB0yn62rVrafHixYQth+QIuKH9ljyXMzFkjbihQ4eqJuN4KSLABJciYDpExyLVokWLmvM8uXLlovLly9O8efN0KH7Gyihrv02ZMsXzclx88cVGG9WqVcvzvKKaARNcyFp+woQJxk0Dkvvss8+M2oHY8D4liI69ufgN7pb2W/wccl5hjbiceHhxxATnBaoZtrlt27aYEuAcCA7Ex8EeAbe03+ytx55ljbhYTNw+wwTnNqIBtgeCa9SoUYBLmLmiLVq0yPgBAEajR4/2rSBCI+7GG2/0Lc8oZeQawUH+pU2bNjFzP5gLguufytDo4MGDNHHiRMMeOpz8B3scUkcAmAJH9uDssZO13zZu3GgfyYOz9957r9m/9+3b50EO0TaZNsFhfsc6oS0TkryvooEFe5gQl9NhH56HOBftJnNWezE3l8oPjbOc9EzltvabKgqsEaeKlLN4aROcIJ5y5coRbiLr/A9IDdcEOSW6wRBXxEMaHMPzkIP1WL7G+/YIoE3wI9S6dWv7CBE/u2LFCrPfDRgwwFc0WCPOW7jTJjgQDogtUQCpFSlSxOhEnTt3to0qbkIQHOIwkdnClPJJ4FitWjXjKSpjag/f4MGDTYJbunSpfSQPz7Zo0cLIv0CBAsQace4CnTbBqRZHeHrxJrlBaiA3eG58I6qimjieIDf8uFg968Qpo3W1Ro0aRt/D1EgmAmvEeYe6bwSH4REIzI7gcCOKoanKPJ13cKRmGevM+vbtS40bNza8JGzxh3PWoTjiYsW6WJsGwhFpRTo8jLESEezgvJyHykMbmdysZUmtluGOvXnzZrPvua39pooca8SpIpV6PN8ITszD2Q1RxdwbPA1dgvA4BTFbt9Z64ukl4mCL+iZ6MCNIXqSx2hbHIp4VM0FuWNxrJUxr3Kgfjxs3ziS4+fPnZwwO1ojzBnpfCE48wcONKTwYuTqCLOy8Ozmeyj5ubrx/qfrnxLsRw23UB/sgGtQLfyAleKvW16IEWWEYBHID+cjpsC/mKXEd3h7sJ4qH61YCk8kN+xwSI3DDDTcYOBcrVixxRI+vjho1yiRa1ohzD2xPCQ43H4ZTuBHxh5vcLgjCENdBFEiHyXGkAylgjZ0dOcr25LVMIk+VrWwj2T6ISNjEvmoQBIe0IC078kH9hG1s4xG+HM/6gEdMBQA/kKTdn5UUVesQtnh+aL+pYsYacapIpRbPVYLDDSnmk+Qb1c6jkYsp4oIEhDcnzlm3uHHtAtLBAwLJwQ7+MCwW+9iifIgnn0tGmta8xFA7HvlY44tj5CnqYvXuRBxsQX4iXiLvUsQDtnJA/VG2RH+J7Mq2wr7vl/abKo6sEaeKlHo8VwlO3JjyFt4XSOm1116LWyoRH3GxDxKSvQzsy94ZyEIOIAyrVwQPyUpC1mPZhso+yiHKmor3BtsywSXKS3hgyeYjUReUJd06JSpL2K/5pf2miiNrxKkipR7PVYKDNyT+hJckPB7cjBhy2g3NBGlgm4g4hHeHOSphRxCZOBZVB+lZiRAkmE6Qh4apekGC4JKVQcRLRlxMcOm0JJGs/daqVav0jLmUesmSJeYPKKYWOKSPgKsEF684IAYxgY4hrDUIggOBJQqyByUP82RvT6SHLeQrAggpGWmIuPG2gnxQ3lSDSJusDKrxmOBSbYGc8f3WfsuZe/wj1oiLj42TK6nfqU5yITLedhBEZvV+xPlE3pvIVhAliCBegDdnJSFMxicj0Hj2xHlBPlbb4nqirUjLBJcIJf+uYdpE9LudO3f6l3GSnGSNuK1btyaJzZeTIeAbwcnel5XIBGlZnwjaFV54LokIDvatk++InyiNXV7Wc7ArbgrrtWTHTHDJEPL3ut/ab6q1+/jjj80+pnI/qNqNajzfCA4AC3KwEo0gLTxISBbEnJ7VhpwO81zWzoE80vXg5Dk4efgr5x1vnwkuHjL+n5e138aMGeN/AZLkKH7wWSMuCVAKl30jOJkc5PkzlBFkBPLDU9REQfYCrTZEOgx/Ycs6DAbB4S/dIEhahYzlvJjgZDSc7aP9rQ+TnFiSn8j7qf2mWlbWiFNFKnk83whOeGkgCGsnxbH41UrkmQmSQFyrDVFVeGm4bg3IPxmBWtPYHcM+6iA/ybWLZz0nyp6MZFXjCTyT2bOWw+kxnjpi+PTDDz84NZF2OrQ5vHM8YYzX/iqZZEr7TaVsiCNrxM2YMUM1GcezQSAtgoNXhqeiWOMWr8PhVxdvIQjPJx6BCS8O8aDmaw3y9Xg2hIdnnX+DLUEIiJNOgGcoyBjLXqyeImzjnHWeUZW4VOOJ+vhFcF9//bXZhgULFjSI5s4776RBgwbRG2+8QdBU++2339KBViktsBU/ME6ITtZ+GzhwoFKefkeSNeLatWvnd/ahyi9tghPEhS08JPEmA7Zi4a6Ik2wOTHhHVlvwllRsCHKwkgtaTBCC3bVUW1R+2GAtqyinlXhE2aznrXmrxhP1SWbPat/p8ezZs802EHW025YtW5aaNGlC3bp1M36o4PV9//33TrO1TSf/2KFvJFpEbjUga78tW7bMejkwx0IjLn/+/KwRl0arpEVw8NpwQ2LYYNfZxTl4VPHmzKxlB3mIBwkiPbbwmpBXooB08Yav4qbA1o0AT0KQjFxOUVZrPqrEpRpP5O0Xwa1bt45mzZpFw4YNow4dOlDt2rVJfDDFWn+7Y9nrg+eUrtcn6i/ywo+pCtFlWvtNte+xRpwqUonjpUVwsmmQHYas1j85Tir7IBBhC/sqAfESDUFhz+1gV2+38wiyvZ9++omgfvHyyy8br9PdcsstdMkllyT8wROkJLZlypQxvT78MOBzesm8PuAupgqEHWwTEV0QtN9U21LWiLvvvvtUk3E8CwKuEZzFLh9GHIFjx46R8PqGDx/u2OurUqUK3XHHHSS8vuXLl9Ovv/5qoIsfLJnc5H07opO13xYsWBDTQiBNu4CnrphyiffkXOQbz5vGMBrp402PQNrLLjRo0MCoX6lSpewu8zkFBJjgFEDiKO4iAO9EeH1QNW7WrJljr08ocAiSsW7xIEh47vG038T0BdKK8Ef2Xjr9+7d0av/n1LDeVQbRNKxbiY5vfZayNz5F2d/0omNrO9CxNXeZJNugRgk6tvp2OramPWWv60LZ3z5Gxzf/+b2HQY/dTif3LqBTB1fS6SPb6I9Th42yiTKLcooysEacQML59s8WdW6DUzICriAArw9Pa9955x0SXl+dOnVsh6KCFFS31113nUlEHTt2NMt76uAqGtjnVvPazg8upiMLcuX4698hi+pfk5d6tMmb47yIh+v4m/x4znTiOtLib+nLsdfnjy1g5n1800A6uftf9Ef2LqN8rBFnNpPjHSY4x9BxQj8REF7fpEmTjG9ZOPH6BBmOHfYAZW943CQrEE+LevkMktrweiwJCaLyYov8Rj2cFUOex1bcSid+nE4FCuQ3CJCHqc56GxOcM9w4VYYRwHyZvL5SkJfqtkGVvPTxGH/JLFWCBPHK9bEOYTPcBFpkzwSnRTNxIWUEcKNb11jKRJBov2D+3HRD9bw0tEueQBPc7nm5qNX1eemcQnmo8Nl5DKJ77LHHZBh4XwEBJjgFkDhKcBAQ6wQTkRiu4YkmFo7jAQLeeIgX/7KLsuiKi/PSTbXy0dzhuWj+WH+9OgxRx3TLQ1Mez0MDOmRRy+vyUbnSWbblrVWrVnAaQpOSMMFp0lBRLyaGpFhqYSUqLDLHQnIQHzw7u3WQ8hsyeL3Mbv2c1S6Oq1TMojIl89AlF54hHhCQ9e/xu7IMgvrH02fIEQQp4vRsm5cwFMYf9nFeHBc554xXZpevfA5vMlSuXNmsN2vEpXYnMMGlhhfHzgACIC4QGbwyEBneilFd/I3ilihRwiAIeZ0a1qRhXZsq2cmk4+U+3sYRhC3ImjXinHc6Jjjn2HFKDRBQ1X7DUBZEii1IFF4fCDEry3646JTkQKiwiz8QLLb3338/vf/++7bep4BYEDFrxAlE1LZMcGo4cSxNEQCJCDJyS/sNw2WQIUgJhIg/SBzhnPwnXjeM94ZEKpDKGnF79+5NJWmk4zLBRbr5w195of2GNxp0Dm+//bZJ1KwRp96STHDqWHFMzRDQQftNFdLDhw+bBMcacaqoETHBqWPFMTVDQBftN1VYZY2448ePqyaLdDwmuEg3f7grr4v2m2oryBpxc+fOVU0W6XhMcJFu/vBWXtZ+69WrVygqumPHDnOYyhpxak3KBKeGE8fSDIFk2m+aVccsLmvEmVAo7TDBKcHEkXRDIJ72m271sJZX1oj75JNPrJf52IIAE5wFED7UH4Hdu3ebQzlZ+03/mhHJGnEQC+WQGAEmuMT48FUNEZg2bZpJcBDPDFuAjDsWL1eqVClsVXO9PkxwrkPKBjONgNCJy5MnDx09ejTTxXE9//79+5sEvmrVKtfth8kgE1yYWpPrQpA9z5s3r0EArVq1CiUiS5YsMQkO781yiI8AE1x8bPiKhgjIH6ieOnWqhjVQK7L4dnDNmjXVEkQ0FhNcRBs+rNWWtd927Trz8ZYw1rVHjx6mF8cacfFbmAkuPjZ8RUME7LTfNKxG0iKzRlxSiIwITHBqOHEsDRBYuHCh6dWMGTNGgxKnV0TWiEuOHxNccow4hiYI9O7d2yQ4t7Tfglz1Dh06mPVljTj7lmKCs8eFz2qIwCWXXGLc8Lprv6lCzxpxyZFigkuOEcfQAIHly5eb3szAgQM1KHH6RWSNuOQYMsElx4hjaIDAoEGDTIJbtmyZBiV2p4isEZcYRya4xPjwVU0QqF69ukFwFSpU0KTE7hRz8uTJJrGzRlwspkxwsZjwGc0QCKP2m2oTsEZcYqSY4BLjw1c1QCCs2m+q0LNGXHykmODiY8NXNEEgrNpvqvCPHj3aHKayRlxO1JjgcuLBR5ohIGu/derUSbPSu1PcDRs2mATHGnE5MWWCy4kHH2mGQNi131SbgzXi7JFigrPHhc9qgkDYtd9Um0HWiFu5cqVqstDHY4ILfROHt4Ky9lvr1q3DW1GFmi1dutQcprJG3J+AMcH9iQXvaYZAVLTfVJuFNeJikWKCi8WEz2iCQFS031SbgzXiYpFigovFhM9ogkBUtN9Um0PWiBs/frxqslDHY4ILdfOGt3Ky9tvYsWPDW9EUa1a0aFFjLq5JkyYppgxndCa4cLZr6Gsla79t2rQp9PVVrSBrxOVEigkuJx58pAkCUdN+U20WWSNu+vTpqslCG48JLrRNG96KRVH7TbU1ZY24tm3bqiYLbTwmuNA2bXgrJmu/gew45ESgZcuWxjxcvnz56Pjx4zkvRuyICS5iDR6G6kZV+0217Vgj7k+kmOD+xIL3NEAADxRy5cpl/PXq1UuDEvtfRNaI+xNzJrg/seA9DRDAkhBBcAsWLNCgxJkpYsOGDQ2cSpUqlZkCBCRXJriANAQXQw2Bxo0bGzdu8eLF1RJENBZrxJ1peCa4iN4AOlZ7165dpvcWVe031XZjjTgmONW+wvECgsDUqVNNgnvnnXcCUqrgFoM14ojYgwtu/+SSWRCAJBLm37Kysujo0aOWq3xoRWDAgAHmD0JUNeKY4Ky9go8DiQC030BsILioa7+pNhBrxLEHp9pXOF6GEWDtN2cNEHWNOPbgnPUbTuUzAqz95gxwWSNuy5YtzoxonIoJTuPGi1LRsSwEw1MsE+GgjsD8+fPNebgoasQxwan3FY6ZIQRY+y094KOsEccEl17f4dQ+IMDab+mBLGvE7dmzJz1jmqVmgtOswaJYXNZ+S6/Vo6wRxwSXXt/h1B4jIGu/QSaJQ+oIHDlyhHLnzm3MxUVNI44JLvX+wil8RIC139wBO6oacUxw7vQftuIRAqz95g6wskbcnDlz3DGqgRUmOA0aKapFlLXf8KCBg3MEZI24Ll26ODekWUomOM0aLErFlbXfsFSEQ3oICI24kiVLpmdIo9RMcBo1VtSKytpv7rZ4FDXimODc7UNszSUEWPvNJSAlM7JGXJ8+faQr4d1lggtv22pdM1n7DS/ac3AHgapVqxrLRSpWrOiOwYBbYYILeANFtXiy9hukkji4g0DUNOKY4NzpN2zFRQQgZsnaby4CKpmKmkYcE5zU+LwbDAQgRy6+nIWhKgd3EYiSRhwTnLt9h625gAA+KCMIDg8bOLiLQM+ePU18w64RxwTnbt9hay4gwNpvLoCYwESUNOKY4BJ0BL7kPwL4mLPw3rDQl4M3CERFI44Jzpv+w1YdItCrVy+T4PCqFgdvEOjYsaOJc5g14pjgvOk/bNUhAhUqVDBuPLxkz8E7BGbNmmUS3PTp073LKMOWmeAy3ACc/Z8ILFu2zLzpWPvtT1y82IuKRhwTnBe9h206QmDgwIEmwUHokoO3CMgacdnZ2d5mliHrTHAZAp6zjUWgWrVqBsFBopyD9whMmTLF/EEJq0YcE5z3/YhzUECAtd8UQHI5ys6dO02CC6tGHBOcy52GzTlDgLXfnOGWbqqwa8QxwaXbQzi9Kwiw9psrMKZsRNaIW7RoUcrpg56ACS7oLRSB8snab507d45AjYNTxbBrxDHBBaevRbYkrP2W2aYPs0YcE1xm+xbnTkSs/ZbZbhBmjTgmuMz2rcjnztpvme8Cskbc4MGDM18gF0vABOcimGwqdQRk7bdp06alboBTuIJA+fLljSUjNWrUcMVeUIwwwQWlJSJaDln7bffu3RFFIfPVDqtGHBNc5vtWpEvA2m/BaH5ZI27cuHHBKJQLpWCCcwFENuEMAdZ+c4abV6mKFStmDFNvuOEGr7Lw3S4TnO+Qc4YCAVn7bfPmzeI0bzOEQBg14pjgMtSZOFsi1n4LVi8Io0YcE1yw+lhkSsPab8Fralkjrk2bNsEroIMSMcE5AI2TpI8Aa7+lj6EXFlq1amXMw+XNm5fCoBHHBOdFL2GbSRFg7bekEGUkQtg04pjgMtKNop3pxo0bTR2y3r17RxuMgNU+bBpxTHAB62BRKM6YMWNMglu4cGEUqqxVHcOkEccEp1XXC0dhGzVqZBBciRIlwlGhkNVC/gHSXSOOCS5knTPo1ZGHQKz9FszWkqcQ+vTpE8xCKpaKCU4RKI7mDgLyJPbs2bPdMcpWXEcgLBpxTHCudw02mAgBsQwhKyuLjh07ligqX8sgAvIynhUrVmSwJOllzQSXHn6cOgUEoP2WJ08eY/4tLAtJU6i+VlHlhdg6a8QxwWnV7fQuLGu/6dV+YdCIY4LTq89pXVrWftOr+WSNOF3FEJjg9OpzWpdWaL+FSY5H6wZJUvgwaMQxwSVpZL7sDgKy9luYBBXdQSe4VnTXiGOCC27fClXJWPtNz+bUXSOOCU7PfqddqVn7TbsmMwosa8Tp+FEgJjg9+51WpQ7LkgOtQHepsNCI03lpDxOcSx2BzcRHICyLRuPXMNxXxOJsHTXimODC3TcDUTvWfgtEMzguhPx63Zw5cxzbyURCJrhMoB6hPOUXt1n7Tc+G11kggQlOzz6nTall6R3WftOm2WIKqqvEFRNcTFPyCTcR0PXGcBODMNiSf6h00ohjggtD7wtoHXQe2gQU0owVS55q0EkjjgkuY10m/BnLk9Os/aZ/e+v4sIgJTv9+F9gayMsLWPstsM2kXDAdl/swwSk3L0dMBQHdF4imUteoxNVxwTYTXFR6p8/11P0VH5/h0iY73TTimOC06Vp6FVR+SXv37t16FZ5LGxcB3UQTmODiNiVfSAcB3WV20ql7mNPqJnvFBBfm3pihuoVBKDFD0GmRrU4/XkxwWnQpbwq5bds2Wrx4sfGHfbdCGKSu3cIijHZ0mn5gggtjD0xSp3nz5pGYLM6VK5fxlStsu3TpQgcPHkySOvllYbtGjRrJI3MM7RDQ6eNBTHDada/0CgwCK1KkCLVu3ZpAdAg4N2TIEIPo0l2lruNSgvQQjV5qnT7/yAQXvf4Z10sT742mA4mOi0HTqW9U08qLuLOzswMLQ8YIbu3atYS/dMJnn30W92ZNx25U0wovLp366/g6Tzr1jWpaXV7DUyI4eZ5GZR/EYw2YxB46dKjt3A9uCjFcsqazHr/66qskbiJRlqJFi1Lfvn3JzYlya75ROMawFcNXp0HXF7Kd1jfK6XQRUvCF4CZMmGBOZAtSKleuXMw5THLHC5gnaty4cY40VhsgunS9wnj5h/08fhzQNp07d3ZcVV0ldRxXOOIJxZRGiRIlAouEEsHBI0v2J4Y3uElkTwqEI0gNgFg9NcQVQCEePDS7gBtP2AFhygFlq1q1qnEdJOfGk0DZfhT2hfeWDnaiHYPc4aPQln7VUYcfNCWCUwFMdG47DwCkZSU2q01BUBh+WgMILB65ibi4MYVHZ1cGEY+3sQiIHw/g7DTIQ5ZEnrhT+5wueAjIUxJBlaN3heBkAnJ6k8geoLUpsXQBBAcCSxTkcqTjiSTKI2zXBLnF85xV6ytPOuv2YRLVOnK8WATEfPgll1wSezEAZ1whOHGTwItzGhKRk/AOMYxKFoQXl8xjTGbHjesYfuPBCuYOMXQGSWMRbJs2bWjixIk5htIYyiOeWIcGgkYckRbpsI9zckA8OQ/kYxdPTiP2RbulS26wp8uyAVF33rqDQNCXBaVNcGJyGjdvOqQiP4iwQi8IDl5espBK3GS20rkO0hCkJobX1q3sZQqCF3OI4pfRmgbHYhiPNInyQDw5D7k+bpIba7/JyEZrX17YPWjQoMBVPm2CEzdKsuFjspoLO3ZeoCAt4d0ksgUvDyRgZwfpcMOL9y9Vt/FIIl45QG6CmIALjkFG+MOPAOphJWtBcILAsFwDceDZIX9cF3VDHMxzgdwQD/bjxbPmgzILrJHOjcDab26gqK+NChUqGP29evXqgatEWgSHG0/cyOncLLIXaGdH3NjxSEtGVQxR7eKCJBJ5PKIu1q31qa2cn94pkkEAABx3SURBVHUfmIg88OBElRxlgkP+ICy7IMgecUBuyeJhaCsH4SmjjBjK2v2p/JDINnV6+VouN++7g0CQNeLSIjh4B+JGU72R7SAVN208L1DclMgLRBAvyPGsBCcIBN4LvCgcC08K+/gDueK6OBbbePnZnZfLAOJWDcgL9cMfyhAvyPYTEZEcT7aFOgKbRH+J7Mq2xL5O8jmizLx1D4Ega8Q5JjjZU7EbBqnCJ9+I8bwR5AVvBTc/PBKQgRxAJHiTAddFPJngkB7kabUPIpFJCDe/nQcp55VsH/miHHL+ydLgukxwicogx7PiIOcjx0vnx0e2abfP2m92qETvXPHixY1+jxFBkIJjgpOJyekNhBsZZIC/RDc1AAM5CfJCfPFUEVthA2WyIxjhlVmBxxBSDvHiyXGS7YuypEr6MiGpEpcb8ZLVJ9l11n5LhlA0rnfq1Mm8D4MkUe+Y4MRcV6LhVKKmlclNdUgEbwv5yUQHQsEcnbjZBcHJBGNHwBimWsueypxZvLpFjeDEDwxrv8XrEdE4H1SNOEcEJ5OTPMRTbUo5vZVkVG3EiycIJplHiHyty1qQNt0g8pcJVsWmjh7c0qVLzV/twYMHq1ST44QUgaBqxDm6o4X3luo8E9rWS3LDMFYQTCLihUeHeLJnJwgm3f4n8o8CwQ0YMMDEe8WKFelCx+k1R0CsdsibNy8F5UPfKROcIALcyGJYqNouXpIbyoChLsplnVuzlg/lsMYR9bLGTfVYkH+qnqnIPxmubsdLtX5yfGCI8lasWFE+zfsRRWDq1KnmD97s2bMDgULKBCfmuKwEkaw2Mrmpzrklsylfh8cm1p/hYUOiABKylgEeF25W2atLZCPeNRAb7KAsqQS3iUvVXipllONu2LDB7MxWLOV4vB8dBHbt2mX2iVR/4L1CKSWCk28aEJZqkMktlXSq9kFK4tUmkFeiIOpgnX8TBIfr6QRhHySXyjBVTpeoDG7Hc1rX0aNHm5150aJFTs1wupAhIBygoEhmpURwYoydjETkNpPJDa8Xqb4eJdtItA/74kkenq5a17pZ04oGsHpqguBSISWrbXEscALJ4UV4a17wNq0vzbtNXKr2RJlT3TZs2NAguJIlS6aalOOHGAFZI27hwoUZr6kyweGmxA2bqmciCEWkVd1akcENK9a+ideLxJAUNkG6ychN1AEEZA2CEMSL7NbrqRyD0MT8lKgvyiy8THFOtinyxzXsxwtux4uXT6LzrP2WCJ1oX9u0aZPJE0HQiFMmODG3BC/J6pEkalI3CU4Qg7wFkSSbcxPlE16a3TAZdULd8OdGgD3kB+KVy4t95GGdo3CbuFTtOakra785QS06acQPeRA04pQJLgjNAw8NN674S4VoUX7ER9p4Afbh5bkd5HIn8zLdztsLe6z95gWq4bEpa8QtX748oxXTiuAyihRnbiAA7bfcuXMbXmnbtm0ZFUYgBoEgacQxwcU0D59IhICs/TZ9+vREUflahBEIikYcE1yEO6GTqsvab3v27HFigtNEAIGgaMQxwUWgs7lZRdZ+cxPN8NqSNeLGjh2bsYoywWUMev0ylrXfxo8fr18FuMS+IhAEjTgmOF+bXO/MZO23LVu26F0ZLr3nCARBI44JzvNmDk8G4o0R1n4LT5t6WZMgaMQxwXnZwiGyzdpvIWpMn6oCjbisrCxjSZHd20N+FIMJzg+UQ5AHa7+FoBEzUAXxXjaILhMacUxwGWh0J1nisfuJEyecJHUljXi3lrXfXIEzMkYyrRHHBKdBV5s7d67h5l9xxRWUCYUG1n7ToJMEtIiZ1ohjggtox5CLVbdu3Rwv7D/99NPyZc/3WfvNc4hDnQGUdCAygWUjfgcmOL8Rd5jfU089lYPkrr32WvLrOwis/eaw0TiZgQAW+gpFHb9HIExwGnVCLLS9/PLLzc6CTjNq1ChPa7Bjxw4zPwiWcmAEUkUgkxpxTHCptlaG42dnZ9PDDz9skg5I7pZbbiGvFt5OnjzZzGvOnDkZrj1nrysC1atXN/qR3xpxTHCa9pi3336bSpcubZJPwYIFCWTkdmjZsqWRR758+QjkyoERcILAoEGDzL7qp0YcE5yT1gpImt27d9Ndd91ldhx4c3fffTft3bvXlRIePnyYtd9cQZKNgNTEPBzIzq/ABOcX0h7m88orr1CBAgXMDnT++ecTdNvSDfASRadk7bd00eT0mdCIY4ILSb/DRC7m4gQhYfvII4+ktTi4Q4cOpj3WfgtJR8lgNWSNOPRXPwITnB8o+5jHyJEjTVICyWFxMLS5nATx1bImTZo4Sc5pGIEcCGRCI44JLkcThOMAmvhYJyd7c3/9619TqtzHH39spmftt5Sg48gJEPBbI44JLkFj6H4JpCaTHN6IUH2C1aNHDzOtV0tQdMeXy586An5rxDHBpd5GWqXA4mAMU2WiwzA2WRDfc61Zs2ayqHydEVBGQNaIw4v4XgcmOK8RDoD948ePGw8cZJL7y1/+Qps3b7Ytnaz9ho9Xc2AE3ELAb404Jji3Wk4DO1g6giUkguiwtARLTKxB1n5buXKl9TIfMwJpIeCnRhwTXFpNpV9iLPfAYmBBcthisbC8DIS13/RrV51K7KdGHBOcTj3DxbLitS683iWIDq99YWEva7+5CDKbskVA1ojDQwcvAxOcl+gG3Dbm4KyLg+XlJYsWLQp4Dbh4uiLgl0YcE5yuPcTFckNySXhyYlu4cGEXc2BTjEBOBPzSiGOCy4l7ZI+wPg5LQgTBYQuRTQ6MgBcIyBpxeIXLq8AE5xWyGtqVtd8E0WFxMN6M4MAIuI2A0IjDS/heBSY4r5DV0K7QfsubN2+McvCIESM0rBEXOcgI+KERxwQX5B7gY9ms2m/4RGG3bt1yDFlvvvlm8ksFwseqc1YZQsAPjTgmuAw1btCyjaf9hsXBF1xwgUl0+fPnp0mTJgWt+FweTRGAhDmmQ6pVq+ZJDZjgPIFVP6OJtN+gEHzPPfeYJIcOeeeddxIUhTkwAukg0Lt3b7NfeTE6YIJLp3VClFZF+w0PIQoVKmR2yPPOO49mzpwZIhS4Kn4jgM8IigdaWDridmCCcxtRDe2lov0G6aRmzZqZnRKd86GHHuIP0mjY7kEpspcacUxwQWnlDJbDifab/LV7kNxll11GIEoOjECqCHTu3Nn8wcRrXG4GJjg30dTUllPttxUrVlC9evXMzgmi69evn6YocLEzhcDs2bPNPuS2RhwTXKZaNSD5LlmyxOxcTrXf+vfvb9oAydWpU4egKceBEVBB4NixY5SVlWX0IUgpuRmY4NxEU0NbMjmlo/2GyeLKlSvnILrnn39eQ0S4yJlAwCuNOCa4TLRmgPKsUqWKQUqVKlVKu1QnT56k7t275yA5LA7euHFj2rbZQLgRkDXiIGvuVmCCcwtJDe18++23Jhn17dvXtRqgg8qLg/Ply0cvv/yya/bZUPgQ8EojjgkufH1FuUayTNInn3yinE4l4r59+6h9+/YmgWJu7o477iC3n5KplIXj6IGAFxpxTHB6tL0npWzQoIFBQCVLlvTEPoxOmTIlx+LgUqVK0VtvveVZfmxYXwRkjTinHyu31p4JzopIRI537Nhhelf33Xefp7XeunUr3XrrrWZ+8OYefPBBwtMzDoyAQMALjTgmOIFuxLay9tvcuXN9qb11cfCll15KH330kS95cyZ6IOC2RhwTnB7t7nophfYbHgDgu6l+BSxFue6663J4c08++aRf2XM+AUfAbY04JriAN7gXxbNqv3mRRzKb8rdXMWStXbs2YdExh2gjIGvEDRw4MG0wmODShlA/A/G03/yuCb7adeWVV+bw5p577jm/i8H5BQwBNzXimOAC1rh+FCeR9psf+ct5nDp1iuSX/eHN3XTTTcb3WeV4vB8dBNzUiGOCi06/MWuqov1mRvZpBy9cX3jhhaY3h+9CvPTSS8q5b9u2TTkuRww2Am5qxDHBBbutXS9dKtpvrmeexOD+/fvp3nvvNUlOLA7euXNnkpREffr0oYMHDyaNxxH0QKBEiRJGP2jUqFFaBWaCSws+/RLLw0GIVwYx4L3Es846yyQ6LET+5z//mbCoUELp0qVLwjh8UR8E3NKIY4LTp81dKalT7TdXMk/ByHfffUfNmzc3SU4sDj569KitlVdffdWIiy0H/RFwSyOOCU7/vqBcAze035QzcynimDFjcpAcVE8+/PDDGOufffaZEQ/zi2vXro25zif0QgBvuWAeFj9s6WjEMcHp1e5pldYt7be0CuEg8apVq+j666/PQXR2i4NxM+APn6Dj+TgHQAcsSZs2bYz2zJMnD8Xz3JMVmQkuGUIhuu6m9lsmYMHCT0Fi2NaqVYu++uorsyhi+I1rPB9nwqLtzrRp08z2dqoRxwSnbfOnVnCvtN9SK0X6sSHrdNVVV5kdH2QmFgcLVVhBgjwflz7embSA7+6KtuzUqZOjojDBOYJNv0Rear/5jcbp06epZ8+eZufHTdC0adMYNWGej/O7ZdzPT2jEFStWzJFxJjhHsOmXSGi/QY8tLGHOnDlUpkwZk+gwVyN+8cWW5+P0bu1x48aZbepEI44JTu/2Vyr9zz//bHYSr7XflArkYqRffvmF5FfPBLHJW56PcxFwn01t3rzZ7Lu9evVKOXcmuJQh0y/BK6+8YnYSv7TfvEYJy0ImTpxoPEwQwxiZ1Kz78nwchrjxAq6tWbMmrrT6nj17jPdkjxw5YmviwIEDtH79esL8kV3A4ur//ve/dpeMc3g310/5qrgFCdCFdDTimOAC1JBeFaVFixYGweXPn1/bm2fChAmEZQPly5c3ydpKYomOxXzc+++/b6yrwvchPv/88xjIR44cSXhNCC/8Z2dnx1zHCns8rR02bFjMNZBf165dCfNF8Br/+OOPHHGgbIy3MmDf7ruxIG3U76GHHiJ8ocwaQLz333+/8QEfOxKEeOi7775LKEeYgqwRt2zZspSqxgSXElz6RT506JBJCO3atdOiAiACLBHAk185gADwzmnp0qXNOiUiNeu1y6+uSv1GjKeixUvQWeecS90Gj6BPfjxE8/93mD7cdoj+9cPv1KrbE5S/YCGqWLU2TVq9k6Z9c5CmfnOApqw/QK+sP0B1WtxBZxcpRk06dqO/r/uFXlj3C/1t7S80ce1+GrbwG6ratBXlLVCQqt7Ygl5ct59e/u8BeuW/B2jy+gM0dN4SylegIOUvdBb1e+0DenXDQXptw0F67/vf6f0fDtHDg0cZ9apwxVW08Lt99NWuI7R891Fas/cYrd1zmFrcfhdhnrHWtdfR+u07af+xU/Tb8dN07NQfdPoPMogX5AqP3RowlH/ggQeMt0O++eYb62WCR7p9+/YYUo6JmIET6WjEMcFloMH8zHLmzJkmGcyYMcPPrOPmhUWbjzzyCN12222EF+ytAUsC4G1ee319Wr31f7T5YLZxk/9n5xFa+OMhuunOTpQ3X34qe9mVVLVJM7N+VkKzO67+l7bUpEsvqtumAz3x9uc0fs3+HH+DPlxHtz09mh568Z0c50W8x/75Kd3+9Gh6/K1/217vMe3/qNWjz1D3Ke/FXB+7creR9o4B4+nZxd/FXH9i1ud00VXVqdVjw2KujVu1lxq2f5guvPQqatF7EI1ZsStnnNX7qNj5ZSh/obOp2/gZ9MbGX2nO1t/ow+2H6LOfD9OY196h3LlzG1g9O3YCHT6Rc5g+adIkgqePtYZWzxPtA48R3/GINzS3tqHbx0414pjg3G6JgNmT1Tn27t3raulwI9jdDJjHGj58uPGZQLshxf7fj5ik1H/MC/TFjsP00fZD9Oq3B+mlr3+h2/uPocKlSlOFanWp/79W5LyR1+ynB16YSQ3ufpBAFIJ47h/3OjVo/xAVu+Ai07YdweEc4op0Om1BaqOX7SCQnV25QcqdRk2ncav2xFzHNWBTqVZ9Gvj+GvM6vE94p20f6kOFzj6HqtapR+t2H6Ltv5+gA9mn6CRcQyJjWQ48Zwyf7QJerfKS/JxqxDHB2bVWiM4VKVLEuOFvvPFGV2u1evVqevzxx405IavhLdt/pPIVKxn53tG1Gy3432GDvCb8f28JNyCIpkSZcrZk89znP9DAD9bQoI/WmTei3Q0d79zAD9ZSmyeepasb23t3hc4tQogTL30Uzz8xczHVbnk3tXniuRhcQKzFLyhrtFnlarVo7b5j9P1vx40h8sk//jCk5uvXr0/16tWznde09g8nx7JGHN5PVg1McKpIaRhP1n7DJH2qAU/07IaQsPPMM88YHR5E9X/rtxvzV//Y+KsxJzVm+U6qeevtVPLiS+iOgeNibhiDQFbvsz9vGTK6QTbw2HDzyt5dmcuv9i1/N+qQaRvdJ8+jmx58nHpN/zAGty7DX6Szzi1MhYsVp7H/eIe2/Xacjpz8cwiMZUp4DxrfPcX3QJwGJxpxTHBO0dYgnaz9hon7VMJPP/1kvOuJSeuvv/7aGK58+0s2ffrTYXpz06/U8fnJhgdWvkpt6v/e8phOP3bFbnr2sy0x5zN9oz4+c7Hh3VWseZ0xpM10eXTKf9xq+6HxkAXfUNt+zxvzi8M+2WS2OR7O/N8Ph6j3kBFUsGBBuvSyy2yf8J44cUKpazrRiGOCU4JWz0ji5fOaNWvGrQDWZK1YsSLm+pL1m6nU+RcYXlrHEVPNTituSBBY/3+tpGcWbaTxPnpjIn83ts99/n1MvdywyzZyPrjpMuY1qlC1juFF48cRP5KbDmTT7ydOE3T/sFC7WbNmSb+q5kQjjgku5tYOxwkV7Teo5EJhBJ/s23X4OK3Yc5Te/e5346YfvXSH4ek07fooDf90MxOBB0PnKBHhgPdX0zOLNsT0o4EzF1LpshdT/gIFaMToxHNrskZcq1atlG5UJjglmPSLlEz77cTpP2jUy9Mof8GCxtzU8H8ziUWJcIJSV3jRNz3wGFW/pR31f2+FsS4Qa//2Hj2z0HnDhg2GWgzeEEFIVSOOCU4/7lIqsdB+q1ixIs2fP5/wFAph44Fseu+HM17aiC+304339aGOI6cR1mgFpdNzOXIO8aKKx9++3EJV654ROoXgKUKqGnFMcAZs4fona79VrlyZChUqRDXqNTBW5Ef1ZuF660eaWMqDh1i58+ShJu3uoR2HTxrv+Ir1jSoacUxw4eI2ozay9luTW1sZDwouqFSZRn71I3tpPJemVR/Amsl+c76ip+edeVKPNZV/aXGmT+MJf7LABJcMIQ2vC+23ewZPoOe/2EZ4ioWnnuzF6OfFcJvZtNmS/9ElNeoZP9wQGEgUmOASoaPhNaH91vbJ55nQ2FsLbR+4+aEnKCtffmMFQKLblAkuEToaXoOSBK/St/nVZ7ILFdnVanEX5S1QgM4+++yEdykTXEJ49Lv41ltvUbO7OlL7YS+HqkPzUI1JW+4DD788h65r24HuvvvuuOKiuHuZ4PTjsIQlFuqneNJUs/kdTHLsuYWyDxQ578xbNlglkCgwwSVCR8Nr7733nvkS/NlFSxD0y+RfPt5nT0j3PnDj/X3NPi4+GRnvVmWCi4eMxue7d+9udoCzixanB/72FpMce3La94G7Bv+NLrqqmtm3ITufLDDBJUNI0+v4ErhYEIlt1ZtaUdsnnyN+JYs9ON08OKyDq1S7QY7+rEJuuHWZ4DQlMJVi4wMrLVu2zNExQHYXX1WdHn3zE+1/0XW7Ubm86j8uz3+5jTo8N9n4YZZ/qCG7rvqiPROcCkuEIA6Irm7dujFEh8WSLfsMoafmLmGy4yFsxvvAU3P+Q5df25jOK1+Jzi1xXo7+euGFFxpfHMMyKLsvisW7TdmDi4dMyM4fPHjQ+KLSueeea/tVqqLnl6FzS55HTTr3OqPxxjd8xm/4KHh8ECCF6nOd1u2ND+bI3hr28c3b8ePH086dOx3dkUxwjmDTO9Gvv/5Kr7/+uvFVq3z58uX4pRQdDO+u1m1zL7Uf9hL99d2lhK9NQYo8Cjcd11F9KJkKVs8t/s78MFCZy6+hs4uVsO176IP4WBI+F5huYIJLF0HN03///fc0depUKlCgQNzOJkgvK39+qnZTa+OrV33+Md/4wlMqHZzjekMcQcN17Iqd9OALMw0ZrqZd+9KVDW6ioqXLxO1fULtp3rw5DRkyxPh612+//ebaXcUE5xqU+hvCe6xfffUVTZkyxZCRFpLnguDstueVv5TwV+z8snTZtY3okUlzc3yWLmg3H5fHPZKF0nPv1z6m9sNfJrwbig8N4aPWdv3Eeu6ss84yvsG6ePFiglKvV4EJzitkQ2IXcx+9evWiCy64gDDRe/755yt1YGh44atala+/0SBADHlve2qkIX0zZhkPdQNPtPj26qq9hA/K9Jz2Pt099O8Eb+yqRrcQPHkrYSU6xjdB8D3VyZMnG9//+PLLL+nkyTOKvV7fJkxwXiMcQvsgPTyZxZACy1DwwnOiDm53DUOWirWup8vqNqJiF15MIMBWjw0nfOAGXiC+Oj9k/nqe9/PgYQ9kwh/8+yx68O9vU9cJbxIW0LboPYgad+xONZrdRucUL0VYjpEnT1ZK7YrP+pUvX56KFi1KFSpUoP/85z8Z7/1McBlvAv0L8OOPPxI+YANp9AULFtBLL71Ejz76qEF+F198sXGz2JFcKucgjVPumpp0ZYObqU6re+iGzj2pea+B1KRLL6rZ/E667elR1HP6B/TErC9o0IdrCRPa5hfgNf3qVyIvb8SX24yPZj/65iLq+/pC40cBun93DXmBbnrgcSpbuZrxo3FVo2bGIln8gBQuWZryZOVNibSsbVSqVCkqWbIkYYgJRd2ZM2caXpn4ZkLQejMTXNBaJITlmTt3LkFleN68ecYw5cknn6R27doZ310tXLhwWjec9Qa0HsMTwXC5aOkLDfnrK65rQtVubkP12nWi+nc/QIXOKUxnFSlmkGXLvkOp9ePDqV2/EXTbX0cZ5yrXb2p8FOXeZydRh+enUKdRM+i+sa8Zng/mnODxgFi6T36P8HHkh1+abXhH949/g+q0vtfIq8OzrxiLVvFEGkO9OwZOoHb9njMWsSJOy0eHUos+g6l5zwHUrNtfjfywFqzAWedQyYsqUKXa9ansFVWoRNnyhFfvQPbWerp1DO8Lf/nz5ye8yD5ixAjC5/rWrl1Lhw4d0q53MsFp12ThKzAmmfGh6fXr19OiRYvojTfeoDFjxtATTzxB+GhOnjx5jKe88BzcupGjZAcfXcbQ8dprrzW+SoXvkF5xxRVUrVo1w/NeunQpbdu2zdPJ/kz1Wia4TCHP+TpCAJPTIMOVK1caXwobOnSo8erOgw8+SOPGjaNnnnmG+vXrRz169DA+JozlL5gjhIwUJrsvv/xyKlu2LEHPH8QZdKKDBwpPCuTUtGlTat26NbVv354qVapk1AHH8LJeeOEFmjFjBs2aNYs++OADevPNN2nOnDkGcTkCOiSJmOBC0pBcDWcInD59mk6cOGF4LxiCYRH0/v37ac+ePQZBgDBBGlu3bqVNmzYRvlj29ddf05o1awik2rVrV+M6ljt88cUXxjIbLFBdtWqVsQyiW7dutG7dOtqyZQthzeH27dsJy3E+//xzmjhxIr344ou0Y8cOOnLkCGVnZ9OpU6ecVYRT2SLABGcLC59kBBiBMCDABBeGVuQ6MAKMgC0CTHC2sPBJRoARCAMCTHBhaEWuAyPACNgiwARnCwufZAQYgTAgwAQXhlbkOjACjIAtAv8PWEarGre4sWMAAAAASUVORK5CYII=[/img][br][br]What was the scale factor of the dilation?
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
[table][tr][td]If your teacher gives you the data card:[/td][td]If your teacher gives you the problem card:[/td][/tr][tr][td][list=1][*]Silently read the information on your card.[/*][*]Ask your partner “What specific information do[br]you need?” [br]and wait for your partner to ask for information. [br]Only give information that is on your card. [br](Do not figure out anything for your partner!)[/*][*]Before telling your partner the information, ask [br]“Why do you need to know (that piece of information)?”[/*][*]Read the problem card, [br]and solve the problem independently.[/*][*]Share the data card, and discuss [br]your reasoning.[br][/*][/list][br][/td][td][list=1][*]Silently read your card and think about [br]what information you need to answer[br] the question.[/*][*]Ask your partner for the specific information [br]that you need.[/*][*]Explain to your partner how you are using [br]the information to solve the problem.[/*][*]When you have enough information, [br]share the problem card with your partner, [br]and solve the problem independently.[/*][*]Read the data card, and discuss [br]your reasoning.[br][/*][/list][/td][/tr][/table]
[size=150]A beverage company manufactures and fills juice cans. They spend $0.04 on materials for each can, and fill each can with $0.27 worth of juice.[br][br]The marketing team wants to make a jumbo version of the can that’s a dilated version of the original. They can spend at most $0.16 on materials for the new can. There’s no restriction on how much they can spend on the juice to fill each can. The team wants to make the new can as large as possible given their budget.[/size][br][br]By what factor will the height of the can increase? Explain your reasoning.[br]
By what factor will the radius of the can increase? Explain your reasoning.[br]
Create drawings of the original and jumbo cans.
What geometric solid do the cans resemble? What are some possible differences between the geometric solid and the actual can?[br]
What will be the total cost for materials and juice fill for the jumbo can? Explain or show your reasoning.[br]
Describe any other factors that might cause the total cost to be different from your answer.[br]
[size=150]As of 2019, the Burj Khalifa, located in Dubai, was the tallest building in the world. Suppose a scale model of the Burj Khalifa (without antennae) is 30 inches tall.[/size][br][br]To what scale is this model? You will need to use the internet or another resource to find the actual height of the building.[br]
How tall would a model of the Eiffel tower be at this scale?
IM Geo.5.8 Practice: Speaking of Scaling
A baker makes muffins that serve 1 person each. For a party, the baker is asked to make a large muffin in the same shape as the individual muffins that will serve 100 people.
By what scale factor will the muffin need to be dilated?[br]
[size=100]The muffins are contained in decorative paper liners. How many times more paper will be required for the dilated muffin as for the original?[br][/size]
[size=100][size=150]A board game manufacturer wraps its game boxes in plastic. Its most popular game comes in a box that’s 8 cm tall and uses 1408 square centimeters of plastic wrap. The company sells a travel version of the game in a box that's a dilation of the original box. The travel version uses 198 square centimeters of plastic wrap. How tall is the travel version's box?[/size][/size]
[size=150]A cone has surface area [math]360\pi[/math] in² and volume [math]800\pi[/math] in³. The cone is dilated, and the surface area of the dilated cone is [math]2,250\pi[/math] in². What is the dilated cone's volume?[/size]
[size=150]A scale model of an oil tanker truck can hold 1 gallon of oil. If a trucking company wants the full-size truck to hold 8,000 gallons of oil, what scale factor must they apply to the model?[/size]
[size=150]A solid has volume 4 cubic units. The equation [math]k=\sqrt[3]{\frac{V}{4}}[/math] represents the scale factor of [math]k[/math] by which the solid must be dilated to obtain an image with volume [math]V[/math] cubic units. List 2 points which are on the graph representing this equation.[/size]
A cube has edge length 3 inches.
Find the surface area and volume of the cube.[br]
The cube is dilated by a scale factor of 0.5. Find the surface area and volume of the image.[br]
[size=150]A circle with an area of [math]100\pi[/math] square centimeters is dilated so that its image has an area of [math]25\pi[/math] square centimeters. What is the scale factor of the dilation?[/size]