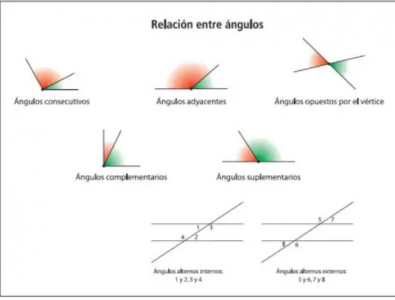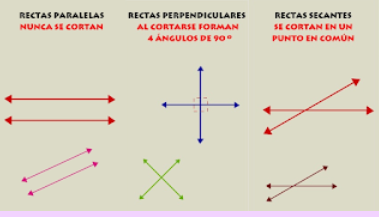
Rectas y sus tipos
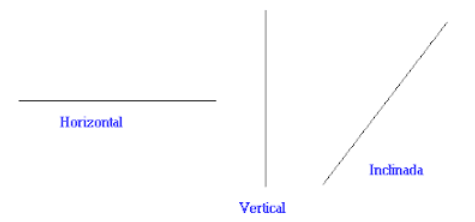
¿Qué son las rectas?[br]Una recta es una línea de puntos que no tiene ni principio ni fin, que se extiende en una dirección específica.[br]Existen diferentes tipos de rectas según sus características y orientaciones: [br][br]*Paralelas:No tienen ningún en común y siempre mantienen la misma distancia la una de la otra (son equidistantes). También se caracterizar por tener la misma inclinación o pendiente.[br][br]*Secantes: tienen un punto de intersección. Pueden distinguirse dos tipos:[br]Perpendiculares: Al cruzarse forman cuatro ángulos rectos, es decir, que miden 90º.[br]Oblicuas Al intersecarse forman dos ángulos agudos (menores de 90º) iguales y dos ángulos obtusos (mayores de 90º), también iguales. [br][br]*Horizontal: Es aquella recta paralela al eje de las abscisas (horizontal). También se puede decir que su inclinación es 0.[br][br]*Vertical: Es la recta que es paralela al eje de las ordenadas (vertical).[br][br]*Inclinada: Es aquella cuya pendiente es distinta de cero. No es paralela ni al eje horizontal ni al eje vertical.[br][br]

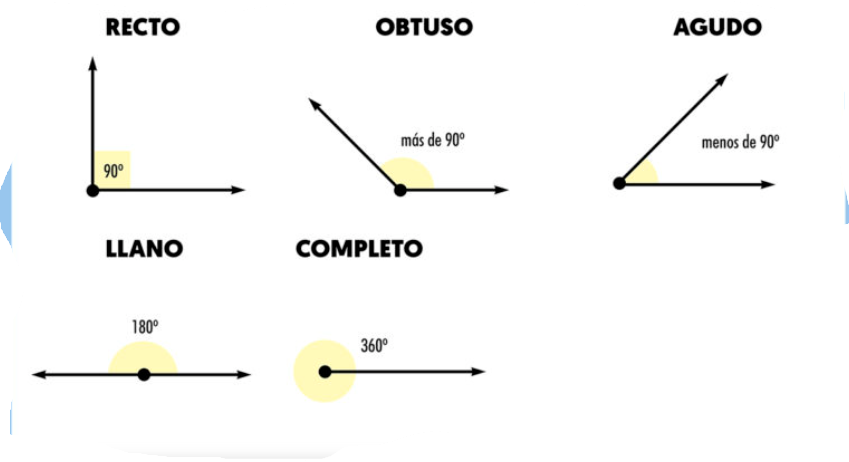
CLASE DE ANGULOS
¿Que es un angulo?
Un ángulo se define como la figura formada por dos líneas con un punto común, llamado vértice. La medida del ángulo se expresa generalmente en grados[br]Existen diferentes tipos de ángulos según su abertura y posición:[br][list][*]Ángulo agudo: Mide menos de 90° y más de 0 °. Los ángulos agudos son más pequeños que un ángulo recto.[/*][/list][list][*]Ángulo recto: Mide 90° y sus lados son siempre perpendiculares entre sí.[/*][/list][list][*]Ángulo obtuso: Mayor que 90° pero menor que 180°. [/*][/list][list][*]Ángulo llano: Mide 180°. Igual que si juntamos dos ángulos rectos. [/*][/list][list][*]Ángulo completo: Un ángulo completo es aquel que mide exactamente 360 grados. Es la vuelta completa alrededor de un punto y se utiliza en geometría circular y trigonometría.[br][/*][/list]
Ángulos complementarios: Dos ángulos son complementarios si su suma es igual a 90 grados. [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAQ4AAAC7CAMAAACjH4DlAAABZVBMVEX///8AAP//xf/09P+U1JTd3f/h4f/r6///AP//x//z9PwAAPrh1//rtP98tp6W15MAkwD/y//v+e8AAAA/P/+lpf/W1v93d/9ycv+03bTT0/+urv+pqf9vb/82Nv/Pz///m/92dv9BQf//0f//9P//b///4P//P///r///5v//d/8AmAAAjQD5/fna2tkAAO4AANcAAIIAAHYpKQAAAIzv7+7/TP//K///vP//Q///1///Xf//7v//uf//qv//hv/X7dd/rqfGlPmSy5TB48GZ3I26urWZmY8pKRgAALcAAGUwMBcAAMkTEwCDg3kAAKAoKCEUFCI8PC+np6JMTDwAAEwAADcAAB4AAEGtrZ4AAFVHR+UAAAUvL///g//rGv/rhf9qAP+ExoQ0qTRiuWKWbvgAYHWw3aVVs1VmRflPYdolpiVnib9OsU55yHkZGQCxg/lgvVxvb2IuN+BVpHgAgSogjkefGhlFAAAHF0lEQVR4nO2di1cTRxSHNxuEDdGaJYCCD6IkhJBEIAJRHhIaBEGFFrC21kcLtGqt9N2/vzN3NhkmySbR09mZ2dzvHJM9nN3Z8TvzmzsDmxPLQhAEQRAEQRAEQRAEQRDC1vb2luo+aMOdR6Wdnd3Hd1T3Qw8Wk08ihCdPF1X3RAv29iPAwp7qnmjBV7NMx+xj1T3Rgq/jno5HqnuiBQfe6Jg7Ut0TLTjcZTpeHKruiR4czVMbJRwcHnvJ3d0k1pU6/XNzA6r7oBH9kQjq4KAOAdQhgDoEUIcA6hBAHQKoQwB1CKAOAdQhgDoEUIcA6hBAHQKoQwB1CKAOAdQhgDoEUIcA6hBAHQKoQwB1CKAOAdQhgDoEUIcA6hAwRcedrUAefjVDx9bTZ6Vvgnga2AgdW8/pM31zSfk+TNCxmGQPfM7dlX4rE3QczrMHHCPfSh8eJujY3vF0lKR/uMIEHd8teDpe4OiwrNHvX3rPiiel30t7HdErkcg8PB0dfyn/g0i667hOPNwc304u7JeSAXwsS28do8PExgg5WDwM5jNqOuuI3iIybkSDvKXGOq4RGcMTwd5TWx31nASKpjpoPYlcDb5neuq4riAngI46Rm+ryAmgnw6Wk0DrCUc7HWzdperumulQU084WulQVU84Oum4pjQngD46xtXVE44uOpTWE44mOtTWE44WOlTXE44GOhTs431RrwP2JxrkBFCtQ4t6wlGrA+rJDdVpPYdSHbrUE45CHaM3iY3rim7ugzIdg1f1qSccVTo02J+0Qo0OHXMCqNAB6y71+5NWKNBB68mr0YBv2iWB6xjXNSdAwDqitJ5cHQzwjp9GsDpG9KwnnCB16J0TIDgdAzQnV7SsJ5zAdNB6clvnnAAB6ZgY1j4nQCA6ojcMyAkQhA5aT4Y1XXc1IF+HAfWEI1sHrLtumZATQLKOESPqCUeqDsjJNWnNS0CiDrbu0uj3wl0gT4dB9YQjS4cp664G5OiImrA/aYUUHabVE44EHYbmBPjfdRixj/elhY5JyjI5SE+nbPqDdGbJ7rY9I+sJp1lH2gEsa8pxVpxs2rKWpnPlqa5ag5wYte5qoFnHlDOZJlhWtkxeyhnLImpS0120Zc4+3pdmHWsOe59y7pFX20lbKynXyXVuakSn51Y+k2Yd6/fdmXWSjUmHBmTZmSQ/yix3bGj8leE5AZp1LDnZ9fvOtJWD0bHmdDWLhiAnQLOOldfkZcZZJV5yxAlI6QSsu8ytJxyfdUfOWbNWy6TAPHDcjm1MGLeP98VHx6pDS8mySybUTiV2kObklr5/Z/wkmnTkQMQkmUFTVETK6dAA/J3xgqzuBU3z6GDLjSz5t0TlpNpeHo56wiE6GuoBmT2zTjlHa6xTdjLtLmb1JCQ5AYiON+VsJmWfmyLsB6y4ptcetF1vwLorNDkBLhIdbJPizKytfsqVIaonHKLjh/WZlSwzstLNIgMYCMm6qwGi45LrujF7en0JjKS6uiyEOQGojphNiMVcO7XUnZBQ5gSo6wAl7r0M8VGOtb1kIHT1hCPoIDAhmbT/FaHZn7SiUQcRMn2fCJn0OZ/mJB7KnADNOkhk1unerdXZIa0nnBY66AAhm9mZ5pNDnROgpQ47Zq84TevziZDtT1rRWgcZIJkGH6HPCeCnA3y85ufRnLwPdU4AXx22O8PnU5qTENcTjr8O2yXzByzIeiMnQBsdtk02dumeyQnQTkfsHim3wvNdxWL9QnZU2VTQZ4m0HR1u6s2P5/cnx/nEhzF2WMkPkdfqyemJqp5Loe3osH+i6676Pv4ssTlULcB4qOSpjmKe/DBU48NfR8z9cpbUk5/f1k4tJqrk9eSUHFUTH5iOIetdb+hwL70nQ+OXd/l8fb6AmYPqqCTGxhI0LJv5D2fq+i4BHx0u5OTmxsPLeRgTHsXKWb5C3oYspoMehYqWOryc/Hr5cl/fu0Senz1WKJyyweLpCButdHg5qT7sI5DhwWeHYrGSZ6WkZ3TEYrWc9AEniY/nL9gsVOhbj+io5aQmo6/vLOH9z4eq9L3CKm1v6BBy4pFPsKXXUIFOqsfMQy/oaMwJ42PilJ17XKhWjgtsHTJWCLsOkpO4mBPGab22jJ3kP3rzauWs6NumwXAdrXICkJ1KRXU3g6Kmo3VOapNHqBbi7WA6WE4iTTmpldq3nRsKB6DDNye1uVSvjcnh4+TdbTlNUx2wPxne8JFB1+mncm7+eRzMz0bi+78tymib6PjdW3f58kdep9/x/LkPX9by5EhG4xeh7b82vmjD3//8239BF/qfe1/l80zGV/mMQ9PxiDHslLyDfRnTx0Ak3gVKBYjs7HoH+4cSdFiD0cHORPVh0PuiJzlhMY899j1gO1KmUgM5Ks3Nzi4cSCm0JrJ1dHAkZeJAEARBEARBEARBEARBEPP5DxUFucvoSHK+AAAAAElFTkSuQmCC[/img][br][br]7. Ángulos suplementarios: Dos ángulos son suplementarios si su suma es igual a 180 grados. [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAR8AAACwCAMAAAABtJrwAAABXFBMVEX/////wP+k26QAAP8vL/8kJP//w/8kHf8bH/On354VJO//xf8AkACp3qn9/f//AP//Kv/Gxv/x8f/39///Of//rf//ZP8AlADLy//u7v+Jif/j4/+vr//Y2P96ev//ev//0f9/f/8+Pv+bm/9NTf/o6P//lv//h///4///3P//jf+7u///Tv//bf//8///Xf8AAN5fX//S0v+oqP/p6eYAALQAAOxGRv9ycv9ZWf//7P//qP86Ov//tv+73rvQ5tB+w35juGPs+OyQ0pCUzZR1wHVNr02v2a+Vlf+QkP8AAJAAAE0AAIXGxr9iYl7s7OmqqqMAAFoAAHDV1dFycmpUVFiQkIUAAMsDAz8nJ0EAAGOXl+RmZv//n/9EgZ2PFvwtpi10k8mLZ/fO6c5risubcvhkgc+wgvlfedJXQVtjS1mheZhZt1lWckIqKjcAADWIt3woKNAHEYM+PkNSkkquAAAGsklEQVR4nO2d/VfaSBSGE66QdYMaTCQIIioiiiB+UuonpIhVi63VurZbd9N1v9vtbnf//3N2ElCsJRM8JcwcuM8PUXJQ37y+cycJmRlBQBAEQRAEQRAEQRAEQRDEGyZWVh4XV1mr4JfoSiS0BnHWMrglGrU206xlcAuxRh3dDrGWwS1R8Esww1oFv0Snh9Xx4gprGdxi158YDLPWwSu2P8kB1jK4ZRoGBiTs3x0ZjcViKWxdCOIZ67Xac9YaOObF6cbG6QvWKril9hIIL89Y6+CV84LlT+GctQ5eeQU2J6x18MrFsmXPdxesdfDK80vSwAqvsQdzYv3Vmzen37NWwTXDACprDVyzBknWErhmWMJbQFQwQHRUANYS+CYJa6wl8A1gBaKCAaIzDBIGiEYSJlhL4BoVJNYS+OYpBogKBsgFDBAdFfysJfDNISyylsA1KuCTClSiGCAqoxggOtMYICoYIBewAtEZxwDRmQZ8GprGOD4OTQcDRGccHrGWwDeTGCAqKQwQnSJEWEvgmhh2YXQwQHRiMMtaAt8UAcfs0kjBY9YS+KaIY56oxDBAdN5igKjEMUB0VjBAVDBALmCA6MThLWsJfPMYYqwlcA0GyAUMEJ1VDBCdWQwQlVUospbANxggOhggF2YhxVoC10RgkrUEvnkE46wlcM1XBWi+D0ZFb7ddgRJj1jYsk01W0ZQdYS6R3fROGCeEoM3ZNdMjlj+5EeLP/MjU1NSmkBfkLU+1ccF2exVIy+WJPyNpLSAIYt7elU73QX7aDdC8EB6ztpY/GU0ZSZB9C0sea+OCGRht631hu/5Y/qQz5GvGU1EcsQjRtt7X9MdCVDwTxBvb7c1e0vQnQ8qOqHkriiMW4bD5YmmB9E1TCy0Kb9OfLCk+2ly35LFnoF6BNsW5vHJLNj228Nm7cjvWNkv696XsiF2f+wUrQJtbYY2Ykkuk5wiZRC5rvbxaaP0TS33Rc93ih7SmaLmrHVGWA3XkwM5Wgpwn52TW4thz/QP8mL8S5YD4GcSlsZymhKdY62NMKagXQLxnTsMiWUwrSqIfWtN1ZZdsjT0CsWS/uV8Pmk/ewU9yK38I8k5O0UR2urtExTyolgXBNKvVklC63is19vt0vTzk8/nBwR7LoS1NSff45CaGTjamIOj2q6Y/+yQ8xJ7Bd/CLU4BIKxNzSri329hBWdgl7cowd0vX5GWpZNi7y0HTR+whSJQAkQgllGxPG1QxzZJeEXaDlQPy5YZysFp3xyVAxKCMku9lgyqkYRlBwyAZ2tONxs79W3sIQA2QKM8p+R6+nTpUJRvTalqkFDX8GSKN65bBn+kBshKUZngAHrNnFWbdKJUb39q7dN9dXAIkyjlljOkxeMqH6i7p3w29sqsf1PeY+pMh3wMCJIpZbZ7tQXjJwb7li1Gx+y/BOmsuD/keFKDAmBJmegjdxNDNe/YM/uoWINLL77DW3S3KeumeP74hgJYXYXfQsqx1d4m9L+JjB+g3eoACmX4J0L7+5L49doBc8hPQ8qyVdwUj+GV82gzQFGvt3cAX3G/hD+nCJJcA7fTySWITU2/ljm/wd7cAyXmtly/DGhh3L7zucuAWIA4a2LD3Y2d3HZqXe4DIOSLrD77WvJ8foxRs0XvdBIh+DhTIsu7Btp96PjKrqreOTxsBksOaV7daYxORNn51HATPnwk0W/XuNwECWaY4FEgo3lykqrPS5Lbk/jDbZFKYvPk8fP3i5Hy981IM3aE82wHa+OPP9xR/5pQOfmJ4dn5y0Vga6JH1IOSh6+xoKsTVSGMu/bPLZSgc1zonp4Ghf3D0x/fXEcDGa2d/rjp4iVE7LcDypZ2AuP0Qibrmdo9yEfySv1GhP9pLd/3dMTk37OnVQSf+ObL+5vL7m8+Z7yOPddCfY/sAP1rfTrQ5p8ystcxA0p4/ZP2Z/eNHnwY6zbfO/GuvFwbHkiMgdUrGJ/t/AS+tFjbR3pQpKbs2p+xxI7f++DvNN474n7n6I3VMxl1/IvXJzUMu7StUL82H9iyXXrUvGmfPurje3GWzfQ3bw6njD+q6z46XYdmD+kzl4qhQ2PivO3+r9sY6wPramhOwGAs9cBkl0r9fdH1lztr5SdeWS7UO8OYEJjTrn8EJ8hEEQSioPf4s1NcRmZGktzio0IkQLKrjUVwv1Yn6pXGxzUFzfUe8fmtlFZe7bE2ovoRRCv1pzWr9MjqO/rRGrc/IkcTJ2xxI+ketUfE4d5sTT2HGjzPUU1BXMTwIgiAIgiAIgiAIgiAIgiAIgiAIgiD88T+l/rhMVUeZ6AAAAABJRU5ErkJggg==[/img][br]8. Ángulos adyacentes: Dos ángulos son adyacentes si comparten un lado y un vértice común, pero no se superponen. Los ángulos adyacentes pueden ser complementarios o suplementarios dependiendo de sus medidas.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAARQAAAC2CAMAAAAvDYIaAAABmFBMVEX///8AAP//nP+Iz4j/AAAAAAD9/f/Pz///AP/1+faK0oZppp3/oP+GAAD19f//n/8AlgCAAADs7P/HmqBtbf+urv+5ubmiTln89ve/v//u7u7b29v37vBUVP9paf9ZWf//kv/z5OewYm/k5ORzAAB7AADmz9OBgYGysv//zs7w8P/t6P+5e4SeOUqWHDTPz89NTU3PpazXtLqeRVHgwcb/1dWbm///5eWHh///sLAaGv8oKP//N/9sOv6PACI7Oztra2sdHR2Rkf/Z2f+MABbGxv+Kioqamprl1db/wcH/oaH/h4f/Wlr/QkJ2dv//fX02Nv//R0dAQP//bW3/kpL/GBjf3///fP//UP/P6M/CcP5bTf+N1n92x3a1cnuTDisqKipubm6lpP//MjL/3P//0f//u///r///6///c///RP9tAP/AAP//ZP9zRv4AbGVeulGdWvwuZLI2TN7fhP11vXV+vZGg06A7rDtdiLlHZc8uPeO33bdtoaiCw4p4sphVfME9WdhEr0RjkbKWVvwvimsAd0hFRUXCgIW9AAAMlUlEQVR4nO2d+UPbyBXHNWApG4IAx4ktsBIsE8sctkGyCMF0HQiEmJCQcIV02TUh5G7Tprs90mu33V7/dt+MjA/wIckzOog/PyAcY2n8zXznvZk3tjiuR48ePXr06NGjR1AZm8VMeN0MfxHlCXcve90QPxHl766vr9/l0143xE9E+WX4GefnvG6InwBRxiYm0vwDrxviJypjSq+j1BPlX6TTx3eJiXpUMMcUjufjHjfET1REWeFnPW6InwD7HB+DfVYEr1viIyoD7UrPPXVcnsCMed2ML4JIvvFx6ZY37fAVkVjjYyWgokzTPNlFEeX+dYonw6LIWiYiw+8SHNVbp79QvIgLCOglvZNhUWJJLbkmcUI+q2VyKRCpGNMyYZ3eRdzgDrpH7VxYFAWOosFpOThq0FOSZfjFSAUrIVpFaIvWuUz7lPMgSl7jzDFFJNZJBcxATxG6SelUIIoilnUlZ3BZbBgQRQqX8DPhgIlyGyG0Q6d3gygaDkDQU5IZOBrQU45wl5FvyVQu4BozIAp6OkTjVCCKLipSOWxwakqXVDzQ6mFDUrJlGqd3k0OsSmGGwplwRpsMi3oOvKMVw1kDROH0o/BahsLJ3eU6Iqx63Q5fMW2Kgu573RBfMW6KskRlXLkojBJN7gUrv2IOa/dIErtzM+Mauj2OCszcI4sl6ucUZqNRtotkq5dwtnKN1enz9KeDs2Q5lXktDwLzKKNTK9TPGOf5dHSd56PUz3yGGwg5NpCsRXQYpxU44EcRTosonBLRYCxR8b/gH5pSimiUBvM50kke8Md0Tteaq84nhqoYy+RUThPLmVxW4tRwLBMTtVwml6us20ayHFeM5TNH+Y7nsoLA83g8EVyIl44NJKzhSZ8kk/WBXATmPfBLLCxx0q2SuUSJlcnhxZYUFStN8DyN01hi3KGB1DVy0LP4p5aFngLHTJIjKwZVUYrYR3TikJuiODWQqQYXSZIHuYooeGJ8VhSBUnDmebw1Lb7sRtXXoYHUMEnODNJhQIwGUTSsWIayKMtkiF12Z9eEwwiUTcqcoXDFjCQY4VKjKKWUIahrMbqijPH8XHrO7C/MueoshZNjR7kcxOA8HAyOK4lcRRS8QJsp5mLYQ/gZoUgpt52Yw/sYXSqFM0zhKDMWd2/H62EXKdyFxaGB3IVepcoi/jfQTGHS9Wt2Mwdyg0m05P5FGRlI2puncRphCyH3OworAz0MhRa6P8vqEkJLnqybOp0DtUXeD+13XSZ8iddNaW4esU4XiwhtWAiFtrs7w9BNUrbzaIGdjYE2QqHdbl6/WiAL7LdptccubCIQDCubzl99u1Kz8yw0MopAT0KhRaevvVfRxPXErQajFO5RKDTl9LWVnkJ156JNGKVwJ10EZjKk3KHZGrtMszGQHArtOywXwn8TJClX6bbHJowMNB8KPXb0wjuQoAztUNue55BDNoVUh4H5OnGO4G1HYbeIAIF5z/aLLiE0zqAt9mG1iOAgMM/Q2pXXPTcY7USwHZiFpwg9Y9ESBzBbhbMbmMf9tPeMlYFsBmZIZil+gKBrmCwicDYD8yTFjfI0YLOIwJHA/Mjin64idINJGxzDbBnb8owZUmt2G88cwspA3Ka1wOynwFOFmYEsBuabfgo8VdjVgawE5nserrS1g1kdyEJgHvVrvZJdIXW+01I2BJ4dNpfuGnYGMmfMUqsq2VABFbxcaGsLu0IqnjHLJ63yuEM/f96G4U4EmDGHWkUhjwqkVmG4E2Ebi9K0q9z2dOXeAswM9DDUqqvcZ5Yg0YKVgTZMTZoEoWfUPgLLDlYGmtpv3lUg8Hi8cG8FVnMgabdpVwG/XmJxObqwmwMtNukqd7zacGETdhFo4fHZrnLd40qgdcBArEa+zcau4pt6RmfYGYiMt7WuMuPVDi4nsNxMCuPtaVcRlhCi8R0DLsF0M+niaVo7HojAU4XRToQKC+aK0x1/1TM648JubL/VMyzAfDf2KkKHTC/AANYfZ5gO5NdQMDaQH+sZFmBWB8L4s57RGZYGuu3TekZn2BnIt/UMC7AykI/rGZ1hNAeaLvivkG6DSSYG2vFzPcMCLAx00/cfXezANH0DBTfwVJmknU8EOfBUoTwHwttkA7Os1BK6iwi4nuHbQroNqKZwvi6k24GigXxeSLcBPQO9DEw9ozO0DHTfd9tku4FOCheoekZnqCwiDAWrntEZGnOggNUzLNC9gYJSSLdB1wYKTiHdBl0aKECFdDt0tRPhaiDrGZ3pahHhogWeKl0YyFcfDKSL4zmQzz4YSJVmcyDp1es3wwnM29ev3jV/XQAL6TY4Y6ChN4kPXzVy8PbVuVcFup5hgbovl3/35uOpEr8gVB8lGnXx4wcDqVJN4d4dmAI8f59I9A0PYvr6EgcfTWk+vKm9RNgJZiHdBqaB3r0ninxMDA4OD/fVAHX6Dp6T596eviLw9QwLgIFm+vDbfp4YrNejTpi+A9xfPrwmf38B6hmdAQP9Ct7yx77BZoqc6nKAB+D30gWpZ3QGJna/ft5OkoosuDe9enbBA0+VQ4T6mhqnUZZhHJyWLkY9ozNgoK87dBTCYOKrwoUPPFVeIvSNJVV+g9BvP3ndWrcAAyUsaPI7hL4fGfnZ69a6hCUDDX6D0A8Dn0ZGvvO6uS5hwUDDv0doqX+gH1T5g9fNdYmOBhpOwCD7x4H+fqzKn7xurjvMdDTQU4SuYE36+z+PjPzS6/a6QwcD4cDz52/7TUZGRi573V53aGsgHHj+cqpJ/3dfzLDSzkA48Px1oL/Kp56BqoGnxueRz1431yVaGwhVAk9/nYH+5nVz3aGVgYYh8Py9QZMvqas0N9Dgv+sCz5fXVXAd6JyBcOD551lNcFfx5xwo0ngfcKP7m5A2MRAJPOc1wV3FjwFIzdW+UgzfJyOW7f6c5wyEA0/hx4HzokAG19/99aij1+4faRwJlO5rfC4CLSH0UzNNIFfxz1Ar47cuKFgEWSCPBVnSjhQZHpPnFfIHssN7rJwx0PDXCP2riXl85p8YvrNkpMgJSVEsqhyXy+TEpLgmZrkyvv1oTBRFhVOLoph0tvekwUA48PyjuSbYP76ZLBsi9ISsRiTQihKXLSrYPhy5H6l0VJY4VVZEnZOyEWcX2KkZCA+yTQJPhZ/9s9okHOlcSZRlUZUkBboKee86HlNAFL1IxpVIFixFbkvqgNoq3CAMsjtNx5NT//hmrpyJ4bevpMJgFNHAnaYmSkWIMn5KdCgKrgMRAw0nILtvGni8EGWs7T3bS6KSUzk5XIk9FVEkUxQzKpMb+zqnEoGGC60Cj8mAmyPtWId7tufL+K1nceamVEQx1kxRSjCYQDwyYKytBKMOSM2+U9aMQG0CT3WkdS/Tf8DzL9o9r6XwMKKuZctZfCdWLIpczJe5MvQPTYwljxTwTzJZNCxcayF0srlxLr8hEQgCz/dtNYFM/0dn77AdQmFrssl3xL3gX/Dt7q8s6WZCousGvB2D2EjRVU5VyS8kp1P1amq3QJBlSWqS3S2Y39O2N9/41CEqwIznh28H2vKZSU6L7wP0dGu0cevlLL8cpXh/5alQHfv7Jycnj7e3H2F2d3ef7Faf2V2sc9IMuRHclQ78579XLtGnciMtEGayVrU+5qOV+9lTYT5kmf3djdNXvUS+YOnaJNlHJuHbtqfbD7XtUJQz/yBj98wDU1MbG4uLiw8fPtzb29x88gR6yu52nSaP9qZqnWXcaz0wMLw8I3l5lF9ZXp7jV5xqsqba+fP5qnnOfivz0GULCNThhJogtWHlLm/i8Fb2ec3Wn8OIs725UR+8hXicmnWdgEVZ2hpt2AQT51ewXg+cDrVnzdOBhTPfmiqk8X/IsoeyCFuj5yLyMb+OD2Ot72Uv6REN/msVLaJDHJUish5R4ZEGcqi4m6iQv2mKGtGcLK/M8Xw6/YJf8bSznGM2OlY5thClVMxnwCO6mMxkszKniLFyUoxkM/mizEVyHEdS/Vw+ljnK27961JRjjk87fgOeQNJ7Scb5vABprCJCelsOq5xU1M2pDxElhudI9teZ5syoF3c8znuDEiZv1RDxTz0HooBtNDIZ0upEAR9JRfuiVFLpMYp5khuoRA1OL+KfxpHQWhR5zYkocXwImiiKuWSgkg4TyTf2FA2PKZkuRPkfH8WHCZ73zfKRJZJZBU/9sjEJPGQ0iqKGdc4o5p2Lss7P1R2Cg1QOpyBrlZOpFAytnJICUUjUycGIGwmnYhl4sIZFcTDQgm+W4/F1x6njxWTWTKejXrfDXwjRdPpBoEbZHj169OjRo0cPv/F/lmiMdi77kHYAAAAASUVORK5CYII=[/img]
VIDEO EXPLICATIVO
TIPOS DE ANGULOS GEOGEBRA
RECTAS EN GEOGEBRA
CONCLUSION
En conclusión, la relación entre rectas y ángulos es muy fundamental en la geometría así también para la resolución de problemas geométricos y matemáticos, así como para la aplicación de estos conceptos en diversas disciplinas prácticas.. Así como existen diferentes tipos de rectas y ángulos dependiendo sus características, abertura y posición.
REFERENCIAS BIBLIOGRAFICAS
- Alvarado, M. (2020). [i]Tipos de ángulos según su posición, tamaño o la la suma de otros ángulos.[/i] Luca [url=https://www.lucaedu.com/tipos-de-angulos/]https://www.lucaedu.com/tipos-de-angulos/[/url][br]RAVE BUILES, José Camilo. Propuesta metodológica para la enseñanza de los conceptos básicos de geometría (rectas y ángulos) en la educación media a través de su aplicabilidad en la resolución de problemas. [i]Facultad de Ciencias[/i], 2017.[br]López Altamirano, M. E., Tercero Delgado, V. D. S., Hernández Dávila, A. D. L. Á., & Guido Escalante, N. H. (2003). [i]Didáctica de la línea recta[/i] (Doctoral dissertation).