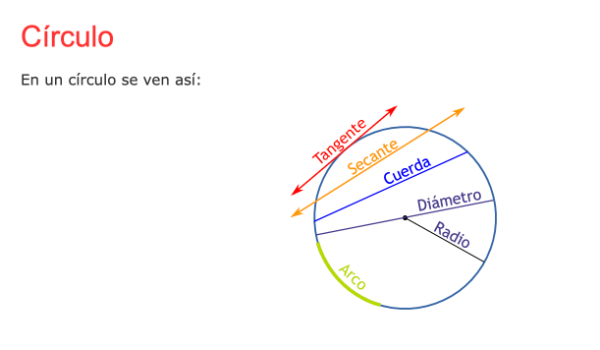
Pendientes
[size=150]Para entender de forma gráfica las partes que componen una función en el cálculo de las variaciones, es importante comprender los siguientes conceptos.[/size][br][br][size=200]Pendiente[/size][br][size=150]Inclinación de la recta respecto al eje horizontal (eje de las x tambien conocidas como abcisas)[br][/size][br][size=200]Recta Secante[/size][br][size=150]Intersecta dos o mas puntos en una curva.[/size][br][size=200][br]Recta Tangente[br][/size][size=150]Simplemente toca una curva en un punto[/size]

[size=150]En la gráfica siguiente veremos como se visualizan las pendientes rectas secantes y tangentes en una función.[br][br]La recta roja es la recta secante porque pasa por los puntos A y B., corta a la funcion(color verde), y la recta azul es tangente porque solo toca un punto (C) en la función.[/size]
Ejemplo de pendiente como recta secante
Responde lo siguiente:
Intersecta dos o más puntos en una curva
Responde lo siguiente:
Toca la curva en un solo punto
Responde lo siguiente:
Es conocida como eje de abcisas en un plano
[size=200][color=#980000]Variación Promedio[br][br][/color][/size][size=200][size=150]En la siguiente gráfica se visualiza la variación promedio de la función:[br][center][/center][math]f\left(x\right)=x^2+1[/math][center][/center][/size][/size]
Cálculo de pendiente
[size=150]La [b]pendiente[/b] es la variación promedio entre dos puntos, y de forma resumida se puede calcular de la siguiente forma:[br][br][math]m=\frac{y_2-y_1}{x_{_{^2}}-x_1}[/math][br][br][b]Nota:[/b] Esta formula aplica cuando ya se conocen la coordenada de ambos puntos en su respectivo eje (x,y)[/size]