Using GeoGebra to Differentiate Ss' Discovery Learning Ex's
This book illustrates several examples that illustrate how teachers can use GeoGebra to foster active, student-centered, discovery learning through a variety of differentiated means.
Table of Contents
- Vertical Angles Theorem
- Vertical Angles Exploration (1)
- Vertical Angles Exploration (2)
- Vertical Angles: Quick Discovery
- Isosceles Triangle Theorem
- A Special Triangle & Its Properties (I)
- Isosceles Triangle Exp: Ex. 5A
- Parallel Lines in the Coordinate Plane
- Parallel Lines in the Coordinate Plane (VA)
- Parallel Lines in the Coordinate Plane (VB)
- Parallel Consequence? (VA)
- Parallel Consequence? (VB)
- Special Pair of Lines in the Coordinate Plane
- Coordinate Geometry: Quick Investigation
- Perpendicular Lines in the Coordinate Plane
- Perpendicular Lines Investigation (VB)
- Perpendicular Lines Investigation (VA)
- Perpendicular Lines in the CP: Quick Investigation
- Slope Triangle Rotation (VA)
- Slope Triangle Rotation (VB)
- Coordinate Geometry: Quick Investigation
- Exploring Slopes of Lines: Ex. 15
- Inscribed Angle Theorem
- Inscribed Angle Theorem (V1)
- Inscribed Angle Theorem: Take 2!
- Inscribed Angle Theorem: Take 4!
- Inscribed Angle Theorem: Proof
- Proof Exercise: Inscribed Angle Theorem (Case 1)
- Proof Exercise: Inscribed Angle Theorem (Case 2)
- Proof Exercise: Inscribed Angle Theorem (Case 3)
- Distance in the Coordinate Plane
- Distance in the Coordinate Plane (With Hints)
- Distance in the Coordinate Plane (II)
- Distance in the Coordinate Plane (III)
- Parallelogram Theorems
- Parallelogram: Theorem 1
- Parallelogram: Theorem 2
- Parallelogram: Theorem (3)
- Parallelogram Construction Template & Discovery Lab
- For Ss Who Need a Challenge
- YOUR Linear Speed?
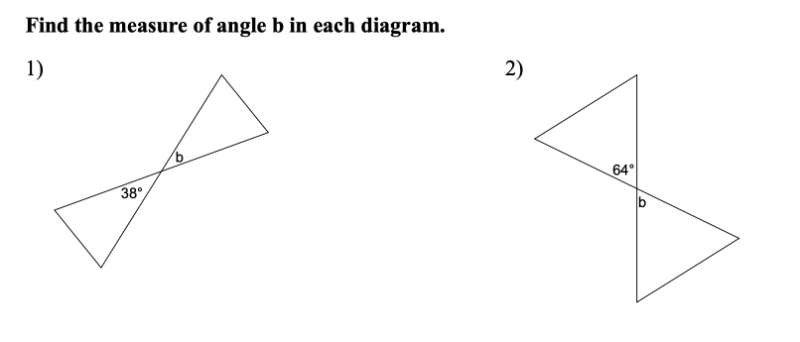
Vertical Angles Exploration (1)
Interact with this app for a few minutes. Be sure to drag the LARGE POINT around and be sure to move the 2 sliders you see.
Notice anything interesting? Describe as best as you can.
What happens if you make the size of the [b][color=#ff00ff]angle[/color][/b] BIGGER or smaller? [br][br][b][color=#ff00ff](You can change the size of the manila angle by using the manila-colored slider). [/color][/b]Does your response to the question above change? Why? Why not? Describe.
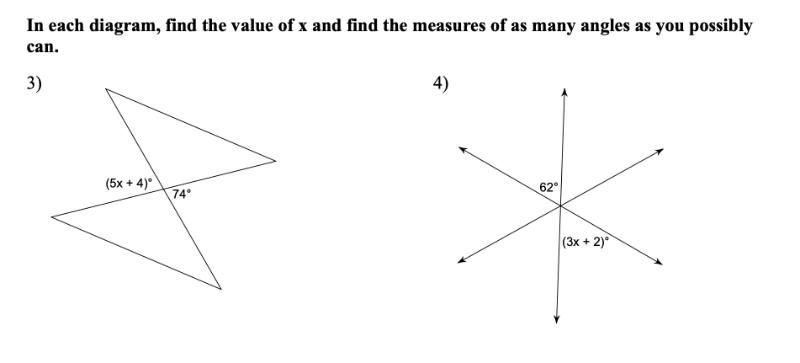
A Special Triangle & Its Properties (I)
[color=#000000]This applet accompanies the [/color][i][color=#0000ff]A Special Triangle and Its Properties I[/color][/i][color=#000000] activity sheet given to you at the beginning of class. [br][br]Use this applet to help you complete this activity. [br][br][/color][b]Note:[/b] Feel free to move the white points anywhere you'd like at any time.
Quick (Silent) Demo
Parallel Lines in the Coordinate Plane (VA)
In the applet below, lines m and n are [b]parallel lines[/b]. [br][br]Interact with this applet for a minute or two.[br]Then, answer the question that follows.
1.
In general, what can we conclude about ANY 2 (non-vertical) PARALLEL LINES drawn in the coordinate plane?
Quick (Silent) Demo
Perpendicular Lines Investigation (VB)
[color=#cc0000][b]Students:[/b][/color][br][br]Please use this applet to complete the [b]Perpendicular Lines Investigation[/b] you received at the beginning of class. Note that line f and line g are always perpendicular (intersect to form a right angle)! [br][br]Note: The [color=#1e84cc][b]BIG BLUE POINTS[/b][/color] can be dragged anywhere you like.
Inscribed Angle Theorem (V1)
[b][color=#ff00ff]The PINK ANGLE is said to be an INSCRIBED ANGLE[/color][/b] of a circle. [br][br]You can move the pink point anywhere on the NON-BLUE arc of the circle. [br][color=#0000ff][b]You can change the size of the BLUE intercepted arc[/b][/color] by moving either of the white points. [br]You can also adjust the circle's radius using the [color=#666666][b]GRAY POINT[/b][/color]. [br][br]Answer the questions that follow.
1.
Without looking up the definition on another tab in your internet browser, [b][color=#ff00ff]how would you describe (define) the concept of an inscribed angle of a circle? [/color][/b]
2.
[b][color=#ff00ff]How many inscribed angles[/color][/b] fit inside the [b][color=#0000ff]blue central angle[/color][/b] that intercepts (cuts off) the [b][color=#0000ff]same arc[/color][/b]?
3.
Given your result for (2), how does the [b][color=#ff00ff]measure of the pink inscribed angle[/color][/b] compare with the [color=#0000ff][b]measure of the blue intercepted arc? [/b][/color]
4.
Try testing your informal conclusions for (responses to) (2) and (3) a few times by dragging the slider back to its starting position, [b][color=#ff00ff]changing the location of the pink inscribed angle[/color][/b], and [b][color=#0000ff]changing the size of the blue intercepted arc[/color][/b]. [br][br]Then slide the slider again. [br][b][br]Do your conclusions for (2) and (3) ALWAYS hold true? [/b]
Quick (Silent) Demo
Proof Exercise: Inscribed Angle Theorem (Case 1)
Case 1: Center of Circle Lies ON Inscribed Angle
[b][color=#0000ff][url=https://docs.google.com/document/d/14ZVo3KYR9NqVMFagPwZmucnSIdrqnM892AXSnvCAy8A/edit?usp=sharing]Link to Proof Activity[/url][/color][/b]
Distance in the Coordinate Plane (With Hints)
Discovery Lesson (Can be used without interactive figure below)
Parallelogram: Theorem 1
Interact with the applet below for a few minutes. [br]Then, answer the questions that follow. [br][br]Feel free to move the BIG WHITE POINTS anywhere you'd like! [br][color=#ff00ff]You can also adjust the size of the pink angle by using the slider. [/color]
1.
What special type of quadrilateral was formed in the first half of your sliding-the-slider? How do you know this?
2.
What else can you conclude about this special type of quadrilateral? Be specific!
3.
Write a 2-column, paragraph, or coordinate geometry proof of what you've informally observed here. (Hint: If you choose a 2-column or paragraph proof, this proof will involve a pair of congruent triangles!)
Quick Demo: 0:00 sec to 0:33 sec (BGM: Andy Hunter)
YOUR Linear Speed?
[b]Students:[/b][br][br]Use this applet to help you complete the [i][color=#0000ff]How Fast Are You Spinning?[/color] [/i]investigation given to you at the beginning of class. [br][br]Some key questions to consider are listed below the applet.
1.
According to NASA's website, what is the Earth's mean equatorial radius?
2.
According to your answer for (1), what would Earth's circumference be?
3.
What would the linear speed of a person who lives on the Equator be? (Round your answer to the nearest 10 miles per hour).
4.
What is YOUR current latitude? (For Southern Hemisphere users, use a negative number. For Northern Hemisphere users, use a positive number.) .
5.
Use your answer for (3) and your result for (4) to determine YOUR LINEAR SPEED in miles/hr. (Round to the nearest 10 miles per hour). For a hint, interact with the applet above.