IM Geo.3.9 Lesson: Conditions for Triangle Similarity
How could you justify each statement?
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAd0AAADZCAYAAABl2+rMAAAgAElEQVR4Ae1dC/gV0/o+pYRyL6USCaULJdGhUimXFBEhRQmpkBSK/FEukRLKtZwSIUlROnWUS4iQW0pUpyJKQhd3Wv/nXXxzZu/fzOy57j175v2eZ57Ze2bNurzfmvXOWutb3/qHohABIkAEiAARIAJ5QeAfeUmFiRABIkAEiAARIAKKpMtKQASIABEgAkQgTwiQdPMENJMhAkSACBABIkDSZR0gAkSACBABIpAnBEi6eQI6Scn069dP/eMf/zCOhg0bqpYtW6ru3bur//73v0kqKstCBIgAEQgVAZJuqHCmI7LjjjtOEy7O8ttMwv/617/SAQRLSQSIABHwiABJ1yNgDK6MHq4Zi++//17deOON+t4ee+zBHq8ZHP4mAkSACPyNAEmXVcETAu+//77Ry7V68PDDD9f3n3vuOavbvEYEiAARSDUCJN1Uq9974e+++25NqpjXtZILLrhA30evl0IEiAARIAKZCJB0M/HgvxwICKnazdvKHC97ujmA5G0iQARSiQBJN5Vq919oGT7GMHO24Brmc2FURSvmbHT4nwgQASKg6JGKlcAbAmKlnP3Uyy+/rLB0CPc5tJyNDv8TASJABP5CgD1d1gTXCIBYQaoHHHCAuummm/TRsWNHg2xxz26u13UiDEgEiAARSDACJN0EKzfsosmSIOntms+Y6+WQctiIMz4iQASShgBJN2kajbA8p512mu7pwoIZvV4cYliFaxQiQASIABFwRoCk64wP75oQ2H///UsYScm6XQw5U4gAESACRMAZAZKuMz68+zcC8DiF4WQQb7YIGVtZNGeH5X8iQASIQJoRIOmmWfseyo51tyBdDDFni2yAQCOqbGT4nwgQASKQiQBJNxMP/rNBQIyorJYDwYAKhIw1uhQiQASIABGwR4Cka48N75gQEE9TMJ6yEnGaQU9UVujwGhEgAkTgLwRIuqwJrhDYfffddW8Wc7tWIj6ZrYafrcLzGhEgAkQgjQiQdNOodR9lliVCdo+CjHOFsXuW14kAESACaUGApJsWTbOcRIAIEAEiUHAESLo+VYBe3ZVXXqlatmyph12xThUuESdMmOAzRj5GBIgAESACSUeApOtRwxhGBbmKC0SsUYWRkRgS4Xr37t09xsrgRIAIEAEikAYESLoetQwHEDAqgsFQtq9h9H7F4Mhuv1mPyUUa/O2331aTJk1SK1eujDQdRk4EiAARIAJ/IUDS9VETssnWHAXI1s6JhDlcIX/Pnj1bValSxeitI7+dO3dWa9euLWS2mDYRIAJEIPEIkHRDVjF6uyAxDDnHUdasWaNKly6dQbjIL47mzZvHMcvMExEgAkQgMQiQdENWZdxJd9CgQZaEK8Q7b968kBFhdESACBABIiAIkHQFiZDOTu4SQ0oiUDRmgy8hWvN5yJAhgeLnw0SACBABImCPAEnXHhvPd2DZDP/DIDGneV/PEYf0AHrhlSpVcuzpjhgxIqTUGA0RIAJEgAhkI0DSzUYkwH/Z0N1qU4AA0QZ+dNy4capp06aOZCu93WXLlgVOjxEQASJABIiANQIkXWtcPF+VYeW4GFBhGdDgwYNL9Gy7du2qatWqZUnAl112medy8wEiQASIABFwjwBJ1z1WtiFlmRDmS+02BLB9OOQbc+fO1ct/pOeKc7Vq1RQ+Cr744gud2tatW9XVV1+typYtq8l3xx13VPfff3/IOWF0RIAIEAEikI0ASTcbEY//40C4v//+u3rggQdU48aNM3qwLVq0UI899phtiZ566ikd/uijj7YNwxtEgAgQASIQHgIk3QBYFppwP/30UzVw4EC15557ZpBtjx491BtvvJGzZC+99JJ+DsPNFCJABIgAEYgeAZKuT4wLSbizZs1SZ5xxRgbRwgf0LbfcotavX++6RB988IGOA64rKUSACBABIhA9AiRdHxgXgnB/+ukndd9992VsrID52tatW6vJkyf7KIVS69atM4j7119/9RUHHyICRIAIEAH3CJB03WOlQwrhYj3u9OnT1SuvvGJ7hLFWd8mSJXoLwQoVKhgEWapUKXXxxRcrbFgQREC0YnD15ZdfBomKzxIBIkAEiIALBEi6LkAyB8GSICGqXOcg63VnzJihOnTokJFWjRo11PDhw9W3335rzlKg37IrEoaaKUSACBABIhAtAiRdj/iipwsydXPAA5QX2bJlixo1apSqW7duBtmeeOKJ6qKLLlLXX3+9l+hchT3ooIN0WjCqohABIkAEiEC0CJB0o8XXVezYo7dv376qXLlyBtli7WyfPn3U4sWLdRyY04VXqY8//thVnG4DiacqLB+iEAEiQASIQLQIkHSjxdcx9qlTp6qTTjrJIFoMVx966KFq5MiRavPmzSWexYbz6PGGKe3bt9fpw0iLQgSIABEgAtEiQNKNFt8SsW/atEndcccd6uCDD84gW5AfDLNySffu3RWGuMMSxAeyDzL/HFZeGA8RIAJEIOkIkHTzpOFFixapXr16ZWwgX758edWvXz9PQ8YrVqzQy4beeuutUHIO5xogXQxvU4gAESACRCBaBEi60eKrMFfapk2bjF5tgwYN1D333KMwT+tHXnzxRdW8eXO1atUqy8fhf/mXX36xvJd9EdbQIN2zzz47+xb/EwEiQASIQMgIkHRDBhTRbdiwQd16662qZs2aGWTbsWNHNXPmzFBSnDhxojr55JPV6tWrS8SH6/PmzStx3erC+PHjdR7hZINCBIgAESAC0SJA0g0R3zfffFNdeOGFGUSLdbADBgxQUexTi7ndVq1aKVg/i6AHjR2E3ArWA6One9hhh7l9hOGIABEgAkTAJwIkXZ/AmR+DVXG204wjjjhCb5f322+/mYOG/hvGV7Vr11ZTpkxRy5cvVxi6/uqrr1yng40RQLpVq1Z1/QwDEgEiQASIgD8ESLr+cFNwm3jTTTep6tWrZ/RszzrrLDVnzhyfsfp77KOPPlKdOnXSBlajR4/2FAmIGqSLdcEUIkAEiAARiBYBkq5HfF999VXVrVu3DKKtWLGiGjRokIJlcaEEPd5GjRrpYWLsreu2h40lTCBdHD/88EOhss90iQARIAKpQICk61LNjz76qDrmmGMMggJJYfP3Rx55xGUM0QWDpTKGtxcuXKiJ/5prrlFHHXWUdim5cuXKnAmXKVNGl+vzzz/PGZYBiAARIAJEwD8CJF0H7LBL0JAhQ1TlypUzyLZLly5q/vz5Dk/m99btt99ewrkFet1YDtSsWTPVuXNnvURpwYIFauPGjSUyV6VKFV0+kDaFCBABIkAEokOApGuBLZbbnHvuuRlEu++++6obbrhBrVmzxuKJwl2C5TJ63E5DwyDTu+++W11wwQXaf3Pjxo21+0nMA2MOerfddtNlfeGFFwpXEKZMBIgAEUgBAiTdv5W8fft29fDDD+thWZnjxPnYY48N1e1iFHXK62YF8OuMYWdsnoAt/UDaKGuY7iWjKCfjJAJEgAgUOwKpJ13MY1577bVq7733zujZnn/++eq1114rdv26yj96uyDdO++801V4BiICRIAIEAF/CKSWdP/973+rM888M4No99tvP3XzzTerdevW+UOzSJ/q3bu3xgEGWBQiQASIABGIDoFUke6vv/6qxo4dq5fWmIeQW7ZsqR5//PHoUI55zJirBh7wpkUhAkSACBCB6BAIjXRh6fvKK6+oCRMm6PP3338fXa49xrx06VJ11VVXGQZDQrg9e/bUy2w8Rpe44HAdCUxOPfXUxJWNBSICRIAIxAmBwKT78ssvK/QUhcjMZ+zVWkjyhTXuaaedlpG3Aw88UN12223qm2++iZMeCpqXyZMna4ywDplCBIgAESAC0SEQiHSxBEVIFs4ZsBE6DuwRC0f/uNewYcO8Eu+2bdsUXCHWr1/fyBvyAV/ITz/9dHRIFnHM2AoQGB188MFFXApmnQgQASIQfwR8k64QLsgVvd1sQQ/38MMP1405wkYt8D98+eWXq5133tkgW3hauvTSS7VVLu5RrBFYvHixxmzPPfe0DsCrRIAIEAEiEAoCvkgXJIueEQjXvK1cdo4kHMJizjcKee6559Qpp5xiEC3Swq47I0aMMHrYW7ZsUfXq1XPtjziKfMY5zrVr1xr4/f7773HOKvNGBIgAEShqBHyR7v77768baTfOFKS3C3IMS+B96a677lJ16tQxyAJki83bn332Wctk0rTu1hIAh4s//fSTgePXX3/tEJK3iAARIAJEIAgCnkkX5AmCA/G6EdlnFnO9QeW9995TWFNatmxZgyR22mknddlll2nPSk7xww3ivffe6xQk1fd23XVXjSm8VFGIABEgAkQgGgQ8k67M5bolUbEedgqPpUZdu3ZV1apV0wZPDz74YEZpsUH7CSecYBAtSB/DxSDSrVu3ZoS1+wNnGH379rW7nfrrNWvW1PjGaSOH1CuFABABIpA4BDyTrlglWxlPWaGTq6eLYWKQaPaB3XGwe06tWrUy7mEt6fPPP2+VlOO1Tz/9VHXo0MExTJpvNmnSROOMDxwKESACRIAIRIOAZ9IVcnSbHSFdq/lfzM1KfE5nDH32799fffLJJ26TLREOm7U3bdq0xHVe+AsBzIdDB/fffz8hIQJEgAgQgYgQ8ES6sEAWcnSbHwlv1TPGxvBy3+q8yy67qDFjxihs0h5U4AKyQYMGQaNJ7PMwNIMOhg4dmtgysmBEgAgQgUIj4Il0zUuA3GRcwmNI2krE568V4eLaAQccYPWYr2tYCoN5YIo1AnCTCcy5ntkaH14lAkSACISBQKSkK0ZXds4xYNxkR7i43qNHjzDKqOOApyp4paJYIwDXmMD83HPPtQ7Aq0SACBABIhAYAU+ki9SEJJ2cYiCceSjaamhZcl63bl0jTolbzmG6bfziiy9U69atJVmesxB4+OGHtR7atm2bdYd/iQARIAJEICwEPJOuGEbZ9V6RMbiAhM9lkCeWDDnJm2++qQ499FBL4m3cuLGCNyk/MnPmTIUN6kXeeustvSxJ/vOcicC0adO0Dho1apR5g/+IABEgAkQgNAQ8k67M04JQrSyS0cMVwoU3Kre7DM2ePVsNGTJEwbhq0aJFqnLlypoE2rVr56uwAwcOVG3atNEWy/C/jL1icfz888++4kv6QwsWLNB4V69ePelFZfmIABEgAgVDwDPpIqdwdCFDwCDYm266SV155ZUZW/x5IVyr0sNhhqQRZG53/fr1CnPHrVq1Uti6Dr3qTp06qWHDhils/Uf5C4Fly5ZpvOHhi0IEiAARIALRIOCLdJEVuIMUv8pCjjjDPaST9ykvxcCcrsQ9aNAgL4+WCAuPVsuXL1d//PGHevfdd9X48eP1xvYlAqb0wsaNGw2s/Q7ppxQ6FpsIEAEi4BoB36QrKWA4GUPOcMkIgsQyH7dDyhKH0xn+koV4kYYfgTcqDDVTnBEoVaqUxnrVqlXOAXmXCBABIkAEfCEQmHTNqYqf5Y4dO5ovB/59/fXXG8Q7efJkz/GBuOFSkuKMwD777KNxxpw6hQgQASJABMJHIFTSRQ9Xtv0La4hZinzRRRcZxDtv3jy57OqMXi42uac4IyDLt2bNmuUckHeJABEgAkTAFwKhki5yYLZudlqf6ye37du318RbqVIltWTJEldRzJgxQ3Xv3t1V2LQHatGihcZ34sSJaYeC5ScCRIAIRIJA6KQbSS7/jhSbrctuOPXr11cw/sklGOrmdnW5UPrr/hlnnKFJd+TIke4eYCgiQASIABHwhEBRkS5KBiOfGjVqaHI4/vjjHQs7YcIE1atXL8cwvPk/BC655BKN6+DBg/93kb+IABEgAkQgNASKjnRR8oULF6py5cppgujSpYslGCBn9Iax/pTiDgExWMP8OYUIRIUAlhu2bNlSu4qNKg3GSwTiikBRki7AnD59uiZdLCfCXrvZAjeVWItLcY+ALPsK2/rcfQ4YshgRgAElnNlkH3ZLB2WVQy7/7cWIBfNMBHIhULSki4I99NBDBvGalwTBQxbcQFK8ITBp0iSNZ7Nmzbw9yNCpRsDsoU7W1MsZRoxYy28W3INjHQoRSCMCRU26UBg2XZcXHH6bR40apbp165ZGXQYuM/xfA8s6deoEjosRpAcB6blidAkEjKNfv37G8kGzwxwMLaOOWfltTw9iLGmaESh60oXy+vbtaxAvlr1s3rw5zTr1XfZ33nlH41ixYkXfcfDB9CEga/Ozh5PxX1zFijc5kPHuu++ePpBYYiLwNwKJIF2U5cwzz9SEUaFCBe1bmRr2jsDq1auNj5ft27d7j4BPpA4B2TcbxGslMvQMsoWE6ZvdKr24XsP8NYzHBAe7fAJPhHPaOtXuWV4vDgQSQ7p//vmnat68uSaNgw46SGHTeoo3BLZt22aQ7oYNG7w9zNCpRECGizHEbCVm0gXxYGg5e47X6rmkXRMjxVykK3iSdJNWA/5XnsSQLor01VdfqUMOOUS/2Mcee6z67bff/ldS/nKFwC677KLx++STT1yFZ6B0IyCkirOVyHwvSAdHWskE5XYzlw1SRjgZjrfClNeKG4FEkS5Uga9pzBmh4sLDEsUbAuJ45NVXX/X2IEOnEoHjjjtOv2tWLl/FJSzeR8zvgniswqUBOJnbztXLd8IzDTiloYyJI10oDZvWg3Rx9O7dOw16DK2MjRs31rhNnTo1tDgZUXIRkPdMSghyxXpdLBWSe2m3VAYmwMKNAZlgJnjynDwEEkm6UBOc9ksFxrpdijsETjzxRI3bgw8+6O4BhkotAjJHK+9Z9hm9trT2bM2VQnr8wMNJBE+uYXZCqfjvJZZ0oZo777zTIN4HHnig+LWVhxKcd955GrNbbrklD6kxCa8IoNcIcsvVgHuN1094yQsskpEfHLJ8KJfBkJ/0ivWZXPPeUi63xlYSnufiRCDRpAuVDBgwwCDeadOmFaeW8phrMeS48sor85gqk8qFAIYozUO2cSBdqStmox/prTVs2DBXkVJzX4zJYJnsJG6NrZzi4L34I5B40oUKunbtqom3bNmy6o033oi/VgqYw2HDhmmsgBklHgjA+AYkhh6uNMxxIF0xDgLRmkV6u9nXzWHS9FsMO/Hh5CR2eDo9w3vFh0AqSBdqadu2rW60qlevrlasWFF8mspTjjGXi8Ydc7uUwiOAhloabTFIisvwMvKBI1ukB8whZqXXJAMjfIg4iRdjK6d4eC/+CJR8Y+KfZ185/O6779Rhhx2mGwlY6G7dutVXPEl/CFbLaCSAESUeCGBO0GyQBP0UuqfrZBwkQ8zwuZx2EWcXds5DBB8nPCUMz8lAIDWkC3Vhb93KlStrUmnXrl0yNBhyKbDcw82XecjJMjoPCMSBdHMZ/chQaa55TA/FLsqgbo2o3IYrShCY6QwEUkW6KLmQChquHj16ZIDBP0otWbJEk2758uUJR0wRiAPpytyyDHlnQyWkjHBpFhlqt8NJsJGPFPOIhtyLwxmjF1h6mascTnnFhwXisDviWnanMvm5lzrSBUhPPfWUJhY0XoMGDfKDW2KfWb9+vYHNjz/+6LmcMPoxb2aey3jEcwJ8QOun0MPLIFPkwc7DEq7jfqHzWejqIqQLwrETYIW2yI3zDLs4orwOot1jjz0C1zuU0elwwijK8uU77lSSLkC+5557jApgXvKQbwXELT1sHCEvBnYdciMgVny9Yg5PnjWfsdSF5OsGSXdhgG3aycwdUoUPJT1+7BxkJXgvxDI9jqQjIxrSEw9S71BvEQ96tFaH3QecFW7FfC21pAulXXfddQZJTJ48uZj1GGre9957b43Lu+++6ypeeSFhoYkve3wZYy4PjYhY3nLdpisoXQUi6bqCKRaBQKryDoB4p0+frgkHo0ETJkwwPlTxDsVJQIDyMQAjMDGO80u6QZ+PEzZB85Jq0gV4PXv2NIh33rx5QfFMxPO1a9fWmMCHtRvBV6vdaIG50Um7UY0bLN2EIem6QSk+YfB+CPFCd9kHSC1uI0Hy3krvG2UIUu/keYkvPtrJf05ST7qAvH379rpCVapUSRsS5V8N8UoR2yLiBXv88cdDyZibea1QEkpJJEEav5RAFLtigsQwAgTSQW8R7wQ+VOM8pGr+EBDS9NvTledJukqRdJVSMBhq0qSJJpr69eurjRs3xu6lzWeGOnbsqLGw6716zQtJ1ytizuGjIN23335b9e3bVx1xxBHqkksuUdza0VkHabsrpOmXdPHBgXpL0iXpGu/OqlWrlOwle/zxxxvX0/jjoosu0i/I9ddfH7j4+FoWAyvM61CCIxA26aIhRJzZR//+/YNnljEkAoGgpCt1DPPEmNuGNTQO/Iaf9zj3+MNWIHu6JkQXLlyoypUrpxufLl26mO6k6yeWUaEB7tWrV6CC40WSXnMujzyBEkrZw2GS7qefflqCbM3kix4whQgEJV3Yc2BeGwd6yzjEABP1DQSM3nAahKSbpWVYF0qjk9Yv/bvuuktj0KlTpyx0nP/ipcGXqxzAERbNHFJyxs3rXeDqd5gvO62bb77ZqO9S781n7jaVjVg6/wclXTvUMBImvWDUuzT0eEm6FrXhoYceMhqi4cOHW4RI9iUsZcAL0KJFC08FNb880nCDgEePHh0760xPBYtZYGAbFumeeuqpRl0XnZnPrVq1ilnpmR0498EwbYUKFVSDBg3Uo48+GjkoUZGuZBwjYah3sP9IupB0bTQ8dOhQozFKy7CHQDFr1ixd9rp168olz2e8pBhSkpcJ87pp+Ir1DJSPB4Bt0PnxxYsXqz59+qgddtjBqOdmspXfYczr+ygiH7FBoHfv3pb6Ouecc2yeCOdy1KSLtgJ1LqyPyXBKHU0sJF0HXGHNKY0PiCgtgnk8lHufffYJpcji1YbzuqHAGSiSZ555Rm/bKPU613n58uWB0uPD4SHwzjvvGO2Rld7crqv3k6OoSTfq+P2UOapnSLo5kD3zzDN1Rd91112VWw9NOaKM/e2VK1fqMpcuXTqUvKKHK41EKBEyEk8IfPvttwrTJAcddJChB+gD69PRw5A9lEVHch45cqSndBg4WgQGDx6coT/Rk5wvvvjiyDIQNSnKkqI0fJiTdHNUU/gibt68ua7saLS++OKLHE8U/+3NmzcbLzca7DBEGoYw4mIc7hBYtGiRXnOLjyfBH7tHXXHFFeqjjz7KiAR6HjBggA6HMOvWrcu4zz+FRwArKkSPVueaNWsq9IajELekiw1T/KzxFkvmNEzlkXRd1NCvvvpKHXLIIbrCw1vTb7/95uKp4g6y00476fJiSUlQkRcWlsyU6BF48sknFdaamxtmGNxgkw+nnaOwVl2e2b59e/QZZQqeEDAbeIqerM6wxcBcfJgjc/IO55pzrVixoq5DQ4YMySgbnoOBptnLFQIgXhhbohxx8z+dUYAQ/5B0XYIJwxXxn3rGGWe4fKp4g1WvXl2/CAsWLHAsBIaOnYx68JKJ4/Q0WCY6ghXhTfQwbrnlFsMRiTTGWCc9c+ZMVylv3brVIN1vvvnG1TMMlD8Efv/9dyWbkYh+5VyqVCnVpk0bQ39yvV69egoEGJSA3ZDumjVrjPRR78wi+bE7g5SzCdn8fJJ+k3Q9aBOGClJpYEWYZBGixJyfk8jLCOtkrOnEFn/4osUZ/2UfTnzFpuWlcsIr7HtvvPGG6tGjh1EvUT/xcYih4mXLlnlObuedd9ZxffLJJ56f5QPRIzB79mxVtWrVDH3D3mTKlCk6cUwTPPLII6pdu3YZYVAvhIDfe+89zxnFxzWWBOYa/u3cubP27IfRFrPgebiVxZwtCFYOfIijDUmTkHQ9anvixIlGZQaxJFXkqxkvsJPgZYJ1sowCyEeJnMU5RhIIN06Nw2OPPabXUQvOOMNvMuwO/DSqouP99ttP128/83ISB8/RI3D22WdrPZ1wwgm2icGH/MMPP6xOPvlko82S+gIf8zfccIPC0jFKfhEg6frA+8477zQq8QMPPOAjhvg/gnV/eEFvu+0215nFMDOISQ4QclJErCvD2gTCDy4w4kNvo1q1akb9g47OOussNWfOHB0lyPjSSy/1E71+BsSNOJ999lnfcfDB6BHAnC30hM0p3AimCzAnfNJJJ2XUHcSB+f7/+7//c5wmcpMGw7hDgKTrDqcSocTSE5V22rRpJe4X+4XLL79cv5xXXXVVsRelRP7xMdC9e3fDgAM6lOFxux65rDUuRG8XG5537do1o7GEwQp8ZH/++eclynfuueeq7OG9EoFsLqDnBDzQQFPii4BX0jWXZMOGDXqZ2FFHHZVRp6D3ww47TH/YOdlpmOPib+8IkHS9Y2Y8IQ1h2bJlFebWkiTik/f8889PUrG0mzk0LnLI3JL8xxy0VYOD4fN8W1fCvd8///lPI6/I49FHH63n7Jysi5csWaLq1KljOXQIJy/XXXedrU5lWQqMsijxRSAI6UqpMJ+KkTqs0z7xxBMz6hnqmhDwBx98II/wHAICJN2AILZt21ZXVlj7rlixImBs8Xl87NixulwwyEiKSG8VBJptEIIerrisBPGae7zo3aIRyn4mClzQC0eDCm9g8iGAM8hw3rx5rpPExh34oDD3hP/44w9t4fraa6/ZxoM1vEiPGx3YQhSLG0FJ9+OPP1ZY/gg/BCKwgAcJy2iHuf7hgxM2LB9++KEE59knAiRdn8DJY5s2bdJfhKigjRs3Vlh2kQR5+umndePbpEmTJBRHD5lBRyBcM6FmFw6GXwiHuVMR9AjwXJTy0ksvKZlHl8YOy0Ow3GP16tW+kn7iiSe0sZUYVmH3KDTWTiI+xzGKQ4kvAkFJF/P+MAq1k6+//lrdf//9SjoVUidxxsoGjIRlO1ixi4vXMxEg6Wbi4evf0qVLVeXKlXVjnZSe4fz583V54OWm2AW9R1m6ZDV0bC6fGEyhYRHBV76ZhOV60DN6GZg7xYeNuVFDDwR7GV9zzTVBk1DPP/+8OvTQQxWM//BRCFUrJ1YAABwuSURBVItWJ0FPB3mBwQ0lvgi4IV2MbFjJ448/rs477zyrW5bX4BwII1+yosFcVxs1aqTwoUYCtoTO8iJJ1xIW7xdlCBIVEusmi13wEqEsWANY7CLDyjjnErMeERaEDRycesdWcf70009Wl/W1zz77TBPqXnvtlUG2mD+XoV/0NDB/G4bgo7BWrVqqdevWCsOKToINEVBeEDQlvgjkIl18JFp9KC5cuFBbK/v1NOeGgHPVsfiimp+ckXRDxBn7XKLBwgHL0mIWvFxSlp9//rmYi6JkyDhXL1cKKeXGfywRckPWCAs3iljCseOOO2rsMM9vXnoDxwadOnUycEU6WBeLoTorX8cYNfHj4ELKIWc4TsBwMYYT0Yvu37+/ev311+V2xlk+OuiyMwOW2P3JRbro5WJDixkzZhh5h0EULJbD2o0IdXbMmDElXI6iXmPp2bBhwxSM+iiZCJB0M/EI/A/+baXRLuSazqAFgX9pKUcxb/IAokU53M7Jokcr5QaGeB693Vyydu1aWwch2KlKPHxJ3PA3i2E+J8FyLQwPBxHYGBxzzDGGG0A0xpMmTdJre7GRx9VXX63JGMuSMLrxwgsv6PJj0wNKfBHIRbrIObboPPLII9WXX36p186DCGFgF4Ugjfvuu0+PpkgdlzNGTWANTy9nfyFP0o2gBmJJhlS4yZMnR5BCfqJ0Ow+an9z4SwVDbNAFLHndiPT08IwXueyyywydi+6tzj179lQY4nMjMHwKul4Wvehbb73VMjkYaE2dOlXPyWFbOHwcmJ0nOG2OYBkhL+YNATeki8zAGAofV02bNs2bu0V8pN97772qVatWJd4JfASgPqaZgL21LHmrUsWfEBpXaXS9LPWIU8kPPvhgXYa5c+fGKVue8iKkazW/ZRURfE1Db17X5MoHiug8+4whajgl8CJw4Qfi9Svbtm3T3qm8kCd6wpJ3OLCnxBMBN6QL+wC4ixRDukKUBCNAuQgYNgdpEpJuhNrGnAoasEqVKhXl3IY4Zijm3roYUbklXSwPgs7czuNK9ZF5XCGs7HOuoWSJx3yG3+sRI0aYL+Xltxh4Bd2ZJi+ZTWkidqSLDy14yOvWrZue08X0BD6eYGUsS8cKBRkIGNNvspWf+R2BBT9czoZhwxBF+TDNhCkYHEGFpBsUQYfn0cOQ5SBwMJ5ruYZDVAW51aFDB01A+FItVvFKumJ05dURhjjWMDck5t+Y8/Iqo0eP1sODXp8LGl72jg7L4CZofpL4PBpxuB5FHfEjQrqYDoC/bcyZwoEKerV9+/YtYSwFIs7ebs9PumE9gw8B1G9M+5jfE/yGsdftt99ecAKGfYd5pzRzPmGjkWsHNjus/GncLjZeL4EALFpr1KihKxY2Fi8mkS3j4Ay9WEWGl93M6coa3VwONKywwBC8+aU0/waJ5RIsMcJQIL72X3zxRQXrcVjAY8413wILZ+TfT+8833ktxvRQz8zTEX7KIKQLV42wEkacb775pvr1119to8MzCBs3gW0BjE5btGhR4h3CsjkQsN8lTn7LCsIV40e0B/ioRluCj3j5MHc7epadB5JuNiIR/IfhTLly5XSFwtdosQicM6DxLea9g2WOFo2c01pb3JOeh9+Xady4cSUaDSHfXI4u0FjC2hSGU8AbFsdwBYmlPujJ5NP9nvTa0ROhhIuAjLzAZgAH6ocfEdJ1u8sQ0kAdc3oH/OQj7GewUmDUqFG2BDx8+HC1fPnysJMtEZ9MM0FHVqsXYHDpF0t/Gi+RRV7IhQBM9aUBxjrJYhDZwhBbxxWzyJcpdhayErw88lXr1YDKKj64dMSabTi4wDIK0fvIkSOtgltew9po7I2LNbYYaQARYgs2WKNGLWIEiIadEh4CMpQKXaLOyX8/KfghXT/pFPIZIWBYX8s7JGdYY99xxx0KjmaiEPRukZbfIWSnPJF0ndAJ+R56MVJp8MUWd8EuN8gvTP+LWczLgGDEgQ8gMYqAE3cZ6gPh+v16dcIH/pNF726HbP/zn/+oCy+8MCPaLVu2KOyLGrVce+21Or9wRUkJDwEMAZtHUUi67rHFNB0+Wps1a2a8S/JOweATHQQ7Asb7jiVxcH3p1ihU4o6iPSDputd7KCHFoTyUipcwzgLLR+QTPaxiF3yxSo9XXijzGcNJUbxgghteekkPhJpLsF8zNiwohGCZEvIK71mU6BAg6frDduXKlXopndgeyHuFM6ZlQMDYXQsOfmBHY76P37DkhiW1k8gz+GAPW0i6YSPqIj5YF4pSYTQTV4FhBvJZpUqVuGbRU75AqiBfMYiQIaR8ffyINTiW5Dg5iIcRFT50CrVj1YQJE7TeQQqU6BAg6QbHFtupYlkdyFbaVDlXq1atxDW5l2sXLZl7x7ST1ZxukJyTdIOgF+BZeP9BBcCGAnFdD4mvReSxTJkyAUoa30fdGlmFVQLM02I5BDDF0g47Zxnw2IP5qkLJzJkzdR7r1q1bqCykIl2SbrhqRntlR8BCtubzt99+a5sBfKCLoRumn8I0KiTp2sIe7Q1s6yYGAjCYiaN/Y1Q8qaTfffddtIAUKHax1MVcbz4EX80yzG2VJpzSY213lEPducr51ltvab3DepoSHQIk3eiwxdyttF125zlz5jhmAO+gtA+IA+9rGL1ekq4j7NHexDCiOCLA/ATmIOImZcuW1ZXXzkghbvn1mh+8WEKCmNfNh4DUdtppJ40r1uaapXPnzurpp582X8r7bwzZoZEpXbp03tNOU4Ik3XC1vX79eoX9oE844YSchIv6bTfSlJ0rjIjJVBR6vXBsEkRIukHQC+FZKFAUesYZZ4QQY7hR7LvvvroCY343qQIdYJ4XR756mNhyTb7Ar7jiCg3t4MGDVRyW6WzevNnIm9MQXK76AFxhJe4XU/QqxMrc7pwrD3G+T9INrh0Q54MPPqhOPPFEo87Ke1WxYsUS1+QePm69COqwDDdbjVB5iYuk6wWtiMLC3Z5Uhrg5ooDHG+TNvC9nRDCkLlpsaCB6b9u2rV7WEBcQxJmLX09A+ICRsvm1ADXHIXFln+OCl598kHT9oKZ0DxVEa94RS+oFDBCxrh0ffDBEFP/xch/n2rVr2y4vcsqReemhU7hc90i6uRDK032xGEWlwNrRuEjr1q114zl+/Pi4ZClR+YBbPmkQgm7jFyYwYvm5YMECT9GiR4CegJQJZ7+kKxakOMtIRPbZU+ZiFpik614hWJ+O98OKaOHX/oYbblCLFy+2jBBr4zGKeOqppyp86PoV1G2p137jwHMk3SDohfwsLFZFqZibiINgGAZ5KqQ1bRxwiDIP5r14sYl8HESG0jCf5VbQuxBHIyBHIRW/pCvP+x2edpvvQoWT8vlJPw0eqbBBDEjy5JNPNtpFaR9BtHA6k8+dk2S1A6YDgwhJNwh6ETx71VVXGRUMO4MUWvr06aPzc/XVVxc6K4lOH6420aCUL19eLVq0qOBlbdOmjc4Pthd0KyBqNEiy7llIJSjpuk2/2MIJPn7y7Zd0sbFGnAU2BKhz7dq1M9pBIdp69eppoo1qiSU+7uysk3FdfLNj5CWIkHSDoBfRs3BXhooGy+E33ngjolTcRYv5EeTFzm+xu1gYKhcC27dvN5y8H3jggXoP1FzPRHn/nHPO0XrHrkduBY0WersiQip+SVd62xJf0s6Cj59yCek2btxY79DzzDPPODpcQRrYyxajKnETEC02CznllFNKEC3WiqOsURGtGQvUU7R12AIRU3xYm4uzeXs/1MmgIy8kXTPqMfotPY3q1asrLOEolIjD/vbt2xcqC6lJFxskwMgDLz4MQH755ZeClV2GvDHy4leEVPySLnBAI5dUEXz8lE9IF24OsQkGLN+xphRrvLGj1WuvvZYRLebm4bUpH767MxK2+bNp0yZbooXjmOuuu0698847Nk9HcxkfjLJ8EHUv+0APNyjhIuck3Wj0FzhWVEpY4kHx+JotlEvAJ598UucBu3pQokcAzjFkXrSQm47jCx917/zzz/ddaCGVIKQLN3zIi/mA0WEYjZ/vgoX0IBp5v9gI6WZv7Ye1qpMmTdJ+s7EGHDte/fjjjwrW8VglUUiBgx0YZOIDPpvQQLT4cIjD1IroBXv8Qj9+dWSHNUnXDpkYXF+6dKneUxUVFHMchRA450f68JpFyQ8C8JQjjVKhdvoZO3aszkOQehcG6QoO2Wd8mMjccX60Eq9U7EjXnMvZs2cr+PuG61FY9xZC8HGE3crE77hZj3Xq1FGDBg3S+0gXIm+FSpOkWyjkXaaLryypqD169HD5VHjB8NWH9INa7IWXo3TEhI3rRe+YV8+3wCsW0keD7VeCki6MV1D/xbgFDTj+y1Ii5M+LdbXfcsTxOTeki3xDjxiix/ac8ISWD/nhhx/0BxGW6EgdljOmT9JItGbcSbpmNGL6GxuiS6VFhc2nwCe0pB1HN5X5xCLfacF5u2CPnmc+Zd68eTrtmjVr+k42KOk6JYyhP2ADi9I0ihvSxQYAsPjFjlbYzQxDuFENMQvRmn0VS92Fq1vs0Zwv0o97fSDpxl1Df+cPlodSidHg5EtgzCPprlu3Ll/JMp2/ERg4cKCB/9SpU/OGy4cffqjTxS5YfiVK0kWepF5iNCZt4oZ0u3XrpjD/LbJw4UIFD3NwqRmGwF0o4rci2oMPPlgbdCFNSiYCJN1MPGL9DxZ90tBgF418yW677abTRUNMyT8CaDyh9x122EF59RDlN7fYjEPqGrYk9CNRk27U8fspc76eyUW6+DAXn97mPGF4HhbOMmRvvufm95YtW9TEiRP1shqpH3IG0WI9f5L9tLvBKFcYkm4uhGJ2v2fPnkZjiCHAfAjWjeLFyld6+ShTsaUhO6dUrVrVl99Yr+XFVII0pn63nYyaFGWjEPZ0rbVrt1kFLIgvvPBC64csrmLlBGwMTj/9dKNOSN2AgSWIttD+BCyyHdtLJN3YqsY+Y2JyX6lSJbVkyRL7gCHdkY3XC73lXEjFKcpoYEQkziIaNWqkMLQXtcjSJb+kFiXpioEf1lWmUXL1dHNhAtLFckA7AdFi6RF8FpcqVSqDbGvVqqUw7UGitUPP+TpJ1xmfWN7FujsMEeFrEz5I4aM0ShFPMWPGjIkyGcadAwHs+FOlShWtdzh+j1rQi0Edmzt3rq+k3JAufIxXqFBBeyMyJwKrZAyFWgmui0u+fNo3WOWlUNeCki58FmdvUbdt2zZjjS/2UpbeLM4Y7RowYIB6/fXXC1XkxKRL0i1SVa5atUrVqFFDvxjwShOlyBINOCigFBaBV1991eh5BPUBm6sksi2aX/sBN6RrXlayevVqI0uyrR/IFeQAV3xwFgJnGUIGUZffyEwMfwQlXRSpb9++etgYu/B06tRJZRMtLNfhkSxfdgQxhDmSLJF0I4E1P5HCMlD2Pe3SpUtkieILFw1dHP22RlboGEc8ZcoUg3jg8i8qEYcG9957r68k+vXrp3cachqeFs9X2c5XYOgDUs12y4d5XFjL2vWCfWW0CB8KQrrY9OCJJ57QuskeOgbR9u/fv4QbySKEKLZZJunGVjXuMjZ9+nSjAcbLEoXcfvvtOg04wafEAwEQofT4Ro4cGUmm4IwFaUTtnAOuL//8889IypDUSL2SLizQMWKB3azKlClj1B3oF6MJJNr81RSSbv6wjiwlbO4sDfDw4cNDTwdbbSH+qIexQ894wiOUhhe6wRBh2AKrVMTdu3fvsKNmfAERkGVksLewEyFa7ImNHcukjcAZIwgYssd0BSW/CJB084t3ZKkNHTrUeKnC9kkrvekk7/gSmWIijviiiy4y9A4/2WHKHXfcoeNG74gSDwRAkmLgJiRauXJlNWvWLJ1BOLOBVTKIdscddzTqBsLCBgRD/mE5x4gHIsWXC5Ju8enMNscwjJAXEW7fwhJYLCLeatWqhRUl4wkRATFG2muvvXLuqeolWTiqh97ht5cSDwTwDso7bj7DtgPraK2IFk4y0j4HHg/t/ZULkm6ctBFCXs4880z9UsJ9H5YFhCFYqoIXHC82JX4IwDDm6KOP1jqCf90NGzaEksnnn39ex4llaZTCIwCnFmaitfu93377aW9UJNrC68wqByRdK1SK+BoMUpo3b65fTgxD+fUmZIYAnm3kBc+HUwZz2vztDgFY+8ra1ez1l+5iKBkK7vygd6wNphQega5duxrvobyP5jOGj+fPn1/4jDIHjgiQdB3hKc6b2JgAO3vghTz22GNVGLsDwe8v4lu5cmVxgpKCXGMXl5133lnrCRuYB5XPPvtMxwVrV0rhERDDNjPRmn8XYuvPwqNSfDkg6RafzlzlePHixXoPXLyUcOUWVGCsgbi4PVdQJKN9fsaMGVpP0JWVw3svqcP1pDTq3333nZdHGTYCBOB2UfRhdX7hhRciSJVRho0ASTdsRGMU3+zZs42XNOiyD+zLiRd95syZMSohs2KFwMMPP2zo/dZbb7UK4vqaLDVBr5dSeARk7XQ26cJbF6U4ECDpFoeefOcS+13KCxrEjaO49DPvz+k7U3wwcgSGDRtm6H3cuHG+09t33311PNyuzTeEoT8IfWLTAbzXmMe/7777Qk+DEUaHAEk3OmxjE7Ost8RLCgfzfgS+WfH8iBEj/DzOZwqAANx2ygeX36HHBg0a6DgwbE2JFwJ//PFHvDLE3LhCgKTrCqbiDwTH5dIAT5s2zXOBLr30Uv38tdde6/lZPlA4BODYAnovX768WrRokeeMtG7dWj+P5SoUIkAEgiNA0g2OYdHEcN555+kGFPN0XvfCHDJkiH62Z8+eRVNeZlSp7du3qxYtWmjdYXu2NWvWeIIFno1A2hgtoRABIhAcAZJucAyLKoY2bdroRrR69epqxYoVrvM+evRo/Rx2eKEUFwJff/21ql27ttYftuuDq0C30qdPH/0clqtQiAARCI4ASTc4hkUVw6ZNm5TM0zVu3Fht3brVVf7hUB89nmOOOcZVeAaKFwLYyWfPPffUOvRi6YodhqD37t27x6tARZgb+ESHMaOb4+677y7CEjLLbhAg6bpBKWFhli5dqvbZZx/dmLZr185V6ebMmaPDw+kGpTgREB2CRHv16uWqELCMRfj27du7Cs9A9ghgwxBg6ebAagFKMhEg6SZTrzlLBb+s8vK78WQDP84ID6f6lOJF4LHHHjP07mafXOxYA703bdq0eAsdk5zjnTMf6M0CW5Cx+Tp+w60nJZkIkHSTqVdXpXrqqaeMBnjQoEGOz8AAR0iaSxUcoYr9TSz7El2OHTvWMb/YLhBhsS6UEi4CN954o8YWZ0p6ECDppkfXliW95557jAbYaR7pxx9/NMKtX7/eMi5eLB4EBg4caOhz6tSpthl///33dbjdd9/dNgxv+ENAHM4899xz/iLgU0WJAEm3KNUWbqavu+46owGePHmybeRY64lez5IlS2zD8EbxINCtWzetT2xmsWDBAsuMY5cq6RWHsXGGZSIpvYgPGWDLoeR0VQCSbrr0bVtarL+VxnXevHmW4WTrOMw5UZKBwAknnKD1XrVqVWXlXxnLi6ReYPcqSjgIgGiBK0cQwsGzmGIh6RaTtiLOKyxU0RBUqlTJsjd75JFH6vvPPPNMxDlh9PlCALsHiVVto0aNlNV+ybvttpvW+4cffhh5ttLyQYchZbxrXPceeZWKXQIk3dippHAZwrxtkyZNdGNQv359tXHjxozMnHTSSfqeH//NMBbJXp+IzROwfRylsAgsW7ZMb1QPEoCOswWerHDPbgQkO7zf/2LN62Rb4DfuuD3Xr18/jSmNqOKmmejzQ9KNHuOiSmHVqlWqRo0aukE4/vjjM/LetWtXfR072HgR9F7QaNsdQXY/8pIPhrVH4JVXXlGlSpXSOrrgggsyAh511FH6OqzdvQiMsFq2bFnigKON6dOnl4hKDIvSMMcpZU1Lz76EslN8gaSbYuXbFX3hwoWqXLlyuqHt0qWLEax///76mtfN0aUHg8YcjYwc+C9ETAtOA+aC/ZgyZYqhj2uuucbIxymnnKKvjxkzxrjm5ofoXXScfTZ7ucKIB+6nZbhVsOBIj5ualKwwJN1k6TO00qAnIg0DyBaCDdFxzUzEbhIUcoUbvGyRtYr0wJONTGH+iwcq6HnkyJE6E6I/ryMSIFDEk613/BfLXbknc5xp6PnJMizMpVPShwBJN306d13ihx56yCDe4cOHK/nfrFkz13Eg4P7776/jQWOTLWhk0TDvscce2bf4v0AIyI5S0At8bg8YMEDryI3nMnOWnfQuc5rSswWxI3waBB8awBZlpqQPAZJu+nTuqcRDhw7VDQQaidKlSxu/8f+JJ57IGZcMG9otjRDSTUuDmxOwmAS4+OKLM3QNfeOAz274cM4lbvUuIxyoH9LrzRV3sd+XkYM0GIwVu66iyD9JNwpUExanWC1Lw2s+w5evkwipSuOaHVa++u3uZ4fn//whUK9ePUvihf7tnGlI7nLpXYaToXeMgNh9lEl8STrLEi1gREkfAiTd9Oncc4nFqMpMtubfThHKnK3V0gj0hsThRlp6OU5Yxe2eWcfZv08//XTH7DrpHQ9Kbw/h5HCMMEE3BcsEFYlF8YAASdcDWGkMunbtWtvejjQe2CrQTsSYJts6Gf8bNmyo46ZBiR16hbuONbmiX7uz08YX6MHiuWy9o0QyuoH7WB6Enm5arHhzjQAUTuNMOV8IkHTzhXSRprN69eqcja+TL2axUgXBYs2mEK005CDltDS4xVQF5s6dm1Pvv/76q22RRO+wgscaYBz4jWVCovs0jm7gAwM9e6uPEVsweSNRCJB0E6XOaApTpkwZo6GUBtN8tktV/MtKWDTE6AHhQMNjZc1sFxev5x8B0ZvVuUOHDrYZytZ79vMY2eB8pi18vJFwBEi6CVdwGMWTjcyzG0/8Hz9+vG0S+JpHGFkWYhuQN2KJwG233Wb7sTV//nzbPIveQa4yX4szerb80LKFjTdSggBJNyWKDlrMSZMmlWiAx40b5xgtGlqQLs6U4kRg1KhRGXrH5gczZsxwLIysweWSGEeYeDOlCJB0U6p4v8XG/O1HH33k6nExpuFQoiu4Yh3ovffes9z6zyrT1LsVKrxGBP5CgKTLmhAZAjIcHVkCjDiWCFDvsVQLMxUTBEi6MVFE0rKBuTs0vlwOlDTNOpeHenfGh3eJAEmXdSASBGQtJv3LRgJvbCOl3mOrGmYsJgiQdGOiiKRlA40v5va4HjFpmnUuj3iagv4pRIAIlESApFsSE14hAkTAJwIYXobhHB2e+ASQjyUeAZJu4lXMAhIBIkAEiEBcECDpxkUTzAcRIAJEgAgkHgGSbuJVzAISASJABIhAXBAg6cZFE8wHESACRIAIJB4Bkm7iVcwCEgEiQASIQFwQIOnGRRPMBxEgAkSACCQeAZJu4lXMAhIBIkAEiEBcECDpxkUTzAcRIAJEgAgkHgGSbuJVzAISASJABIhAXBAg6cZFE8wHESACRIAIJB4Bkm7iVcwCEgEiQASIQFwQIOnGRRPMBxEgAkSACCQeAZJu4lXMAhIBIkAEiEBcECDpxkUTzAcRIAJEgAgkHgGSbuJVzAISASJABIhAXBAg6cZFE8wHESACRIAIJB4Bkm7iVcwCEgEiQASIQFwQ+H+ua+rnDdO54gAAAABJRU5ErkJggg==[/img][br][br]Triangle [math]P'Q'R'[/math] is congruent to triangle [math]STU[/math].
Triangle [math]PQR[/math] is similar to triangle [math]STU[/math].
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAewAAADZCAYAAADi6gPKAAAgAElEQVR4Ae2dB/QdVbX/Hz2EFoogPURQpAUBBeQRQEAhPEIg1ICh80KTqgg8Hkh9goCaSAnCQ1qAEHoJRV4QTQi9JgRQMYZgqIYQEhA8//UZ157/+d3cfufOnJn57rXumntn5p7Z53vOnO8p++z9b04iBISAEBACQkAIBI/AvwWvoRQUAkJACAgBISAEnAhblUAICAEhIASEQA4QEGHnoJCkohAQAkJACAgBEbbqgBAQArlAYOTIke7iiy+OPrlQWEoKgYQREGEnDKiSEwJCoDsI/Nu//ZvjM2bMmO48QKkKgcAREGEHXkBSTwgIgX8hYIT95ptvChIhUEoERNilLHZlWgjkC4H3338/Gl1D2hIhUFYEVPvLWvLKtxDIEQLjxo2LCHvw4ME50lqqCoFkERBhJ4unUhMCQqALCJxzzjkRYZ933nldSF1JCoF8ICDCzkc5SUshUGoEBg0aFBH2Qw89VGoclPlyIyDCLnf5K/dCIBcIrLzyyhFhf/DBB7nQV0oKgW4gIMLuBqpKUwgIgcQQ+NOf/hSR9XrrrZdYmkpICOQRARF2HktNOguBEiFwyy23RIR94IEHlijXyqoQmB8BEfb8mOiMEBACASFw8sknR4SNpzOJECgzAiLsMpe+8i4EcoDANttsExH2pEmTcqCtVBQC3UNAhN09bJWyEBACCSDQu3dvt/DCC7svvvgigdSUhBDILwIi7PyWnTQXAoVH4LnnnotG11tuuWXh86oMCoFGCIiwGyGk60JACGSGwKhRoyLC/sEPfpCZDnqwEAgFARF2KCUhPYSAEJgPgcMPPzwi7Ouvv36+azohBMqGgAi7bCWu/AqBHCFgEbqmTJmSI62lqhDoDgIi7O7gqlSFgBDoEIE5c+a4HXfcMfp0mJT+LgQKgYAIuxDFqEwIASEgBIRA0REQYRe9hJU/ISAEhIAQKAQCIuxCFKMyIQSEgBAQAkVHQIRd9BJW/oSAEBACQqAQCIiwC1GMyoQQEAKzZ892Z511llt33XXdWmut5Y499lg3depUASMECoOACLswRamMCIHyIjB9+nS3xhprRHu2bSuYHceNG1deYJTzQiEgwi5UcSozQqCcCBx55JFVyRrSXmWVVcoJinJdOARE2IUrUmVICJQPARtN1zq+9NJL5QNFOS4cAiLswhWpMiQEyoXA22+/XXN0bQQ+ZsyYcoGi3BYSARF2IYtVmRIC5UJgqaWWqkvaiy22mDv66KPdM888Uy5glNtCISDCLlRxKjNCoJwIjBw5siZhE0vbRtocd9hhBzd69OhyAqVc5xoBEXaui0/KCwEhYAgQgtMnZv/7Zptt5nbdddce17EqZxvYX//6V0tCRyEQNAIi7KCLR8oJASHQCgKvvfaau/TSS90555zjJk6c6O65556YpCHsV155xZ100klu2WWXjc9D7EOHDnWPPPJIK4/SvUIgdQRE2KlDrgcKASGQJgJ33313TM6QNvL555+7K6+80m2++ebxNYh70003dZdddpmbN29emirqWUKgKQRE2E3BpJuEgBDIMwJ33XVXTMyDBg3qkZXx48e7YcOGxdchbozYjjvuOPfiiy/2uFc/hECWCIiws0RfzxYCQiA1BHzS3m233eZ77owZM9y5557r+vXr14O8d955Z6dtYfPBpRMZICDCzgB0PVIICIFsELjzzjtjMq5G2qbVrbfe6nbaaaf4XkbdX/nKV9x5553n2PctEQJZICDCzgJ1PVMICIHMELjjjjtiIh48eHBdPV544YVoanzJJZeM/wN5H3jgge6xxx6r+19dFAJJIyDCThpRpScEhEDwCNx+++0xAe++++4N9Z07d6771a9+FRmlQdj22WKLLdxVV13lvvjii4Zp6AYh0CkCIuxOEdT/C4MAU6R9+vQpTH6UkfoItEraltrDDz/s9ttvv5i0Ie/lllvOnXzyyW7KlCl2m45CIHEERNiJQ6oE84DAqaee6vj88pe/jNT98MMPowZ4zTXXzIP60jEhBMaOHRsT7x577NFSqtOmTYscr6y++upxGpA3VuislUuEQNIIiLCTRlTp5QIBm9LEuQZi65o43ZCUC4HbbrstJtwhQ4a0lfmbbropcnlq9Yrj1772NXfhhRe69957r6009SchUImACLsSEf0uBQLWsOJAA8GIaJlllnGMtCXlQ8An7T333LNtAJ5++ml31FFHuV69esWdgAUWWMAdeuihbsKECW2nqz8KARAQYaselA6B559/PmpMMRgygawhbUl5EWCvtXXkOiFtEJw9e7b7+c9/7jbaaKM4TdLeeuut3f/+7/+WF2TlvCMERNgdwac/5xEBrHppPI855phI/eeeey76/ec//zmP2ZHOCSLA/msj7b322iuRlB944AFHWpYuxxVXXDGyoXj99dcTeYYSKQcCIuxylLNy6SFwxBFHRI3nb37zm+jsmWee6eo50fD+qq8lQMAn7b333juxHP/xj390p59+ult55ZV7kDfGbvfdd19iz1FCxUVAhF3cslXOaiCwySabRA3m5MmTozv69+/v/u///q/G3TpdRgRuueWWmFSTJG3Dks7iNttsEz+DUfcGG2zgLrnkEjdr1iy7TUch0AMBEXYPOPSj6Ah88sknUSPJvlkTrV0bEjr6CNx8880xoe6zzz7+pcS+P/HEE44Zn4UWWih+1iKLLOKGDx/unnzyycSeo4SKgYAIuxjlqFw0iQDuJBnNfPe7323yH7qtzAiMHj06JtJ99923a1B88MEH7mc/+5lbb7314udRT7fbbjt3ww03dO25SjhfCIiw81Ve0rZDBGgUaQhZS5QIgWYQSIu0TRfid+PjnHpqn1VXXdWdccYZ7s0337TbdCwhAiLsEhZ6mbPMKIlGUJ6oylwLWs87jlGMPHFLmoZMnTrV/ehHP3IrrLBC/Gx0YHr+wQcfTEMFPSMwBETYgRWI1OkuAoRIpNF76623uvsgpV44BG688caYOIcOHZpq/q6++mr37W9/O34+dXjjjTd2I0aMcHPmzElVFz0sOwRE2NlhryenjABxjGno+vbtm/KT9biiIOCT9v777596th5//HF38MEH9yDu3r17Rz4F8CcgKTYCIuxil69y5yHA2iCEnZRDDC9pfS0RAhiBUY/4ZEHaQP3OO++4Cy64wK2zzjqxLuiDMSXW7ZLqCFi5Vb/6r7Ns8eS+EH0ziLDrlZyuFQqB//7v/45eRAIySIRAJwhcf/31MVEecMABnSTV8X8JE7rLLrvE+kA2RJ07++yz3fTp0ztOvygJGBGz/72e4EgJDDmGJiLs0EpE+nQNgZ133jl6EeUkpWsQlyphn7S///3vZ573l19+2Z144olREBsbSXJkFuDRRx/NXL+sFSASH3gcd9xxdVVhZM19IbYTIuy6RaeLRULAGrGPP/64SNlSXjJE4Lrrrosad+pWCKQNFJ999pm74oor3Le+9a1YN/T75je/6S6//PLoeoaQZfZoHCSBQ6PgKwQC4r4QI/eJsDOrPnpwmgi8+uqrju04aW3JSTNvela2COBmlAaez7Bhw7JVpuLpjBKZsjf9OC699NLuhBNOcC+99FLF3cX+yTIB+a8X5Idr3MO9IYoIO8RSkU5CQAjkCoFrr702JsUQXd2yjfGcc86Jdkj45D1w4EA3duzYXGHdjrKMlsk3o+d6cscdd0T3hViG6C3Crld6uiYEhIAQaBIBn7QPOuigJv+V/m0ENvne974XdzAgsrXXXtudf/75bubMmekrlMITmzU4Y30bPFjvDlFE2CGWinQSAkIglwiwPmoj2JBJG3Cff/55d+yxx7olllgi1hnd0ft3v/tdLvGvpbRZfm+77bburLPOqvnBRwMYhGhwRt5E2LVKWOeFgBAQAm0gcM0118QEiJOT0IUIdiNHjnTf+MY3Yr0hrS233NL9+te/dv/85z9Dz0JD/czy2zpTjY4NE8zoBhF2RsDrsflEYNKkSdE2maWWWsotv/zy7uijj65rxJLPXErrThHwSfuQQw7pNLnU/v/QQw8587dvpEY9/+EPf+gw3MyrmOU3I+daH9v21b9//2Cz2TJhM+XDtAJ+bClQvh9//PFqtIIt4uQVM0tKyh8jjXpiPdtQp5jq6V55jYAh1oj5R1xDvvLKK5W363fJEcD/t9WTPJE2xUZUMBwNrbbaanEeyAvv81133ZWrkrX2qpHlty1nNNqnnWXmmyZsGmab37dKaGby9rvR/rYsM6pnJ4eAWVLaC1wvZasj9e7Jy7U+ffr0aLys3nPM2ttVXjAsm55MKVs9OfTQQ3OZffynf+c734nzQX7WXXddd9FFF7n3338/+DxZe0Vno540u0+7XhrdvtYUYVvPg4IiU/4+NszlLaNclwP6bhdZ9umbAYc1RLUcDFjPNuQppmbRfOGFF3o0WJZ3//jFF180m5zuKxECPmkfdthhuc35U0895Y488ki36KKLxu/Cggsu6MjTxIkTg82XtVeNLL9pp0LnsIaEDQFbo1RvBI1/Vu5r1IsJtlSlWNMIWFk3ehGsZxvqnsamM+yce/jhh+P3wN6HyuMbb7zRSpK6t0QIXHXVVXH9yTNpU2SzZs2Ktj1tuOGGcZ54FwYMGODY2haaWHvVaFmOPDTap5113hoStmWWxrme2GiKTNcacdX7v67lBwHKmKluK3PsGaqJEXq9jl61/4V4bu7cuT0aJzCo/PTq1csdddRR7umnnw4xC9IpYwRGjRoV15nDDz88Y22Sefz999/vhgwZEueLd2KllVZyp512mgulA2sGZ/VyDJmjO3wXstQlbBshkeFmSNgasEY9mZABkW71EbAZF6vY1qGrthRS71r9p4R5FUtZq+OVx8UXX7zHtR122MHddNNNYWZEWmWGwJVXXhnXkyOOOCIzPZJ+MOQMSUPW/rsBmUPqWYm1V42W5cxCvNHANKt82HPrEratTTea+7fErIEWYRsixTuaPYNVbPtdzbLSXtwiofCf//mfPRokyyNHDHN23XXXHtdXX331yEnDtGnTigSD8tIBAj5pU5+KJkyLMz3uvxtMn8MjH330UarZtfap0bKccR2D1JClLmHbVEK10VO1TImwq6FSrHPmus8qNjMv1BMsqH2xni11omjCUgBrkjfccIP74IMPoug/1jjhJWry5Mnu5JNPdssuu2yPRovAI6yFS4QA0bSszhSRtCnhCRMmRAZpCyywQJxXDNYwXMOALQ3hXWUAybGe0F5xXzMzyfXS6fa1moSN8lahmlXC7tcIu1nE8nefWVL6L0C13qn1bKuNvPOX68Ya+44yzLsVVuOsW26xxRbxu8Q7summm7pf/epXjnVxSXkRINSltZnDhw8vLBBs/brwwgvdqquuGueXfDMjxZYxSfMINCTsZkdI9Eys8vmNefOq6M48IEAZM6L2xTp3/g6BypG4f39Rv1cjbcvrY489FoVetHeE45JLLunAiS1jknIi4JM2I88iC85jWEobNGhQzBW8BzhnwUnLX/7ylyJnP5G81SRsMzhrlrDt/kbeZBLRWolkgkA1YjZFzEGKTSlVG4nbvUU+NvJu9fbbb7vzzjvP9evXr0ejtdNOO7kxY8YUGRrlrQYCl112WVwXikras2fPduutt577xz/+EaEwZcqUyN3pcsstF+cd8sYtKu5RJdURqEnYNqXZLGHbtGijxf3qauhsHhCoZ0lpW7jMQJGXr3Iknoc8JqGj7yijnncrCHrnnXfu0WBB5Oeee66bMWNGEqoojZwgwBIJ7wwftgYWTejs21KRnzcCi2APQqARyz9HApEQkITAJJXCoOC2225z9957ryubs6KahG2jKcBrJEyBG9j8T1JMBKxTVq2MrQ6wJ7vIBmfNlqzvKKMeaZPeiy++GE2NE1DE3iOOw4YNc+PHj2/2kbov5wj4pE1QmSIJ5HvxxRfXzRIhPa2NsfeA0J+EACUUKPKjH/2oxzvCfT/72c/qplukizXZ2F+TrtZA+yCwdglwzY7G/f/qe34QqJz2rtSc8qce2Gjbtn5V3leW3z5pN+Pdat68eY7pUYzSrMHiuPnmm0fGa59//nlZoMs8n7a0k7YiEJuVfZFIGx8GtrOkEaZ/+9vf3Pnnn+++8pWvxFiASeVvw4njdddd1yjZQlyvSdjkzhpgInLVEr9H1Oz2r1pp6Xy4CFgHrp4DAltGsRepUUcv3Nwmp1m73q0eeeQRN3To0B4NFtvETjrpJEUGS654qqbEAKRym2LVG7t0csSIEXG5H3PMMV16SrrJst3x97//fcsPZep74MCBMR7WtlQeMeAsg9QlbAjY9mJD2oQXRJj+5DvnDDgaa0lxEYB8Ket6NgqQutUX7s1qlBJaKfiOMlr1bvXXv/41cryyxhprxO8a2OKgpdkRS2h4pKEP9ZX2yWwqaj2TWSDus86ldUyzNp795S9/GZc3U8J5l7333ts9++yzbWejcjBgvOMfMegsutQlbDIPadtUqA+OfeeaVfaig1Xm/Nk0d6MG0GZcsm7wQiurTkjb8jJ69GiHy1N79zh+9atfdT/96U/du+++a7fp6FxkEwA+jepr5W4GI4YQBiA+af/gBz/Idbli/d2Jj33WsP16X+17NQO1XINWRfmGhG3/oQLTGDNNzof9o+rhGzrFPzKrQses0ajZ7tPyyPx1IinvVs8884xjfbPSfzn7XP/whz/M/+ASnrHlvEaDCRp+fzcDbRy/G9XztCD9xS9+ERNVnkmbmaVHH320I9gWW2yxGItKwt5jjz06Sjsvf26asPOSIekpBEJGwHeU0al3q48//tjRoNso0Rqxf//3f3c4cSmzGBb1MIDMuQ9yN4GsQ/PO9/Of/zwmqtB0M9waHXGM0qlXs5tvvjnGwcrXjk8++WQjFQpxXYRdiGJUJvKEQJKkbfkeN26c22uvvXo0aF/60pfcj3/8Y/faa6/ZbaU4MrtDQ17PQBIgbJnHdjPY/5glCk180j7++ONDU6+hPr/5zW8iW4yGNza44cEHH5zPd8Hdd9/d4F/FuSzCLk5ZKic5QqBb3q3+9Kc/uf/6r/9yK6+8cg/y3n333SNHEzmCqG1VbR260WjUtqPa0h73++5121agS39kPd5GlHkjbTpDgwcPTgwZtkCaj36s6ssiIuyylHSVfDKNdMEFF0SBKOTHtwpAXT7lO8rohncr9qb6Ozlo7Ndff/3IgUUoa7TdgNgMHxsZjpkxrWHBiLzRmnc39G0lzUsuuSQm7RNOOKGVv2Z+77e+9a1EPfj95Cc/ibBg21dZJHXCxrQff7nrrruu23rrrR2xUyXpIkBIyGp7G3FuIEkXgW6TNrmZNGmSw+hn4YUXjht7vhPWkWtFE1vTZxoZT3G1PnRg/N0MjSzKQ8HJJ+0TTzwxFLUa6nHqqacm2t4z4KAMCd85Z86chs8vwg2pErZvJWtTOxx33HHHImCZmzxgTezj73/HO5ckXQTS8m7FSBL3kARh8MucUfj111+fbqa7+DQ/b42+hzwFXg8iytHylhfSxnEKSzOVguFku2KzJDhYKYOkRtifffZZXMGsovlH9qmGLjiqx9k8EWc+/fTTKJ4xe/+w1v3oo4/crFmzou0gxH9977333DvvvONws0cgh7feesvhBIOp5zfffNOx1vjGG29EBkFTp051RK955ZVX3Msvvxz5lmbfIbMRbOEh2DsjoSeeeCIKCk/Ff/zxxx0hG5nC++1vf+vwjEWUG4yPHnjgAXffffe5e+65x2GQgZOb22+/PXKY7wem8PG37yussELoxVBI/dL2bkXdoPG0cue4yiqrROvfIRpdNVvoZvlNQ44xWa2Pbfsyg7Nm0w/pPnxoW/nhAS8PQp0z//i0Z2zHYmqfdrIdYacFGDTy199O2iH+JzXCxumDVa5qRwIfbL/99lFQc3r8AwYMiKbMt9pqqyiSC/6UWQPZbLPN3CabbBJFc2Hqa8MNN3QbbLBBNGpgmh1HEuuss07kd3attdZyffv2dXiJIuYqAdQxxllppZUcFrSQE+HdcEPIdg50wNl87969Xa9evdyiiy4aTSMutNBC0bRLNb2LeI4OhyR9BNImbXKIBfkpp5wSvQ9+XcYzFZ2/vIkZZjUiYiPs0NesG+F/0UUXxe3qySef3Oj2zK9j4Pf973/f/c///I+jbb/rrrs60on/U2/pbJZBUiNsMxDwG4Uyf2fdZcEFF4w6BHQM6CDgCIMOAx2HpZdeOupI0KGgM8F1Ohp0OKicdEDoiNAhoWOCY3w6KnRY6Lgw7YmBER0aOjaEq6OjUzkdWlkGiyyySBnqfbB59L1bpe2Skr3bNKJ+naDuoBOzSHmQSsvvWjrzTpHPIohP2qHbodBBog0bMmSI+/vf/94x/Mzc0n5SlmVwGpRajX344Yd7NAR+o2DfV1999SiAOYY4GKNh5XrDDTdEG+4Zod9yyy3u1ltvjaZ2meJlqpceFtN7TAHff//90aiAqWGex1QxFYSpY0K3MZU8YcIEN3HixGiKmalm3OUx9cwUNGEOX3rppWhqminqV199NRqBMHXNFDZThUxpM7U9ffr0aKqbqZyZM2dGriEZmbJOSEVkipxGDmOIuXPnRlPoVC4iLjG13oqgG3tsk5LKoPGGP8eiBBtICqss0snauxXvSaWdA51JvKt14g86DSxtTbPetD7XqOt0RooiF154Ydy+hkjatIPMeuBaF5uNb37zm1UtxtF98uTJLRWLddLYzlh0SY2wAfJrX/taXKl8kqj8zsiTBgOSlbiog7DddtslBoVNI1Xizm8shyXZI+A7ysjKJSX+yZm6ZNbGrysYidKBDk3oLKMno+d6Yvu02f5VJMGnvJUTcaNDEQZSLEGcc8450cAFvfBDQBvvCwO1dsrEjJkJS1t0SZWwIeB+/frFlcoqFz0vGgemdpjGtfMcWbemIMtitl+twjEiZ5obY7ekhJkEyJlZDRrk//iP/4hxpwcsyR4Bn7QbOQHptrbMaPl1hHeTJRmWuphxCkHM4KyR5TdYon9etnG1gq1P2tgmhCDTpk2LjGQrdWE0jSc+xEi9HeMzZj2NM+rNrFQ+P4+/UyVsAwgTfEYN7CfEYrpSMHYhuosVAkem5Ni/XcR9o5X5r/Z70KBB0XR9tWtJneMFN8x5gSTZI2BGVJRLCN6t2MmARTKxua2ucCR2N0tQWQodf3Rp1uCsqAFqmBWxsgmFtGvVC5bgsPDeaKONoqXKWvc1Os/Ajjwzci+yZELYzQLKVqhzzz3Xrb322nEFpFAIbsD2JNaDyyJnnHGGwx9vt8X8UWNBzxq+JHsEfEcZoXi3YraHrZjs3jBy4MguDhpNtj2mLc1afpu+aeuX5vPwYGj5tFFsms9v9lm4GMVYlja9k9GxddaIE19kCZqwfeBZd63cN8p2LKa3itpT9vPPiBdvVd0WDORYC+Jlp9eKoZwkewRCJG1DhalotuoYQXBkpwMzAhhypiXMRtBwm6vRas/lGvc0clta7b95O+eTNl7GQhTa7/PPPz8agLE9F0PjdoQ93dQ7PPjRCSiq5IawrQCw1iZUG+tnfgPBHu4ieWuy/NoRImVLVhp7pJn2tClPliYkYSAQuncrtoXRyau0U9l5552jnR1hoFguLSBDaydPO+20oDKPjcbhhx8e60S7w2+ChDBAa1XY6kpeLZhLq//Pw/25I2wf1DFjxrhddtklrpAU1oorruiwkGx1a4CfbqjfmdpiKSANYatcqC96GvkP9Rkhe7diPZKtlgjbL3faaae4DlGX8BVw3nnnte3VKtQyCV0vMA/tXYaQ2eJVbQCCLcRBBx3k2BlDfW92KyFkTz7TmInMqsxzTdgGGnumMa7AsYhVTI707Nm7XRSh4n7nO99JLTv+fuC0OgqpZS7HDwqVtDfeeGNHYBlf8CGAgemSSy7Z491k+w7+ESTpIIAtkLWNp59+ejoPbfAUfGDUEwZdLAVh9Y/Tp2HDhkXLGexiYTbn6quvdrRRTPfvs88+0Y4X8sjOl6JKIQjbLxwcrdBzs8ppBYjRFg5Q8i6MYqisaYltgQHHRx99NK3H6jkNEPC9W4XgkhJirhfvmCUdtmfS8PrvJjGNCTiDj/5aUm0nSa17db42Aj5p583JCCNxHPrceOONjql01uexhoe8mc3BCRb34Eaa+sWadhGlcIRthfTCCy9ETuVtLdYaCRoVm7aze/N0pNfJSObtt99OTW0sL8EPX+xqPFODveGDQvJudfPNN7tm10jxQrjffvv1IG7eUzoezJaZsMd7scUWi+7DZS4k06qXQEtLx38hgPMSawvzRtrNlKH5Cmi0ta+ZtEK8p7CEbWDTc2fqhNjbVlE5sp5G5Q3F6YPp28wR385p+pnG1ao5tAFHSTgIhELaOOwYNWpUS8Dg8IKGlSlM/93E5wCuK/1z9j3NJaGWMpOjm88+++wYW2YeiyTM4lBXMH4sohSesP1CI+D5UUcdFUXjsgaAI+sfeXMUglHG5Zdf7mevq99ZP8d5DXi14z6wq8qVPHHfu1VWLikZHXcyc3XTTTdF0fr897LW97LEPu5mtfZJm103RRF2EVm9oUNYNCkVYVvhsZ4G2VU6fWDbFCMW4liHLsTYJgxprS0MWEwmvWZPQ2kvA9OVknAQyNq7FV4IicneqWCIRIQ5q2fVjuowdoryv/7vR1AsEmmbHwl8jBdNSknYfiFiyIBrPDNWsAYCRxBZu1r09az2HUMfjHiIVOYLSwDd2trgT8EWed+7j2devmdJ2sOHD0/sfdl///3rEnYjX+F5Ka8Q9DzrrLNirIuy7svaPO14PSPIELBvR4fSE7aBxjot1ocYdBlpcySONOeTiN1qz0ryyDQ/7iBt+xqjaqKiVY6u8QaXVLxYGmewIaZ3UmkmiUmZ0/K9W6XpkhKXqezdT0LwduW/g5Xfi+4vOgkMW0nDJ22+511ok6gzxMlOMmBSCO4DdpIAAB42SURBVLiIsKuUAiPrSleLuLw77LDDoq0FVf6S6amXX345clLB/lxG1tX2TNPp4HoSgo93LMZ5KTDeS9NiPQn9i56G790qLZeUbBlK0t1nrVC8GKjJUjz5Gszo2jpGRVjuWmWVVaL83H333cmDlWGKIuw64M+cOTNa02Zt2yozR9a+WQNnLTwUYQbge9/7nltrrbWqRvXCD3sjRwXN5IWRPGtETL9aUBbiI0vCQiBt0iYwTZINPeFfLQKTvXts/UqiDodVUuFowzq2YZ1kWWaRQ5Y5yQu2FUUSEXaTpYkV+d577x1XaCrDEkssEVmdMy2dtWCExnQ+U6KsazPisZEv1pJEw+lECPDA2uIBBxwQuwqcMGGCW3DBBSNMiK0tCQuBNF1STpw4MdpbnTQCU6dOdcRN5n0jgpykuwiwzctIG0vyvIoZyPbt2zevWaiqtwi7Kiy1T7Jvm/3bTAVbxeY4YMCAaL93PY9NtVPt/AqRkUaMGBElhHtIRsDMDLCOyUvYjjtCrOXxHLfnnntGBhzVtu1w3XBge5EkLAR871bt1IFmc/PJJ5+4ddddtyvR3ZgCp3NMPaPjKOkuAj5p09blUebMmRO3S3hBK4qIsDsoSQgMS0QjLI5M22GAg6e1tIStXZBqpTBNjhtTeplf//rXo1CkrG+PHz/evfbaa+7dd991H330UWRQR0eEvdakxSid2QQM7hjdNPL57O/pJCCLJCwE0vJuha/nbrmvpX7zfmW1zzysEu2+NmZpDeZ5Je2BAwdGdSbPMwWVJS3CrkSkjd9YZFPBLbybETg+zRmBdlswGJk0aVLVx0DIjLRxKUqEHKZJWd8hytlWW20VrUezVkhkHEj6pJNOcldeeWXN9Ko+xLkoug757tWrl3vmmWdq3abzGSGQBmlfe+21USCGbmSRjib1iz3aknQQYEbG2jJmavImeIRE/y233DJvqtfUV4RdE5r2LmCURZQwq+gcv/zlL0fRxHw/ye2l3vq/2GqTluEFywLklw7Chx9+2Lqy+kdXEfBnQrrhkhIjzQ022MAxPZ60sDPB3qlXX3016eSVXg0EfNKms58nef311+M6M3369DypXlNXEXZNaDq7QJAOpu+Iz20NDUdGtmlOG+My0vZod5ajxv/GuM1mGXDCLwkPgW57t2KGpnJ7F8tDRFTqVL797W9H79Kll17aaVL6fwsIENTF2rC8kbb51SAiXBFEhJ1CKeIIgqAFVuk5rrHGGo5tFPi+7aYQROFvf/tbNx/RI22MgiyfxEGuJ5UNe717dS05BLpJ2iyHsLxiwvbH/v37O6J5dSo2rf/d736306T0/xYRYD+/vddsGcyLmN577LFHXlSuq6cIuy48yV7E2xjxpZdZZpm48vMSsEea9eVuCNaSaQuuUe3lxmFLNbE9n91yoVrtmTr3/xHwvVsl7ZKSOk6nAOdDLMdMmzbt/z+4g2/swbZ6NWvWrA5S0l/bQcDIjzLAMDUP8rvf/S6qMwQuKoLDHRF2BrXu888/j7yRsTfaGiCO66yzTmQUxnpd3sVf+6r0NuR7kTvmmGPyntXc6u97t0rSJSUjMOJYd2PqGsdAvCtJjNhzW3AZKs42UWuz8kLaK620UqRzZcyFDGFs+9Ei7LahS+aPTzzxRDQKsdCV9jLsu+++bty4cck8JKNU9ttvv+hF6dOnj8N96p///OfIgYvl8eKLL85IMz3WEEiStDHyOfjggyMXvqx1EjGuUvDtjM8AOq3tCOFxqT+K2NUOesn855RTTolJG38PoQuhiKkzRRgciLADqW1MXRN8nTVnIzSO66+/vrvooouiPdOBqNq0GjTOFsKU2QPz79u7d283duzYptPRjd1FwJYnqG/tuqTENSn+v327BMi10n89ZN3Jvl52PaAnxpyS7BDAoNbaqdAdJmF0i679+vXLDrCEnizCTgjIJJNh3eWQQw6J3X7ai8GoIm+ennAtudRSS8UvNx0QHLRIwkLA927VjqMJbDAoa1/wATBo0KDIeQ/n6Xh26sKWkTl7/XkneE8k2SHgkzZhd0MV6qG1oXlve0TYodYy5xwuRlkHxMrWKhxHfIXjFICKGLr4RIDuGCRJwkTAL6t2SLtartjqh1U30+Ns9UuizmKkSV1KKxJZtXzp3L8QMD/vlEfIpE1gJHTM27a0ynomwq5EJNDfDz/8cBR8g0pnn0UWWSRqCEONSU2gENN1m222ib9fccUVgaIstbrhkpLlD+wYkuqsjRo1KqpL7LGVZI8Avh7sPWcWJURhtwo6dhoEKeu8ibCzLoEWn8+eagw9CLRgLwlH3O/hUnTevHktppj87bWMy3CqYTo/9NBDyT9YKSaCgG/h36lLSvwMYMfwwAMPOBr2ffbZxz3//PMd6ck2MatHGLpJskfAJ+1Ku4XstXPRco3VGYtiGIJereogwm4VsYDuZ5vCXnvtFTdeVMgll1wysobMKm4wwR9WXXXVSCciLN1+++09ELPpTLZa4INdEiYCSZD2p59+6oYMGeLwMW7CdqzNNtssmpp877337HTLxy222CKqYywNScJAwO+Qh0ja+KGnjSQgUl5FhJ3XkvP0Zp0Q617bo2o9Saahfatd7y9d+0oQkoUXXjiybsdRTKV8/PHH8Zo8swJFcGZQmcei/O7UJSWe7qqtGWKbwXkiyHFsxze4OX7Bb78kHAROPPHEeAAR2rZN247GICevIsLOa8nV0JsRLZa5Rtocl19+eceL9OKLL9b4V7KnR48eHYXsrJUqepjl+P7771/rNp0PAAHfu1WrLikJ2VpPZsyY4S655BJHx5JGlG2NzAx99tln9f7m2C6Iu1+r43QCJeEg4JM25RuKmNtkZiHzKiLsvJZcA72Jd820pk1PW+OGxe5NN93U4N/dv8yLbDp1I3JU93NQniek4d0Kw0lsM4h7jX0GVr04vMBQjfVRjvzmPPu98Q2NIRt1KM1gOuUp9c5yesIJJ8Tvd0ikvcIKK0R6YVORRxFh57HUWtSZEe9OO+0Uv0A0ciuvvHK0LaZy72yLSbd1+4QJE6JpcfaaG2mnPXXfluIl/lMapG3wfvHFF5F9w+9//3t3//33R372OfIbuwfzksaebuoP9UgSHgI4ybH3uxtuatvJsblFbhSYqJ200/iPCDsNlAN5Bu5BGa1YL9NeJvbH3nbbbYlrWW0k/9RTTzmMPx588MHoebgLND0ee+yxxHVQgskhYGuAlFcILinvvPPOqO7Q+ZSEiYBP2rUCAaWpOW0S9RfPi3kUEXYeSy0BnXElSRhEI0uOffv2dRjzvPnmmx0/4ZVXXom28NBBMGcZbPcipjHuJX0ZOHBgpMeaa67pGq17+v/T9/QR8L1bZe2SEit0fBFQdxl9S8JEgOUMa2eyJu0PP/ww1oU47XkTEXbeSixhfYlfzPTQ0ksvHVdkXi6241QSazuPplEnFvj48eMjw6JqU99s72Fdkuf6sZTbeZ7+030EQiJtM7DEXkMSLgK0MUbav/jFLzJVdIcddoh0CWGWqFUgRNitIlbQ+7HMxYMUI2B7sTh+9atfdVgHY9HbruClbY011nA77rhjzSSefPLJeLR06KGH1rxPF8JAIBSXlJdffnlUX3HXKwkbgWOPPTZuW7LaP4/Dpm233TbSg90JeRMRdt5KLAV9J06cGAVpIKaxT95Dhw517Xgou/feeyPrXqbGcFeKBXs1wamGPa/a/t1q/9G57BDwvVtl5ZKS5RurM3hVk4SNgE/aI0aM6FhZBhnM3tWTKVOmRIMOnO0QQIm6anXmnXfeqffX4K6JsIMrknAUmj17ths5cmTkmcoqOEeMxnCK8P777zdUlnVGerS2xsj+WRxmQM7VhNG8PQvrdknYCIRA2haSln3ckvAR8A1NOyVttmfttttuVTMNkR9xxBGR/3DWzrGhMVlvvfWidgZbnjyJCDtPpZWhrlR+CwRvhMqRc/V6uBA7ASV8wVodn9K15LDDDoteJjym4TlNEjYCWbuktHje7HaQ5AOBo48+Ou6YMyjoRJi5Y2nEBAcpzORB5LX26FtHc99997W/5eIows5FMYWjJKNqSNj88hp54x+aF49RuQnr3hiTtbP+jaEaabOG/u6771qSOgaKgO/dKm2XlOzrp64stNBCbu7cuYEiJLUqEfBJu5PZEZZFaGfGjRsXLeXtuuuu0d79yuf5v3/7299GdWaZZZbxTwf/XYQdfBGFqyB7qVnXNtLmyLo3Di1YB8cKs11LzLfeeivaZkaaOH2RhI9AlqRtHv0qg82Ej1q5NTzqqKPi9qNd0saRDkGFVlxxxchlbbOILrvsstGz27HLafYZSd8nwk4a0RKmxwiatWfbmmUETrQugto38g1dC7LHH388fpl5sSXhI5CVS0pbRjn88MPDB0ka9kDgyCOPjN/zyy67rMe1Rj+Y/sbdMstuu+yyS+QZr9F/7LoNNqizeRERdl5KKid6snebPdxG2hzZ480+TPZ8tyoYhVhaIYbsazU/Zbjf926VlkvKsWPHRvVktdVWKwPEhcujT9r+enS9jDIYwKCVbaMInhLZOopr22bkhhtuiOoMvuvzIiLsvJRUzvTEIhOvaXhPM8LliGOUVi0zzzzzzDgNTXnmoyL4pJ2Gd6tPPvnELbjgglE9YTmmmsiLXjVUwjk3fPjw+D2vR9rTpk1z+ARnCWbWrFk9MkB0uWY79jhssrbppZde6pFOqD9E2KGWTIH0wk85hiD2cnDEnzmWmliMNyNYffI/QuM9//zzzfxF92SMQNouKZkSpY5gNW6C7/qzzz7bsQeXa9qrbciEebSALpTVFVdcMZ+SLJNtueWW7qqrrprvGifYV01Et5kzZ1a9XnnS3DMzWs+DiLDzUEoF0ZHIYPSACdbAC2kfXrBm9lybF7aNNtoo9k9eEGgKm400XVKyS4E6RWAHbB7WWmutuI5ZXWvXsKmwBRRgxtg7beV15ZVXxhqyRat///7xFHh8oYMvEDXPyotLZBF2B4Wtv7aPAFFzMBaxF5Mjlr74hH799derJvzHP/7RffnLX47+M3jw4Kr36GR4CPik3Q2XlBg9/vrXv54vhKzVLdY1icn86quvhgeONKqKQCVpU77bb7+9S3rqmvSsnjTjCKqqsimeFGGnCLYeNT8CL774YrQWtfzyy8cvDi8QQR2qrVdjYGIvGGtYknwg4LukTIK0n332WYf72q222iquD1YvOG6++eaOTuHf//73fAAkLedDAIt/K1NG1t2yQcDojOdghBa6iLBDL6ES6UckLxzy20vKkWnNn/zkJ+4vf/lLjATTZHZPp16S4kT1pesIJOWSkpkWK3874moSm4j9998/ukaHT5J/BGy7HuVca92601zaVkTqTugiwg69hEqo39NPP+1o3DEwswaZ41577eXuu+++CJFTTjklvsbeTUgdg5VaPspLCGOQWfZJu5PO1je+8Y0obCsWwcReN8FnPXVl0UUXbXv/v6WlYxgI+KTN1HjSguMU6sxyyy2XdNKJpyfCThxSJZgUAvPmzYssRbEK9YmbKSw8qFVants9GB0RrlMSJgK+S8p2SbveeqMZNd51111hAiCtWkaAkLv2fneDtPEVQfq4LA1ZRNghl450ixH4wx/+4FjTYuRkL269I5bkknARSMIlZa3cHXLIIVEdYV+vpDgIWLny3l999dWJZowgIKTLskrIIsIOuXSk23wI4CgBo6VNNtmkIXHXcqAxX6I6kQkCPmm36pKynsK33nprVDfWXHPNerfpWg4R8En7mmuuSSwH5lFx/fXXTyzNbiQkwu4GqkozFQQajbbTcouZSmYL+hDfJWUrpF1vPzUR42z2RUsjxas4Bx98cFy+SZE2DleszkyePDlY0ETYwRaNFGuEwNprrx2/ZPay+UeiiUnCR6BZl5R+TrACJ5xiNcGX9KabbhrVDYwRJcVD4KCDDorffXaXJCEDBgyI0kw7PGwruouwW0FL9waFAD6qfYL2v+ctzm1QwGagTCOXlJUqEaUJD3m+TJkyJXJDynKJGSriklRSTAQOPPDA+P2/9tprO87kBRdcEKW3ww47dJxWtxIQYXcLWaWbCgJ4sfKJ2r7jv1ySLwR80vZdUtbKBVv7WPZgWxfBRnBdO2LECEcs9ddeey2uF91yuFFLL51PD4EkSfuFF16I68yHH36YXiZaeJIIuwWwdGuYCFx//fWOXjHToD/+8Y8dkcIk+USg0iVlvVxQzriq3XDDDSOr4X/+8589bsc7Fh24UaNG9TivH8VCYNiwYTHRthoJsBIJtoRSZ/CSF6KIsEMsFekkBEqMgO+SshbZYp+AV7zdd9/dYYRUTei80fhyj6TYCBBu02bXrrvuurYza37vSS9EEWGHWCrSSQiUHAGftCtdUl500UVRIIjHHnssQok9tNX8znOdRrxXr17u888/Lzmixc++T9rMurUjDzzwQFRnCP8booiwQywV6SQEhIDzXVJC2p999pnDSxof9uObTJo0yW299dbuk08+sVPxccUVV4wa4HvuuSc+py/FReCAAw6IR9rtkvYSSywRpTF+/PjggBJhB1ckUkgICAFDwHdJSQQuInRVE7ZvVbtmRkmQvKQcCFgAGGZX2onARcwC/otRY2giwg6tRKRPqggcd9xxbtttt40+zz33XMNn33HHHfH9kIGk+wj4pF3LJaU/4vY1IhgMjW+/fv380/pecAR80r7xxhtbyi3OWKgzIbo3FmG3VJS6uWgI4L6Sl5NPMw4Y/PtF2OnVBt8lZS3SrqYN8bCtfJ955plqt+hcQREYOnRoXPatkPbbb78d/2/q1KlBoSPCDqo4pEyaCLAtiMbctv+ceeaZdR/Pnl/uN9KW69O6cCV+sV2XlLZX/9xzz01cJyUYNgL77bdfTL6tbNXaaqutov/hnCkkEWGHVBrSJVUEmN6GgJkW51hvxIwjhT59+kRkvdtuu0X3421Lki4CPmk3MyOCdpdccklUXjTCkvIh4JP26NGjmwIAewjahEpvek39uYs3ibC7CK6SDhsBRtS8lEbc7OutJXYvJIHbU/4nyQaBVv1I47KU8uIzY8aMbJTWUzNFwMJnUgeaIe1nn302rjMfffRRprr7D1er46Oh76VCAILmBWZqnGnxvn37Vs0/1xldc78/jV71Zp1MBQGz/qb8mvEjvcEGG0Rl3cr6dyoZ0UNSQ2CfffaJSRhjxEaCoSL165Zbbml0a2rXRdipQa0HhYYAI2ULEmLkXU1HIwemwBlh8xLXmz6vlobOJY+AlQvl0cgl5Q9/+MOo3Pbcc8/kFVGKuUFg7733jkm7ERGzFZC6xYxOKCLCDqUkpEeqCLCFi5fRpsFtHZsRtC82ombdGrH7ZHDmo5Td92b9SD/66KNReeMUQ1JuBJol7XvvvTeqMyuttFIwgImwgykKKZImAjZSNstwW6OuNCSzkbcRuf1uZs92mvkp87N8l5T1/Egvv/zyUQN8//33lxku5d05Z85R6LTfeuutVTEhmMziiy8e1ZnHH3+86j1pnxRhp424nhcEAjZSxuAMMcMz+805yJsX2p/+5jcfSVgI+KRdyyWlua089thjw1Je2mSCAMsj9j6PGTOmqg577LFHdM+pp55a9XraJ9XypI24nhcEAjZStpGzkbONuFGSe1jjtti4dg/nJeEhYIRMI1zNJSXOM7i29tprh6e8NMoEAZ+0b7vttvl0wIc9dWbjjTee71oWJ0TYWaCuZ2aOAC8hDlBMIGXOMfJGKqfMOWeOU+we+6+O4SDgu6SsJO0PPvggKmPKWUsa4ZRZ1poMGTIkrheVpD19+vT42htvvJG1qk6EnXkRSIG0EbCRshmS2fNpyG30DJnzsdE195hVMmQuCRcBn7QrXVJuv/32UQN8wQUXhJsBaZY6Ajb1TRswduzYHs/fYostojozYsSIHuez+CHCzgJ1PTNTBGyk7E9/oxB7sZn6suuVxGwuSTU6y7T4mnq470fad0lJLG0a5QEDBjSVjm4qDwI+afvx1c8+++yozgwcODBzMETYmReBFEgbARspM9L2xda1zQWpf82mzGnsJflAwHdJaaT98ssvR40v5Thz5sx8ZERapobA7rvvHtcPI+2nnnoqOrfAAgu4OXPmpKZLtQep9amGis4VGgEL9uFPd5Nh29pFY15J5jaNblPmhQaoQJnzSdtcUn7961+PGuBmPKQVCAplpUkEBg8eHJO27Rqx2bXKNe4mk0zsNhF2YlAqoTwgYCNlSLtSjLCrkbJdq5xGr0xDv8NDwPcjjUvKE088MWqQcVUpEQLVELAAP3Te77zzTjd8+PCozhCbPUsRYWeJvp6dOgJs44J0K9enUcSuVVujpqfN/6pdSz0TemDLCPh+pE8//fSo8cXr2UMPPeQ+/fTTltPTH4qPgE/aVme+9KUvuUceecR98cUXmQAgws4Edj1UCAiBtBHwXVIycvI/p512Wtrq6Hk5QGDQoEE96olfZ84666zUcyDCTh1yPVAICIGsENhuu+1qNsAnnXRSVmrpuQEjsPnmm9esM2eccUaqmouwU4VbDxMCQiBLBPytO/5oyb7jXEUiBHwEVltttZqETb2ZN2+ef3tXv4uwuwqvEhcCQiAkBBZeeOG6jW8tn9Ih5UG6pIfA3Llz69YXCDvNYDIi7PTKXk8SAkIgYwR69+5dtwG+5557MtZQjw8NAZt9qXWs3ALaTf1F2N1EV2kLASEQFAKHHHJIXcL+xz/+EZS+UiZ7BPwdBtVIO00NRdhpoq1nCQEhkCkCkydPdnisqtbw/vSnP81UNz08TATM01m1OjNy5MhUlRZhpwq3HiYEhEDWCDz99NPOj9C0+OKLu2uuuSZrtfT8gBGYMGGC87d4sYe/MhpcGuqLsNNAWc8QAkIgOATwC034RIkQaBaB2bNnuxkzZjR7e+L3ibATh1QJCgEhIASEgBBIHgERdvKYKkUhIASEgBAQAokjIMJOHFIlKASEgBAQAkIgeQRE2MljqhSFgBAQAvMhQKQ4/E8rgMx80JTuBHVh/PjxPT6V4X6rgSLCroaKzgkBISAEWkCASG/WANciZCLEsTVIIVpbALZgt+JkZdttt626rZC6sfHGG7t6jlhE2AWrEMqOEBAC6SAASR900EE1G9/Bgwf3aHwtXCP/k5QPgQMPPDCuK/3793fHHXdc1HmjA8e1NddcM7per36IsMtXb5RjISAEOkTARsuMimhoIWMaXj7bbLONW2aZZaLG1x8tcY5rkvIhYGRNHaDu1BK/vlS7R4RdDRWdEwJCQAjUQICREUTdqPH1G2YaYv5zxx131EhVp4uKwKWXXhrXl1rLJc3mXYTdLFK6TwgIgdIjAOEaWbfS+ELyjMQl5UIAQ7I+ffpEdabR6LkZZETYzaCke4SAECg9AjS+ffv2jRpff/TcDDCQNSMtSbkQsNkYlkySEBF2EigqDSEgBAqPgE1ttroOjRER0+fNbNspPIgly6AZkiW1FCLCLlkFUnaFgBBoDwEse5kOb3V0DdFjdCQpFwIsmdjySVI5F2EnhaTSEQJCoLAIMEqm8eXTzki5nf8UFsySZMzsHWrNyFgH0OoVR6bQ64kIux46uiYEhIAQcC7aT02DWqvxpaHFIYb/0Zp1uasOW/yoM7XWr6lL9mHJhHsbTZ2LsMtdp5R7ISAEmkCg0fo1jW3lp9Wp8ybU0C05QsAIm2MjsbXuek5TSEOE3QhJXRcCQqD0CFjj28xatE11trLtq/QAFxAAqzONprlZLqGz18y2PxF2ASuKsiQEhECyCFjjW2t603+ajbT9c/pePgRsVgb/4PXE1rqbqlv1EtI1ISAEhIAQcJFlOETcqPE1j2a11rqFZXkQ8A0V6zlNsc4gx0aiEXYjhHRdCAiB0iPQbONro6pmGt/Sg1oCAOi40dHD21mtJRK7px6pG1QibENCRyEgBIRAHQSYsqTxxdtZrcbX7mlk7VvnMbpUIARYnzabBuoOuwiIic7n+OOPj2ZsOM+nGWnurmZS0j1CQAgIgQIjUNn4ElrTGl+OhNM0v9GNrH0LDJOyVoEA9YYZF9u6ZQRtR0bYzW4BFGFXgKufQkAICIFaCND4WqhEa3D9I5a+jayCa6Wt88VHgJkZpr751JqlqYeCCLseOromBISAEKiBgDW8dtSougZQOp0YAiLsxKBUQkJACAgBISAEuoeACLt72CplISAEhIAQEAKJISDCTgxKJSQEhIAQEAJCoHsIiLC7h61SFgJCQAgIASGQGAIi7MSgVEJCQAgIASEgBLqHgAi7e9gqZSEgBISAEBACiSEgwk4MSiUkBISAEBACQqB7CPw/L6sjhdAZ62IAAAAASUVORK5CYII=[/img][br][br]Triangle [math]G'H'I'[/math] is congruent to triangle [math]MNO[/math].
Triangle [math]GHI[/math] is similar to triangle [math]MNO[/math].
For each problem, draw 2 triangles that have the listed properties. Try to make them as different as possible: One angle is 45 degrees.
Draw 2 triangles that have the listed properties. Try to make them as different as possible: One angle is 45 degrees and another angle is 30 degrees.
Draw 2 triangles that have the listed properties. Try to make them as different as possible: One angle is 45 degrees and another angle is 30 degrees. The lengths of a pair of corresponding sides are 2 cm and 6 cm.
Compare your triangles with your neighbors’ triangles. Which ones seem to be similar no matter what?[br]
Prove your conjecture.[br]
[size=150]Here are 2 triangles. One triangle has a 60 degree angle and a 40 degree angle. The other triangle has a 40 degree angle and an 80 degree angle.[/size][br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAWoAAAFmCAYAAABEGtCYAAAgAElEQVR4Ae2dCRgNVf/HX0mbXimKilAoFbJG+lvaSGWNQnYlyYuSUtm1SVESUkghJUsSKaFFUhKKiIiyRFGoCOf/fM/7nmlcM/fOnTszd87M9zzPfe69M2f5nc+Z+d7fPXOWfwkGEiABEiCBUBP4V6ito3EkQAIkQAKCQs2LgARIgARCToBCHfIGonkkQAIkQKHmNZAWgXfeeUfGX7lyZVrpGJkESMA9AQq1e3axSzly5Ejxr3/9S1x44YXi+uuvj139WWESyBYBCnW2yGtW7gMPPCBFGkKtXpMmTdKsFjSXBPQkQKHWs90Cs/rw4cOiWbNmhjg/9NBDAi/lWQdmCAsigRgToFDHuPFTVf37778XV1xxhSHSL7zwgkxy8OBBcd5558njgwYNSpUNz5MACWRIgEKdIcCoJl+wYIE499xzpRifeeaZYt68eUdV9aWXXpLncuXKJTZv3nzUOX4hARLwlgCF2luekcht/PjxhhddsWJFsXbtWst61ahRQ8Zr37695XkeJAES8IYAhdobjpHJpX///oZIN27cWPz111+2dfvggw+MuAsXLrSNxxMkQAKZEaBQZ8YvUqnbtWtnCO8999zjqG5t27aVaWrVquUoPiORAAmkT4BCnT6zyKXYtm2buPrqqw2RfuaZZxzXcdOmTSJnzpwy7dixYx2nY0QSIAHnBCjUzllFMuaSJUtE8eLFpdCeeuqpYsaMGWnXc+DAgTJ9kSJFxKFDh9JOzwQkQALJCVCok/OJ9NkpU6YIjNrAmOhLLrlEfPXVV67rW6JECZlP7969XefBhCRAAtYEKNTWXCJ/dPDgwVJYIdJ169YVu3fvzqjOr776qpHfunXrMsqLiUmABI4mQKE+mkcsvnXu3NkQ1U6dOnlW59q1a8t8W7Ro4VmezIgESEBwPeo4XQR79uwRN954oyHSjz/+uKfVX7x4sZH33LlzPc2bmZFAnAnQo45J669YsUKULl1aCilGaUyePNmXmsNDR3dK1apVfcmfmZJAHAlQqGPQ6m+99ZbIkyePFNDzzz9fwPP1K2zfvl3kzp1bloVlURlIgAQyJ0ChzpxhqHMYPny4FE14uZiUsnXrVt/tVQ8qCxYsKPbt2+d7eSyABKJOgEId4Rbu0aOHIdJt2rQJtKaqm+W+++4LtFwWRgJRJEChjmCrHjhwQDRp0sQQ6b59+wZey6lTpxrlr1q1KvDyWSAJRIkAhTpKrSmEwBjmypUrGyKZzWnd9evXl3ZgcScGEiAB9wQo1O7ZhS7le++9JwoUKCDF8eyzzxbz58/Pqo1ffvml8YMxc+bMrNrCwklAZwIUap1bz2T7iy++aIhilSpVxPr1601ns/exW7du0q7y5ctnzwiWTAKaE6BQa96AMB/ra2BUB1633HJLqBZGwtT0fPnySduGDh0aAdqsAgkET4BCHTxzT0ts1aqVIdI9e/b0NG+vMnv22WeljXnz5hW//PKLV9kyHxKIDQEKtaZNvWXLFqG2woInPWLEiFDXBFt6wc4uXbqE2k4aRwJhJEChDmOrpLDp448/FkWLFjW81LfffjtFiuyfho2qe+bzzz8PxKDly5eLfv36iZo1axovfN+4cWMg5bMQEvCKAIXaK5IB5TNx4kSRI0cOKXply5YVOo1Rbtq0qbQbC0P5GSDQEGf1w2D1Pm7cOD9NYN4k4CkBCrWnOP3N7NFHHzXEp169euL333/3t0CPc//mm28M+7FpgV8BDy0hzl27dhUQbXNQ53B+wYIF5lP8TAKhJUChDm3THG1Yx44dDZHTuZ/3gQcekPW4+OKLj66gx9+SdW9AwCHU2Zix6XE1mV1MCFCoQ97Qu3btEnXq1DFEesiQISG3OLl5f/75pzjnnHNkfR577LHkkX06i24PCDVmTjKQgA4EKNRptpL662zljU2fPl0KAPqOM93aCmYtW7ZMlCpVSuZ54oknijfeeCNNa8MZ/YUXXpB1Oumkk8RPP/0UuJFoO3rUgWNngRkQoFCnCQ8CfNppp8lRF+ak6AvFOGGcS+wXNcdz+nnatGnilFNOkYJSsmRJsXTpUqdJtYh35ZVXyrrdcccdgdqr2glCnax7JFCjWBgJpCBAoU4ByOq06uNUIwcg3pdddpkUHi9EWnntEJNrr71W7Nixw8oMrY9hXRLUD6+PPvrIl7qgXRYuXGi8MDRP/ZiqtvOlYGZKAh4ToFC7AApPDAKDIWAIapU4L25+tTYG8u/QoYML6/RJomZVXnPNNb4YjVEd6sdAvTdo0ICetC+0mamfBCjULum2bt1aigBufIgAvOxMwv79+0XDhg0NYRk4cGAm2WmRdsOGDUZ9X375Zc9txg8q+qPxQnuZZ3LiB9GL5wieG80MScCCAIXaAoqTQ2ZvLdPRA6tXrxZYXU55fRMmTHBiQiTioDsC9cZejkEEiDce9nrx4xqEvSyDBECAQu3yOjALNUZ7uA1z5swxVpcrXLiwWLRokdustE0HkYZwQrSDCPCk1Y9iEOWxDBLIlACF2gVBNXIAIzxww+NvtZswatQoQzAwCmLTpk1ustE+Dbo9wBFT49EdEkRQXrUXD3+DsJdlxJsAhTrN9lcjPNQwPNXvme5Qr169ehki3aJFizStiF50PFCEWOMBYxBBedTptlsQtrEMEkgkQKFOJJLiuxJmNcID7+l41UeOHBHNmzc3RPrBBx9MUWI8TmOInhLP999/39dKqzYrUqSIr+UwcxLwigCFOg2SaqRH4ggP3PAYn5tqFAG8t2rVqhmCNHr06DRKj35UTH6BWKMbKJOA9sCoDoyhNgd0c6ix1Cgnk2cL5nz5mQT8JkChdkhYeWHwqBODkynJEI1ChQpJIcqfP7+YO3duYjax/47p5JhWDhHFNHO3QT07UB564jvOU6Td0mW6bBCgUDugDk8MAo1heFZeM47hvN1DRfWwDIJRoUIFsWbNGgelxjMKFmoCp3PPPVdgASe3AUJsHj+NtsN31WXlNl+mI4FsEKBQ+0x9wIABUnggPo0aNRJ//PGHzyXqnz2WQAUvLInKQAIkwHHUvl4D7du3N0S6e/fuvpYVpcyxqQCEGi9MBmIggbgToEftwxWwfft2oYabQWyGDRvmQynRzvKGG26QQo3tuxhIIO4EKNQeXwGfffaZKFGihBSZ3Llz86GVS77YAFd51Tps3uuymkxGAo4IUKgdYXIW6fXXXxcnnHCCFBj0s3755ZfOEjKWJQFsOQaxrlSpkuV5HiSBuBCgUHvU0k8++aThAV5//fXil19+8Sjn+GaDbcgwPh1i/eyzz8YXBGseewIUag8ugbvvvtsQ6TvvvNODHJmFIqA2UciXL5/Ys2ePOsx3EogVAQp1Bs3922+/iZtuuskQ6Wxt1ppBFbRIWq5cOckYsw0ZSCCOBCjULlt95cqVokyZMlJAjjvuODFp0iSXOTFZKgIzZ840fgzZ75+KFs9HkQCF2kWrzpo1S25ii77TYsWKiU8++cRFLkySDoHGjRtLsc50k4Z0ymRcEggLAQp1mi3x3HPPGd4d9kz88ccf08yB0d0QwD8YNVxv6tSpbrJgGhLQlgCFOo2mu++++wyxsFvXI43sGDVNAop/6dKl00zJ6CSgNwEKtYP2O3jwoMAMOeXR9enTx0EqRvGawL59+0SBAgVkOwwePNjr7JkfCYSWAIU6RdN899134vLLLzdE+qWXXkqRgqf9JDBy5EjZFpj1ian6DCQQBwIU6iStjJ1GChYsKIUB737vPJLEFJ4yEahatapsk06dOpmO8iMJRJcAhdqmbeE5q64OeNTwrBnCQQCbLqi2Wbx4cTiMohUk4CMBCrUFXPRBKyFA3zT6qBnCRQAbAqONateuHS7DaA0J+ECAQp0AVe2LCBHAKAOGcBJYt26d8WM6ceLEcBpJq0jAIwIU6v+BxHhojItWnjTGSzOEm0Dv3r1le2FZWQYSiDIBCrUQcmYhZhhCpLHxKWYeMoSfwKFDhwR2HEe7DRw4MPwG00IScEkg9kKNNTqwVgdudqzdgRlwDPoQGDt2rGy7448/XmzatEkfw2kpCaRBINZCrXa8hkhjFTyshsegH4FatWpJsW7btq1+xtNiEnBAILZCjXWjIdB4YT1pBn0JLFy40GjLBQsW6FsRWk4CNgRiJ9TYeQU7sCiRxs4sDPoTaNeunWzTGjVq6F8Z1oAEEgjESqixljH2MoRIY29D7HHIEA0CmzdvFrly5ZJty2n+0WhT1uIfArER6unTpwusDwGRxnAu7BbOEC0CgwYNku173nnncZJStJo29rWJhVAPGzZM3sAQ6WuuuYaL+UT4sr/wwgtlWz/00EMRriWrFjcCkRfq7t27GyLdvn37uLVv7OqL4Zbq+cPatWtjV39WOJoEIivUf/zxh2jUqJFx0w4YMCCaLchaHUOgTp06st2bNWt2zDkeIAEdCURSqNesWSMqVKhgiPTLL7+sY9vQZpcElixZYrT9nDlzXObCZCQQHgKRE2osgZk/f355oxYqVEhgjC1D/Ajcdddd8hqoUqVK/CrPGkeOQKSEevTo0YYnVa1aNbFx48bINRgr5IzAjh07xL///W95PYwYMcJZIsYigZASiIxQP/jgg4ZIN2/eXBw5ciSkyGlWUASGDBkir4mzzjpL7N27N6hiWQ4JeE4gEkKtFpHH0/5evXp5DokZ6ksAC23huujRo4e+laDlsSegtVBjtbQrr7zS8KRHjRoV+wYlgKMJTJs2zbg+VqxYcfRJfiMBTQhoK9SLFi0ShQsXljdhvnz5BJ/ua3LFZcHMBg0ayOsEwzUZSEBHAloK9YQJEwwvqXz58mL16tU6sqfNARHA8Ew1CQZLCTCQgG4EtBNq7OShbrqGDRuK/fv368ac9gZI4OmnnxbVq1cXyqu+7LLLAiydRZGANwS0EuoOHToYIt2tW7eUBLA2capx1PCw+vXrJ1/Lly+3zXP37t0yDvZVRHwO/fsvKjDGWipgMn78eFt+4IXzKh542gXkifaFuCJvN2Hnzp0C1wuWEPj111/lphBqfD3Em4EEdCKghVBjTOy1115riPTQoUNTMu7bt68R3yoyRLlo0aJGHOWlQxwSRQTfsTcfRB2f8Y51j5MJu1WZUTkGBhBcxcz8blXHcePGWcbF8cSAY/Xr15dsIe5o63TXmMYaH1hzPHGD4uHDh0s78uTJIyDkDCSgC4HQC/XSpUtFyZIl5Q12yimnCDzFTxUgoBCPsmXLyvfE+BAaiDQ2soUQ4DteStwh1ubQunVrkbhzCEQEghLHoLiCi/nHyupfBn7UVFuouHhXeeC8OeB4YkC7WIl6Yjx8x/MKdHW89tprVqdF5cqVpT3c1ccSDw+GlECohfqNN94QJ554oryxSpUqJZYtW5YSIwQX/ZDwwvCCSCQGiDOOW3nmEB+cU6KCtHYenZWoJJYVte/qx8yKnVVd8U8EP4hoF3PAdxxHV5IK+DHs2rWr+mq84zjKTRV+/PFHuYxtsg0hZs+eLdsXbcw1yVMR5fmwEDhWxUJimZpVhhsKq6Ht2rXLkWW40ZXQ2gm1Op4oHigAAo30ZsFAfKu4cRNqMMibN6/0hp00BjxssMSPn1VQP4rKE7f7lwKv24lQY7W8F1980aqoo47deuut0q66desedZxfSCCsBEIp1F26dJE3Em5yDL/r37+/I37wvJBGeXtKkBMTI04ykcV5pFUBQpEoNijDiXioPKLwrvqanXZDqG4P1R6JDKzyA3fzvxn8OOCYEvPEPNR3tEWfPn3U16TvWF0RbYyXXRdJ0gx4kgQCJhAqof79999FvXr1jJvo0UcfFYcPH5bH3n777aRolLdnFlh8xs1oDoiXKMTm8/iMv+vwHM0BYgNxb9OmjexaiZtIgwXqDHZKSPHDiJEcM2bMsBRSFR/xrIL6YTWzRPug7x9dImAN5nbpVZ6zZs2SI0TSWd8FSw2gLhdddJHKhu8kEFoCR6tYFs1ctWqVvClx8+TIkUNMnDjRsGbx4sXyxsVmAHYBNzf6PM2el5VQK3Ewd20k5mmVTsVRIqW+x+ldcQEDqxEziUMm3Qi14gnBNrelOp74jmsCdn366aeJp5J+P3DggMAyuLje4BAwkECYCYRCqOEtw4PFTQMB+Pjjj49hhu6PwYMHH3McB9Rf6MQRBEpYzImUUJu9OPN5fLZKlxgnjt8VF7QV+CkhhXDjhxLtZ+7mcCrUyNdtePLJJx13jSWWMWbMGGkzHlhv2bIl8TS/k0BoCGRdqLFWMG5wvHDD2t0wGPeKldASz0MsIByJfcggrITFTFsJtVuP2pxX3D4rnmYxNjNI7DJyKtTJfjTN+Sd+xrVQunRp8fPPPyeecvwdQ/lw7WFyDAMJhJVAVoW6Z8+ehki3atUqJSPMKEv8mwrxgEDgr3JiUMKSeFz9KCQeV9/VkDL1ne//JWDHU/FRI26Up+23UD/22GPiqaeeUsW7ep8/f75xDX744Yeu8mAiEvCbQFaE+tChQ+KWW24xbpDevXs7que2bdvkgzzVV628Y+WRp3pHfATES7bmQyohd2RsBCOp7g27qiUKs9NRH3Yeul05OI5rAG24devWZNEcnVPDBK+++mpH8RmJBIImELhQr1+/XmAfOyWqTsa9mqFg7YYpU6bIQ+gbhZdn98LDRSW6iKMeBCrBsfLClfgn6xox2xOnzxBU8FQ/eIl1V1yVRw2+iG/VLYW0SiBVuyTml+w7rgFcC14E2HvcccdJW5OtV+JFWcyDBNwQCFSo8Tfz7LPPljdEgQIFxHvvvZe2ze+++67j/kS7v+rq4aOVJ6fExk6M0jY4QgkgaBBe82xCVT2IMp4VoNvIHFQbKPFW5+ziq/Op3tu3by/mzZuXKprj83hYjboVK1ZMDgl1nJARSSAAAoEJ9dixY+WNgJsB6y2sW7fOVfUOHjwoHyDt27cvZXolElYRMT4XtmB1NogIXhhehmNIx2BNQHVvYD0UeMIQXIyjRjcE2CWOvEEcHMd5xENAHLv41qUefRTj7fFg+e+//z76RIbfihcvLm11OnEmw+KYnAQcEwhEqNXNjRu2SZMmAmNYMwnwppx4vMmEGgKjxBp2qRfS4ByDPQFzeypu6Gay+oeCXPAPRnVDqfh4x3E3Af/Mbr/9djdJk6Z55ZVXjOsAXXQMJBAWAr4LNWaXqZvTqw1GsVzlM888k5IhvLlUgo44EBi88JnBGQH8A4HQQrThIaf6ccN5xHMaP5kVaCsM6/QjqOV0W7Zs6Uf2zJMEXBHwTajxNL5WrVqGSENcvQrom+zcubNX2TEfzQh06tRJwKv2I3zyySfGNetlH7gftjLP+BDwRagx5fv888+XFzwWaX/rrbc8JYr+7RtvvNHTPJmZPgSw6p2fXRMdO3aU1261atX0gUJLI03Ac6GePHmyyJkzp7zQMWtsxYoVngPcu3evqFixouf5MkM9CFSoUEE4eZjstjb4N4hNKtBlN2rUKLfZMB0JeEbAU6F+5JFH5MWNCxxbIeGCxw3lx+vSSy+V/aJ+5M08/WkzL7iirxtt70VeyfJQmygXLFhQTq7x7I5jRiTggoBnQo3uiJNPPtkQavUAke//jCghCz1Z4AEoAwlkk4BnQo1KwIumGOkpRmw363a7+eabs3l/smwSkAQ8FWqsv7Bnzx6+yCAy14BaV4Z6QQLZJOCpUGezIiybBEiABKJKgEId1ZZlvUiABCJDgEIdmaZkRUiABKJKgEId1ZZlvUiABCJDgEIdmaZkRUiABKJKgEId1ZZlvUiABCJDgEIdmaZkRUiABKJKgEKtWctiCjU2O8AuK3hhVxW8c4lWzRqS5pJAGgQo1GnAynZUrP8MYcYsQizEj00O8MIGCKnW3c627SyfBEjAPQEKtXt2gaaESCuBTtzuKlBDWBgJkEDgBCjUgSNPv0DspgJPGl40PjOQAAnEiwCFWoP27tq1q/Sm3e4xqEEVaSIJkEASAhTqJHDCcqpIkSJSqFPtSxgWe2kHCZCAtwQo1N7y9Dw3dHWgbxoPDVXACI+FCxfKlzrGdxIggegSoFCHvG0xmgNC3bp1azkEr2jRovI7juGFvut+/fqFvBY0jwRIIBMCFOpM6AWQFiM8IMgNGjSQoly/fn2BYxBw7DyCB4w436ZNmwCsYREkQALZIEChzgb1NMqEGCvv2ephIvqtlVhzREgaYBmVBDQiQKEOeWMpoTb3USearEaFDB06NPEUv5MACUSAAIU65I2ouj6SbbDqJE7Iq0nzSIAEkhCgUCeBE4ZTGOGBrg88TLQLatZiMjG3S8vjJEAC4SdAoQ5/G8k+aIzusAvs+rAjw+MkEA0CFGoN2lH1U1t5zHiYqBZq4sNEDRqTJpKACwIUahfQgk4CMcYKeWoYHia7QJRnzJgh1LhqeNUMJEAC0SRAodakXSHWGPmhhuqZ3ynSmjQizSQBlwQo1C7BZSsZHi6iCwQvDMdjd0e2WoLlkkBwBCjUwbFmSSRAAiTgigCF2hU2JiIBEiCB4AhQqINjzZJIgARIwBUBCrUrbExEAiRAAsERoFAHx5olkQAJkIArAhRqV9iYiARIgASCI0ChDo41SyIBEiABVwQo1K6wMREJkAAJBEeAQh0ca5ZEAiRAAq4IUKhdYWMiEiABEgiOAIU6ONYsiQRIgARcEaBQu8LGRCRAAiQQHAEKdXCsWRIJkAAJuCJAoXaFjYlIwD2Be++9V9x8882iadOm7jNhylgRoFDHqrlZ2WwS+Ouvv6RAm9cSHzRoUDZNYtmaEKBQa9JQNFNvAmvXrhWVKlUyNn5o27at/JwrVy6xefNmvStH630nQKH2HTELiDuBefPmibPOOksK89lnny0++OADiaR69eryWPv27eOOiPVPQYBCnQIQT5NAJgTGjBljeNFVqlQRGzZsMLKDYKtuEOyDyUACdgQo1HZkeJwEMiTw8MMPG0J8yy23iEOHDh2TY5s2bWScWrVqHXOOB0hAEaBQKxJ8JwEPCbRs2dIQ6Z49e9rmvGnTJpEzZ04Zd9y4cbbxeCLeBCjU8W5/1t5jAngwqPqe0a0xYsSIlCUMGDBACnWRIkUsve6UGTBC5AlQqCPfxKxgUAQ++ugjAbGFQOfNm1fMnj3bcdHFixeX6Xr37u04DSPGhwCFOj5tzZr6SODVV1+VQguRLlu2rPj666/TKs2cft26dWmlZeToE6BQR7+NWUOfCTzyyCOGSNerV0/s3bvXVYnXXXedzKdFixau0jNRdAlQqKPbtqxZAATuuOMOQ6S7dOmSUYmLFy828nr33XczyouJo0WAQh2t9mRtAiKwc+dOUbt2bUNYhwwZ4knJd955p8yzatWqnuTHTKJBgEIdjXZkLQIk8MUXX4iLLrpICuqJJ54opk6d6lnp27dvF6eccorMe+TIkZ7ly4z0JkCh1rv9aH3ABN58801x8sknSyEtWbKk+Pzzzz23YPDgwTL/ggULin379nmePzPUjwCFWr82o8VZIvD0009LAcXIjmuvvVb8/PPPvlly6aWXyrLuu+8+38pgxvoQoFDr01a0NIsEunbtaoh0hw4dfLcE3Sn4QcBr1apVvpfHAsJNgEId7vahdVkmgK6HBg0aGKI5cODAwCzCUD8IdePGjQMrkwWFkwCFOpztQqtCQOCbb74R5cqVM0T6lVdeCdSqL7/80ih75syZgZbNwsJFgEIdrvagNSEh8M4774gzzjhDCmXhwoXFhx9+mBXLunXrJm0oX758VspnoeEgQKEORzvQihARwLA41T985ZVXih9++CFr1u3evdv4wRg6dGjW7GDB2SVAoc4uf5YeMgIPPPCAIdJhmcr97LPPSpuw0NMvv/wSMmI0JwgCFOogKLOM0BM4fPiwaNasmSHSDz74YKhsrlixorQt02nqoaoUjXFMgELtGBUjRpXA999/L6644gpDpEePHh26qs6aNcuwz49JNqGrMA06igCF+igc/BI3AgsWLBDnnnuuFMH8+fOLMC+G1LRpU2nnjTfeGLdmin19KdSxvwTiC2D8+PGGl1qhQgXx7bffhhoGhguqh5xTpkwJta00zlsCFGpveTI3TQj079/fEL1GjRqJP//8UwvL1cPOiy++WAt7aaQ3BCjU3nBkLhoRaNeunSHS3bt318hyIX9QzjnnHGn/Y489ppXtNNY9AQq1e3ZMqRmBbdu2iauvvtoQ6WHDhmlWg/+ai4ed6AI56aSTxE8//aRlHWh0egQo1OnxYmxNCSxZskSoDWRz584tZsyYoWlN/ms2JuJArLHDDEP0CVCoo9/Gsa8hHrzlypVLChsW5ccEEt3De++9Z/wzwO7nDNEmQKGOdvvGvnZqEX54n9dff7344IMPROnSpbO2doeXDdKyZUsp1tdcc42X2TKvEBKgUIewUWiSNwQ6d+5seJ3Yi1AFiHWZMmXEp59+qg5p+b5hwwajfhMmTNCyDjTaGQEKtTNOjKURgT179ghMClFjjq1GR8ybN0+ULVtW6N5t0LdvX1nP888/X6MWoqnpEqBQp0uM8UNNYMWKFbJrAyJ93HHHicmTJ9vaC88aW17Nnj3bNo4OJyDSqG+/fv10MJc2uiBAoXYBjUnCSeCtt94SefLkkaJVrFgxsXjx4pSGYt2M6tWri7Fjx6aMG9YIL7/8svHvAd0hDNEjQKGOXpvGskbDhw83xKpmzZppjS/GetPNmzcXvXv31padGh/eqlUrbetAw+0JUKjt2fCMJgR69OhhiHTr1q1dW43+XkwnX758ues8spUQfe2qT/7999/Plhks1ycCFGqfwDJb/wkcOHBANGnSxBCoPn36ZFzotGnTBNZ+HjFiRMZ5BZ3B7bffLllgMgxDtAhQqKPVnrGpzbp160TlypUNkfayj3nr1q3innvuEQ0bNpTjrnWBiunkJ5xwgmTywgsv6GI27XRAgELtABKjhIsAZuUVKFBAClLBggXF/B8SxnIAAB4oSURBVPnzfTEQa1PXq1dPYDz2smXLfCnDq0wPHjwosNejWrAJ77qsCOgVgyjnQ6GOcutGsG4vvvii4UVffvnlYv369b7XcuLEiQKz/yDYH3/8se/lpVMANr+FQGOHml69ekkepUqVkoywJCpDNAhQqKPRjrGoBUZlqAdm2O3k77//DrTeWDMEDxvxwpC4nTt3Blq+ubAvv/xS4OHnJZdcItA3v3btWuM07FScVq9ebRznB30JUKj1bbtYWY5hZ0p87rvvvqzWHeOz4b1edtllcvW6SZMmic2bN/tuE3Z4wUPOBg0ayJmXWO7U7sfihhtukLzwg8agPwEKtf5tGOkabNmyRdSoUcMQ6TCNxoBHP3fuXCnamDRTt25d8fDDD4s33nhDfP311wL9xpmENWvWyLzwo4Bx0lhU6oknnhBffPFFymwxkUf9sL399tsp4zNCuAlQqMPdPrG2Dv3BRYsWlYJz2mmnibALDoQV3jWEFV4vuiXq1KkjOnToICfTYKOCcePGiddff12uhz1z5kzx5ptvildffVU8//zzYuDAgbIfHA8wMbX9pptuEuhnfu2114SbGYddunSR7CpVqhTr6ygKladQR6EVI1gHPMDLkSOHFBqsdLdq1SrtannkyBHx/fffyyVVIc546Pf444/LPmUI8P333y8eeughMWjQILlGNgQbk1WwyS7GiGcafvnlF4EfOHjWUViDO1MeOqenUOvcehG1/dFHH5XiAoGBV/n7779HtKb+V2vo0KGSZb58+QRWFWTQkwCFWs92i6zVHTt2NET67rvvjmw9g6xYuXLlJNNu3boFWSzL8pAAhdpDmMzKPYFdu3bJ/lz1AOzJJ590nxlTHkUAfeGKK4b1MehHgEKtX5tFzmLM+lOTNDAFGqMmGLwl0LhxYynW9evX9zZj5hYIAQp1IJhZiB0BLIKEDWfh8ZUoUUIsXbrULiqPZ0Bg5cqVhlc9derUDHJi0mwQoFBngzrLlATUgy6INKZo79ixg2R8JICJQmCNzX0Z9CJAodarvSJjLR5sqX7T9u3bR6ZeYa7Ivn37jMWssDs7gz4EKNT6tFUkLN2/f79cPlSJ9IABAyJRL10qgbHcYJ87d26xfft2XcyOvZ0U6thfAsEBwAJB5cuXNzzpCRMmBFc4SzIIVK1aVbZBp06djGP8EG4CFOpwt09krJszZ47ApAt4c4UKFRKLFi2KTN10qwjWJ1H/aJxsAKxb/aJoL4U6iq0asjqNGjXKEIZq1aqJTZs2hczCcJizYMGCwAxp0aKFbJPatWsHViYLck+AQu2eHVM6IIAFipT3hp2+dQwbN24Ubdq0kcuaoi5Y3hTfcdwuTJ8+3YiPNFikyW7TXIx+wQqBXbt2FWXLlhVBzCDEVmaqXbCuCkO4CVCow90+GVsHMUkmKBkXYJMBFiSCMCsxgGDrGCCuefPmlYsbQUixWD/e1WJHVl4wzqPeRYoUkXHN8SHg5oDviTunQ7hRjt8BS7LCToxfZwg3AQp1uNvHlXXKA1Qiqd5r1qwprITFVSFJEqF8dHGocrHAva4BHi5EOdEbxncch3dtDqg76o102CZLBXyGcEP0zcfhSZu/q/g47nc4dOiQtAn2YolVvwN+lNQ1Yffutw265k+h1rXlbOxWHiBuBEwXhmeGF7w2dXMkenU2Wbk6vHDhQvmwEGXh4SEeXOkcUA870cRxnDcHxdnqBxFrUSM+3lVIlreK4+c7dm+HTTlz5vT92QGuQ5SFHzHU2+rlZ111zvvoq0znmtB2SQDijJsBf58Tg/JosBi/HwH7CKJsvDAMDwvp6x5Ql0SvWdUJgoPz5gCvGZ62VYDnjPjm9TYg7ImiDq/cHMcqLy+P4Z8W7Grbtq2X2R6TlxLqxPoeE5EHjiFw9FV2zGke0I2A6ju1sxtCkigudnHTOY6JK8gXr4YNG4o//vgjneShjas8ZLMXDGOVd4z+Z3NA/e28ZMRD+5h/KCHeEPzx48fLLhD8mCJ9YleLuQyvP+NfkGo7P0VU9d37WYbXbMKSH4U6LC3hkR1WXp4561RCbo7r9DOmgKsbPYgRC07t8iKeElLUDyM9IGp4x3eIuDkojzmZUOMc0poD0uEfELxoeJ3wqIMO7dq1k3Ylsz1Tm1TdUV+G9AgcfcWkl5axQ0hAeYC44ROD6vpIFJjEeE6/YwoyFlNSIo09AaMaIKKqnnhP9KRRb3iKducUFyVW6ntY3rGL+vHHHy/tf+mll3wxK6x196WyHmdKofYYaLazg7eiujfg3SrvBR4bRAQetzqWia2fffaZHNaFPLFMqZ8PKDOxM9O0YIUx0KgnhMY81A7HzSx1Fmpwwt6NqGfhwoUz3kHdirsSanTr4J+JemXjH4SVfWE+RqEOc+u4tA0XvropMBxM7eQNT9osLC6zl7toY4F/3NRY8D/Ku4Yojol91Kq/1fygEWyVoNuxVfnZnc/28ZIlS8o6YNNdrwPY2L3wQDPIfnmv6+Z3fhRqvwlnIX8IRr9+/Y65KcwetluzsEWWutnq1KkjsNN1VIN6YGjVjYQ6K7E2i3gqocYzAvzjCWuYNGmS0b5r16711Ez84wBL/LvDZ/wLw3f1XAXsKNbWyCnU1ly0PQpvGl4eLnoICURbjSTAMXjYbm8GbDaLPPDCJrRRDxAR1BWiYhVUV4dZyCE6YGwVlMcd5NA7KztSHcMPMOrdrFmzVFE9O69Ym0fEeJZ5BDKiUEegEc1VUP3TZi9PnVf91Imz49R5u/fffvtN3HTTTYZIP/roo3ZRI3VciUc6Qq28bKs0ykNHO4Q5LFmyxGhrrHoYVFAjktw6EkHZmY1yKNTZoO5TmcrDSzaqQ40KcSoW2GuvTJky8sbNkSOHwF/juAQIBjxL/EOBN2wO+K7+uZiFBf9orNIgPrxFiFFiXuZ8w/L5rrvukvW4/PLLAzNJ9d9b/cgFZkRIC6JQh7Rh3JilPEDzX/HEfNQQPXh+qcKsWbOksEB4IDKffPJJqiSRO69+2PAvBH386PvHO76DixVH5TmDGeJi3LWKb/VPJ4zQfv75Z3HqqafKOo4YMSIQEynU9pgp1PZstDujujasxENVRsVJJuaI+9xzz8mbFGKEG+jHH39UWcTuHT9u6FdWf83RD43vyTw/cxqkSxU/jFCHDBkir4GzzjpL7N2711cT8S8D1xpeDMcSIJVjmWh7RP1Vh/dmNTZV/f3GzZBMZNRu1YjXqlUrbXnQ8MwJqG6ve++9N6PMcD1aXZPIFNelGquerNsuIwM0T0yh1rwBE81XD7PUX3WsIYGX+e+63c1w8OBB0bRpU8Oz6d27d2L2/B4zAtOmTTOuhxUrVriuvXp+gvHS6D5SL/N16dVkLNdGhjghhTrEjePWNPSDqtEf6u8k3nHM7iHid999J/DgSMX3axqx2zoxXfYIKG+3UaNGro2AN43uH3V9md/RNZSqK851wRFJSKGOSENaVQM3BzwZvOz+diLd+++/LwoWLChvogIFCsjvVvnxWDwJfPXVV4bAou8904AuOifXZablRCk9hTpKremiLvCclXdTuXJlAc+agQQSCdxzzz3yOjFPmU+Mw+/+EaBQ+8c29Dn36dPHEOkmTZr4shBP6CHQQEcEMOkpf/788np56qmnHKVhJO8IUKi9Y6lVTmp8MLzpHj16aGU7jc0OATVkM0+ePGLnzp3ZMSKmpVKoY9bwGA+ttl6CSOPmYyABpwTQPYbrBuu+MARHgEIdHOusl4SZhcWKFZM3Gp60Y+YhAwmkQ2D27NlGdxnWJGcIhgCFOhjOWS8Fa3Qcd9xx8ibDJAas4cFAAm4I3HrrrfI6qlu3rpvkTOOCAIXaBTTdkjz22GOGF4RV8PBgiIEE3BLA7vJqpNDkyZPdZsN0aRCgUKcBS8eod955p3FTde7cWccq0OYQEnjwwQfldXXRRReF0LromUShjl6byhph55Xrr7/eEGnszMJAAl4ROHDggChUqJC8vuKyPrlX7NzkQ6F2Qy3kabCH4cUXXyxvIuxt+Prrr4fcYpqnI4ExY8YY19iWLVt0rII2NlOotWkqZ4Ziim/u3LnlDVSiRAnBJ/POuDGWOwLVq1eX11qHDh3cZcBUjghQqB1h0iPSsGHD5E2DBz3XXHON2L59ux6G00ptCcyfP9+45j788ENt6xF2wynUYW8hh/Z1797duGHat2/vMBWjkUDmBNQs16uuuirzzJiDJQEKtSUWfQ7+8ccfAstPquFSAwYM0Md4WhoJAliZUY3Rx9rnDN4ToFB7zzSwHDGetUKFCoZIv/zyy4GVzYJIwEygf//+8jrEPpGHDx82n+JnDwhQqD2AmI0s5s6da6xmhmFSCxcuzIYZLJMEDAIXXHCBFGusysjgLQEKtbc8A8lt9OjRhhddrVq1pJsCBGIQCyEBIcQrr7xiXJfr168nEw8JUKg9hBlEVmpGGPqkmzdvLo4cORJEsSyDBBwRuPbaa6VY33bbbY7iM5IzAhRqZ5xCEatFixaGx9KrV69Q2EQjSMBMACs0qgfb8+bNM5/i5wwIUKgzgBdU0k2bNokrr7zSuAFGjRoVVNEshwTSJtCxY0d5rV5xxRVpp2UCawIUamsuoTm6aNEiUbhwYXnh58uXT8yZMyc0ttEQErAisG3bNnHyySfLa5ZOhRWh9I9RqNNnFliKCRMmGF50+fLlxerVqwMrmwWRQCYEnnjiCXntnn322QJj/RkyI0Chzoyfb6kHDhxoiHTDhg3F/v37fSuLGZOAHwQuueQSeQ337NnTj+xjlSeFOoTNjQVu1AOZbt26hdBCmkQCqQm88cYbxnX89ddfp07AGLYEKNS2aII/sWPHDqGGN0Gohw4dGrwRLJEEPCSAHYVwLd98880e5hq/rCjUIWnzpUuXipIlS8qL+pRTThHTpk0LiWU0gwTcE1i2bJnhVb/11lvuM4p5Sgp1CC4A/EU88cQT5QVdqlQpgYubgQSiQqBr167y2sa6NAzuCFCo3XHzLNWQIUMMj6NOnTpi165dnuXNjEggDAR2794tTj/9dHmdY810hvQJUKjTZ+ZZii5duhgijUkCDCQQVQLPPPOMvNYh2L/++mtUq+lbvSjUvqG1z/j3338X9erVM0Sam4Pas+KZ6BBQS/KiK4QhPQIU6vR4ZRx71apVomzZslKkc+TIISZOnJhxnsyABHQgMGvWLMM5+eKLL3QwOTQ2UqgDbIq3335b5M2bV16sWGD9448/DrB0FkUC2SfQpEkTef1j2B6DcwIUauesMoo5YsQIw5uoUaOG2LJlS0b5MTEJ6EgAE1/UZC6MdmJwRoBC7YxTRrEwhVZdnK1atcooLyYmAd0J3H///fJ+wBRzBmcEKNTOOLmK9ffff4tbbrnFEOnevXu7yoeJSCBKBLBIExZrgvOCxZsYUhOgUKdm5CoGtiKqUqWKIdIvvviiq3yYiASiSADLn0KosRzq1q1bo1hFT+tEofYU538zmz9/vuExFChQQLz33ns+lMIsSUBvAtjvE2LNOQSp25FCnZpRWjHGjh1reNGVK1cW69atSys9I5NAXAhgqy717AZbeDHYE6BQ27NJ+0zfvn2NCw/DkA4cOJB2HkxAAnEi0LJlS3nPYNVIBnsCFGp7NmmdadOmjSHSPXr0SCstI5NAXAngWY7yql955ZW4YkhZbwp1SkTJI/z000+iVq1axsU2fPjw5Al4lgRI4CgCffr0kffPBRdccNRxfvmHAIX6HxZpf1q8eLE4//zz5UWWJ08ewfV200bIBCQgjhw5IooVKybvo/79+5OIBQEKtQUUJ4cmT54scubMKS+u0qVLixUrVjhJxjgkQAIWBMaPHy/vJax/s3HjRosY8T5EoXbR/o8//ri8qNC3duONN4o9e/a4yIVJSIAEzASuuuoqeV+1bt3afJifhRAU6jQvg06dOhki3blz5zRTMzoJkIAdgQ8//NC4tzAXgeEfAhTqf1gk/YTFzuvWrWtcSIMHD04anydJgATSJ9ChQwd5j/3f//1f+okjnIJC7aBxly9fLrCADLo6cuXKJaZMmeIgFaOQAAmkS+DHH38UJ5xwgrzXxowZk27yyManUKdo2hkzZohTTz1VXjjFixcXS5YsSZGCp0mABDIhgB2P4BSde+65nDT2P5AU6iRXlNrnDRfN1VdfLbZt25YkNk+RAAl4ReCiiy6SYt2rVy+vstQ6Hwq1TfPdc8898kKBSLdr184mFg+TAAn4QeC1114z7r81a9b4UYRWeVKoE5rrzz//FI0bNzYuEg7ATwDEryQQEAH18B5rusc9UKhNV8C3334rKlasaIg0BuEzkAAJZIfA0qVLjXtx9uzZ2TEiJKVSqP/XEO+++64488wz5YWBhxgLFiwISRPRDBKIL4G7775b3pNYMjjOgUIthHjhhReMX+4rrrhCfP/993G+Jlh3EggNgV27dgmso4NnRXFe8Cz2Qv3QQw8ZIt2sWTNx+PDh0FykNIQESECIp59+Wt6j+fPnF7/99lsskcRaqG+77TZDpB944IFYXgCsNAnoQOCyyy6T92r37t11MNdzG2Mp1D/88IPAFFX8ncJr5MiRnoNlhiRAAt4RwMQzdb9ipnDcQuyEGgu/nHfeebLRzzjjDPHOO+/Erc1ZXxLQkkCjRo3kfdugQQMt7c/E6FgJNbb6Ub/K5cqVE998800m7JiWBEggQAIrV6407t8333wzwJKzX1RshHrQoEFGI+MXed++fdmnTwtIgATSIoD9SOFslSlTJq10ukeOhVDffvvthkh37dpV9zaj/SQQWwJ79+4VZ511lryfhwwZEhsOkRbqn3/+WVx33XWGSGOYDwMJkIDeBJ5//nl5T2NVyx07duhdGYfWR1aoP//8c3HhhRfKBj355JNF3Pq0HLY/o5GAlgSqVKki7+277rpLS/vTNTqSQj116lRx0kknyYbEcolffPFFulwyij906FDRr18/2006sXlnt27dRM2aNeWrTZs2tnExFAl96jVq1JAv5MtAAnEnMGfOHHl/o786DmvER06on3rqKaMBa9euLXbu3BnoNd23b1+jfKv1QiC8efPmlXHKli0rxRcXG45Nnz79KFt3794tEMe8KzN+BNjPfhQmfokpgebNm8v7qE6dOpEnECmh/s9//mOIZIkSJcS4ceMCbUCIMES3SJEi8t1KqHHutNNOE+ZB+xBiHIdYQ5xVgOgnijfOQbwZSCDuBNauXWvc75MmTYo0jkgINZ4E169f32i0Rx55RHqhlSpVElgqMYgAgcU0V4io8qoThRo/HBBynE8MEOTEc61btz5K0FUaeNSJeatzfCeBOBF4+OGH5X1TsmTJSFdbe6H++uuvpUBC5PB69dVXjQabNWuWuOmmmwJZaAniifLhKdsJNYQXccxdGYaxQkhPG2KvAro5rP4V0KNWhPgedwJ///23MdMYcyWiGrQWaiwmfvrpp0vxQ9fBRx99dEw7QTThYfsZ4N1CgCGsCHZCjQeCiGcXEs+rPmqz94wfBCuP3C5PHieBqBN46aWX5H11/PHHi82bN0eyuvaqEfLqqrGUEL7q1avbNtD+/ftFrVq1xOLFi32pEcQUfcsQWRXshBq2JvOGlcdt7r9G/jiOHyKUYdVnrcrlOwnElQBGUOH+iur+ploK9f333y8bBQ3TsmXLlNcmukD82ncNfeN4OAhBVSGZUJsFXcVX73bp1Hm+kwAJWBNQ/2qhCQsXLrSOpPFRrYT60KFD4tZbbzVEGg8SnIaOHTuKiRMnOo3uKJ56OJjo5doJLi4iCrUjtIxEAmkTaNu2rdQGeNdRC9oI9YYNG0TVqlUNkR4zZkxabfHVV19JkYTYexHwQBBdHuiWSAxuhVo9kDT3SSfmze8kQALWBLDOPPqp4RCNHTvWOpKmR7UQ6g8++ECcc845sgGwIMu8efNc4e7Zs6dIV+DtCoJnDKHGgub4q2V+YaYhLpZhw4bJ42qUB/qncdwuIE+cN3ej2MXlcRIggWMJDBw4UN5DWHPeK6fs2FKCP2KvGsHbYlmi6l6AgGFcNAa5uw1YfxoPHr0IsMfpCx42ghrrbSfEajKMF/YxDxKIKwFMdsO9mU7XaNhZhVqosa6FEsObb75Z/PXXXxnz7NKli5gyZUrG+UB87V7KM0a3COKorgz1o2M1NhpeN+oKMWcgARJwTwDPopRurFu3zn1GIUoZWqFWDwYA/N577/UMGbbiatq0qWf5WWUEcYbdSqBVHHjSGCGCSS2JXrXythPTqLR8JwEScE4A6/zgHsR6IFEIoRPqrVu3iquuusr4RXz22Wc953zDDTdYTs32qiA7oUb+yqsuWrSoXGEP/dhqDCi9aa9agPnEncCnn35qaMjcuXO1xxEqoQbcCy64QAL+97//LWbOnOkLYEyW8XO2YjKhRoUg1uiPVn/P4GVjxEeil+1L5ZkpCcSEQKdOneQ9hrWrdQ+hEerXXnvNGFpz6aWXCgyn8ytgqF8YxlpCmNWIEL/qynxJIK4EsPtL7ty5pVjDOdM5hEKon3jiCcO7RLdEEJ4ltp4PekMBnS8U2k4COhJ48sknpbYUKFBA6w2tsy7U2EpHdQEEua0OFlB65plndLz2aDMJkEAaBEqXLi01BjuY6xqyJtTwmuE9K5GGVx1kQH94ixYtgiySZZEACWSBAPZLVTqzcuXKLFiQeZFZEWr0P6MfGvAw5RP900GHgwcPilKlSokDBw4EXTTLIwESCJiAGv7auHHjgEv2prjAhRojOTCiAyKNER7wbLMVsKLesmXLslU8yyUBEgiIgNomD7qDZR90C4EKNcZEq78gGCuNMdPZDJj56PWKetmsD8smARKwJ9C9e3epP+XKlbOPFNIzgQk1ZhcqkcaswzAEiHT//v3DYAptIAES8JnAb7/9JvLlyyd16Omnn/a5NG+z912osT4H1ulQIg0vNizhk08+EWH50QgLE9pBAlEmMHz4cKlFmGS2a9cubarqq1BjpTuseKdE2moxomyS2rRpk7juuuuyaQLLJgESCJiA0iQs0KZL8E2osWY01o6GSGMtaawpHbbw559/ygWSwmYX7SEBEvCPADbFVs7j0qVL/SvIw5x9EWoszq9AYFcWTNkOa6hYsaLYu3dvWM2jXSRAAj4QwIgvaBTmcugQPBdqLNatRBr7G4Z9lwWMPvnpp590aCvaSAIk4BGB1atXGzrlxfr0Hpllm42nQl2vXj2j8hDp999/P/QvrKw1YcKE0NupA0vaGP7rnW30Txs1a9ZM6lXx4sVtBTIsJzwT6iNHjggsfKK8ab4736qLrMiK10D2roFLLrlEhL2v2jOhxi8P+n0KFy4sp2ZjejZfZMBrgNdAmK+BQoUKaTHpzVOhDsvfBNpBAiRAAlEiQKGOUmuyLiRAApEkQKGOZLOyUiRAAlEiQKGOUmuyLiRAApEkQKGOZLOyUiRAAlEiQKGOUmuyLiRAApEkQKGOZLOyUiRAAlEiQKGOUmuyLiRAApEkQKGOZLPqXam+ffvKGa54twrYGDlv3rwyzsaNG62i8BgJRIoAhTpSzRmNyixYsECKcOvWrS0rlErILRPxIAloTIBCrXHjRdV0eMlY+6JGjRrHVFF509ihA58ZSCAOBCjUcWhlDesIoUb3RmKgN51IhN/jQIBCHYdW1rCOZcuWlV612XTlaRcpUoTetBkMP0eeAIU68k2sZwXR7QGvGv3VKqDPGsfCtvemso/vJOAXAQq1X2SZb0YEVBeHEmqzN51RxkxMAhoSoFBr2GhxMHno0KHSe1ZD9JQ3rYQ7DgxYRxJQBCjUigTfQ0VADdGDUCtv2moUSKiMpjEk4BMBCrVPYJltZgQw9A790RBqetOZsWRq/QlQqPVvw8jWAELdtWtXKdj169ePbD1ZMRJIRYBCnYoQz2eNgBr5AcFG9wcDCcSVAIU6ri2vQb3hRUOk7aaSa1AFmkgCnhCgUHuCkZl4TYBTxb0myvx0JkCh1rn1Imy7GkethudFuKqsGgmkJEChTomIEYImsHz5ctnlwaniQZNneWElQKEOa8vEzC5MC1+4cKHo16+fsdY0J7fE7CJgdW0JUKht0fBEkATw0FC94ElPnz49yOJZFgmEmgCFOtTNEx/j0N0BD5pedHzanDV1ToBC7ZwVY5IACZBAVghQqLOCnYWSAAmQgHMCFGrnrBiTBEiABLJCgEKdFewslARIgAScE6BQO2fFmCRAAiSQFQIU6qxgZ6EkQAIk4JwAhdo5K8YkARIggawQoFBnBTsLJQESIAHnBCjUzlkxJgmQAAlkhQCFOivYWSgJkAAJOCfw/yym/vjLAJiZAAAAAElFTkSuQmCC[/img][br]Explain how you know the triangles are similar.[br]
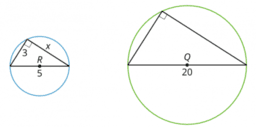
How long are the sides labeled [math]x[/math] and [math]y[/math]?[br]
Under what conditions is there an Angle-Angle Quadrilateral Similarity Theorem? What about an Angle-Angle-Angle Quadrilateral Similarity Theorem? Explain or show your reasoning.
IM Geo.3.9 Practice: Conditions for Triangle Similarity
What is the length of segment DF?
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAfMAAAElCAYAAADwaAt5AAAgAElEQVR4Ae2dBbgV1dfGlRBBJCQEkZDuLgUJaURBRAwQUEEJSREEKQFBQpCSEpCQkhIllBAQQboxkE5BBAFJdX3Pu//fXOfOPTGnJ979PPe558zsmdnrt+fMO7vWukuYSIAESIAESIAEbE3gLluXnoUnARIgARIgARIQijlvAhIIksCuXbtk3bp1Cf6CPB0PIwESIIGgCVDMg0bHA91OoFixYnLXXXfF+8uePbvbsdB+EiCBGBCgmMcAOi/pDAIQ8m+//dYZxtAKEiABWxOgmNu6+lj4WBGAiEPML126FKsi8LokQAIkEEeAYh6Hgh9IwDyBvn37CrvUzfNiThIggcgSoJhHli/P7lAC9evXlxw5cki/fv3i/qZNm+ZQa2kWCZCA1QlQzK1eQyyfJQmgVY4JcJUrV477o5hbsqpYKBJwBQGKuSuqmUaGkwDGyTn5LZxEeS4SIIFQCVDMQyXI411HYPHixUrMXWc4DSYBErAsAVeJ+ciRI+PGNzHWuWTJEstWDAtmXQKY/IYudiYSIAESsAoB14i51jWqH+dMnTq1FC9e3Cp1wXLYhADGyTt27GiT0rKYJEACbiDgGjH3tC4Y7jg59umG2zy8NuIlEPeN/g8Cz0QCJEACsSLgGjH31DWqtdYxBspEAiRAAiRAAnYl4Boxx7rg5s2bx6sndJWilUUvXvGw8AsJkAAJkIDNCLhGzCHacPJRpUoV9YfPEHh0tTORgJHAzp075cKFC8bN/E4CJEACliTgCjE/evSoGt9ESxzd7VqXO4SdrXJL3pcxK9SqVauUm1ZtPLxnz54xKwsvTAIkQAJmCbhCzD2tC4aIw4sXlqsxkYBGoGDBgvEmtkHUEbOciQRIgASsTMAVYo6WuKfZxthmHEe3cmWxbJElcPLkyQRCDjH/4IMPInthnp0ESIAEQiTgCjH3tC5Y63pnyzzEO8hhhz/00EMJBH3y5MkOs5LmkAAJOI2AK8QcratOnTqp7lJ4fcPnNGnSeGytO62CaU9gBBAsRRsvx/+UKVNKkSJFZNu2bYGdiLlJgARIIIoEHC/maIGjZa7/Q9c6I1xF8S6z0aUOHz6sxLxDhw7y/fffy5kzZ6RMmTKSJUsW+eabb2xkCYtKAiTgJgKOF3M3VSZtDZ1Aly5dBF3tt2/fjjsZPtepU0dSpEghc+fOjdvODyRAAiRgFQIUc6vUBMthCQL33HOPvPnmmx7L0rRpU9VqHz9+vMf93EgCJEACsSLgCDHfu3evzJ49W3766adYceR1HUBgw4YNSqzXrFnj1Rr4KsBY+qBBg7zm4Q4SIAESiDYB24v5O++8ox6u2qSlgQMHRpshr+cQAs8//7yp0KYDBgxQ91zXrl0dYjnNIAESsDsBW4v5jz/+GE/INUE/d+6c3euF5Y8BAdw/iHNvJn388cfq3nvttdfMZGceEiABEogoAVuL+aJFizyKOT12RfSeceTJ58yZo+4lDNmYTfPmzVPHNGzYUC5fvmz2MOYjARIggbATsLWYnzhxIoGYJ0uWTK5evRp2UDyhswlUrFhRqlWrFrCRGF/HWnT4+ccySCYSIAESiAUBW4s5gA0ePFjuvvvuOFHH0iImEgiEwI0bN9T9M27cuEAOi8u7e/du5ee/WLFismPHjrjt/EACJEAC0SJgezFfunSpehD36dNHhTgtV65ctNjxOg4hMHz4cMGStLNnzwZt0alTp6RUqVKSLVs2Wb16ddDn4YEkQAIkEAwB24t5t27dlJj/9ttvMnr0aPX5yy+/DIYFj3EpgUceeUReeOGFkK1HC79mzZqq2/3zzz8P+Xw8AQmQAAmYJWB7MX/sscekdu3acfbmy5dPSpYsGfedH0jAFwHNfev8+fN9ZQto34svvqheKidOnBjQccxMAiRAAsESsLWYa04+9JHP4J0LS4ww052JBPwR6Ny5s/K7fufOHX9ZA9rfvn17dR8yfGpA2JiZBEggSAK2FnN44YJwY725PhUuXFhFutJv42cS8EQAY+UQ3kgkrFnH/dm9e/dInJ7nJAESIIE4ArYW87p160rZsmXjjNE+fPLJJ+ohyqAYGhH+90RA69lZu3atp91h2TZ27Fh1L7Zq1Sos5+NJSIAESMATAduKOZx7pE6dWnr37u3JLilRooRg/JyJBLwRaNy4sRQvXtzb7rBt1xzSNGrUiD4QwkaVJyIBEtATsK2Ya+40EXPaU5oxY4ZqEc2cOdPTbm4jAXV/vPfee1EhgVjoyZMnV45pjh8/HpVr8iIkQALuIWBbMW/SpInkzp3bZ02hCz5nzpw+83CnOwloreV9+/ZFDcDOnTsla9asqtcIjmaYSIAESCBcBGwp5nDjmj17dmnXrp1PDtoDe+rUqT7zcaf7CFSoUEGqV68edcPRKkfXfo4cOeTbb7+N+vV5QRIgAWcSsKWYayJtxjkMHtpoDTGRgEbg2rVrqosdQzWxSH/99Zd6kcCcj4ULF8aiCLwmCZCAwwjYUszRIn/ggQfEzNrgBQsWqAc3HXg47M4NwRy4b0VAnliHykX8dCxdw+oLJhIgARIIhYDtxBytKgS0gJctswkRrTJlymQ2O/M5nAC6uAO5fyKJo23btkrQhw0bFsnL8NwkQAIOJ2A7MV+xYoV6+E2fPt1U1aBL8/3331fHjBkzxtQxzORcAr/++qu6F6zkOx1BgtBC79Gjh3PB0zISIIGIErCdmL/77rsq5OmSJUsEfrWvXLkSDxC+Y/u6detk8uTJgpCos2bNkscff1x1zcfLzC+uIwD3rQ8//LD8/ffflrJ91KhRStBbt25tqXKxMCRAAvYgYDsxr1y5siC4ClpWH330kfTq1Us6deokXbt2Vf/xHduxH0uBbt26pWpi+fLl6mE5YsQIe9QMSxkRAkmTJpUOHTpE5NyhnhQvnWihYyz9+vXroZ6Ox5MACbiIgK3EfPPmzZIkSRLRB1bR6gqT4f7991/tq8f/Tz75pNx///0e93Gj8wmsX79eiaWVl4StXLlSTc6rUaOGIEY6EwmQAAmYIWArMcckIbRcjIFVzBiKPKtWrVLHDxkyxOwhzOcgAnDfCje/Vk/btm2Thx56SEqXLi1wW8xEAiRAAv4I2ErMGzRo4DGwij8j9ftxjnvvvVe/iZ9dQgAvgv3797eFtUeOHJGiRYtKrly5BD0KTCRAAiTgi4BtxPynn36S9OnTew2s4stI/T6tq3XgwIH6zfzscAKzZ89WvTL79++3jaWYzFm1alVJmzatYMInEwmQAAl4I2AbMcfMdLSsvAVW8Wagp+3PPfecJEqUyNMubnMoAXgCxDi0HROireHep1tiO9Yey0wC0SFgGzFv0aKF38AqZpFt2rRJPRyxvpfJ+QQuX76s6nv8+PG2NRZL1iDoH374oW1tYMFJgAQiR8AWYn7+/Hkl5P4CqwSC6aWXXlIPx9u3bwdyGPPakAAmTmKexG+//WbD0v9XZPhYgKBj+SUTCZAACegJ2ELMNf/qZgKr6I3z9RkzhvFgpNctX5ScsQ/uW/Hy5oQEPwm4b+EGlokESIAENAK2EHM4hUmXLp2pwCqaYWb+N2/eXD0Y4fKVyZkEDh06pOoYL4ROSTNmzFA2wb+85hTJKbbRDhIggeAIWF7M//nnH7XeNhKBMfbs2aMeivAex+RMAngRRAhc3EdOSsuWLVMOlGrXri1nz551kmm0hQRIIAgClhfz1atXK8E1Blbp2LGj2u7Lm1ffvn0T5Dl69KhgO/4WL14srVq1UnkuXboUBD4eYnUCcN+Ke8WJacuWLSoaYNmyZeXAgQNONJE2kQAJmCRgeTHv16+fCqyin7wEAc+ePXsCodbbvGvXLo959A92uIXVvMLpt+vPw8/2JaD5FEDQHacmRIErVKiQ5MmTR7777junmkm7SIAE/BCwvJhXr15d0JWoJbSgMaEJgo6JQJ5a5loetLyNedAi1yd812JKY9Y8k3MIwJ9AyZIlnWOQF0uw9K5SpUrKqdLSpUu95OJmEiABJxOwtJgj6lny5MnjBVapX79+XLepUai1ikIrG/mQjHkw6U1LaJmjBa/FuG7Tpo22i/8dQAB17yZPfw0bNlTOkIxDUg6oSppAAiTgh4ClxRyhTPFA1gKrTJs2TXWda+PbRqGGrWiNowveWx6IN8ReGzPX+GAbznf69GltE//bmIDmvtVtY8naHBBPkQVtXJ0sOgmQgB8ClhZzdJNicg8SJq6lSZNGtaQ1m4xiDgFHHn3XuzGPdqzx//HjxyVx4sTSsmVL4y5+tyEBxLyvVauWDUseepHhOwH3PT0chs6SZyABuxCwrJgfO3ZMMmfOHBdYpXLlyqo1rQdrFGp9F7yWz5hH2+7pP5aoIT+uzWRfAhcvXlT1OGHCBPsaEWLJhw8frhi0b98+xDPxcBIgATsQsKyYY9wPworAKugyRIsbM9v1f9gPn+3ofscfvuv347OWB5/9JazXxRi9flzd3zHcbz0CcN+KenT7hEbtN9GkSZOwO1yyXq2zRCTgbgKWFXOM/WG5DRIeSmiZG/8g1MWKFVNj4P7y4FgzSeui/OWXX8xkZx4LEsCcCQgYkwhcICNCYN26dV3/csP7gQScTMCSYn716lUpUKCA+AusAjHXj497qigzefTH/f7775IqVSrH+PLW2+aGz4h7jzpfuHChG8w1ZSOiBGbIkEEeffRRAR8mEiAB5xGwpJhjrSweyP4Cq5gRajN5jNWKiUM4zm0zoY0c7Pgd7luzZctmx6JHtMzoacqfP7/ky5dPIO5MJEACziJgSTF/++23TQVWQatcW4LmrVrM5DEee+XKFXX9Ro0aGXfxu8UJJEmSRCDoTAkJ/PHHH1KxYkXJmDGjwLc7EwmQgHMIWFLM0R0Y65CVcDaC1vnu3budU9sOtwRuW1FnGzZscLiloZmHVR/wWT9z5szQTsSjSYAELEPAcmK+ceNG9UCOtRermzdvqiAWmic5y9QYC+KVAPwSlCpVyut+7viPwGuvvaZ+Z6NHj/5vIz+RAAnYloDlxPz9999Xs2/1gVViRXfIkCHqgbdt27ZYFYHXDYAAWuW4f5jMEejWrZu6v9977z1zBzAXCZCAZQlYTsyxhEYfWCWW5BADG7GwUSYmaxP47LPPlDAdPHjQ2gW1WOm0F1ZGDbRYxbA4JBAgAUuJOR7EWBZmJb/SI0aMUCIB5zVM1iUA961WeQm0LiXPJZsyZYq6x5s1ayb//vuv50zcSgIkYGkClhLzcePGqYeKFljFKuRy5swpCMXKZE0C8PSGLvaJEydas4A2KNWSJUsUw6eeekrga4GJBEjAXgQsJeaYwV6uXDnLERwzZox60GG2NJP1CAwdOlRSpEghFy5csF7hbFSi7777Ti3JrFChghw6dMhGJWdRSYAELCPmmPAGZx+9e/e2ZK3A4YZZl7CWNMDBhYL71qZNmzrYwuiZhl6xvHnzSsGCBWXLli3RuzCvRAIkEBIBy4j53LlzVevXqmPT6MJFV+6qVatCAs6Dw0sAXvpQL4sWLQrviV18NnSzw9cDohauWLHCxSRoOgnYh4BlxLxt27ZxgVWsiq9IkSKCiVZM1iGAWdhomTOFnwDGz5MlSyazZ88O/8l5RhIggbASsISY37lzR4oWLeo3sEpYLQ/iZFOnTlWtwOXLlwdxNA+JBAG4b+3cuXMkTs1ziqgQw+j5GDt2LHmQAAlYmEDYxRy+0LWY4h999JFf3+lg88033yiR9BdYxQocS5YsKaVLl7ZCUVxfBtxrEBpM3GKKHIG33npLcR4wYEDkLsIzkwAJhEQgrGLet29fSZ06tYovjs+YMJYmTRq/gt6zZ09Jnz69oIVu9TRr1iz1YMNSHqbYEkAgHL5YRacOBg8erO77Ll26ROeCvAoJkEBABMIq5mglLV68OF4BihUrJhB2X6lSpUoxD6ziq3zGfVg+B7uYYkcA3vlwvw0aNCh2hXDZlSdNmqSYt2jRwmWW01wSsD6BsIs5uj71Ca1zX2K+fft2SZw4scQ6sIq+zP4+z5s3Tz3UPv/8c39ZuT9CBLQeEqs5GIqQuZY57cKFC9W9jwBE/sIPW6bQLAgJuIBAWMW8efPmUrx48bgf+bRp01S3+9GjR72iHDZsmGUCq3gtpIcdiAtdoEABD3u4KRoEsHSqTp060bgUr2EgsH79ejV8hh61w4cPG/byKwmQQCwIhFXM8aaON3aMk0PU0RW9a9cun3Yhvx0fyhhOQDcvl+34rN6I7Dx79qxij25fptgQwPr+XLlySeHChYVRBWNTB7wqCegJhFXMIdw5cuRQE9/QSofYYWa7t3TkyBHlPtJKgVW8ldXT9qpVq0ru3Lk97eK2CBJApK/77ruPPsQjyNjMqeG1EfNHsmTJolakmDmGeUiABCJDIGxijlY5WuR6YYa4w6GHtzFzLVqTXcc9v/rqK/XCYqfx/sjcRtE9K9z+vvzyy9G9KK/mkQAmIiJEMHzjw4sjEwmQQGwIhE3MMT7uyRMXtkPkPSW03q0YWMVTWb1tq1Wrlke7veXn9tAI7N27V71AGVdNhHZWHh0qAbxcoSdu/PjxoZ6Kx5MACQRBIGxijoerJ9FGS93TMq4///xTjblZNbCKWZaaw5vJkyebPYT5QiDQoUMHNZQTwil4aIQIwBMflwtGCC5PSwJ+CIRNzNHNDocxDRo0UJPe8P3TTz9N0PWulUeLn2zVwCpaOc38r1evngpKYSYv84RGAMsY6bgkNIaRPHrgwIFK0Lt27RrJy/DcJEACBgJhE3OcF0vQ0HWO7na8oWONObrZPSUEyECoRSckza3oxx9/7ARzLGvDmjVr1H21ceNGy5aRBROZMGGCqqfXXnuNOEiABKJEIKxiHkiZS5UqJW+++WYgh1g67zPPPKNc0lq6kDYv3LPPPitlypSxuRXuKD4cKuGFvmHDhnLlyhV3GE0rSSCGBGIi5hs2bFA/dDsEVjFbNxguwMNr1KhRZg9hvgAI3Lp1S/GFj3AmexBAj9X9998vVapUkWPHjtmj0CwlCdiUQEzE/L333rNNYJVA6rVx48Zq3kAgxzCvOQKa+9aff/7Z3AHMZQkC+/btk0ceeURNgt25c6clysRCkIATCcREzKtXry5NmjRxHE94wkLrfPjw4Y6zLdYGlS9fXq1njnU5eP3ACcBjH6LbwT/A6tWrAz8BjyABEvBLIOpivn//frn33nttFVjFL0VdBrykJE+eXLeFH0MlcOrUKfWS9Mknn4R6Kh4fIwIIb1y7dm1JmTKlMEBRjCqBl3U0gaiL+ZgxY1SUNLiCdGLavXu3Eh6G5gxf7cJ9K0Tg4sWL4TspzxQTAnjZRe/VxIkTY3J9XpQEnEog6mLeqFEjWwZWCeQGeOWVVyRJkiSBHMK8PghkzZpVLXn0kYW7bEQAjn8g6B988IGNSs2ikoC1CURVzDF2lilTpnj+262NJ7jSHTx4UD2sMNGPKTQC8O+PBz+cDDE5h0D//v1VvXbv3t05RtESEoghgaiKOcKF4sFs18AqgdTT66+/rmxFIAqm4AmgFYfZ0EzOIzBu3Dj1G2nVqpXzjKNFJBBlAlEVc/xoMSvZDenQoUPqQfXuu++6wdyI2ZgoUSJ56623InZ+nji2BBBpDS/4GH7766+/YlsYXp0EbEwgamIOpx/58+eXPn362BhXYEWHhzs8qG7evBnYgcytCGhBbJzgv59V6p0AlqshPn21atXk5MmT3jNyDwmQgFcCURPzlStXKmFz04P5+PHjyuZu3bp5rQDu8E4A7lvLli3rPQP3OIbAnj171Dr0EiVKCD4zkQAJBEYgamKOiS5OCawSCGItLCT9UwdCTeT69evqRYgzngPjZufcp0+flpIlS6oQt3AFy0QCJGCeQNTE/NFHH5X27dubL5lDcp45c0YtU4OoM5knMHPmTCXmv/zyi/mDmNP2BDAcV6NGDeUWeeHChba3hwaQQLQIREXMt27dqh7MTgqsEkgFoVcCY+d0emKeGiZKPvnkk+YPYE5HEXjhhRfUb4Ze/xxVrTQmggSiIubw4JUhQwaBS0c3pt9//11SpEgh7dq1c6P5AduszTWYMmVKwMfyAOcQ0CaQDh061DlG0RISiBCBqIh5nTp1HBlYJZA66dWrl2ppnDt3LpDDXJkX4+QInfnHH3+40n4a/R+Bvn37qt9Njx49/tvITyRAAgkIRFzMDx8+rB7M06dPT3BxN234888/1TggnMkw+SYA960tWrTwnYl7XUNg9OjRStBbt27tGptpKAkESiDiYo4xr8SJE4tTA6sEAlxzYcm1tN6pbd++XT24v/jiC++ZuMd1BDTvkY0bN6bfBtfVPg02QyDiYo4oSXXr1jVTFsfnuXHjhqRPn14QiIXJMwGseMiZM6fnndzqagJwIoTwyZjtjlUiTCRAAv8RiKiYX7p0SdBl+tFHH/13RZd/Gjx4sGp5YviBKSEBuG/t2rVrwh3cQgIisnPnTnn44YeldOnSsn//fjIhARL4fwIRFfNFixYp4XJDYBWzdxQCr2TOnNn1EwI98VqxYoW6XzZt2uRpN7eRgCJw4sQJKVasmOrB2bBhA6mQAAmISETFHF2mbgmsEsjd9OGHHyrR+umnnwI5zPF5GzZsKOXKlXO8nTQwdAIYsnriiSckbdq0DI8bOk6ewQEEIirmRYoUcVVglUDuh2zZsgkm8zD9j8DVq1fVCw58EjCRgFkC+A3BIdPUqVPNHsJ8JOBIAhET83Xr1qkfmZsCqwRyh4wZM0bx2bdvXyCHOTYvli7ioYzQsUwkEAiBNm3aqHsHPV5MJOBWAhETczh7yJcvn1u5mrI7V65c8swzz5jK6/RM6F6vV6+e082kfREi0Lt3byXocM7ERAJuJBAxMa9UqZKpwCqY8f7pp59Kv3791N/Ro0fj1YN+P/LhuzHhGE/bjfms9n3ChAnqAYQZuuFMu3btEvSM4L8d0pEjRxQHdpXaobasW0asmkHvTtu2ba1bSJaMBCJEICJijq5jLDHyF1hl2rRpkiZNGjUztXnz5tKxY8d4AoQwiNhfv359QUsfM1jxXS/42I7z4P/IkSMjhClypy1QoEDYAoqAAfjggab9gZnVE9y3pkqVypYvZFZn67byzZo1S937L774omtjQbitzmnv/whERMzhftFfYBUINQQHQuwtQYgg8PpUuXJlgfAj4RyLFy+O2w0xs1sLHa1RcPjhhx/i7AjmA154UqdOHY8nWNihdY51w3SkE0yt8xhPBFauXCn33HOP1K5dm54nPQHiNkcSiIiYYxy4adOmPoFBfDRR9pbRKE7IB3GHoCNByPVihRcDfavd23mttr1o0aJSs2bNoIuFlxiw0rMI+mRRPnDLli3qZWbp0qVRvjIv52QCcAsMfw5ly5YV+rlwck3TNo1A2MX89OnT8sADD8iMGTO0a3j8j9YoWta+EoS7ePHica1tiBW6kbXWOFqeeCHAdmyDqNkxzZw5Uwnad999F3DxwQBM7DjEAGPhiwATAZlIINwEjh07JoULF5Y8efIIV9WEmy7PZzUCYRdzjFklSZLEZ/eW1sUOEc6RI4cSMog7ImXpu8nxGS14iBX2Zc+ePV43MmAiD4Tc34uB1cAbywP3lFWrVjVu9vsdvRFgp+fm9yALZbj77rulW7duFioRi+IkAteuXZMqVaqomAj+5vA4yW7a4j4CYRfz1157zW9gFU3M0V2udYvjP8bI9V3vEChNxJEXoo5Z705M8+bNU6K8Zs2agMwDL23YIaADLZD5q6++UjZv3rzZAqVhEZxM4Nlnn1WTct0eitnJdex228Iq5nCxiIhX/gKraGKuCblWCWhho5WpJaO4oyWP1rlxUpyW3+7/H330UalQoUJAZkDI7SrmcN9Kd78BVTczh0DgjTfeUM8Xuw5JhWA6D3UBgf+UMwzGLl++XP1Y4InJlycviLinrmFN5FEU7bOx+9go+GEotmVOoQWmwWxcs8muYn758mV1DwwdOtSsqcxHAiET6Nmzp7rv+vTpE/K5eAISsBKBsIr522+/LWXKlFFCjLXD48aNE2/BRDyNf2P8F7OykTQxN8Lytt2Yz67fIc6YgWs2YdIf5h0YX3rMHh+rfNqSvF9//TVWReB1XUpAC3SEyZdMJOAUAmEVc0zi0s8o37p1qwwYMEDmz58vf//9dzxmEG6MgUOckfAf3/XHQ/D1k+LQosfsdkyKc2rSxpHNTtbRejn0nMAGQxJWTnDf+tRTT1m5iCybgwlosQCaNGki//77r4MtpWluIRA2MdfWCxuXgEDEP//8cxk2bJicOXMmHlcIN1ri6HLHf72QIyMECS1V7Nf+MOHLbq3QeEab+FK9enUpUaKEiZz/y4KhB42jfnWA6RNEOSOGYFCfeKFjIoFYEcCwYOLEidWE3d9//z1WxeB1SSAsBMIm5uhW9xVYBWuoEQTBOOktLFY47CRff/21EruFCxcGZBleftDDofV2BHRwFDMPHjxYvXz8+eefUbwqL0UCCQmg9/DBBx8UTD795ZdfEmbgFhKwCYGwiXmtWrWkQ4cOPs3etm2bILrR2bNnfebjTlGthUKFCjkSBdy3vvrqq460jUbZjwAC/RQsWFA1RkJ1q2w/61lipxAIi5ij2zRZsmSC8V5/acOGDYIJKByn8k0KrWt0Rc+dO9d3Rpvt3bRpk7LLzL1iM9NYXBsTuHLlijz++OOSMWNGQfc7EwnYjUBYxHzSpEnqR3Dnzh1T9mNCHMbRmXwTqFatmoomVrJkSenUqZPggWP39Oabb0ru3LntbgbL71ACiCuRNGlSgSdLJhKwE4GwiDnCDfoLrKKHgklxmOXOAAh6KvE///PPP5IlSxbVitUm/9WoUSN+Jht+g/vW7t2727DkLLJbCLRs2VL97hD9kYkE7EIgZDG/ePGiZMqUyW9gFSMQjJ+PGTPGuNm13y9cuCB79+4VTH779A3UGwsAACAASURBVNNP5eWXX44n5Jqge1u3bwdwS5YsUTZxXNIOteXuMuKFE785p7qPdnftOtP6kMV8wYIFfgOreEM3fPhwx7bOr1+/LocPH5aNGzeqIQW85ffo0UOtm8dkQYQ9xfhcokSJPIq2t+2+POt542yV7ejCxKxhJhKwAwEsp4WgO9V9tB3qgGU0TyBkMW/Xrp08+eST5q+oy4nlagj/aZd07tw5tfYdE2SmTJkiAwcOFNgPH+OPPfaY5M2bV4V/1VrRxv9YC47xYgja008/LQhK884776gJgeAAN647duyQEydOyM2bNwWz2fXnsLOTFfTgwBY8IJlIwC4EtKiEzZo1s0uRWU6XEvAo5nDKgrCBZpx6YEnHqFGjgsJ39epVgQvYWM1sx/WxtnT9+vVq1jgCMCAcJxzT1K1bV7lVReCY+++/P56oagKLiTIPPfSQivYGRy8vvfSSeouHyE+cOFHgax0vLLhGMGuqT548qeJ9w3EOlvRhHN2uafLkyYoheiuYSMBOBOCNEXM96tWr53iHVXaqF5Y1PgGPYg4xg2D5615au3atyhfKRDa8CITLWQNeCk6fPi3bt28X/AAhqJhoBzsgtDVr1hTMDM+aNaskT57co0CnTZtWtbARvaxBgwbSqlUrQXAGRIL77LPPZPXq1bJ//37BGDeTeQLwN4/eCCYSsCMBhOlNnz69imrIF1I71qDzy5xAzDVf32biZKO1GOoYKFyR4qXAW0J0rYMHDwrifM+ZM0dNmoPb17Zt20rjxo2latWqUqRIEcmcObMau9dazdp/rH+HkxK4R4WYY9Z9586dZdCgQYJgH+gyR9c2XgLs3PL1xs8K2zFpD/WBiX1MJGBXApivAi+X6I3EBF4mErASgQRiji5dCDkEE0FNPCW0eNHChVAGGn/79u3bcvz4cfVjWLFihSAUIcaj0Pp9/fXXBZOk4LyhQIEC6k1YE2X9/3Tp0kn+/PlVPoxXt27dWs06nTBhgmDGNN6i8VKC+OpMgRHAUIM3d7Bgitm96LHAf2/5jFfEixOC6DhhnbzRNn53FwE0LvDMwwoerDxhIgGrEIgn5prXMTy0tc/GgqL7Wi+s+Aw3rnhrhYhiP1q8iFON8edXXnlFRcdCCx6Tv/BQNx6PLu9s2bJJqVKl1Fg1XH1C3DEDfN68eWpM++effw5q3NlYfn73TADzJCDSqBtjwBscAb/vqDu86EHwMXThKTiOp7NjvTwm+zGRgFMIYMgIjRn0FjKRgBUIxBNztMq1cXJNzI0RytB6NooxJocYt2XIkEF1f2NiGLq2u3btKliKhlnbq1atkn379nHc2Qp3wP8LNaKtaT0ynsQc9wXuD33Swtjqtxk/YwIg7o1ly5YZd/E7CdiaABoquLfHjRtnaztYeGcQiBNzbQkGuqnXrVun/nCjGrtSMfvcKNyY8Y1x51OnTiWIW+4MTM62Ai9s2soFCLY3MTfGkddCr/qig6V7efLk8ZWF+0jAtgS05yEm2jKRQCwJxIl59uzZE4g0RBsPbH1Ci/ree++Nlxdj1UzOIOBNzLWeGk30MRSDORWehF9PAvcQ1tIzkYBTCQwZMkQ9D7t06eJUE2mXDQgoMccYKMY/jV3qxYoV8/iwhqDjjRRd7kuXLrWBmaJsa9GiRbwxe2Ovgy0MiXAhvYk5Lqu1xCHiEGncN74S4rEj35YtW3xl4z4SsD0BOJHCvY5nDBMJxILAXRBwTGzy1MLCg10bQ49F4cJ1TdgIAcLLCQQc37W/cF3DKefxJubghQcVenBwr+A/mGJinLeECXXwjMdEAm4g8MUXXyhBx3BUME6i3MCINkaOwF3ag9nTJTxNevKUz+rbzKyZt7oN0SqfNzEHQ7wMQdS1hG14EdRv0/adP39ePdgw6ZGJBNxC4Pvvvxc4nqpUqZIcO3bMLWbTTgsQuMvXumK0YrUxUguUNegiYAjBOPYf9MkcfqA3MUcXoqdhCWz3xBbzKLDvyJEjDidG80ggPgEso8Wkz8KFC8vOnTvj7+Q3EogQgbgJcBE6f8xPi25giApaj3gxgbMT/PnqHo55oWNYAG9i7umFCEy9iXyZMmXEOPs9hmbx0iQQVQIILFS+fHmBjwW4gGYigUgTcLyYozUJwcH4LoYNMKyA7mFvIhRp4FY/vzcxBzt0qcMlK16EsHwRY+LGrnfYd+DAAcV3+vTpVjeX5SOBiBJAcJYUKVLI/PnzI3odnpwEXCPmxq5gp8wHCPctDC7ehlawHWKPVjr+46XI03g51txi3BBR6ZhIwO0EtMYDl/C6/U6IrP2uEXMjRq3FbtzO76ETQFjYli1bhn4inoEEHEIAa9DRG4g4BUwkEAkCjhdzODfBjwj/9UlbM63fxs+hE0D3O3gjGh0TCZDAfwQg5PhtwLU1EwmEm4DjxRzA0CVsdOagdROHG6jbzwf3rXnz5nU7BtpPAh4JTJ48WQk6Aw95xMONIRBwhZhjwhbGeatUqaJmsmMyHJyeGFvrIXDkoSLKLz9aHj169CAPEiABLwTQK4jfCcI9X7t2zUsubiaBwAi4QsyBBBO1sKYes9kxkcvTxK3A0DG3kQBm7OIhtXXrVuMuficBEtARQDRBrYFx4sQJ3R5+JIHgCLhGzIPDw6MCIYClahUqVAjkEOYlAdcS+PHHHwURJ7G8c8+ePa7lQMPDQ4BiHh6Orj/L2bNnVat8xIgRrmdBACRglsCFCxekbNmykjVrVo8eFs2eh/lIgGLOeyAsBMaNG6fEnPMQwoKTJ3EZgTp16kjKlCkFkQaZSCAYAhTzYKjxmAQE4L4V3exMJEACwRFo2rSpeiHGjHcmEgiUAMU8UGLMn4DA3r171UNoxowZCfZxAwmQgHkCnTp1Ur+lIUOGmD+IOUlARCjmvA1CJoDANQ888ACX2YRMkicgAZGBAwcqQe/evTtxkIBpAhRz06iY0RsBuG9t1aqVt93cTgIkECABLYQwf1cBgnNxdoq5iys/HKavWbNGtSJWrFgRjtPxHCRAAv9PYMGCBeq31ahRI7lx4wa5kIBPAhRzn3i40x+Btm3bSr58+fxl434SIIEgCCDWAWa5P/HEE3L69OkgzsBD3EKAYu6Wmo6Anbdu3VIth549e0bg7DwlCZAACBw4cEBy5MghJUqUkH379hEKCXgkQDH3iIUbzRCYM2eOEvPt27ebyc48JEACQRL47bffpFSpUkrUN2zYEORZeJiTCVDMnVy7Ebatfv36UrFixQhfhacnARIAgX/++Udq1qwpqVKlkiVLlhAKCcQjQDGPh4NfzBI4deqUapUjeA0TCZBA9Ai89NJL6rc3derU6F2UV7I8AYq55avImgUcPXq0eqAcO3bMmgVkqUjAwQQ6dOigfn/Dhw93sJU0LRACFPNAaDFvHIHSpUureMxxG/iBBEggqgT69++vBJ0TUKOK3bIXo5hbtmqsW7Bdu3aph8jMmTOtW0iWjARcQODjjz9Wv8XWrVu7wFqa6IsAxdwXHe7zSKB3796SLl06+euvvzzu50YSIIHoEZg/f74S9MaNG8vt27ejd2FeyVIEKOaWqg57FCZz5szy+uuv26OwLCUJuIDA2rVrJUWKFFKjRg05d+6cCyymiUYCFHMjEX73SeDrr79WrYCVK1f6zMedJEAC0SWA6IVZs2YVzGc5ePBgdC/Oq8WcAMU85lVgrwJgbC5//vz2KjRLSwIuIXDmzBnlKS5nzpyyceNGl1hNM0GAYs77wDSB69evq1Y5Z8+aRsaMJBB1Anfu3JHq1atL2rRpZenSpVG/Pi8YGwIU89hwt+VVZ82apcR8x44dtiw/C00CbiLw/PPPq9/r9OnT3WS2a22lmLu26gM3HO5bH3/88cAP5BEkQAIxIdCuXTsl6PTUGBP8Ub0oxTyquO17sePHj/OhYN/qY8ldTKBfv37qt4slpUzOJUAxd27dhtUyvNnffffdAlFnIgESsBeBsWPHKkFHS53JmQQo5s6s17BbRfetYUfKE5JAVAnMnTtXCfqLL76oIrBF9eK8WMQJUMwjjtj+F0C88rvuukswAY6JBEjAvgRWr14tyZIlk1q1asmFCxfsawhLnoAAxTwBEm4wEsBStPTp0wuWpjGRAAnYm8Du3bslS5YsUrZsWfn555/tbQxLH0eAYh6Hgh+8EaD7Vm9kuJ0E7Eng1KlTUrRoUcmTJ49s3rzZnkaw1PEIUMzj4eAXI4Hly5erLna4cWUiARJwDoGbN29K1apVVdCkZcuWOccwl1pCMXdpxZs1u2XLlnTfahYW85GADQk899xzkihRImFIYxtWnq7IFHMdDH6MT+Dq1auqVf7uu+/G38FvJEACjiLQpk0b9VsfPXq0o+xykzEUczfVdoC2wg0kZrHv3LkzwCOZnQRIwG4E4FQGv3c4mWGyHwGKuf3qLGolfvrpp+m+NWq0eSESiD2BUaNGKUHv0KFD7AvDEgREgGIeEC73ZD5y5Ij6UX/00UfuMZqWkgAJyGeffaZ++02bNiUNGxGgmNuosqJZ1OHDh6tJMSdPnozmZXktEiABCxD45ptvJGnSpFK3bl35448/LFAiFsEfAYq5P0Iu3V+qVClp2LChS62n2SRAApgrkylTJilfvrz8+uuvBGJxAhRzi1dQLIq3ZcsW1c2G7jYmEiAB9xI4ceKEFCpUSPLlyydbt251LwgbWE4xt0ElRbuI3bt3V+5bb9y4Ee1L83okQAIWIwA3zpUrV5aMGTPKypUrLVY6FkcjQDHXSPB/HAF0rb3xxhtx3/mBBEiABJ599llJkiSJzJ49mzAsSIBibsFKiWWRvvzyS9XFjgkwTCRAAiSgJ4CXfKxFR3x0JmsRoJhbqz5iXppXXnlFChQoEPNysAAkQALWJACPkBD0/v37W7OALi0VxdylFe/J7MuXL6sfaa9evTzt5jYSIAESUARGjhypnhWdO3cmEYsQoJhbpCKsUIypU6eqH+iuXbusUByWgQRIwMIEEJgFLfTmzZtbuJTuKRrF3D117dfSevXqSaVKlfzmYwYSIAESAIEVK1Yo51JPPfWU/Pnnn4QSQwIU8xjCt9KlDx06pN6y4ZuZiQRIgATMEti2bZtkyJBBKlSoIEePHjV7GPOFmQDFPMxA7Xq6IUOGqDfsU6dO2dUElpsESCBGBI4dO6YmzhYsWFB27NgRo1K4+7IUc3fXf5z1cN+KdaRMJEACJBAMgWvXrknFihWVC9hVq1YFcwoeEwIBinkI8Jxy6KZNm1QXO51BOKVGaQcJxI5AgwYNJFmyZDJv3rzYFcKFV6aYu7DSjSZ37dpVjXndvHnTuIvfSYAESCBgAi1btlQNhPHjxwd8LA8IjgDFPDhujjoK7ltbt27tKJtoDAmQQGwJ9OjRQwn6+++/H9uCuOTqFHOXVLQ3M5csWaJ+cBzj8kaI20mABIIl8OGHH6rny1tvvRXsKXicSQIUc5OgnJqtWbNmghmoTCRAAiQQCQLTp09Xgv7qq69G4vQ85/8ToJi7+Fa4ePGi+pH17t3bxRRoOgmQQKQJLFu2TD1rMDkOs96Zwk+AYh5+prY54+TJk9UPbPfu3bYpMwtKAiRgTwJbtmyRdOnSKS+TJ06csKcRFi41xdzClRPpotWpU0cqV64c6cvw/CRAAiSgCBw+fFjy5s0rhQsXFjYiwntTUMzDy9M2Z/vpp59Uq3z06NG2KTMLSgIkYH8C8OH+2GOPSZYsWWTt2rX2N8giFlDMLVIR0S7GoEGDJHHixHL69OloX5rXIwESIAF5+umnJXny5LJgwQLSCAMBinkYINrxFCVLlpRGjRrZsegsMwmQgEMIYIY7wqhOmjTJIRbFzgyKeezYx+zKGzZsUD+gOXPmxKwMvDAJkAAJgEC3bt3U8+iDDz4gkBAIUMxDgGfXQzt16iQZM2aUW7du2dUElpsESMBBBIYOHaoEHcLOFBwBinlw3Gx91IMPPiht2rSxtQ0sPAmQgLMITJs2TQk6/LozBU6AYh44M1sfsXDhQvWDWb16ta3tYOFJgAScR+DLL79UzyeEY75x44bzDIygRRTzCMK14qmbNGkihQoVsmLRWCYSIAESkM2bN0uaNGmkatWqXG0TwP1AMQ8Alt2znj9/Xr319unTx+6msPwkQAIOJnDo0CHJnTu3FCtWTPbt2+dgS8NnGsU8fCwtf6YJEyYoMd+zZ4/ly8oCkgAJuJvApUuXpHz58pI1a1ZZv369u2GYsJ5ibgKSU7LUrFlTqlSp4hRzaAcJkIALCNSrV09SpkwpixcvdoG1wZtIMQ+ena2OPHDggGqVjxkzxlblZmFJgARIoEWLFur5NWXKFMLwQoBi7gWM0zYPGDBAkiRJImfOnHGaabSHBEjABQS6du2qBH3YsGEusDZwEynmgTOz5RElSpSQ5557zpZlZ6FJgARIAATgJQ7uX3v06EEgBgIUcwMQJ3799ttv1Q9g7ty5TjSPNpEACbiIwCeffKKeZ2+88YaLrPZvKsXcPyPb52jfvr3A69udO3dsbwsNIAESIIElS5YoQUdvI91S/+9+oJg7/Hfx999/Kz/sbdu2dbilNI8ESMBNBDZu3CipUqWSatWqyblz59xkukdbKeYesThn4/z589Ub7Jo1a5xjFC0hARIgARH5+eef5ZFHHhGEdD548KCrmVDMHV79L7zwghQuXNjhVtI8EiABtxK4ePGilClTRnLkyCForbs1UcwdXPNnz55VrfK+ffs62EqaRgIkQAIiderUUd3uS5cudSUOirmDq33cuHFKzPfu3etgK2kaCZAACfyPQLNmzdQz79NPP3UdEoq5g6scE0MQeYiJBEiABNxCoEuXLkrQR4wY4RaTlZ0Uc4dWN1rjcK4wduxYh1pIs0iABEjAM4FBgwap51+vXr08Z3DgVoq5AysVJvXr10+SJk0qGDdnIgESIAG3EZg0aZISdLcsy6WYO/QOL1q0qDRu3Nih1tEsEiABEvBPYNGiRUrQsaoHPjecnCjmDqzd1atXqxt43rx5DrSOJpEACZCAeQIbNmyQ++67TxAC+vz58+YPtFlOirnNKsxMcdGtlClTJse/iZphwTwkQAIkAIcy2bNnl9KlS8tPP/3kSCAUc4dVK/wUZ8yYUdq1a+cwy2gOCZAACQRPAK3yUqVKSa5cuWTz5s3Bn8iiR1LMLVoxwRZrzpw5qot97dq1wZ6Cx5EACZBAzAkcPXpU1q1b57McZvIYT1CrVi1JmzatLFu2zLjL1t8p5rauvoSFRxShIkWKJNzBLSRAAiRgEwKXLl1S7lmxvNZXKlasmGq86PNMmzZNOnbsqP7w2VNq0qSJOm7mzJmedttym29StjTJvYU+deqUukGxLM1s2rVrl1rG1qBBA2nRooXgTVefEAsd58N+/DfuR17kwXmYSIAESCAcBJo3by6VK1dOINT6c0OwjXnwfBo5cmRcNoi5t2cTjsfLwqhRo+Ly2/kDxdzOtWco++jRo9XNuW/fPsMez1+1mxk/HPhvx59erPFDSJ06tXrDxT7kw3ftx4G3Z2yDmC9evFjl83wlbiUBEiABcwTwLMFkNfz31jLHMwfPImMebMeflozfte34f/z4calYsaK6RrTiV2g9CbBL+4Ot4UgU83BQtMg5qlSpIk888YSp0uBHoBdmTwfhJtO/5SIP3oQh4Eg4hybs+I68EHgmEiABEgiGABoTadKkUYIMIfYk5njG+MqD5xPyaI0NT+XAmvMhQ4bIDz/8IBMmTFDXad++vaesYd0Ge/Cc1F4y8F//DA3lYhTzUOhZ6FjcELhREFzFTMIbor+3UYi9ccwJPxS9mEPQtYSWPsVco8H/JEACgRJAY0F7LnkT8/r168f1AnrKg2cQBNNX4wI+OBYsWBBXPHzG8xNj6ZFKWlkj9YykmEeq5qJ83t69e8s999wj586d83tl3Ey4cfECgM+YMarvXtdOgB8VYgRrb45aax43pZYg4EuWLBFEKcKPh4kESIAEgiGA5wcaGVrSxE/7jv9oXCCPJoie8ujze/qMYUj4bv/nn3/i7cZzMHny5CqUKmKkhzvheRquLnVPZaOYe6Jiw22FChWS559/3lTJtR+ANiaOt2G0wtFNr/1ItBPhBoTwFy9eXN2ImrBr+/Ef2zy9DOjz8DMJkAAJeCOAZwieQfrniPac0o7RuuD1zyBjHi2vr//Dhg2TPXv2eMyyf/9+yZo1q5QrV04OHTrkMU+wG9GjoPVqBnsOX8dRzH3Rscm+r7/+Wgnu0KFDTZVY+wFoY0s4CCKuHw/HNvxoIOLadvzYMOPdKPimLspMJEACJOCFAIQO4+BoUGh/ePagIYHv6AE0k8fL6eM2b9q0SRCAxVdC72aJEiUkT548smXLFl9ZA9qHVjlswaog7Q/P4nAlinm4SMbwPG+88YakT59ejZcPHDhQ1q9f77M0mpgbRVnbjoOxD13s2vgVtuHNGF1cWKbGRAIkQALhIoBeQjxr9H9obEDMsQ37zeTxV54PPvhAfvnlF3/ZlCvsGjVqqOfqypUr/eb3lwHPTtgCm/Q26nsZ/J3D336KuT9CFt9//fp1yZAhg7z55puqpEeOHJGpU6fK4MGD48a6jSZoN5YvMdcLu/54b9v1efiZBEiABEIlYOZZYyaPVg50oQe6pvzFF1+URIkSyezZs7XTBPUf840g5pFMkT17JEvOcysCs2bNUjcJbmp9OnDggKDbHTfh7du39bvUZ0/LzvDGqE1A0X4kRsGPxk2ZoLDcQAIk4DoC2jPIl+Fm8mjHz5gxQ77//nvtq+n/WLIGIR47dqzpY4wZ9c9W475wfaeYh4tkjM7TsGFDQexybwnxfNG1dOLEiXhZtJnpmIWOWZz4jzErdGVpCcKOMR7sR3cQZq2j6x3jV0wkQAIkYBcC//77r7z99tty9erVoIr83nvvKUHv379/UMdj3lGkn5sU86CqxhoHwYMR3hhxo/lKcIyAGxmtdX2CoGsz2fEf3/UJ3fEY49Hn0Yu9Pi8/kwAJkIBVCSDsKTxkhpLgwwPP206dOgV8Gk8+OwI+iZ8DKOZ+AFl5N9Zl4ubCWJC/BCHv0qWLqbz+zsX9JEACJGAnApjE9tVXX4VcZDibwTO3WbNmps+FoUp0s6NxFMlEMY8k3Qif+/HHH5dq1aqZvsrBgwflrbfeEkySYyIBEiABtxD45JNPvK4tD5QBwkvDQVe9evXk8uXLgR4esfwU84ihjeyJt23bpt4QP/7444AutH37dsG4z5UrVwI6jplJgARIwK4E4PHt7NmzYSv+3r175aGHHpLHHnvMMo0jinnYqje6J+rRo4ckS5ZMfvvtt4AvvHz5csGbKhMJkAAJuIFAt27d5NatW2E19cyZM2rycf78+dU4etWqVZVv940bN4b1OmZPRjE3S8pi+XADvfDCC0GXCi16zFJnIgESIAEnE4CIQ8wjkbDsN1u2bKqXFGPp+MO69B9//DESl/N5Toq5TzzW3ImWNW6azz//POgCnj59Wrp27UrXrEET5IEkQAJ2IIDlaL169VJFvXnzpvzxxx+CVjXmDmEe0Y4dO9T68zVr1siyZctUNDX470Dv5ZgxYwS+3AcMGCDvvvuumkTctm1befXVV+Wll16SZ555RhInThxPzPFshifOaCeKebSJh+F6LVu2VOM1WDsZSsKNi9mZTCRAAiQQCwI3btxQ4nrq1CkV2AQRzTAfaMOGDfLNN9/I0qVLZf78+TJ9+nSZOHGi8uAGvxnwbf7OO++o7m24s8YSWgSagv/2mjVrSqVKlaRs2bKqGzxXrlySKlUq5SkzZcqUkiRJkgTiq7Wq/f1Hq/u+++6TdOnSycMPP6z8t2Ob8TiIf7QTxTzaxEO8Ht4yH3jgAYFXolATup8w9h7OiSGhlonHkwAJxI6AXlzhwxzRxeCnAkNyK1asUL4o5syZo5xLYahuxIgRKpwoQjDDlwWeS61atZKmTZtKo0aN1Izv6tWrS4UKFaRUqVKC6I45c+ZUjRE8x1KkSCF33313AjE0iqOn7zgOx+uFFQ60IOLwjVGrVi0VRwIuWV955RVBixqredDCRsv5ww8/VPEs4P4aNsHPBpawwVYEWMEkNzA4efKk/P7773Lt2rUEYVNRU507d05QfqNPj2jUKMU8GpTDeA28oeLGDtd4N7rsFy5cGMYS8lQkQALhIgBxRWxttFw1cd28ebN46hKGu1F/XcJ16tQRTNR69NFHVUREzL2BV8cHH3xQhSDFpFpPwmlmG2KBexPW2rVrxwkruqjNCiuCRmnCipCk/oQ1XNwDPQ96CypWrKh6B8L1bA60DBTzQInFOD+6kTT/6eEoChwaYHLI33//HY7T8Rwk4GgCRnHdvXu3aOIKpyTGLuEhQ4YE1CWMsJuIp43gSaF0Cd97772qBy9LliySO3duKVKkSFyL1ZuwYlxZa7Gi1W1ssXoT1r/++stji9XRN4IFjaOYW7BSvBUJEzbwhhysf2Bv5508ebKaBOJtP7eTgFUJ+BLXL7/8Uokr4g6MHz8+rku4T58+pruEMd6K9cShdAlDWNOmTavOg/MVLlxYypQpo8Z1IayYRIWuYLRY27Vrp7qCvQkr4iOgKxjCunXrVtUVrG+xUliteqdGvlwU88gzDtsVhg8frsQ83OMxmzZtkpkzZ4atnDyRewlo4oruUHQL61uuenFFyw9jltosYYxlGmcJe+sSzpQpU9BdwuhGRkChzJkzq7FbjOGWLl1a4E1RP8ZqFNb3339flRflRnwCjLF6E1Z0iWOMFcIa6iRV995JtDxQAhTzQInFMD+8DWEySbgTHjzwHczkPAKId48xV7244uUNY64QV6xmQMtVL66YFIlgEq1bt/Y5S1jfJXz//fcHPEsYLjERgALi/Mgjj0jBggXVJCkIK2YkY0gJvhT0k5fQYvUmrF9//XVcixWzotFipbA6756mRZ4JUMw9c4nYAPogLAAABKtJREFUVrzV6yeTYPJJixYt/K73xoxSHIfuwkgkRF6DqDNFloBeXH/++WfVcjUrrq+//rq8/PLLXmcJG7uEPS2Z0d97+s9JkyZVy3cwEQr3ZIECBaRkyZJqUk+NGjXk6aefVpN7cK+2adNGrbfVhBUzmrUW69y5c1WL1Zuw4sWCLdbI3mM8uzsJUMyjXO9YD4kJbN9++636g7ijdYK44b4SJqlh7O38+fO+sgW9b9KkSYLWjNsSxBUvMWi56sV19erVCVquGOZAt7DWcoW4YgnOs88+K+HsEsY6WLR0M2bMKNmzZxfMOIawYnkPemaeeuopady4sWo1o/WMaHj65TaehBXrdjHGijr+9ddfVYuVwuq2u532OpkAxTzKtQshN3Zp79q1S7W6vcUKx9gj1mZikkyk0qJFi8K23C2UMhrFFWzQctWLKzhBsPTi2rFjRzGKK9aaao4jgu0ShncnzCrG7GK4bYSwlihRQgVYQMQ6RE567rnnVEhECCvWnPbs2VOJPsqHGMjarOAvvvhC0GL1JqywnWOsodw9PJYE3EuAYh7lukfXJpwTGBOExyjyO3fuVMKhdYc2aNDAeFjYvmMMFd6WjEkT1xMnTqiWq15ckR9jrnpxxUx7tFz14tqwYUPVctXEFbN5g+kS1rwvpU+fXi3fyZcvn1orizWzTzzxhDz55JOqCxpd0fAKhXFflAVlwvpbrMOdMmVK3OQlTVjhcUprscLNLVqsFFbjncDvJEACViZAMY9i7aBrHcKMtd3GBKHDnz7BJaEm5Np/OHhBt7BeXL///nvVctWLK1qEaBnqxVXzzKQXVyyRgbhi+Q2Wz6DL34zjCL33JayLzZs3rxo+KF++vHJKUbduXdX9DGFFixniDveLGJsfOnSo8nkMYZ09e3ac5yVtuY0nYdVz4WcSIAESIIH4BCjm8XlE9NvIkSPVGKini0DIIXhagutATcDN/PfkfalcuXJqLB7juRBwjO9C0Dt06CDdu3dXzizg1GL06NEqqMBnn30m6G6H20a9S0OMsaLFigAFaLEykQAJkAAJWIsAxTyK9YGlNvjzlNAihtjrE1q7RiGH+GK5jdYVrM/PzyRAAiRAAu4kQDGPYr1jZrJRsHF5jDlDtI8ePRqvNOiC1os5WthMJEACJEACJGAkQDE3EonQd4yTQ5gxbq5PEHB4pNJ3sev3Hzt2TIk9XDgykQAJkAAJkIAnAhRzT1QisE2b/KadGuIOz1sQcoyXe5oUp+XlfxIgARIgARLwRYBi7otOGPdh2Rla5nAOAw9b+Ixud+NytDBekqciARIgARJwCQGKeZQqGuuzNa9v+G8cH49SMXgZEiABEiABBxKgmDuwUmkSCZAACZCAuwhQzN1V37SWBEiABEjAgQQo5g6sVJpEAiRAAiTgLgIUc3fVN60lARIgARJwIAGKuQMrlSaRAAmQAAm4iwDF3F31TWtJgARIgAQcSIBi7sBKpUkkQAIkQALuIkAxd1d901oSIAESIAEHEqCYO7BSaRIJkAAJkIC7CFDM3VXftJYESIAESMCBBCjmDqxUmkQCJEACJOAuAhRzd9U3rSUBEiABEnAggf8DZWmVo/7F6XMAAAAASUVORK5CYII=[/img]
In triangle ABC, angle A is 35º and angle B is 20º.
Select [b]all [/b]triangles which are similar to triangle ABC.
Decide whether triangles ABC and DEC are similar. Explain or show your reasoning.
Lin is trying to convince Andre that all circles are similar.
Help her write a valid justification for why all circles are similar.
Must these parallelograms be similar?
[table][tr][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAO8AAACBCAYAAAAoju2TAAAQA0lEQVR4Ae2daagP3x/HZcm1XfuW5CL7mpBICMkjbh54QNxCCNl3IiGkkDxTtrJneaB0U5QinqgrdcuDy+Xa931t/r3n9/98zZ07+/adc+d9app753tm5nNe83mfzzlnZs7U0ZhIgASUJFBHSatpNAmQgEbx0glIQFECFK+iF45mkwDFSx8gAUUJULyKXjiaTQIUL32ABBQlQPEqeuFoNglQvPQBElCUAMWr6IWj2SRA8dIHSEBRAhSvoheOZpMAxUsfIAFFCVC8il44mk0CFC99gAQUJUDxKnrhaDYJULz0ARJQlADFq+iFo9kkQPHSB6oRuHjxorZ169ZqS7UM/Cc1BJQV75YtW6o52P79+7UbN25o9+7dSw1clQzZt2+f1qJFC61OnTo1FpXKkTZbKyoqtGXLlmljx47VioqK9AV/Y1tYX1VSvABi5WSyDXDCgkmbE8Rpz+zZs3WeXbp00Y4cOaKBryRyFBL+1u/fv9dKSkqq+Wnz5s01LOKnY8aM8XdQU24lxYumHQAMGjRIu379em5BNIYD4jdEEQBkciZgZElezqy8/gqOgwcP1v1QKkTjvvgdlSR8N0xSUrwQKQSKtTkBjAgYgJicCQgrRlhnTn5+RVCR4BJnhaikeNHcABy7mmvp0qW24vZzEWp7XvADxylTptT2oiZWPgksYZvEXgxWUrzSb7Cr1eCMcEpGXmcXEEfDYBVTeALGsRi7wBL+LP+OoJx40byDMNHcs0r4Hf1dCNxO3Fb7ZXGbsQUDbhhgQV8N/DDoh1tGZOjdM1AJJtmSUU68iKYAhBFSSXAw3CaCs4lwMRDD5ExAxCtOhwoRrRZsl74wxEwBO3OUX6Wvm1SLTznxSn8WAjYviLb43XirQ8ByXZOACBQczQ4HwcotJGNFWfMo3CIExB+TquyUE6/UbhAp+mxYEC3EEdHco3jFnZzX4mxgaJXghDK+YPU7t/0jIN05ME0qJXemiEokDmd1OGn+4UkWJncCUuE5VXbStE5iAMbd4vTmkJF7BJekklLiFUBwKLskkZl9XjtC/7aLMCnef0yC/iW+mWTgUEq8ElnRZLZL4pB2TUG7/bK4XcYPzP1dIwvhiWYhkz0BES+bzTaMZADFydmkKcjIawPRsFn6aRhRtkqIyHBG9HuZ3AlIl87JP92P4j2HUpFXhGnXzAM0cbakRvy8o05nTnmgBfd4jczAWJ7PZSvG27WT4IKms5Glt73951JGvIAhwjQXE00W4xscSdV8ZjtU/B9cZZxAHs7AiL1EEd4m8n5VwVJG5yHgo0eP5l5TxXMIeG116tSp3g/oklMZ8Rr7FOJY5jXAUbguV9zmZ4wniIjBFX1dsrSB5bAZXREjR7OP4v+oUnRHisoim+PAkeBQVguadfg9iaaKjXncTALVCGDMBX6JlgsW8VG7Ll+1nT3+o4x4PZaH2UggMwQo3sxcaha0thGgeGvbFWV5MkNAefGWl5drP3/+zMwFY0HVInD//v3YDFZWvDt37szdzsAI3qxZs7SHDx/GBooHJgGvBL5+/aqtWLGimn8uX75c+/z5s9dDeMqnpHjlZrh5GL5jx47ax48fPRWcmUggLgKjR4+uJlzx01GjRkV6SuXEW1ZWZglGAOGFfCYSyBeBc+fOOfrn6dOnIzNNOfHu2rXLEY6ImOuakxWQSf6ZTJ8+Pbvi3b59O8VrMYsIhZl/YXq5BtOmTcuueO/eveso3rVr10YGhwciAb8Ejh8/7uifUT5yqlyzGTCLi4stATVp0kSrqqryy5v5SSBSAnbPNg8YMCDS8ygp3jt37tQQb+/evbXbt29HCocHI4EgBGSSA2MzesaMGdqjR4+CHM52HyXF261bN128GzZs0F+5qqystC0gfyCBJAn8/ftXq1u3ru6f6MKVlpZqb968icUE5cRr7PP++fMnFig8KAkEJbBp0yZduA0aNAh6CM/7KSferl276nAAiYkE0kTg9+/fWr169XT/TOJ5A6XEe+vWLR0M+hIAxUQCaSKwceNG3T8LCgoSMUsp8Xbv3l2Hg74uEwmkicCvX7+0+vXrJxZ1UXZlxHvz5s1c1OVbRGlyW9oCAuvXr9f9s3HjxokBUUa8PXr00OEAEhMJpIkAggkGqNCdS6KvK2VXQrzGyed+/PghtnNNAqkgsG7dOl24TZs2TdQeJcTbq1cvHQ4ffUzUN3gyDwS+f/+uNWzYMPGoC9NSL95r167pYNAk+fbtmweczEICyRFAQIFvFhYWJnfS/58p9eLt06ePDmfNmjWJw+EJScCJAIIJbgsl3dcVmyIRL+aixWzwy5Yt0zDbPtaYLT5sunr1ai7qYmoRJhJIE4HVq1fr/okvTTglTMQOfeCrHtAHBrUuXbrktIun30KJF5OcQ6ioeawWfPIhzNfl+vXrpx931apVngrDTCSQFIEvX75ojRo10v3TboQZQc346RizRvAtqDAfCgglXswCD4PwFQPMEC+GQLDyAaug3yu9cuVKrkIAKCYSSBMBBBT4fqtWrWzNgi6QB3Ou4Y6JJPwtrw1C3EFTKPFCrE4vF8tX/YJ8bnPgwIF6wVeuXBm0bNyPBGIhgFkg8TAGhGkXdXFiRF6jaI3GQDvyUbKgn0AJJV6jMVZ/S2TG2k+6fPmyDgZwPn365GdX5iWB2AnItK5t2rQJdS6JzHYCdzt4KsUr34UFJCYSSBMBTC2MGVvcoq4Xm1MtXun3+qlZLly4kIu6nIPZiwswT5IEJOq2b98+9GmlW5m6ZjMGrVA7wUA/aciQIfp+GMVmIoE0Efjw4YOGRyCjiLoYK8JxMJgVNMXWbJbRND+DVWfPntULhELJyHXQgnE/EoiaAAZP4Zv4MkeYBN/GvWEcK8yt1FjEK58j8VurDB06VC8QJvBiIoE0EYDgmjVrpvun0wizm804jozpON2pcTsOfo9cvCJcdMb9pFOnTulgUBu9e/fOz67MSwKxE5D7up06dQp1Lhmk8hvYrE4aqXhFuGgy+232Dh8+XBfvkiVLrOzkNhLIG4G3b9/qLx4gsGzbti2wHaKPKIQLIyITrxgWRLgnTpzIRd24pskMTJw7Zp6APMPcuXPnwCxEH1EJF4ZEIl4xLIhwYcSIESN08S5evDgwHO5IAnEQQDCRJ6HwnawgSfQRpXBhR2jxhjUMbx+hOYLl9evXQdhwHxKIjQBeRYVv+r3lKQaF1Yccx2odSrxiGEbPbty44bjY9YFHjhypw1m0aJGVfdxGAnkj8OrVq9wtnZ07d/q2w48+fB88bOSViOllbfWU1bFjx3JRF6CYSCBNBGSWDEz07zfB373oQvL4PT7yh4q8GPb2uljdjB49erRewIULFwaxnfuQQGwEXr58qbVs2VL3T3zQ3W+Cv3vVBvIFSaHEG+SEso9xhPnFixeymWsSSAUBmRESE/2nNeVNvKht0GRYsGBBWtnQrowSeP78uda6dWvdP/fs2ZNaCnkR78mTJ3UwEC9AMZFAmgjI1w969uyZJrNq2JIX8Y4bN04X7/z582sYxA0kkE8Cz5490/CSPQLL3r1782mK67kTF+/p06dzUbeqqsrVQGYggSQJ4CN2EG7v3r2TPG2gcyUu3vHjx+tw5s2bF8hg7kQCcRFAMGnbtq3un/v27YvrNJEdN1HxGt/Xffr0aWSF4IFIIAoC8lX7vn37RnG42I+RqHgnTpyo12pz586NvWA8AQn4IfDkyROtXbt2un8eOHDAz655y5uYeM+fP6+DQX+isrIybwXmiUnAisDmzZt1/+zfv7/Vz6nclph4J02apMOZM2dOKkHQqOwSQNTFhHIILAcPHlQGRKziRb/2zJkz2u7du3NR9/Hjx8rAoaG1m0B5ebmGJ/3weC6Ei4n+VUqxiBev9skbFYAiC0aamUgg3wTKysq0YcOG5fxS/BMv3auUYhGvNJEFinH94MEDlfjQ1lpIAE9OGX1S/u7QoYP28+dPZUocuXhv375tCUYAYSJ2vC7FhQzy4QPywoH4o3mtykgzapjIxbtjxw5H8Zph8f9/3QqyyD+LyZMnZzfyHjp0iOI19PMpyPwL0s81mDlzZnbFi9FkJ1iIzEwkkC8CpaWljv557ty5fJnm+7yRN5thgUyVaRYxXmxWaUDAN03uoASB4uJiSwFPmDBBCfvFyFjEi4MfPnw497hZQUGBhg+HcU5mwc51vgng2QP5XlBhYWGoydTzVZbYxCsFsps1Un7nmgTySQBzVamaYhevqmBoNwmknQDFm/YrRPtIwIYAxWsDhptJIO0EEhFvRUWFNnbsWH1JOxDaV/sJYOZS8UdZ45u7+PSOSmM0iYjX+JICHoljCkYAH2MuKSnRioqKcrc68KkZJu8EEEjMtzCN/2MEOuxHr71bEy5n7OKFWI1wKF7/FwzRABFCOCJy4BlxrPFlRibvBC5evKhzBD9jgl8ag4wKAo5dvDK5+pYtW3RoWDN5JwDhIrpCuHAulZp13kuZXE43P8TEc2CNCJx21rGKV6IunE7+pnj9Oao4GxgyhScgwcSpBYjPeULAaY++sYpXIKCfIeIFPCZvBFDzIwLg485pjwLeSpT/XNL1cOKpSoUZm3hRa0lTD5cMsPA/xevdgYXh0qVLve/EnLYE8OU++KDbOIGIN+2+Got4JWIAFKKuJPyPhckbAYgWvIzNN7Rg8CFzq0+mejtqdnNJZejWBZF+bybFKzWXOWJIMzq77uOv5HAeiBeCBVN5kF4qQdwywugpkzcCEC3YuX0Nwc5/vZ0luVyRh0GJulb9NKMzJldEdc8kvKZOnar3e1EZQsgQrERlEbe6pUzOcjSXwcut1SIih4jTnCIXrxQcUUKeXpG1RA44IJM7AWmpwOmsBlikGYgIzOROQFosbjkReJA37a2aSMXr9vSKwEt7jeZ2cZP6XcTr5EQSTYxjC0nZp9J5EDDgf279WLBGPrBPe4pUvHhqBQW361PIQIC5L5x2SPmyT5rNTsKUPGzNOF8lL76H1o08eqpCgIlMvFKzOdVYkset9nO+DNn5VSpDJ2FSvN78QVjatWIgXDw3juDjdivJ2xnjzxWZeMWJjLc1zObLfTY+TG8mY/2/9GmdogCbzdbszFulC2LVioFfyiOo6O+6DWiZj52v/yMRr59+Amo2LEzuBBAN4EwY6LNyOhG3U2vH/Sy1Pwc4it/hHjkWvP6H1wDNL3wgryopEhVJrWbXJDHCkJE8lSAZ7U/6bxEoBCzvmyIy7N+/P3ff16lZnbS9aTyfBBcRsHmN1otTizGNZYJNocWLiIBmnd0glbnggIT8VpHEnJf//0dABGx2OlSEKjpd0tcVlRt8zriAG7ar7IehxZv0hcjq+eBkqCDFAeF8bL1k1Rv+KzfFm+3rz9IrTIDiVfji0fRsE6B4s339WXqFCVC8Cl88mp5tAhRvtq8/S68wAYpX4YtH07NNgOLN9vVn6RUmQPEqfPFoerYJULzZvv4svcIE/geaHB8IMHN7OwAAAABJRU5ErkJggg==[/img][/td][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAV8AAACXCAYAAACyeVjsAAAUWUlEQVR4Ae2dO2wdxf/FzSsgXjYhiISXHYiEoLEFEuJR2JQICRe0KDbiIRpkiwJBgWwBFY3TUCAKh1d4hMQmQERn09BAZEVISIjCDSAFIZkmDQX717m/nPv/er2v2d27d3fmjHS19+7O7s589jtnzs7OvXckUhIBERABEWicwEjjZ9QJRUAEREAEIomvgkAEREAEhkBA4jsE6DqlCIiACEh8FQMiIAIiMAQCEt8hQNcpRUAEREDiqxgQAUNga2srWl5ejubn53vL48ePRzs7OyaH3opAPQSCEN+NjY1oc3MzlxjzqbHlovIuA675zMxMNDIysuc1NjYWra6ueldnVciNAPUhb6/t7e2e3qAjz0pBiO/4+HivQa2traWyWFpa6uWZnJyU00ml5O8GXHcIL2IFQouGhtfc3FxfjLPix18yqhkJUEcQF2kJnTg6a8TSyspKWrbe+iDEl8KKhpSU0KgAa3R0NEKvpRQWATQSCm/SXQ/EGNsnJibCAqPa7iLAjhh6kpZmZ2d7sTI9PZ2Wpb8+CPGFoKLxoEeKNy5sY0+V1aP1iemNdwToerOGFtiosvJ4B0YV2kWAnXCasFoTF9eZXQe69CEI8UVdAQwCbBsPAE1NTfXW590iJMHTOj8IIC7wyrrrYcNKu3vyg4RqkUWAJg6xEk/QEpq4osNTe48SP6onn9lrwcEw8TZCDYpEwlxSfLNqj4cnyIfOWilcArxLit8l887I6ksepWDEFyAwposGhF6K43x6wJYXIv5vp/hmOV+KL/IqhUtgYWFhz50y74qgL0WGG0gvqEii08UcTjQiPWBjGIS9pJuxQ1JxInxoK/GNkwnrM4WWDhdiiwexiIuiww0kFpT4WvcCWPFbB0LRMiwCFFY0oqS5mbxLQsxIfMOKjXhtIbaIAYzvItEJU4zj+bM+ByW+BAd4GufNCovwttH9IjbwZQt8y21xcbHvatjIJL7hxUa8xowVdsqY/+sy3MDjBSW+nPGABqQ5mwwBLUkADpjPBRAjeMHR4A4JL3xGw1MKm4DtiBETZe+ggxFf3lqiMbHnSrrFDDusVHsQgIuJxwZdju6YFCPsiCG8EOKyKQjx5SA5bw8oxGpIZcMmvP34sBYirBQ2ATvft8xwA+l5L74AxcnPdDNYotfioDlhaCkCSQTss4IqjS3p2FrXPQL8zkDaN92K1sh78eUQQ9yx8EcyXKeHFAWrfP4QwFAVOmvdKflzTavUhGO+VYYccH6vxZe3iknTQAhQDapKGPq9L1yunRMu1+v39S5aOz64z5oXXuRY3oovbw04zhuHwaEHOBo1qjid8D7jzujYsWO932HF0k4zwwwIDlmFR0Y1jhOAZuCV9Y3I+D5Jn70UXzSU+DhvUuU59FC1B0s6ttZ1iwDdDBsWlhBd3Bmpc+7WtRxkaTnTAbFRNXknvmgoRX+pjEMPmFSvFDYBdNgY/8dMGDSwsnM3w6bof+055bDqwzaQ8k58cStQtPFAqIvm9T+sVEMREIE8AtSXqkMOOI934psHT9tFQAREoA0EJL5tuAoqgwiIQHAEJL7BXXJVWAREoA0EghPfv//+Ozpz5kz0448/toG/yiACItBRAufOnYvW19ejv/76q1QNghHfCxcuRM8991xvfp6dTvTRRx+VAqedREAEwiTw6aefRpdffvkuLTl69Gj0+++/OwEJRnwfeuihXbCsAH/yySdO0JRZBEQgTAInT55M1RHXnxsNQnzhbq3YJr0PM5RUaxEQARcC+/bty9SS999/v/DhghDfJ554IhNYkhhr3f++QikO4qAYKB4Djz/+uMTXEnj44Yclvpe+j66GVLwhiZVYucYAvl1bNAXhfF977bVc8X399dd7/9uF/+7SSwwUA4qBeAy88cYbuTqCH2QqmoIQ319//TUT2ksvvVSUl/KJgAgETIC/B5PmiM+fP1+YThDiCxovv/xyogA/9thj+tWqwuGijCIQNoGLFy9Ghw4dStSSt956ywlOMOL74osv9oAdPHgweuSRR6Inn3wyOnHihBMsZRYBEQibwE8//dQXXjxLwuvVV1+NfvnlF2cwQYivBfbee+85Q9IOIiACIgACNHF33313ZSBBiC+BPfjgg5WB6QAiIAJhErAm7sMPP6wMwXvxtcDkeivHiw4gAsESoIm75557amHgvfgSmFxvLfGig4hAkASsiavr92C8Fl8LTK43yDajSotALQRo4upyvSiU1+JLYHK9tcSfDiICQRKwJq4u1wuQ3oqvBSbXG2SbUaVFoBYCNHFHjhyp5Xg8iLfiS2ByvbzUWoqACLgSsCbu448/dt09M7+X4muByfVmXn9tFAERyCBAE1e368UpvRRfApPrzYgqbRIBEcgkYE3cIP5wwTvxtcDkejNjSxtFQAQyCNDE1TnDwZ7OO/ElMLlee5n1XgREwIWANXGD+g0Yr8TXApPrdQk15RUBEbAEaOIOHz5sV9f63ivxJTC53lpjRAcTgaAIWBOHfyoeVPJGfC0wud5BhYuOKwL+E6CJm5iYGGhlvRFfApPrHWi86OAi4DUBa+IG6XoB0QvxtcDker1uG6qcCAyUAE3c+Pj4QM+Dg3shvgQm1zvweNEJRMBbAtbEffbZZwOvZ+fF1wKT6x14vOgEIuAtAZq4u+66q5E6dl58CUyut5F40UlEwEsC1sR9/vnnjdSx0+Jrgcn1NhIvOokIeEmAJu7OO+9srH6dFl8Ck+ttLF50IhHwjoA1cV988UVj9eus+Fpgcr2NxYtOJALeEaCJu+OOOxqtW2fFl8DkehuNF51MBLwiYE3cyZMnG61bJ8XXApPrbTRedDIR8IoATdztt9/eeL1qF9/t7e1oeXk5mpqaikZGRvqvmZmZ6NixY9HOzk7lShKYXG9llDqACARLwJq4LNcLTYN2QcPimgatK6tptYkvCrC4uLircPiWyPT0dDQ6OtpfD1EuW1hEiQUm1xtsu1HFRaAyAZq42267LfFY0CmIqxXcJE3Db0BAoF1TbeKLE09OTkYo3MrKyh6B3djY6Ivw3Nycazn7+QlMrrePRG9EQAQcCVgT9+WXX6buTfOYpmnQO4gzXLFrqlV80VNkudq1tbV+L+JaUOS3wOR6yxDUPiIgAiBAE3fo0KFMIHmaBlNJZ+zqfmsV38xaXNrIgqLQronA5HpdySm/CIgACVgTd+rUKa4uvSyraY2K79bWVr+XcK2pBSbX60pP+UVABEiAJu7gwYNcVXoJt0vxbbXzXVhY6BUU4yiuicDkel3JKb8IiAAJWBN3+vRpri69XFpa6mkaxn5dUyPO1z41xMwHOGCXZIHJ9bqQU14REAFLgCbu1ltvtaud38c1rcww6kDEd3V1tff0D08AOd8XootZDq7WHFQITK7XOUa0gwiIwCUC1sTh4b9Lsppm5/tC01zNJM87EPGlFedYCJYQYcwDdu0hLDC5Xl42LUVABFwJ0MTdcsstrrtGSZqG+b1lNI0nH4j4wt1CZPlCLzM7O9sfmEZFiiYCk+stSkz5REAE4gSsiXN1vThWkqbB9dJgQoRd00DEN60QEGMWtogDtsDketOoar0IiEAeAZq4AwcO5GV12o4hB36D11XUGxVf1IoOGDMf8hKByfXmkdJ2ERCBNALWxK2vr6dlK72es7igbS6pcfHl2EnedDMLTK7X5ZIqrwiIgCVAE3fzzTfb1bW9L6pp8RM2Lr4cJ8nrJQhMrjd+yfRZBESgKAFr4r766quiuznl64T4Ym7c2NhYb9wXP1SRliwwud40SlovAiKQR4Ambv/+/XlZS22HpmHWA55lZWla0sFrc74YeJ6fn482NzeTztOb+cA5v/g2CAqdlghMrjeNkNaLgAjkEbAm7syZM3nZ92zHpABoWto4MbZT0/DQLUvT9hw8iqLaxNfOZOC8XkxGthOSsR7CmzUp2QKT6026ZFonAiJQhABN3E033VQk+548dWnangNfWlGb+EL18S0QjOXyNy45rQy9AtZje14iMLnePFLaLgIikEbAmrivv/46LVvu+ixNw6QBbHd1vDxpbeLLA1ZZWmByvVVIal8RCJsATRyeMbU1tUp8CUyut63honKJQPsJWBP3zTfftLbArRFfC0yut7XxooKJQOsJ0MRhuLPNqTXiS2ByvW0OF5VNBNpNwJq4NrteUGyF+Fpgcr3tDm6VTgTaTIAm7sYbb2xzMXtla4X4Ephcb+vjRQUUgdYSsCbu22+/bW05WbChi68FJtfLy6KlCIiAKwGauBtuuMF116HkH7r4Ephc71Cuv04qAl4QsCbu7NmznajTUMXXApPr7US8qJAi0EoCNHHXX399K8uXVKihii+ByfUmXRqtEwERKELAmrgujPWyTkMTXwtMrpeXQ0sREAFXAjRx1113neuuQ80/NPElMLneoV5/nVwEOk3Amri2z+uNgx6K+Fpgcr3xS6LPIiACRQnQxF177bVFd2lNvqGIL4HJ9bYmDlQQEegcAWviqvxy2bAq3rj4WmByvcO67DqvCHSfAE3cNddc08nKNC6+BCbX28l4UaFFoBUErIkr8y8VbahEo+Jrgcn1tuHyqwwi0E0CNHFXX311NyvQ9A/rEJhcb2fjRQUXgaETsCZuUP9I3EQlG3O+FphcbxOXVucQAT8J0MTt27ev0xVsTHwJTK630/GiwovAUAlYE5f2r8JDLaDDyRsRXwtMrtfh6iirCIjALgI0cVddddWu9V380Ij4EphcbxdDRGUWgXYQsCZubW2tHYWqUIqBi68FJtdb4UppVxEInABN3JVXXukFiYGLL4HJ9XoRL6qECAyFgDVxp0+fHkoZ6j7pQMXXApPrrfvS6XgiEA4BmrgrrrjCm0rXLr7fffdddPTo0ejee++Njhw5Eo2MjERyvd7EiyoiAo0QuHjxYvTOO+9Ejz76aHT//ff3dARacurUqUbO38RJahXfZ555pg8JoPh64IEHmqiLziECIuABge+//z46cOBAXz+oI1ieOHHCgxr+rwq1ie8HH3yQCIvg3n33XW+gqSIiIAKDI8A7ZmqHXeKnI//777/BnbzBI9cmvocPH84UX0BbXl7WSwwUA4qB1Bh49tlnM3UEQgyj50OqRXz//fffXGC299L7/x+SEQuxUAy4xcDzzz/vg/ZGtYgvSOzfvz9TgC+77LJoZmZGLzFQDCgGUmPgvvvuy9QRdFRvvvmmxNcSeOWVVzKhvfDCCza73ouACIjAHgL//PNPpo5AfM+fP79nvy6uqM35/vnnn9HY2FgiOHwP+7fffusiH5VZBESgYQJwtmlDMZjv60uqTXwB5Oeff46efvrpXeCeeuqpCF+2UBIBERCBogQwOyouwG+//XbR3TuRr1bxZY0vXLgQnT17Nvrjjz+4SksREAERcCZw7ty56IcffnDerws7DER8u1BxlVEEREAEhklA4jtM+jq3CIhAsAQkvsFeelVcBERgmARKie/W1la0ubkZ7ezspJYd25AHr6zEY2GpJAIiIALb29t97aCGpC2Rt6uplPhOT0/3nkRubGyk1ntpaan/tDI1UxRFo6OjvXyrq6tZ2bTNIwK2Y0ajyurEPaq2qlKQwMLCQl874jMe4p+7/I8WAxFfNCY75zeNOQQXMMfHx9OyaL1HBBAXi4uLexoWYmV+fl4i7NG1rlIViC8MXtoLekERDtb5prlV63oBKc0hT05O9iAiv5L/BHi9cbczNzcX4bqjofHuZ2pqSgLsfxhUqiHElsZuZWWl0rGGvXMl55smmmhMeM3OzvbENUl8sQ7CjHy67Rx2GAz+/OyQIcBxt4LrT2FOi6nBl1BnaDsBxAk6aOgGOu+up9rFl0MJaERscEniC3iACOej5D8ButukWEDtIcjIA1ejztj/eChTQ2oGOmofYqSU+BJCkkvheAwaU5r4YhuEF6+4CypzUbRPuwlgJguvd1ZJGVdpw1lZ+2qb3wRo6tBB+6IZpcSXohoXXwJCI0Jivrjb4Xrm8ztsVDsOMeEBSlZiXOhuKItSeNts5x3Xki7TqFV8OW7HnomNCUubeAuqub2Wir/vKb4TExOZlWTnnSfSmQfRRq8IYHiBD9jiOtL1itYmvmxgeMjGlCS+amCkE87SDjNljdVx2EHiG05s5NWUhs7qSt4+XdleSXzt7SEaDMb17G0Bhdb2WBwTtvm6AkvlLE+AjQjzeZMSYwUxJPFNIhTeOnbGvjxgi1/BSuLLRkLXy888CddTfPlZX6ogoXCWvPYQV/yd1PHjx3tfIV1fX+99puhyGQ4Z1TSJADtjDFH6OjxZSnwJhmLLHir+VT82OIov5/1if6XwCCAeeOcDkeULDQyxw2EqPYgNLzZsjSG2HOeNa4rN1/X3pcSXogrx5XhekptlPohuVr6uQ1T53QggLiC0+IYS3jNhGAuCzM6a67UMhwCeCeDBLOLADmv6SKCy+NKtJLlZii9EGg1NDcvHEKqvThwXtoJc39F1pC4QgFZAJ3hX3YUyly1jJfGFo4XjTXK9KBB6MYJEw8LtZdbT7rKV0H7dJ8A7I8SIUpgEeOcDPQlBJyqJL79nnXWbCPEN5TYizCZTT635PMD3W816aPl3FIztQit8fsAWv2qVxJewsnop5OEL7kZJBOIEOHSlO6M4mTA+Qxf4gA2Gbnl5OfPli46UEl8OJ0BUs1wvQofCqyfYYTSkrFpiLJcdNZ5oY7oZpp0hRkJyPFmMQtzG50HUirylL4xKiS8qD9HFK68XKprPF6CqRzqBtEaFhyu+zuVMp6EtJIBOmTqRt+z6b/iyzliWFl97EL0XgSIE0LAgtHhhbBcNSaJbhJzy+EhA4uvjVVWdREAEWk9A4tv6S6QCioAI+EhA4uvjVVWdREAEWk9A4tv6S6QCioAI+EhA4uvjVVWdREAEWk9A4tv6S6QCioAI+EhA4uvjVVWdREAEWk9A4tv6S6QCioAI+Ejg/wB3pw0GVJVjAgAAAABJRU5ErkJggg==[/img][/td][/tr][/table][br][br] Explain your reasoning.
Determine if each statement must be true, could possibly be true, or definitely can't be true. Explain or show your reasoning.
An equilateral triangle and a right triangle are similar.
A right triangle and an isosceles triangle are similar.[br]
Quadrilaterals [math]Q[/math] and [math]P[/math] are similar.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAa4AAAFICAYAAAAI6BoFAAAgAElEQVR4Ae2dCdhN1RrHL5JUhisis0qU+SYUGRPJVGQKRZOITFHXLWTIUKaohAwpUq4puUSpi2QsdDN/hMqUIaGUdZ//2137nu9zzvn2OWfvffbwf5/nPOf79ll7rff9rb3Xfw9r+IuikQAJkAAJkICHCPzFQ77SVRIgARIgARJQFC4eBCRAAiRAAp4iQOHyVHXRWRIgARIgAQoXjwESIAESIAFPEaBweaq66CwJkAAJkACFy8PHwKeffqpWrlzp4QjoOgmQAAnEToDCFTszV+wxdepU9Ze//EU+rnCITpAACZCAQwQoXA6BtrKYlJQUlTNnTlWkSBEKl5VgmRcJkIAnCFC4PFFNqZ2sUaOGKleunOrfvz+FKzUa/kcCJBAAAhQuj1WyFqvNmzdTuDxWd3SXBEjAGgIULms4OpILxArvtSBeMC1ijhTOQkiABEjAJQQoXC6piPTcOHHihCpfvrw8ItRpKVyaBL9JgASCRIDC5ZHafvrpp1WOHDkUOmZoo3BpEvwmARIIEgEKlwdqG+O18IgQXeBDjcIVSoN/kwAJBIUAhcvlNY1HhOj63qRJk0s8pXBdgoQbSIAEAkCAwuXySoZg4W5r/vz5MksGZsrQn4cfflh+0/9D5GgkQAIk4HcCFC6X17CeHcPMNx4p0kiABEjA7wQoXC6vYYhRpM9DDz0kd1z6d95xubwy6R4JkIAlBChclmBMTiZ8x5Uc7iyVBEgguQQoXMnln1DpFK6E8HFnEiABjxKgcHm04uA2usdj3kIaCZAACQSJAIUrSLXNWEmABEjABwQoXD6oRIZAAiRAAkEiQOEKUm0zVhIgARLwAYG4hOvMmTM+CJ0hkEB8BE6fPh3fjtyLBEjAEgIxCdesWbNUxYoVZexQ7ty5Vffu3S1xgpmQgBcIoDMMFvDEYPC8efOqvn37esFt+kgCviNgWrjmzp0rJ2zaGRyaN2/uOygMiATSEpg+fXrY4x+DwGkkQALOEjAtXDVr1gx74kLIJk6cGHF2Bz2rA78jz4BBNu5nc9NNN0U8/nfu3OnsWcvSSCDgBEwLV9asWSOeuGnvwvj/X8jqL8FhMGfOnIA3IwyfBJwlYFq4SpcuHbExbt++vRowYAA/ZODbY+DKK6+MePx/+eWXzp61LI0EAk7AtHCNGDEi7IlbpkyZgCNk+H4lcOrUKdWzZ8+wx71+qnD77bf7NXzGRQKuJWBauBABlo/XJyy+CxQooDZt2uTa4OgYCcRLYMKECeraa681jvd+/fqpJ554wvgfx3/VqlXV9u3b4y2C+5EACcRJICbhQhkHDx5UY8eOlRO4QoUKcRbL3UjAnQSWLFmicBelL9BatGih9u7dazi7b98+WdRzw4YNxjb+QQIk4CyBmIVLu1e0aFE5uY8fP6438ZsEPEtgx44d6sEHHzQECxdly5Yt82w8dJwE/EwgbuHq1q2bnORvvvmmn/kwNp8T+PXXX9Xzzz9vCNbVV1+t8JiQRgIk4F4CcQvX8uXL5WSvX7++e6OjZyQQhQBmwihWrJghWj169FAQMhoJkIC7CcQtXAjrqquukpPe3SHSOxJITeCzzz5TderUMQSrYcOGatu2bakT8T8SIAHXEkhIuFq3bi0n/4IFC1wbIB0jAU0AHYsef/xxQ7BKlCghHS307/wmARLwBoGEhAuT7qL3Fedr80ZlB9nLYcOGqdBBxCNHjgwyDsZOAp4mkJBw/fLLLyJc2bJl8zQEOu9fApiOKXTWF4zFOnHihH8DZmQkEAACCQkX+Nx1110iXmvXrg0ALoboFQIYZ9W4cWPjsWDt2rXVunXrvOI+/SQBEohCIGHhGjdunDQOffr0iVIMfyIBZwgcPXpU1onTA4gxu8u7777rTOEshQRIwBECCQsXZhJAI3HjjTc64jALIYFIBHARhQVOtWgNHDgwUlJuJwES8DCBhIULsetVYVNSUjyMIjbX8Z5k5cqVl3yCxCA2YvalXrx4sapUqZIhWO3atVOHDh2yr0DmTAIkkFQClgiXnnnglVdeSWowThbev39/o6HUV/j6u3z58rKwppP+BLGsb775RukhGWBfpUoVuZAIIgvGTAJBImCJcK1fv14accyWHRRr0qSJxIxviBg+GBZQpEgRQ9CwsjHNegKnT59WmK1dXyigV+vkyZOtL4g5kgAJuJKAJcKFyPLnzy8NydmzZ10ZqNVO5ciRQ+INJ041atSQ32rWrGl1sYHPb8qUKakuDvr27Rt4JgRAAkEjYJlwderUSRrrmTNn+p4h3mPpq/1wwULMov0ebh9ui04ATGvVqmVwbdasmdq1a1f0nfgrCZCALwlYJlwfffSRNCr33XefL0GFBjVv3jyJFXdW4Sw9YQu3D7eFJ7B79271yCOPGIJ1yy23KKyZRSMBEgguAcuECwhxl5ExY0bf09QdM7AidDjjHVc4KrFtwyztQ4YMUVmyZDFEC93daSRAAiRgqXDh8Q3E6+OPP/Y1Wf0OC8tihDN00gAHdNygxU5g9uzZCndW+nFr165dVVDencZOi3uQQPAIWCpc06dPl8YG77v8bLpBDTdmC2Kmfw/XccPPXBKNbc2aNQpLjGh+WOvt66+/TjRb7k8CJOAzApYKFwblotHJly+fzzD9P5zNmzcbDWvoAOQxY8Yo9CLUjS5nzP8/s/T+OnDggNIraoNfwYIF1dy5c9Pbjb+TAAkElIClwgWG1atXl8Z7y5YtvkQaekelRSr0G+O40HmDZo4ABD9XrlyG4GP5ERoJkAAJRCNguXC9/PLL0gihA4MfDR0yIFR4z6UHHuMbgoa7MZo5Alh8tGLFioZgoefgsWPHzO3MVCRAAoEmYLlw7dy5UxqjMmXK+BKsnpeR76/iq96NGzeqFi1aGIJ1xx13qC+++CK+zLgXCZBAIAlYLlygePPNN0vDdPjwYd9B1Y8FuRhhbFV75MgR9dxzzxmChZlH3n777dgyYWoSIAESwNArOyhgGh408K+99pod2SctTz0+C++xaOYJTJo0SRUqVMgQrRdeeMH8zkxJAiRAAmkI2CJcq1evlkYKqyP7yUaPHi1xcXyWuVrFDBd6zBsuZFq2bKm+++47czszFQmQAAlEIGCLcKGs7NmzSyMfoVxPbtYzwkPAaJEJbNu2TXXo0MG4wypdurRasWJF5B34CwmQAAnEQMA24erYsaM0XH4aj6OXLGHHjPBH2KlTp9SgQYNU5syZpe4zZMigJk6cGD4xt5IACZBAnARsE6758+dL4/Xggw/G6Zr7dsNjL3xolxKYMWOGKlGihHGX1bt3b/X7779fmpBbSIAESCBBArYJ18WLF6URwyJ/NP8S+OSTT1SDBg0MwbrnnnvU9u3b/RswIyMBEkg6AduEC5E1atRIGrRVq1YlPVA6YC0BrIX11FNPGYJVuHBhtWjRImsLYW4kQAIkEIaArcKFbtDoTdazZ88wRXOTFwmcP39eYXaUnDlzGqI1atQoL4ZCn0mABDxKwFbhwgBkCNf111/vUTx0O5TAe++9p/72t78ZgvX444+r06dPhybh3yRAAiRgOwFbhQveV6lSRRo6LrNue13aVgDG5TVv3twQrKpVq6pNmzbZVh4zJgESIIFoBGwXrqFDh0qDN3z48Gh+8DcXEsBg4T59+hiChceDuOuikQAJkEAyCdguXBiMiseFlStXTmacLDtGAq+++qrKnz+/IVqDBw+OMQcmJwESIAF7CNguXHAbCwNCvPg+xJ5KtDJXjL+78847DcFq1aqV+vHHH60sgnmRAAmQQEIEHBGuHj16SEM4bdq0hJzlzvYR2LBhg8KqzbjAwAfL0nAYg328mTMJkED8BBwRLj2rOsZ10dxFAD0/n3/+eZUpUyYRrIwZM8qimO7ykt6QAAmQwP8JOCJcKA7z1qFRpLmHwJtvvqmKFy9u3GWhI4YZw4UIHinis3LlSjO7MA0JkAAJWEbAMeFq27atNJAfffSRZc4zo/gIYLmRevXqGYJ17733qr1790bNDAtnDhgwINXAY/1YsWjRoooTD0fFxx9JgAQsJOCYcM2ZM0caykcffdRC95lVLAS2bt2qOnXqZAgWBGfZsmWmspg3b57sh/dgECkIWUpKijxWxGrG6CqP/2kkQAIkYDcBx4QLUwXhCj1v3rx2x8T80xA4efKkQnd2vUYa6gHd3WO1SMI0depUqVuuUxYrUaYnARKIh4BjwgXn7r77bmngNm7cGI+v3CcOAtOnT1fly5cX7hAs3HH9+uuvceQUeRfd+aZ///6RE/EXEiABErCIgKPCNWHCBGlA+/XrZ5H7zCYSASw3cv/99xuChbFZGAxuh/GOyw6qzJMESCASAUeF68CBA9KQYil3mj0Edu7cqZ5++mlDsHLlyiW9/+wpTcn7LrzfKleunF1FMF8SIAESSEXAUeFCyaVKlZJG9eDBg6kc4T+JETh37pwaOXKkypcvnyFaQ4YMSSzTMHvj7qpmzZryQeeOIkWKiFCiswaNBEiABJwg4LhwoUs13rWMGzfOifgCUcbs2bPVHXfcYQhWmzZtpNefHcFDuGrUqCEf1CM+EDL0OqSRgFkC6OiDMYDhPps3bzabDdMFlIDjwoXlMNDY1a5dO6DIrQsby420bt3aECw8rlu3bp11BZjICY0MhAx1yl6FJoAxiRBo0qSJcdzqCyD9jeOJRgLRCDguXHBGr5574cKFaL7xtwgE9u/fL8uNYDYSnOyXXXaZmjFjRoTU9m/GY0KM5cKjQxoJmCEAccJjZvRETfvBXT2NBKIRSIpwdenSRRpcru0UrWou/e3ixYvyiPWGG24wrlb79u17acIkbNF3XUkomkV6kACOF95ZebDiXOJyUoRr6dKl0vC2bNnSJRjc7wbeIdWpU8cQrIYNG6pDhw65xnFcPeOui0YCZgjgWKFwmSHFNOEIJEW44AgecV199dXhfOK2EAJYbuThhx82BKtYsWJJmdg22lyEeNSD+sR0UDQSMEMAxwuGbdBIIB4CSROuBx54QBo7zi4evtqweCOWG7nqqqsM0Ro/fnz4xA5sxdUx3k02bdpUJttF79Du3bvLey00QugYwi7xDlSET4rQFzqhvQojTSnmk5AZhoUEkiZcM2fOlAa5a9euFobjj6wmTpyoypYtawjWk08+mfTAcMeFOyoIFBodfPTjHvYmTHr1eMoBXODoYyjtN6YnY3d4T1VnUpxNmnCdPn1aDt7rr78+KYG7sVAs+dKgQQPjpK5evbratWuXG12lTySQEAFcCOkP7rTwNx4542KIKw0khDYQOydNuEBXD5r99ttvAwE7UpBYbuSJJ54wBOuaa65RCxcujJSc20nAtwT0vJd8X+rbKrYksKQKFx4x4VEBltwIouGRCWK/9tprDdF66aWXgoiCMZOAQQBtAh4Z0kggEoGkCteePXukwa5cuXIk/3y7fdq0aeq2224zBAsrRJ89e9a38TIwEjBLAEMrOGmzWVrBTJdU4QJyHKS4wvrpp58CUQMrVqxQ9913nyFYfBkdiGpnkCYJ6I4bmBKKRgKRCCRduP7+979LIz5p0qRIPvpiO5Yb6datmyFYmTNnVuhZSSOBoBFAr8FwQyewDcMtcCHLSZuDdlTEFm/ShWvt2rVyoGImCD8aHv9huRF9Z4mT8rnnnvNjqIyJBEwRQO/BtGMCMchez2HKjhmmMAY6UdKFC/QzZcqkMmbM6LuKmDVrlqpatapxl9W4cWN17Ngx38XJgEggFgLo/o5ZMzCoHRdy+KAbPB4Pols8jQTSI+AK4Xr00Ufl4PViF/BTp06pn3/+ORXnVatWqVatWhknJSbF/eyzz1Kl4T8kQAIkQALxEXCFcC1atEga+Q4dOsQXRRL2WrNmTapJb+vVq6cQxzPPPKOyZs1qiNZrr72WBO9YJAmQAAn4l4ArhAt48bggb968niD93XffyaMN/ZhDf+ORp/4bS7fQSIAESIAErCfgGuG65557pNH/8ssvrY/S4hz1bOhapEK/MYXV3r17LS6R2ZEACZAACWgCrhGut956S4TLLQsjakDhvhs1amTcWYWKFv7GrPc06whgyACY1q1bVw0aNEidOXPGusyZEwmQgK0EMMwJQxzq16+vRowYYVlZrhEu9LZDw1+6dGnLgrMro169ekUUrn79+tlVbODy7dy58yWcS5UqpY4fPx44FgyYBLxGoE2bNpecv7fffrvCSu6JmmuEC4HopTz27duXaFy27r9x48ZLKkTfeW3bts3WsoOS+RdffBGRMTrA0EiABNxLQHe40+1i6PewYcMSdtxVwjV8+HBprEaNGpVwYHZngEdYWMFZV0jhwoXVe++9Z3exgclfHwuaL7//HO9EDuTg9WMAj/0TNVcJF5Y3QaXUqlUr0bgc2b9Zs2bi76uvvupIeUEqZMyYMcZFQdoTNXv27KpmzZr8kAGPAZceA6EzBaU9f9FHIFFzlXAhmFy5ckmDde7cuURjs33/MmXKiK8nT560vaygFfDNN99EFK4hQ4YEDQfjJQFPEPjxxx9VuHfToeL1xhtvJByL64RLd3x45513Eg7OzgzwHi5LlizSuNpZTpDzHjp06CXihWETNBIgAfcRePnll1W2bNmMcxYruIcKFv5u2bKlJY67Trg+//xzCbZFixaWBGhXJkuXLhU/b7nlFruKYL5KKYzre+GFF1T+/PmFNzrG0EiABNxD4J///Kcs/KlFCpMk484LhvYcK4D07NlTLViwwDKnXSdciAwA0PHBzYb3WvATs1rT7CeAGfbB+x//+If9hbEEEiCBdAl89dVX6v7775fzEucmJhT/97//ne5+ViRwpXDpCWqXL19uRYy25NG1a1epsAkTJtiSPzNNTWD79u3Cm3e4qbnwPxJwmsDp06dV7969DcG69tpr1dSpUx11w5XCNXfuXIHy1FNPOQojlsIwqS6uMtatWxfLbkybAIESJUoI80OHDiWQC3clARKIlwAmDcecsmj78MFjwGSYK4XrwoULAqVYsWLJYJJumRj5Dd9QcTTnCGDgMZhz+IFzzFkSCYDAv/71L4VZL7RgoQ9CMudkdW3LW61aNYG0ZcsW1x05W7duFd/c/h7OdeASdEh33Kldu3aCOXF3EiABMwR27typ2rZtawhWhQoV1LJly8zsamsa1wrX66+/LrAGDhxoK4B4MtePMu+44454duc+CRD461//KsfFH3/8kUAu3JUESCAagV9//VV68+o7rKuuukq56X2+a4UL7zEArVKlStH4JuW3l156SXzD8uM0Zwmgqy2Oi/fff9/ZglkaCQSEwLRp04xXITjXevTooSBkbjLXChcg6fdIhw8fdhMzhZWaUaGYr5DmLIEPPvhA2Ldu3drZglkaCficAB7F16lTR84vtG8NGzZUmMHGjeZq4XrxxRcFIh4busnwiBAVu2PHDje5FQhffvvtN2F/xRVXBCJeBkkCdhM4cOCAeuyxxwzBKlmypJo/f77dxSaUv6uFCwPctPInFKWFO//8888qd+7c4peF2TKrGAjo1bKdGuwYg2tMSgKeIoDXHlmzZjVEC9M2ecFcLVwAePnll6sMGTK4hqVeJ6pAgQKu8SlojmAsCS5o8OydRgIkEDuBOXPmKCzKivMInyeeeEJ5abJw1wvX448/LmAxH5YbbPr06eIPJ3tNXm0cPHhQ6gBLJ9BIgATME9iwYYPCsiJasPBOa/369eYzcElK1wvXxx9/LJDRIcIN1q9fP/EHE7/Skkfg1ltvlXrYtWtX8pxgySTgEQJHjhxR6AWtBatgwYJq1qxZHvH+UjddL1xwGbAxH5YbrHnz5uIPlqamJY/AgAEDpB6wUjKNBEggMoGxY8eqa665xhAtdHrzunlCuO69916Bvnr16qTzLlu2rPjiti76SQfjsAObNm2SeqhcubLDJfujuJSUFLVy5Ur5bN682R9BMYpUBHBxfdtttxmC1b59e/X999+nSuPVfzwhXO+++67A79OnT1I5//DDDwrdsC+77LKk+sHC/yRQqFAhOS7Q05NmjkD//v1V0aJFjcZMPzrCNgw8pXmfwLZt22TBRl23mGMQY7T8ZJ4QrjNnzsiJVrp06aSy1+/b0BuHlnwCeolwdJihRSdw4sSJVIv91ahRQ2EWEnzQyUU3clxfLjpHN/+KXoHPPfecUZc5cuRQU6ZMcbPLcfvmCeFCdOXLl5cK2b17d9zBJrrj+PHjxQesF0ZLPgHMWI0Gt0mTJsl3xsUe4LGgPn/KlSunPv3000u8HT16tNHg4W+atwhMmjRJ6ScQOCcgYH42zwjXmDFj5MTCSrjJsm7duokPo0aNSpYLLDcNgYwZM0qdpNnMf0MI4O4KjRlEC3dekQyPEZEOjw1p3iCwYsUKpesXdYfOY3v27PGG8wl46RnhwlUjKqZWrVoJhJvYrvXr1xcfOGNDYhyt3Fv38ly6dKmV2fomL6xMi/MGj42iiRYCxu9Iiw87bLj7EMAwED1nKuqrTJkysmaWu722zjvPCBdCzpMnj5xUyXoZf/3110v558+ft64GmFNCBGbMmCF1gpH/tEsJ6PdXuJsyY7grQ0PIx4VmaDmf5ty5c2rQoEEqc+bMUk944oBXGEEzTwmXXgE3Gb2f8G4NJzTmKaS5hwBeSKNe3DLOzz1klNw1gQ0+6d1tab/1YyezQqf347f9BN555x1VokQJqU/UKQYUB/Ui2lPCtW7dOqk0LBvttM2bN0/K5uKRTpNPv7zq1atL3Xz99dfpJw5QCj1TAsTIrFG4zJJyLh3Gr+qJpSFYGNeKVdiDbJ4SLlQUKu7qq692vM6GDRsmZXfq1MnxsllgdAKY0RrHBe8SUnOKR4T0o0U+KkzNMhn/7d+/X3Xp0kWObRzf6DSDC2iaUp4TrjZt2khFLlmyxNH669ixo5Tr13ERjsK0uLCdO3dK3eAFNe3/BLRwoYOGWUMDiU+4LvNm82C6xAhcvHhRvfLKK9KhRtfHiBEjEsvUZ3t7TrgWL14sJxauRJy0atWqSblbtmxxsliWZZIAFr/DSf7jjz+a3MP/yXSjZ1aEkE7vY/admP8pOhsh7qgqVKhg1ANWx/jpp5+cdcIDpXlOuMAUJ1exYsUcw/vHH38YPRodK5QFxUQA04HhuMBaXbQ/CWgRMitc+p0YehbSnCWA5UaaNWtmCBbe2+KdPi08AU8Kl34EgolWnTC9EvMNN9zgRHEsIw4Cq1atkpO+bt26ceztz10wdgviZeZRIe6wcubMaTq9P4k5HxWeEOje0qgrzOKO3oO06AQ8KVx6UCWWtnDC3n77bTmhGzRo4ERxLCNOAtmyZZN6inN33+2GqbDQGGI+wvRMz5phZqByennxd3MEXn/9dXXddddJHaGeBg4caG5HpvJe5wzUGZ75oqIrVarkSBX+4x//kPL69u3rSHksJD4CmCAWx4VbVsuOLwrr9tIXeGASbSaM0HTstWYd/0g5ffTRR6pq1aqGYLVt21YdOnQoUnJuD0PAk3dciAOP7XBCOlHhDzzwgJT1wQcfhEHITW4hAMHCMYGGgPYnAT0TBh4Dpn3XhceDekFOcDNzZ0au8RNAx6527doZgoVOGFgTjRY7Ac8K1+DBg+UAcOJlvD75Ma6C5l4CFy5ckGMie/bs7nXSYc9wp6WPX4gTxgLVrFnTmC0e2/DhGDj7KgYXCOCbIUMGYZ0lSxY1efJk+woMQM6eFa4dO3bIQYBR5HbaqVOnVNasWU0NesZEwJjFvmnTptI44Go27VWunb4yb6XwHhIN8Zo1a4jjfwR0w6kHF2uxwjfeg/EYte9QwfR0+ukQePN1gzWsPStcCB+rEeMq5vfff7eGRphcdG+1W2+9Ncyv/9+kX27j4MQVLno+6l5dXJzv/5zs/uuNN94Q4erdu7fdRXk2f9yF6Y4buMiiWU9g+fLlCj1c9UUCeGNGd5o1BDwtXE8++aQcGO+//741NMLkohtCzNgRzSBWGAeDq1tt+Fs3EGa6JOv9+B0/AbzzRGNx4403xp9JAPbEsakvrPiY0LoKx5MgrFSgBat48eLK6Vl+rIvGvTl5Wrj03ZCddzR6UObQoUPjqkU0EDiIIWA0ZwhUrFhRmO/du9eZAj1aip44GscnHxcmVolnz55Vw4cPV1dddZUhWuPGjUssU+4dkYCnhQtR4aSzc0kLPSszbv3jNfiIR4c0Zwi8+OKLclxg8l1adALoSYjjE70OQ58WRN+Lv4YSmDVrlizkCI74dO3aVUHIaPYR8LxwNW7cWA6Wzz77zBZK+sUqOmnEY3rlZnY1jodefPvgHQ4aEC5Bkz4/iBXutvDBsUozTwAroetXATjeateurTiXqXl+iaT0vHDpsTuYq85q+/7776UBLFiwYNxZ604bfBQTN8K4dtQzEvDKNy583CkKgX379qkePXpI2wDBypcvn5o7d26UPfiT1QQ8L1yYABcHT6lSpaxmo5YuXSp540oqHtNX/nxMGA+9xPZ56qmnpO5mzpyZWEbcmwT+RwC9l8eOHWtMuI12B++1aM4T8LxwAdnf/vY3aaS2b99uKUG9QCF6L8ZqeASD9wYYO8N3B7HSSzy9vui4//77E8+MOQSeAO6oKleuLO0MBAsdwo4fPx54LskC4AvhevXVV+WAGjlypKUcH3nkEck31tk5IFTly5eX7sa466IlhwAamMyZMyencJbqCwJYWqR169aGYGF+1LVr1/oiNi8H4QvhwtIAaKQwlY2Vduedd0q+69evN50tRcs0KtsTtmjRQuovkR6htjvJAlxJ4IcfflD9+vUzBAvd3PnY2T1V5QvhAs68efPKQWblaqHIM5YrdoqWew5seKKXo+ncubO7HKM3riaASQdCp8d64YUXXO1vEJ3zjXA9++yzIlyYG8wK27lzp+RnttMHRcsK6tbmgSEMuBMvUKCAtRkzN18S+PDDD1WtWrXkmMFx07x5c3XgwAFfxupZgdwAABxhSURBVOr1oHwjXFu3bpUDDo+HrDC8jMXBa+blvhYtpMcku1iqINyH42SsqJnY8sDjY9TLtm3bYtuRqQND4Ouvv1b6fTaOlZtvvpkzibi89n0jXOCMgw7Poq0wvU7Rc889l252eqwWyo/24Zxw6aK0PMErr7widYLZNGgkEEoAvQJxXFx++eXGefvmm2+GJuHfLiXgK+HCAoIQjsWLFyeMu2XLlpLXO++8k25eGFwMUUrvw0HI6aK0PAFm5MYxgUX7aCSgCbz11luqZMmShmD17NlTXbx4Uf/Mb5cT8JVwrVixQg7ELl26JIwd3dnR4OFdF83bBDBTPOry6NGj3g6E3idM4OOPPzbWbMMxUa9ePZ7jCVN1PgNfCRfw4WDEKq+JGFbSvfLKK1Xu3LkTyYb7uoQAFu/DcTFx4kSXeEQ3nCaAyQn0bCo4FjCNmxVPZpyOg+X9ScB3wqV7BWHgYLymp2qqWrVqvFlwPxcRWL16tQhX/fr1XeQVXXGCwJkzZ9SwYcNkFhsIFj7oQEXzNgHfCdeMGTPk4ETninhN59GxY8d4s+B+LiOA1bLRaNGCQwDvp/V0cKj7xx57TP3yyy/BAeDjSH13Jp87d04aKEzNEq8988wzkgeu1Gj+INChQwep0wULFvgjIEYRkcDnn38uY7D0HRaWt/nqq68ipucP3iPgO+FCFdx0003SSO3fvz+uGmnQoIHsjwGJNH8Q0Kv9cl00f9RnuCiw4nWvXr3k3IVo5ciRQ33wwQfhknKbxwn4UriGDh0qB++ECRPiqh7dC+3w4cNx7c+d3EdAL39zzTXXuM85epQQAXSmGj16tMqfP78hWoMGDUooT+7sbgK+FK7vvvtODuB77703ZvonT56UfSFeNH8RwPGAK/Evv/zSX4EFOBrcUVWrVs0QrFatWnHYQwCOB18KF+oNM2igkTp//nxM1YjluLFfPKIXU0FM7DgBdIdH3aJ7PM3bBLC0SLt27QzBKlOmjPriiy+8HRS9N03At8KFQchopObMmWMaBhJi7S3sh6W5af4igKUqULeYi47mTQKHDh1SmIYtY8aMUpf4nj59ujeDoddxE/CtcG3YsEEObKxUGothtWM0bljagOY/AnpGlHg77viPiHciwkWlfv+Mc7RPnz7ecZ6eWkrAt8IFSji4r7322piAVa9eXfZbtWpVTPsxsTcI4KU9jgu8zKd5g8CiRYvU3XffLfWGusNjfLzHpgWXgK+Fq2nTpnKwY4kRs5YvXz6VLVs29euvv5rdhek8RABLWKDxq1Gjhoe8DqarmMEmdLkRTOWG+UhpJOBr4Zo/f740UhhQbMYOHjwo6StWrGgmOdN4lAC6xEO8eHHizgo8duyYwsw3V199tdQT6mr8+PHudJZeJYWAr4ULRHHQm13FeMmSJZK+TZs2SakMFuoMga5du0o9z5o1y5kCWYppAlOmTFFly5Y1BAvvnDEGj0YCoQR8L1y33XabnATffPNNaNxh/x45cqSkHThwYNjfudEfBLC0BS5oHnjgAX8E5IMoli5dqho3bmwIFt41Y0Z3GgmEI+B74cLsGWikRowYES7+VNvat28vaWfPnp1qO//xHwEcE1atlu0/Os5F9J///Ed17tzZECw8xl24cKFzDrAkTxLwvXCdOnVKToqaNWumW0F6JumtW7emm5YJvE1Ar3DNVamTU48///yzeumll6TXLy4i8MH/NBIwQ8D3wgUI1113nZwYR44cicoEV+CFChWKmoY/+oPAzJkz5ZjA+y6aswTAvkqVKsIfgtW2bVsFIaORgFkCgRCuv//973KSTJs2LSKXHTt2SJo6depETMMf/EPg9OnTUt/FihXzT1AujwTDUpo3b24IVoUKFRS6vNNIIFYCgRCuXbt2yckS7WU8JuvE1R+et9OCQQArXKPOv/3222AEnKQo9+zZI1OogTU+WbJkUVjkkUYC8RIIhHABDk6YaC/j+/fvL2m4rHe8h5L39hs1apTU+ZAhQ7znvAc8xjg5MMbAYS1aePpBI4FECQRGuLCAIE6exYsXh2V2//33y+8Yy0ULBoHdu3dLnVeuXDkYATsYJSa3xuwkWrCaNGmi0nvH7KB7LMrjBAIjXOg9hpMo0qPA4sWLq8yZM3MONI8f0LG6X6RIETkufvrpp1h3ZfowBLC0yIMPPmgIFs4rLBVEIwErCQRGuAANwoXHFmntt99+k99Kly6d9if+73MCzz77rNT95MmTfR6pveFhujSwvOKKKwzR4goL9jIPcu6BEq677rpLTqp169alqvONGzfK9mbNmqXazn/8T2DNmjVS940aNfJ/sDZFiHkEscaZfizIIQY2gWa2BoFACZceu4MJPEMN3eRx0mGBOlrwCGAxQnxosRFYsGCBqlu3riFYGEqyb9++2DJhahKIg0CghAt8IFCYvzDUevXqJdujjfMKTc+//UWgY8eOUv8ffvihvwKzKZpNmzYpzQznE5YC+uijj2wqjdmSwKUEAidcJUuWlEYqJSXFoFGvXj3ZhhfLtOAR0MvfYO0nWmQC6BWIYSO5cuWS8wWihYmpaSTgNIHACdfw4cPlpMPku9ry58+v8uTJozCbAi14BC5evCjHBO4caOEJTJo0SZUrV84QrA4dOqgLFy6ET8ytJGAzgcAJ1+HDh+Xka9CggaBFN2hcOVarVs1m1MzezQT0XfeGDRvc7Kbjvv3rX/9SDRs2NASrUqVKatu2bY77wQJJIJRA4IQLwWfLlk1OxDNnzqjPP/9c/sYze1pwCbz55ptyHHBmhz+PAYgTFnHERR0+mHXmvffeC+4BwshdRSCQwtWtWzc5GTG6X6/XhUeItOAS+PHHH+WYwOq7QTYsA4QpsPD4XIsW3mvRSMBNBAIpXOgVhZPy4YcfVp06dZK/8YKeFmwCt9xyixwLGEwbRJsxY4bCo0AtWJjJne99g3gkuD/mQAoXqgUnJzpk6BnCsRIrLdgEBg8eLMfFuHHjfAti6tSpCu93saQIBgpj5QRMh4bB91qwMJiYPWx9ewj4IrDACpceOHn55ZfLKqy+qE0GkRCBLVu2SOONGVb8aN27dzfESYsUlhjJlCmTsX3KlCl+DJ0x+YxAIIULV536xNXfeLfx/fff+6x6GU6sBLJnzy7Hxu+//x7rrq5OjycK+lgP992zZ09X+0/nSCCUQOCE69y5c0o3TmlPYIxNoQWbQGjHHT+RwCTCaY93/T8emdNIwEsEAidcmNZHn7BpvzEjAC3YBJYvXy7HR5s2bXwFYvbs2RGP+xIlSvgqVgbjfwKBE6558+ZFPIGzZs3q/xpnhOkSwAVNzpw5003npQQnT55UV155ZdhjH8uR0EjASwQCJ1xHjx4Ne/KisUL3XxoJ6NWwMTjdT4bu7mmfMtSvX99PITKWgBAInHChXkeMGHHJCYzn/OhVRiOBd999V44P9MLzmw0cOFBiK1++vFq4cKHfwmM8ASEQSOFC3WIONkzzhK7P/fr1U0EddBqQ4zymMH/++Wdp3G+66aaY9vNC4qeeekpi4+rEXqgt+hiJQGCFKxIQbicBENAzSOzcudNXQO6++24RLsweQyMBrxKgcHm15ui3rQTGjBkjDfywYcNsLcfJzH/77TdVtGhRicvJclkWCVhNgMJlNVHm5wsCe/bskQbeT8vd6JlB0LuQRgJeJkDh8nLt0XdbCVx33XUiXpgx3Q/2wQcfSDzVq1f3QziMIcAEKFwBrnyGHp0A1uZC9/Fp06ZFT+iRX7FcCeLp3bu3RzymmyQQngCFKzwXbiUBmSEdDT3GdfnBHnroIREuLgjph9oMdgwUrmDXP6NPhwCE64orrkgnlTd+vv3220W4UlJSvOEwvSSBCAQoXBHAcDMJgEC7du2ksV+yZImngRw/flxhLk4IMY0EvE6AR7HXa5D+20pgwYIF0thjpWwv2+rVqyWO/PnzezkM+k4CQoDCxQOBBNIhgLuUwoULp5PK3T/rNeiaNm3qbkfpHQmYIEDhMgGJSYJNoFatWnK3snnzZs+CwAzwEGD0LKSRgNcJULi8XoP033YCkyZNkkb/hRdesL0suwrQM95//PHHdhXBfEnAMQIULsdQsyCvEjh8+LAIV8WKFb0agipdurTEgHW5aCTgdQIULq/XIP13hEDx4sWl4f/hhx8cKc/KQvbt26cyZ86sLrvsMiuzZV4kkDQCFK6koWfBXiKgZ52YMGGCl9wWX7GED95vlSpVynO+02ESCEeAwhWOCreRQBoCW7dulca/QYMGaX5x/79jx44V3zt06OB+Z+khCZggQOEyAYlJSAAEsmbNKgLgNRpdunQRv19//XWvuU5/SSAsAQpXWCzcSAKXEnjyySdFAObOnXvpjy7eUrduXfF7w4YNLvaSrpGAeQIULvOsmDLgBFasWCEC8PDDD3uKRJEiRcRvTzlNZ0kgCgEKVxQ4/IkE0hJAJ4c8efKk3eza//W7udy5c7vWRzpGArESoHDFSozpA02gUaNGcveCuf+8YO+//774e+edd3rBXfpIAqYIULhMYWIiEviTwKxZs0QI+vTp4wkkgwcPFn979erlCX/pJAmYIUDhMkOJaUjgfwR++eUXEQKvjIlq3769+Dt79mzWIQn4hgCFyzdVyUCcIlC+fHkRgz179jhVZNzlVKlSRXzdu3dv3HlwRxJwGwEKl9tqhP64noAe0Pvyyy+72tfTp09z8UhX1xCdi5cAhStectwvsARSUlLkLgbLnbjZ1qxZI37eeOONbnaTvpFAzAQoXDEj4w4koBS6l6Nr/JkzZ1yL46233hIfGzdu7Fof6RgJxEOAwhUPNe4TeAK9e/cWUXj77bddy6Jv377iI3oW0kjATwQoXH6qTcbiGIEvv/xSRKFly5aOlRlrQffdd5/4uGzZslh3ZXoScDUBCperq4fOuZkAHhVmy5bNtS6iyz58PHHihGt9pGMkEA8BClc81LgPCSilWrVq5do7mkOHDsnCkdmzZ2ddkYDvCFC4fFelDMgpAosWLRLh6tq1q1NFmi5HLx5ZsWJF0/swIQl4hQCFyys1RT9dSQCP4m644QbX+abHmnltJnvXgaRDriRA4XJltdAprxCoVq2a3HVt2bLFVS537txZ/JowYYKr/KIzJGAFAQqXFRSZR2AJTJ48WQRi0KBBrmJw1113iV/r1693lV90hgSsIEDhsoIi8wgsgSNHjohA3H777a5iULhwYfHLVU7RGRKwiACFyyKQzCa4BIoWLSoiARFzg23fvl38gXjRSMCPBChcfqxVxuQogQEDBohQTJw40dFyIxWmF4/E40IaCfiRAIXLj7XKmBwlsG3bNhGuJk2aOFpupMLwvg29HXv06BEpCbeTgKcJULg8XX103i0EMmXKpDJnzuwKd9q1ayfChdWaaSTgRwIULj/WKmNynMCjjz4qYjF//nzHy05bYOXKlcWX3bt3p/2J/5OALwhQuHxRjQwi2QQ++eQTEYvHHnssqa6cP39e/fWvf1VZsmRJqh8snATsJEDhspMu8w4UAbxXKlCgQFJjxrgt+FG2bNmk+sHCScBOAhQuO+ky70ARqFevnojG2rVrkxa3XjzygQceSJoPLJgE7CZA4bKbMPMPDIHZs2eLcPXr1y9pMffp00d8cNtMHkkDwoJ9SYDC5ctqZVDJIHD27FkRjQoVKiSjeCmzadOm4gNmh6eRgF8JULj8WrOMKykE9OKN+/btS0r5t9xyiwjXTz/9FLV8LC45ZswYBaGrWbOm6t69u5o2bVrUfdL+uHnzZoXB15E+adPzfxKwigCFyyqSzIcElFIjR44U4cCyIk7b0aNHZfHIvHnzRi169OjRKmfOnOJnuXLlVI0aNVSRIkXk//Lly5teMbl///6yDzqDhPtEdYI/kkACBChcCcDjriSQlgDutNCIo6OG06a75FevXj1q0Q899JDCLB8pKSmp0mkhevrpp1Ntj/SPTh/pd24nAbsIULjsIst8A0sgR44cIl7nzp1zlIFePDKRsWS488JdlxmDwEGkaSTgNAEedU4TZ3m+J6AbdKenXHryySdFSMaPHx83Yzw2NCtGSAuRppGA0wQoXE4TZ3m+J7Bu3Tpp/DFnoJNWp04dKRflx2sQIgiSGUM6s2nN5Mc0JGCWAIXLLCmmI4EYCOCuJVeuXDHskXjSQoUKqQwZMsSd0dSpU0X48G3GIFpYiww9EtEzUfdO/PTTT83szjQkEDcBClfc6LgjCUQm0KxZMxGBFStWRE5k4S979+6V8kqUKBFXrugej56GeMeFv80YhAsCre+80EMR/+MDETObj5mymIYEQglQuEJp8G8SsIjAokWLpAHv1auXRTlGz2bBggVSXuPGjaMnDPMrBAYdMvCYEGOzEjHkhV6LEC9800jADgIULjuoMk8SUEoa75IlSzrCYvDgwVLeM888E1N5WrQgNFY+4tPjwmJyholJwCQBCpdJUExGArESqFSpkojJN998E+uuMadv27atlPXuu++a3jdUtMy+1zKbOcaJQQxRBo0ErCZA4bKaKPMjgf8ReP3116XxHj58uO1MtEju2rXLVFlatPB40Mo7LV24fv+l/+c3CVhJgMJlJU3mRQIhBDAFE+460pvJImSXuP68ePGidKzAApJmLFS0zL7TOnXqlJmsJQ3yR0cPdNagkYAdBChcdlBlniTwPwL58+cX8Tp+/LhtTL7++mspo0qVKumWoUULgopJdleuXBn2Ezod1EsvvST5d+7c2cgfgof9Q9PhR9y9oaMH8p83b56Rnn+QgJUEKFxW0mReJJCGANbmQiNu9Tuk0GJmzpwpZbRv3z50c9i/ISzwJ70P5iHU1qpVK0kfKowQrtA8tFhhGx4/2hmv9ovfwSVA4Qpu3TNyBwigYwYa8+bNm9tWWt++faWMIUOGpFsG7pAgSul9Qt97ffjhh6pBgwZqxowZqfJHXphpPjQvCBbu6mgkYCcBCpeddJk3CfyvW/yVV15pGwvdg2/JkiW2lcGMScBNBChcbqoN+uJLAniEh7uuxYsX2xLfzTffLPkfO3bMlvyZKQm4jQCFy201Qn98R0C/Vwrt3GBVkOjtlylTJlWsWDGrsmQ+JOB6AhQu11cRHfQDAdxxYUJaq23VqlVyt1W/fn2rs2Z+JOBaAhQu11YNHfMTgdq1a4vArF+/3tKw9CDnbt26WZovMyMBNxOgcLm5duibbwigRx7uugYMGGBpTHj8iHwnTJhgab7MjATcTIDC5ebaoW++IXDu3DkRGEzNZKXpO7m1a9damS3zIgFXE6Bwubp66JyfCNx0000iXgcOHLAsrIIFCyp0tce0TzQSCAoBCldQappxJp3A0KFDRbhee+01S3w5ePCg5FehQgVL8mMmJOAVAhQur9QU/fQ8gf3794vQNGzY0JJYMOAY77cwJRONBIJEgMIVpNpmrEknkDVrVpUxY0b122+/JezLiBEjRLhC5xVMOFNmQAIeIEDh8kAl0UX/ENC9AOfOnZtwUO3atRPheueddxLOixmQgJcIULi8VFv01fME1q1bJ2LTsWPHhGO57bbbJK+dO3cmnBczIAEvEaBweam26KsvCOC9VL58+RKOBcuHFChQIOF8mAEJeI0AhctrNUZ/PU+gUaNGcqf073//O+5Yvv32W8mjVq1acefBHUnAqwQoXF6tOfrtWQL//Oc/RXSeffbZuGOYM2eO5NGpU6e48+COJOBVAhQur9Yc/fY0ATwuLFu2bNwxPP/88yJcWMiRRgJBI0DhClqNM15XEMCgYYjXjh074vKnadOmsr9da3zF5RR3IgGHCFC4HALNYkgglMDYsWNFeEaNGhW62fTfJUuWVJdddpk6evSo6X2YkAT8QoDC5ZeaZByeInD8+HERrrvuuitmv8+ePSuDmEuVKhXzvtyBBPxAgMLlh1pkDJ4kkCdPHhGvkydPxuS/Hgt23333xbQfE5OAXwhQuPxSk4zDcwSeeeYZEa6ZM2fG5PuUKVNkv0R6JcZUIBOTgMsIULhcViF0JzgE/vOf/4gAtWnTJqagu3fvLvtNnTo1pv2YmAT8QoDC5ZeaZByeJICehZgBIxarU6eOCNcXX3wRy25MSwK+IUDh8k1VMhAvEmjdurWI0LJly0y7j2mecufOrf744w/T+zAhCfiJAIXLT7XJWDxHYOnSpSJcePxnxg4fPizpq1ataiY505CALwlQuHxZrQzKSwTwuLB48eKmXF6+fLkIlxWzy5sqkIlIwIUEKFwurBS6FCwCd955p4jRV199lW7gY8aMkbTDhg1LNy0TkIBfCVC4/FqzjMszBHT39qFDh6br8yOPPCLCNW/evHTTMgEJ+JUAhcuvNcu4PEPg/PnzIkZm3ltVqlRJ0m7fvt0z8dFRErCaAIXLaqLMjwTiIFC0aFERpO+//z7q3tmzZ1c33nhj1DT8kQT8ToDC5fcaZnyeIDBw4EARrsmTJ0f0d/fu3ZLm3nvvjZiGP5BAEAhQuIJQy4zR9QT2798vohRt/kG810IPxJ49e7o+HjpIAnYSoHDZSZd5k0AMBLBMSZYsWSIOLH7xxRdFuN54440YcmVSEvAfAQqX/+qUEXmUwKOPPirCtHDhwrARtGjRQn7/9NNPw/7OjSQQFAIUrqDUNON0PYHVq1eLMD3xxBNhfb355psVOmccOXIk7O/cSAJBIUDhCkpNM05PEMA7rEKFCl3i6++//64yZMigKlaseMlv3EACQSNA4QpajTNeVxOoX7++3HWtXbs2lZ+bN2+W7Q8++GCq7fyHBIJIgMIVxFpnzK4lMHv2bBGo559/PpWPM2bMkO3ooEEjgaAToHAF/Qhg/K4jgMeFt956ayq/9GrJ7733Xqrt/IcEgkiAwhXEWmfMriZQunRpubvau3ev4ad+hIhHhjQSCDoBClfQjwDG7zoCL7/8sgjX+PHjDd8KFiyoChcurC5cuGBs4x8kEFQCFK6g1jzjdi2BY8eOiXDdc8894uOJEyfk/7p167rWZzpGAk4SoHA5SZtlkYBJAjly5BCxOnPmjPr888/l7y5dupjcm8lIwN8EKFz+rl9G51EC3bt3F7GaM2eOmjBhgvw9btw4j0ZDt0nAWgIULmt5MjcSsIQAVkNG78KHHnpIderUSf5eunSpJXkzExLwOgEKl9drkP77lgCEK0+ePAoLTGLy3X379vk2VgZGArEQoHDFQotpScBBArVr15Y7LcwaDwHbsWOHg6WzKBJwLwEKl3vrhp4FmMD06dNFtHDXpT+XX365+uSTTwJMhaGTwJ8EKFw8EkjAhQTy589vCJYWLnxXq1bNhd7SJRJwlgCFy1neLI0E0iWACXZDxSrt3xjnRSOBIBOgcAW59hm7Kwls3LgxqnCdPHnSlX7TKRJwigCFyynSLIcEYiBQvHjxsOJVr169GHJhUhLwJwEKlz/rlVF5nMDChQsVehOGPibEe69NmzZ5PDK6TwKJE6BwJc6QOZCALQRSUlLUkCFDVPv27dXo0aMVHxHagpmZepAAhcuDlUaXSYAESCDIBChcQa59xk4CJEACHiRA4fJgpdFlEiABEggyAQpXkGufsZMACZCABwlQuDxYaXSZBEiABIJMgMIV5Npn7CRAAiTgQQIULg9WGl0mARIggSAToHAFufYZOwmQAAl4kACFy4OVRpdJgARIIMgEKFxBrn3GTgIkQAIeJEDh8mCl0WUSIAESCDKB/wLDE6jHSJSmawAAAABJRU5ErkJggg==[/img][br]What is the scale factor of the dilation that takes [math]P[/math] to [math]Q[/math]?
The circle centered at Q is a scaled copy of the circle centered at R.
[table][tr][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAMwAAADECAYAAADTcc6fAAAgAElEQVR4Ae2dCZgUxdnHvchhYpJPY6JRYxKjuU/P5Eu+gIoHGI03igdqFG+NN0aiGE/USFBOERAQRG4FFuQQFLmXm2WXZbmX5Vh2gWUX2F14v+fXS/XUDHN09/TM9MzU+zzz9ExPd1fVW/XvqnrPw8SQ4YDhgGMOHOb4SnOh4YDhgBjAmEFgOOCCAwYwLphlLjUcMIDJ4BhoPHBAduxtlPKafVJSVScLNtfI5xt2yMzynbJk625ZvWOPbKmtl9r6/RmspSla54ABjM4NH79X72mQ+RU18uGKbfLqrA1yX0GpXDN0qVw+aLFc3HeBXNBrnvyl2xzHn+bd58iF78yXS/svlL8NXiJtRxTJE1NWS/fCTVJQViUl2+ukYf8BH1tgHhWNAwYw0bji4hxD9IuNO6XXwgrp8OkauXlUkVzSb4FjILgBjZNrr3h/sbQfVyIvfrFe3l++VUqr6ly0xlyaiAMGMIk4FOX/eRU18nbhJrnjo2I5v+dcR+BgZrh19Aq5e/xKeWRSmTwzbY28NHO9/HdeufRZtFmGFG2TMaWVMmVttUxYXSUjSypl4LKt0nNBhbwxZ6M8P2OdPDV1tTw4cZXcObZErvtwmVzQe76jslsPWCSPTy6ToSu2ydqde6O0yJxyygEDGAecWrx1t/ReWCF3j1tpLYtivenP7zXPWnYxqF+fs1FGlFTKgi01snNfo4NSvF2ysWaffLZhh/RfukU6fb5O/v5xsVw2cFFcIDELPf3pGhm1crtU7N7nreA8vcsAJkbHl1bXyZtzy639QiyAtHpvoTw6qcyaHdigB4n2NOyXOZt2Sdf55XLbmGJp0SP2TMiMNay4UvY1mj1Qoj40gNE4tGNvg7UMumXUiqhvaDbrD0wolfeWbpHi7dm1N0AggASOme+mkUVR24cgAkHCtPU7NK6YrzoHDGBELCnTQxNXRR1EVw1ZIl3nlVtiXp1x2f69rmG/tV96curqqBI7lnVI95ZX1mZ7U32tf94Chjcuki2WVZFLroveLZRnP1trLWl85XZAH1a//4AML660hAmRvOD3HR8Xy9R11QGtfXqrlXeAqalvlPu6D5VTLr5ZzvrXh2FgYbk1btX29PZAwEpDicqLBClcJHhYqhaU5Td/8gYwlXX18trsjXJG2w5y2OFHyGFHHCmHf/mr8pNr75duM1dK1Z6GgA3dzFdn0Zbdlvg7Ejhthi+3JGyZr2H6a5DzgEHs+sIX66V597ny+6cGyJHHniCHHXaY/Tn88MOlRYsWMnHixPRzP0tKXL9rr6UHwtpAB8/VHyyVD4q2ZUkr/KlmTgPmrfmb7A7+05vT5bhzW1tAOeLII+X888+XE0880QbO1772NXnyySdl8+bN/nA2B5+CXRuCgEizHpZvn67LD8laTgJm8tpqS4Govw3/8ODLclSzL1kA+ctf/iK1tbWycOFCOe+88+Soo46ygfOTn/xERo8eLY2NqVM2ZjuWMBhFR9WyT6H9QoLXSNw219Zne/Pi1j+nALOpZp88NrksrBMxVOw7fYH86le/skBxzDHHSFFRkc0UgNG3b1/50Y9+ZIPmyCOPlOuuu062b8/vDa7NpBhf9jbul86zN4TxG3Odvotzd5bOGcD0XlQhmKbos8p/5my0urp9+/bSrFkzaybp1KlT1O4HHO3atZMvfalpFmKf881vflMGDx5sZpuoHAudXLatVu4aWxLG+7Yjiyw3hdBVufEt6wGD78gNw5eHddY941fKioOa+DFjxsiXv/xla/b4xS9+IVVVVTF77sCBAzJ58mT56U9/as82AOfXv/61lJaWxrzP/NHEAcxrIvVaHaevFfQ8uUJZDRj0BfqMctmARZaVr+qcHTt2yBlnnGEN/q985Ssybdo09Vfc4759+4SZ6Bvf+IYNHGaoO+64Q/jPUGwOYMP27xnrwvoFaRq+QblAWQmYXfsa5eFPwk1ZXp65/pA32aOPPiqIjZklHn74Ydm/37nnIrNNYWGhtG7dJFlToujjjz9ehg0blgt9n9I2FG6ukdvGhNvk9VuyJaVlpuPhWQcYnLXwWlQzC34mk9YcarZRXFxsL8VOOukkWbt2rSd+1tTUyMsvvywnn3yyPdsAwnvuuUc2bNjg6Zn5dBNiaNVXHPHL2dfo/MUVNF5lFWBwptKZj39KNDEmgxzRMbMCg5t9TLI0d+5cadOmjS0U4LlI3saPHy/19bktSk2Wd5gbYZ+n+g6D1nkVu5J9bEbuzwrAIPfHKUsxnGOXueUxGdazZ097Nrj00kt9k3LV1dXJ2WefLd/61rfs5x999NHy4IMPyqpVq2LWx/whgrUAHqp6H2aj+DnwgCmr3iNsGhWjWYKhmIxFq1evtjX4bPT9XDYxm5x++umWxOzOO+8MU3hyfsiQIdLQYGzSYvUN5yP1NniJZhMFGjBsHHUxJeLirXE0ybt375Yrr7zSfvu/8sorvvbFOeecI4MGDbKfWVBQEKbwZJlG+UYEbbMo6pfxZeFLtEcnl0W9LognAwsY/C90myX8UxLRe++9Z7/1v//97ye63NX/b731llx88cWH3LNr1y7p0KGDvbdh3/T1r39d3njjDTPbHMKt0ImVVXVy5ZAl9sqBSDfZIAwIJGAIzqCWYByJmpKI1qxZY5u/8KZnk+4X7dy5U7797W/LzJkzYz5ywYIFlkHnEUccYc9w7HemT58e8550/oHdHHoojrGourrauobr4GeqCWNO3V0a6wDOBZkCBxiin+hgIQSRE7r11lutgQpY0OgvXbrUyW2OrvnHP/5hiZETXYwVQbdu3eSUU06xQcNsw/2bNm1KdHtK/+/Xr59VJwQWACMaKcniqaeeGvOaaPclc47AG0g7VZ9fOXiJMPsElQIFGHznFeM4EjXSCQ0fPtzWyv/pT3+SF154wVoiPf7445ZVspNnxLqGmQPTf6dm/yg8V6xYIUjnlEkOIGb/k2mFJ7ZxLBkBTyQ99NBD1n9cE28WirzPr9+60SyBEOcGVOwcGMDoYCEk0MQ1sW2+9E7as2ePnHnmmVZnH3fcccJGHEI6hinLCSecID169NBvcfX9iiuukNdee83VPVyMAIKBqdulYWpz1113ycaNiZeYrgt0cMOzzz5r8ekHP/hB2NVq9gFMo0aNCvsvnT+QmKkXJmFx8fgMGgUCMPoyjFBGszc5V2o98sgjlnKStzhvyUhiD4FH5R//+Ef55JNPIv+O+5uZC+VkMrRy5Uq58cYbrVmKAcnnl7/8pQwdOlQAezqJpZiqw6effmoVzWyi9ErRZp501o+y0K8p0BCxc03AInVmHDD6Bp+ZxQ1YZs+ebQ9EHMHi7RMYDKzNb7rpJsdKRsAyYsQIX8bMBx98ID//+c/tAYtw4IYbbpB169Krh1B7PY4AiNkGEPE7KKTraq4dulSIFxcUyihgEB2rtwlHp8swxTz2BXQ2G+uxY8eq0zGPOIt17NjRuoflSTzq3LmzsBzzk/DyfOCBB8JE0CwjsUzYuzc9MY+RfqlZ5re//a31nc1+0Ai3ADU22o1eEZjqZQwwKCV1PYvTDb7iXPfu3e2OR+vuxuyeZVLbtm3lhz/8oaC7iaSKigrB5CVVm99Zs2bJ7373O7v+DOA//OEPKSsvsn28CBRofvOb36RNIhZZj0S/9eCK9xcEwx8pI4DB3EXX4DsVHSsGM+DVuhvX4nhLMXVPtOOECROsgXrBBRfI559/bl9y9913W6Jg+0QKviBN+89//mPpd9TgxX36scceS/kAVhIxys3kJt8JW3X7M9KJZJrSDhgi2eu2YU6UkjqTsAxmdqCz2eizeU6WmK2++93vWhKsL774QlgmoaxMBy1atMiKH0AcAdrE3gY90rhx43wzGtXboUvEKC9Iexe9nuo7gRfbDAt51JIiJJOUdsDoVsdOzF0imfP+++9bg4rOZmnh19oflwDe7hhsYgaTTmJv884771jeobwEaBv7MpaazKZ+kS4R02eZWIpMv8pN9jnEltN9oEaVVCb7SM/3pxUwuj8LhpRuCYWg0mswoNItYXJbX7fXL1++3AIJilJAw4f2ImFLVgQNKNQyVonf2b9QRiIBiNt2pOJ6cn4qIQCRaVZVp1ckr9qUNsDgKakajIl+PKtjVTn9yFLs/vvvt5ZhLFvQ5uci0U4sAhD3qtmGSDZEtFm2bJmnJgOWaBIxtTyLZy7jqcAU3UQKQjWGiPOcCUoLYPDB16fUeP4ssZjw8ccf2+YvZ511luDMlcuEKQ6OaV/96lft2QYLbJZuCAzckNK9RLMR4xyzTBCUlk7aROY0BRryeKab0gIYPWBFPE/JWI1HzMtGmI5lueI0+kus52XTeYQQanag/XyQ6rE8dUJqrxLLRiyWuYyTZ2fqGj2zwOiV6Q22mHLA6KGQsEr1QsQ8ZhnG54knnvDyiKy+B7s0nOEQOyvQEN6WwR4vnoBacnFPrBmE5Vo8o8wgMm6Rtp/B5iyd6RJTChiC7Knpk31LtIAViToE8xfVob///e+F2SYeIQliBlKfoEuA4rUl8j+09FdddZUtJQQIbNxj6VKwF+OTSAHL/1yXDh+YyDZ5/T1oWWg/Q3bqdFFKAaNHpIwWCilRIxEZAxIGBm/XWAODDmdTrKRA6i2sjs2bN7cGRKLysuF/ZhvcpIkhoNrHMhXL7Gwa8H7wGkWmeiGzkkkHpQwwxDpWjfGqbHr11VdtS2QkZNHMX9QaXQ0eNrHYRqmPOs8x1rIkHYz2uwzcF6699lrLhIe2IVEjpO2AAQPyxjW68cAB+evBFOvn95wrG3el3h4vJYAhir4KDE74Vi+xdZESqaUYVr4lJSVRx5ySAAGcaG9YZh+lb2AGinZN1AdnwUmMSZltEAooETRStauvvjrndFSxuoNNv3oxkwI+1ZQSwBDdUDVipAetLDMJb081O0QzkFSMYY+SCASARj3rzTffVLfmzBEFLvZveizo0047Tfr37y8E6ch1urcg5OL8iUPHQ6888R0w6FgUWLxo82kIPijqjXnNNdfElQQ5bbiarbJBq+20TZHX4SCHX5B6OSBVbNWqVc6HfSqpqrPHHHaKqSTfAXPN0FDQPZVywk0DKisrhSxgdDrmL37F+MoHwMBnAq4///zzVj4cBRz4+OKLLwr2crlKZERTL2rc3VNFvgJGzynp1gqZBrImv/322+035H//+19f2s2STQ2eWJI2XwoK0EPY8xFHTbWbI0KBzz77LEC19LcqxGxWoEmVrZlvgMGiVFWWNHleaOTIkbbLMT74flAsOyo/nh30Z2BCg2RQuSEDGqyx7733Xs8+REFu84TVVfYYfGBCahzOfAMMqb0VYMaVuTdXKC8vl3PPPdd6I7J5TSYQH5t8FJfPPfecrZtBUpZIOBDkwZBM3bCCJlqNsktjf4j4HRF0NFF9MmVl+l7dDGthCqLO+AKYyrp6ad59rgUYIhl6ofvuu88CC52J0aEX0pcf6ns8TbiXMrL1HpTACFMQ0SuBCrMNS+DFixdna7MOqTcgUS/uR1IgZvYFMK9pmXTHrnI/u0ydOtWeCdApoM32QgokkUf0L1gC5OsMo/OyrKzMcr9WImjAg5v322+/7Znv+vOD8P3+CaU2aIoqa32tUtKAwYUUhx5Qff0w9/4aOEZhfcsgpxP9CmsEl1iaodBUErJcU1x6HQnsbYhnQBgpRM/wHhdpRPhE+sx2ml2+ywZMh6n+xgFIGjBd54fEeSM8KClfeuklu9OYBdz6ejjpXICjQPO3v/3NyS15cQ1Jc7EEV7MNwCGeAZE+3eQDDSKz9DToflozJwWYhv0H7FRsiPTcEjoW5Y6LKy7JkFJFyu+DQWEonANLliwRYlLDG/Vh74cvTrbStPU77FnGS+yIWO1OavTovi64j7qlSy65xOogXHAJbpFKwnxdDQa+GwrnANKyvn37WrGoFZ/oF0TQXveU4SWk/xcBAJUAAPtGPygpwKjYYn8d5F7KQmAH1THYjaVaC43CUpXHEs1QdA5gaXHzzTeHWQow+/NCS8VyOXot/DlLJFUFmJd8cmf2DBhdSdRvibMcLooN69evt3OokKiIFOGpJmXVzF7GUHwOIIJGiYxlgHrJoMNBKODUNTp+Cen798YRTTHNcGD0gzwDRg/jWbXHebBozF90H5ZevXp5bgdiYiezhe6qG/TAdZ6ZkYIbiSjKkkwJTADPj3/8YysWdLZYQZOpWc0yflgyewIMacBVJdyaIGBRi8IM5hNPmCB2XkntS9DdPPzwwzJ69GjbNRlNP+bteFuqtyQb2VxyWfbKN7f3Ieqnr1R0ThJFYaeGsCDoy7StdfX2WPVDkekJMAM1f2o3ZjAsxQiRxABu1qyZECY1GWJ2UWBIdCRKpgGLd25v2bJF/vnPf9oKZvhNeF3iQ7PvCTLdO77JXwZrlN31jUlV1RNgCKLGDHPRu4WOC0eu/8wzz1hmGWiXkf/7QYCAJRfLPOWWrI6ABHGy0fD7wemmZ5AYF/6qFxR9+ec//1nmzZvnXyE+P2lMaaU9ywz2IM3Vq+MaMKWas44b+TZm5ccee6zF6DPOOCPlUjG9kdnwnUHI8jHyg6K1S5cugQM9ddIVnoR9Iu7C9u3uTaPS0T8t+xRaoLltTHIRZlwDRnfUmeswtR4iY/YPvJXYv3z00Ufp4FHWlMEMqN7YsY6Y9QQtiAdL7Ouuu8425qTuWEFnOvlttI5/Zloowkwymn/XgMHXheWYG80+Qeh4AzF943tuKJwDuhQPQYb6qKWmLqUKmtIVqSc6Lj0dIcKBNm3apEVdEM7J2L/0GHmYc3klV4BZrEUcdOoGunTpUlt7jALML5djrw0O4n1KzM4sHI104Qb7siASsyTpQvRlGrGgu3XrlpQk1M+2qpe9FyNhVQ9XgOm9MBRrjPQDiYiN/kUXXWQtNxBFEkjb0KEcUJvoeDoidU1kyvBDn5a5Mw0NDTJlyhQr+CKrCZZo9DvLtjlz5mSuYgdL1tOab3ehO9Qr7gowxEZmOUZqcCdEeCRlPk724mR0Lk7Ky9Zr1L4l3h5FGY9mg6UCMeWQgmLFodp20kknWSlKMqnwLCgLmcp48dtifLkCDIGfAYwTZSXSkhNPPNFiGFMzSi5Dh3JAX27Fs1pQpj3MNNlCKI8J+6QUnoAHhSei6Uy4D5C+nPHLx42EV+e3Y8DMq6ixC+u/dIv+jEO+sxEk1q96u6DcMhSdAwQWVHyKfoVYClekZFwXb9kW6/5Mnie7ACGe9NmGsE9kYUg2q5qXdql431cN8Ra/zDFg3i7cZAOmeHv8ZEZIctRbBRP+eCkZvDQ6l+5xMnOoawBMtiphcY1GYKH2NrQFfRymUuk0r3l5ZihYS8Vu9yb/jgGj0j9j0h+PWKOq6C/4UxQVeQuKEa+MXPpP6aeQlEUS4lrdFi7eHify3iD+ZuWh0hGqWZUxgjtBusxrpmiRWb0kl3UEGDLEER2dtV+igM9PPfWUvcTo0KFDEPstUHVSAwfpl9Lyq3PqiDIwlwIQ4hqNPk6FfaKdtBHL9VSHfapr2G+vlEj/55YcAUZP6Dq4aFvMMiZPnmz5hMOAn/3sZylvfMyKZMkfLF0VKKIdGUTZPqvE6go2/QUFBULARtV2RNAtW7aU+fPnx7rNl/M3jyqyQEPeVbfkCDC6K3IsswKkYio06dFHHy3jx493W5e8u14XFSvtPkd1noGU6xbWW7dulaeffjpMKHDCCSfIG2+8IfyXCiKMsZKWVdY59+WiLo4AozI9kfMlFnXq1Mne6N9yyy2xLjPnNQ6wCQYUkaJiQKLMYXIxPYfGAvvrpEmTLCU3JlTwBPcPrKAx2vVbBD1Kyynj1B5SVdQRYNQURmT+aFRYWGi/IfDIS9WbIVrZ2XyOJReDgxklkpRkDOe4fKGdO3dayW95WShpGuL0F154QfDH8Yt0E68P4mwxopXnCDCX9FtgTWEPTlx1yDOQfGCCTsdjiZyra+5DGp7kCd1COdqGnnPwlE88hWaS1Qjk7YSuZS+jrETgwZlnnmmZ3fhRYYJPqiXZKzM3uHpkQsBU7wlpR6OlsHj33Xfthl1++eVCAAVDiTmgAyLWPkUty6KJnBOXkP1XDB48WL7zne/YLw6Aw3J/27bYgienrVYRj/DGdEMJATNf0/BHRrbEZohIiTTEmL+4YbvYG3uWZbFILcuCbHAZq+5+nVeBONDXMM744Brdp0+fpIrAkYxZ5kqXqVkSAubDFdvs6WvhlvAMVhhU0gA2aj179kyqAfl2s7I+jmeur89C0ZZt+cIzNv0ErD/77LNt0LDHYSvgdbnacfpaa1zj5++GEgLm1VkbbMDs3BcKIIBJg1pjIk6uqqpyU27eX6uWW4mkYOo6Zpt8J2YbBCTK1Z2X9fe+9z0hPnesZW0snr2rhV+KpSqJdm9CwNxX0JQ6QA+EVlFRYUV+p8LERg6Cr0O0xgX1HBt+Zhg+id6QDBB1bVDbk856Mdug2MQKWomgOeJ3hS+OU5q6LpS8eNLaaqe3JdbDqCSvt45uCh5AhTt27GhPjaDbkOFAujnAjMLYY+/Mi5sPAgJCQTlZ7azduddeOfVb4lxknXCGIW4ymyOVQpxUesoN9fTTTxdk54YMBzLFAWboFi1a2NsDgHPOOedYex48QGMR0VqVaJlkxk4pIWDwruTBRA3EolRZz7LpcjMFOq2Quc5wwC0HcA9A6HTKKafYs43KPBBrttnXeMAGDPt0p5QQMBf0mmc9mDA1r7/+uo1kciMaMhwIEgfQz7Rt29YGjVqmDRkyJKp5jbLAd+N9GRcwjQdCKHygf4GcfPLJVmVAMht/Q/5ygDclSYyyLUK+v1xI7mnwEMNfIhSpvQ3OjK1atZJVq8ItVYjcyurp8clljguNCxgVdPz/us6S089sMsNmqktWaeS4dnlyIbZ3RI1UHayOvXv3zhMO+N9MfG4ITazE8vAUJXvnzp2lrq7JY/iyAYsswCAJdkpxAVNes8964Gk3dpCjmjVpWq+//nqnzzbXOeAAYEGXoEASeWzfvr2Dp5hLYnEAhSdu8splHhE0YnqsoAlGyQxz+0fO8xPFBUxJVZ2c++8xctTxTUux0047LeXOPbEanqvno80skaDJ5lyTme43lmgIq7p27SqEelK8RdL7q+vvl/NeHCsExnBKcQFTuLlGTrigrRx2MCgbBZJhF98FDOPMJzkekAZPdWC844UXXmh47WG8ET9g4sSJMmPGDOnRo0dYRjXF7+PObS2te093ipf4isvPNuyQY89pZQNGFYJImSnOfJLjgTItUnyNdzS89s5r5VsTjb9Hfft78r+dBvsDmFnlu+S8l8bJkd88Xo5q1szaQLGJMh9/eHDMMcc4mmEAi+G5PzzX+cjK6X/OvFBa93NugBl3Sbb0YPDxs/41TDqPnGzZPaFZNR//eBDtrRd5Dn8Yw3P/eK54efmbo+SPnT+RWJ7E0aaduIDBilOZDwxc5tzeJlpB5lx0DiA6jgSI/hsvVkSkhvznAFH8Gd83jXQeOy8uYLbUhhJq9lxgFJX+d1nTExEd6yBR3wHLoEGDUlVs3j9Xpb+4c2yJY17EBUytFvQsmnuy41LMhQk5gOiY4HZoqHGUIgmVMWxNyLakLsBlhRkmWqyKWA+OCxhuat69Kdr58zPWxXqGOW84kJUcUNkonpq62nH9EwLGy0Mdl24uNBzIIAe8TAYJAdPKw7SVQR6Yog0HHHGgtj4UY9nNdiMhYLxsjBzV2FxkOJBBDngVaCUETNsRTYGbr/twWQabZ4o2HPCXA0u37bZVJoOXO4/hnBAwT0xZbT34gt6pjajuLzvM0wwH4nNgTGmlDRgsWpxSQsB01zKPbaxxn7HJaUXy8Toi9aucMImO+cifVLa5y7xyGzBba+sdF5UQMAWrQ5lnMcY05B8H9LQWSlkZ6+hfqeZJcOAfk8oswOB16YYSAgafGGUekygZrJuCzbWhcLGk7dPzw0T7bvjlLweUWcyNI5z7wlCDhIDR/fo7fW6Ul352G0aVzCjR0l34WY551qEcUPrFx6c4V1rylISA4aIr3m+KTXbHx85dOQ+tojkTyQFcZQ1gIrmS+t+bDrres3IiO7gbcgSY9uNKrGXZZQMXuXm2uTYBBxRgEsVXTvAY87dLDszYuNPeZowv2+7qbkeAefGLUG7zPQ37XRVgLo7NAQUY9iyG0seBAcu22IBZsb0pgozT0h0B5v3lW+0C5mxyLrN2Wol8vU5JxAxg0jsCSDeuBFn1+w+4KtwRYEo1SVnX+eWuCjAXx+aAAgx5TiL1MO3atZP+/fvHvtn845kDpBsHMORudUuOAMNDWx8MenbbGLPxd8vkWNcrwMQ7kn0Ml1pD/nBAj9rvxuhSle4YMITTBJUtesyVBpfTmCrMHMM5ABAQKZNdTNe98Ful6wNMZBI2oAnnnddfZE1Wy7HPN7jPPOEYMEO11H1eCvLawHy+D5AQ5QTQ5FP68VT2+WPaix8do1tyDJh1WgIaL1OZ24qZ65s4gMhZLdnIXGYoOQ6orYWb8LB6iY4Bw01KgekmyoZemPnungMs1RRgjDTNPf/0O1Zqwis3SZT0Z7gCjC6OqzP6GJ2PKf1uAOMPe3X9y1yP6hFXgBm1cru9YZriIpGmP83Nz6ewDDOA8afvH5q4yhq/Fybh2+UKMBW7m9JfIGV40kWkDX+am59P0fcw+ckBf1qNhYrKOHb3uJWeH+oKMJRC0DMAQyo/t1pSz7XMwRud5JVHSoZImRkGMbMh7xzQpbyslLySa8AMKw65dg4vrvRabt7fh/4FUXGXLl1k2rRpogMIoDz33HM2WPCX0f/Pe+Z5YMAdHxXby7Fk1IiuAUP2WZUo1k2ITQ9tzOlbnHpbYqBpxMnJDQVdJYLgKhlyDRgKU4ExWJqR1s+QNw7069dPrrjiCjn11FPtjT3LL36zBEPjbyh5DnTT4lLM8KDd12MA5bMAAAkuSURBVGvgCTDT1u+wpWW9Fpog5TpDzffgcYB0FrzcMbpMljwBhkJxJqMSJl5Zsl1g7k8lB0g7yTjl44eFimfAvDprg12RRVt2p7LN5tmGA545QBwKBZhil85i0Qr1DJjl22rtijwzLbmNVLSKmXOGA8lyAN1Lyz7zrXHqlzmXZ8DQGIJiKPSu37U32faZ+w0HfOWAvtn/cMU2X56dFGCmrqu2AWPyx/jSH+YhPnEAy/1L+i2wxicB9f2ipABDJW4ZtcKqFLk2iIhuyHAgCBzos3iz/TIfuMx5sPFEdU8aMAVlIYNMBAGGDAeCwAElxb1sgL+hwZIGDMxpM3y5hWYsAHbsbQwCv0wd8pgDg5aFohy9s2izr5zwBTC62f+bc01UGV97yDzMNQdUEjD2MMnYjUUr2BfA8OCrP2jSprbsUyh7G02wv2jMNudSzwGkYUpy6zYMrJPa+QYYPRpH59lmL+OE+eYa/zmg3OgJNp4Kr2DfAEPTMZNR6F62rdZ/bpgnGg7E4cDrczba4y8VswtF+wqYqetCRpl3jS2J0zTzl+GAvxwoqgxZnmBsmSryFTBUEtdlNcvgbGbIcCAdHMDtWI27VMab8B0wm2vrhQSyVL7VewvFRPtPx3DJ7zKGl4S8gN0mSHLLOd8BQwX6alrWF2asd1snc73hgGMO4AHcesBC6wWNHpBALamklACGCrcdWWRPkfgkGDIcSAUH9NxFfispo9U3ZYCZWR7K8nTbmBXRyjbnDAeS4gC5itS+5Ybh7pK7ei04ZYChQh2nr7UbZOzMvHaRuS8aB9gbXzl4iT2+SMOXDkopYIhbpiwAeBOMW+U9HlQ6mGHKyB4OPHowCj/j6vXZG9NW8ZQChlbMrwj5VF/0bqEYR7O09W3OFqQLlf7+cXr1fSkHDL3Wb0koCScB1QwZDnjlwLyK0L7l4r6FsjHNnr5pAQzMQT6uNmjG1szrcMnv+/Y17perhoT2LW5ThvvBvbQBJgiN9YNh5hmZ40AQXrppAwxsnqtNp+xnSHBjyHDACQfQsagVSiaX9WkFDIzRN2xXDlli4gA4GS15fo3u45JpwVHaAUPf68HViBeFeYMhw4FoHJiwusqeWZhhiFSUScoIYGiwLkdPJsFNJplnyk4tB2aX77LS3Kul2Ogk8rr4VdOMAYYGtB/XlJwJhpAO2pDhgOLAiu21cnHfprhijI/+S7eovzJ6zChgkJzpRpos1QwZDmBxrFyNAUvX+cEJrJJRwDA0CP6n2wR1MVFn8hox+OFjSKmWYUFzD8k4YBgdJVV1dlhPGGUUm/mJGWYWHSwk7goaBQIwMIW86UT6UG8WLJ0N5Q8H2LPoy7B7x3vPdJxKrgUGMDSSPDOtBzQlagI45FU3lPscmL1pV9gGP4gzi+qFQAGGSq3ZuVeuPZhiDdCg1a2pN+FnVYfl2hE9S4sec+2VRdD2LJH8DhxgqGD13gZpN7opKwCguX7Yctm4K7W+2pGMMb9TzwFdg08/B0kaFqv1gQSMquz9BaX2m4eEnku2mtSAijfZftRtwwDLewHRsyTia6ABQ+U7fLrGBg2MfX+5f7k+EjHH/O8/B9C96VbH9GkQNPhOWxp4wNCQl2auDwPN0yanptP+DdR1WKvr/iwYUhItNZsoKwADQ0mpoQIE8lYijvNis0TLmrGmW6nTfwhzstFdPWsAw8goq95jpwiE6XxInmMouBwguotuaEufZbNiOqsAo4aFHryNDmCf00gWUEOB4gBxw3SzJ3zwM+FW7CdTshIwMICNom4Z8NeBi7Jq8+hnJwbtWfg3Rb7UiO6ysSb7VQNZCxgGyeode+RWTV/DbHNvwUrLNi1ogyhf6jOipDLMWoM+SWfcsFTzOasBo5jTa2GFnN8zpC2mk96cm77gbqoe+XwkP4uecoI+uHHEcvkiTREp08X7nAAMzNqwa688OqksTPxMzICCsqp08TJvy9EzfwEUouj38Tl7cVCYmzOAUQyduKYqLDwtHfjwJ6tk4RZjJaB45NcR0xbdwhheYziZ6pQTftXfy3NyDjCKCV3nlYfNNnTmAxNKBctYQ8lxYOCyraJSe8NXPhjMpjLzV3I19u/unAUMLFpVvccCiepUdST/5vT12aVh9q/LvT0JqT3LrMsGhtwv4CeSylQlYPVW09TeldOAUaxjORa5v6Gz241ZISzhDMXmAIrHboWbwjxi4d0l/RZYQKlt2B/75hz8Jy8Ao/oNr75IY046H2kOphtb6+rVpXl/JGscQUla9gl5wcIrHPywNN6fp4rivAKMQgH6m2c/CyV7YiCoD66xY0rzM/vzup17rdmEtN2KH+rInmXAsmCEOlL9mIljXgJGMRppDpbQl/ZvSiqqBgfHln0K5Zlpa4TUg7lMLLmGrthmGUPq7VffiUyKNMxQEwfyGjD6IJi0ploemVQmzbuHK0AZOLxdWZ4UrK6SHXsb9Nuy8jtB4Acs3WLFTIhU+NJenPXQrRRvN8HiIzvYACaCI7vrG2Xw8q1y25jiQ5Yl6q1LKKCXZ6634vwSRyvotHbnXvmgaJsVXVQPMqLaw/HC3vPl6U/XyOcbcntGTbavDGDicJC9Dn7m13+4LCZ4GGw3jyqSN+ZstHx28NHJZNCOTTX7hASp7DcAALOFDgz9OyDBnAVfo/3G2DvOSAj9ZQAT4kXcb9v3NMjYVdstYcFVQw7dFOsDke+t3lsopFsnvtq7izdbsxFv+qo9DUllK6it329FC126bbclnOgyr9xaSl4/bFmY9XZkffhNdJbbPyqWt+ZvsuLAxW2w+TMqBwxgorIl8UkEBiNLKhO+xaMNXM6xd8BF97IBiyxTnrYjiqyNN9YI94xfaUXNAQTsnxBKoCBs3j0kzYv13MjzavZj1slXUXDi3nR+hQGMc17FvZIZCJ91JE6vzNwgiKdxnoomRIgc1Mn+Bnjokggugdad9O5YD5u8O3G7zNOfBjCe2ObuJlyrkcKRTZrl0KuzNsi/PltrbcLvKyi1lkkIEggQwab8r4MWC7oQRLp3ji2xpFkdpq6W52ess/ZKPRdUyOCibZZdnFG2uuuLZK82gEmWg+b+vOKAAUxedbdpbLIcMIBJloPm/rzigAFMXnW3aWyyHDCASZaD5v684sD/A0Me7E3llBZ+AAAAAElFTkSuQmCC[/img][/td][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAZAAAAGBCAYAAABINefyAAAgAElEQVR4Ae2dB3gUx9nHP7f02EnciGMHbMdxAJe4l4Dt2CbuxsTdwRRTjemm996NwTSD6WCD6UhIQiAEQkIIoYIKoAaogABVBBLqer/n3WTHe6p7d7u35f7zPHpOdzs7885vZue/uzPzzv8RAgiAAAiAAAi4QOD/XDgHp4AACIAACIAAQUDQCEAABEAABFwiAAFxCRtOshOB8qoyulSWT1cqiqiqptJORUNZQEBXAhAQXfEicT0JFJblUUZREiUVxFBszkEKzw6g4Mwt5Hd6DW1NWUzrT8yi5fHjaWHMEJoT2ZumhHekMQc70NDgdtRvz9PU078VdfK5kzruvNXhr+uue6j37odpYFBbGn7gdRof9j5Nj+hKX0f1oyXHRtCqxMm0MWku7UhbRoHp31PI2R0UeWEvJeQdptTCeDp75RSxKCGAgN0JQEDsXsMWL19ldSVlFCXT4ezdtC1lCS2KHUpjQztQz4DWDp1+bREww/f+e5+laYe70MqESRRwZh3F5YZR7tVzFq8RmA8CPxGAgPzEAv8ZSCC/9IJ0B8939KsTp9CMiM9oYNBzbotEF9/m1CvgIeLOfNj+V2hc6Hs09XBnmnv0C1ocO0zq3H84OYe2p35Lm5MX0rrjM+i7+HG0IGYwzY7sSZPDP6HRB9vTl8EvUd89T1J3/5bUyaeZW3Z187uPRoa8SfOjB9CmpPkUetaXThUmUmlliYE1gKxBwHkCEBDnmeEMNwjwa6dD5/ykzvqb6EE0KuRt6u5/v+oOuZvfX2lUyFvE525OXkDBmVulpxN+hcWvsvhpJafkLF0uL6TK6go3LG381LKqq1RYlkPZxel0+tJxOp4fSdEXgyns3C7am76R1iROo5kR3WjQvudVl42fmvrteUp61cav3vxOr5bSbdwSHAUB4whAQIxj7xU5F1dclsYH+KlixIE3VHemA4LaSuMOPN4QmL6e4nMPU97V85ZkVlVTRZmXUyjifKD0pMNPPvwkxE9Gal618ZgMj8HsSF1KKYXHLMkARtuTAATEnvVqWKl48DgmJ0QawOYB68Y6SB7EHnPwHWmQmwe9eRCcB8UrqssNs9/TGfPsr5P5URSUsZnWn5gpvTbj12WNvSbr4d+KZkf2ol2nV9GZSyc8bTLyAwFBAAIiUOAfVwjU1NRQQl4E/Zg0nyaEfdioYIw88IY0vhF5IYgKSnNdyc6rzuHZXHvSf5DGSvoEPtYg2z67H6V5Uf2lGWFZl9O8ihEKaywBCIix/C2Ze1JBtDRNdurhT6mL710NdmxDgttJ02gPZftL6ywsWVgTGZ1edFIaF+EpyY3NQuu/9xlaFDNEmtJ8oSTTRCWAKXYjAAGxW43qVJ4j5/dId7k8iN3QaymeNcXrJEKydlDe1WydLEGyMgFec7Iz7TuaEdGNPvO7t8F6GbzvBfr+xGxiAUIAAS0JQEC0pGmztJIKYmlVwiT6fPcj9XZOffc8JU13DcrYJM1GslnxLVccHkvZkrJImsVV3wJJFv6xBzvQrtOriWfDIYCAuwQgIO4StNn5/MqDF+wN2/9qvaLB6yd2n1knzSqyWdFtVRye+RWXGy6tmOc1J/U9NfJAPE87RgABVwlAQFwlZ6PzyqtKaV/mZuIxjfo6mvFhH0grqXltBYI1CfDrrrXHp9EXgU/WqeMe/i1pWdxYSsw7Ys3CwWrDCEBADENvfMbRF/fTwpgvqXM9A+GD9z1PG5PmUdblVOMNhQWaEoi6ECwtxOzkc0cdMRm870VpdXzWFczm0hS6TRODgNi0YhsqVlphAq07Pp14/KL200Z3v/tpadwoyaVIQ+fjd/sQYNcpPH7FTiZrtwX+ztOy2bVMcUWRfQqNkmhKAAKiKU7zJsbjFuw2pL6OYtaRHpI/phqqMW8BYJmuBM4XZ9DWlEU0bP+/6m0j86L64RWXrjVgzcQhINasN1VW80CqT9pyyb9SbeEYffAd8j21kgpKL6pKC5G8hwCv81mRMFFyaV+73bB3YfY0gAACTAACYsN2wK8meDpnbV9LXwQ+LrnLOA33FzasdX2KxP67vj7at85TycRDHxGvDULwbgIQEBvVf1F5Pr3V7Z/U7MFfUdthvxMXPW+MxJssIYCAqwTYRcqyuDGiTclPJuzLjN3RI3gnAQiIDeqdNyli9+FPf/EH+r//+z/x17LdH2lD5BIblBBFMAuBiyVZ0o6Mn+683UFMeN3QvswtZjETdniIAATEQ6D1yObcldOSrym+G3x39S10w6+uk8TjmmuvESLyy1/+khYvXqxH9kjTiwmwM0zeMphdzctPI/zJblN2n1nvxWS8q+gQEAvWN/s0Whw73OHCvfvFXwnRWLFiBXXo0EF856eSZ599luLi4ixYWphsZgI8xXdz8jfU0/8Bh/bIe877nlpB1TVVZjYftrlJAALiJkBPnp5ceIzmRw90uFD5ru/jac8LsXj99deFSatWraLbbrtNHGMhGTNmjDiOf0BAKwIV1WXShld9Ah93aJ+9dz8seW7Gdr1akTZXOhAQc9VHvdZcKM6geVEDHC5MFo5ZR7pTdHYI3XvvvUIkkpKSHNLIy8uj7t27i+MsIs2bN6fg4GCHePgCAloR4K14eUdJ5ast9uLsk/adVlkgHZMQgICYpCIaMmN76rd1dqfjaZUnC6KkUwYNGiTEYebMmQ0lQz4+PtSyZUsRl4XknXfeofJy79n9r0E4OKALAd4bfmhwOwchGX2wPR3LDdUlPyTqeQIQEM8zV5Vj9MUDdfYQn3u0L7ErEjns379fCEKrVq3knxv9HD58uDiHReQ3v/kNzZs3r9FzcBAE3CFwIGs7DdjbxkFIvj02EpuMuQPVJOdCQExSEbIZ+aUXaHHsUIeLjWe28K5+tcOTTz4pxCAsLKz24Qa/Hzp0iNq0aSPOZSF54IEHKCMjo8FzcAAE3CHAXhF41pbytVZ3/5YUcGatO8niXIMJQEAMrgBl9rtOraLPdjnuLLfh5FfKKOL/KVOmCAHo1q2b+N2Zf2bNmkXXXPPTlN9rr72WPv30U2eSQFwQcIrAqcJEYncoSiFhp40n8o86lQ4im4MABMQE9ZCQF0HjQt91uKhmHune4Bak8fHxQjxuvvlmt0rAg+7t27cX6fHTCI+VJCT89KrMrQxwMgjUQ4AXHfYJfMyhzbP/rauVxfXExk9mJQABMbBmrpRfou/ixjpcRDx/nt8ZNxZee+010eFv3bq1saiqj/HakT/8wXEl+9SpU1Wfj4gg4CwBntq7KmGyQ/vn7ZPZxTyCNQhAQAyqpz3pP1CvgAcdLh7eMY7n0zcWlixZIsSDxzG0DF26dJHGQvgpRP576qmn6MCBA1pmg7RAwIEAe/+deOhjh2th6uHOlFYY7xAPX8xHAALi4TpJKoilyYc+cbhYeEOflMJjTVpy7tw5uvHGG6XO/YYbbiBe46FVCA8Pp1tuuYWKiopox44ddP/99wsRYTEZPHgwVVZWapUd0gGBOgTYBUrtFe3rjs+gymq0uzqwTPIDBMSDFbE6cYqDcPAq3b0ZG1Rb0LFjR9GpDxs2TPV5aiL+61//ooULF4qoNTU1NHToUJEfi8hf/vIX0uqVmcgI/4CAgkBReUEdr7/99z5D4dkBilj41ywEICAeqAneV3x82AcO4rE8fjwVV1xWnfumTZtEZ/7nP/9Z9XlqIq5bt454SnB9ITQ0VPKjJb/S4s/OnTvThQsX6ouO30BAEwLxueE05mAHh2uGpwEjmIsABETn+uABcaXHUl6Jezw/0qlcy8rK6O677xYCwgsItQz8ZOHvX3ediTKPGTNmiPxZRH7/+9/TsmXLlFHwPwhoToAdMiqn/PLrXnbtg2AOAhAQHethZcIkh8a/PH6cS7kNGDBAdN4///nPac6cOS6lU99JEydOpI8++qi+Q3V+O3HiBL311lvCFhaSN998k44fP14nLn4AAa0IJBfG0vADr4prqYd/Kzp0zk+r5JGOGwQgIG7Aa+jUjKIUGhf6nmjwnXzupH2ZmxuK3ujv+/btEx1227Zt6ejRo1Kn/dBDD7k9HnH69GnixYO1HTA2ahARfffdd3Wm/E6fPr2p03AcBFwmUFVTWWcLAx5gRzCWAAREY/77s7ZSF9/mQjz4PS7v3+FqePzxx4WA8EwpOfCYSOvWrSWHiMeONT2DSz5P+cljGaNGjVL+pPr/ixcvEk/7VY6NPPPMM3Tw4EHVaSAiCDhLgGdqKV9p8YzG88XpziaD+BoRgIBoBJKTWZEwwaFxL4+f4FbqkyZNEh30iBEj6k2LxyZ410GeZnv5svpB+aCgILrrrruooqKi3nTV/rht2za67777hJ0sKEOGDKHq6mq1SSAeCDhFIKUwzsHRaHf/+yns3C6n0kBkbQhAQDTgmF6URGMVrki6+N5FwZnurRDnpwr57r4pT7vZ2dnUs2dPuvXWWx2m4jZWNH4dtnz58saiqD5WVVVFX375pbCX7WZR2b698RX1qjNARBCoRaC6ppq+PTbC4YZt7XG8Rq2FSfevEBA3EbNPn86+d4mGzD6tMoqS3UyV6JVXXhEdsq+vr6r02CNvu3btiFePNzarimdPPf/886rSdCZSSEgIPf3008JuFhJ+zZWTk+NMMogLAqoJBKZ/L649frXFK9rPXTmj+nxEdI8ABMQNfryWQ/k+lp3BaREWLVokOuEePXo4neTatWulXQo//vhjSk52FLPS0lK64447dN2RcNq0acJ+FhH2scUD7wggoAeB1MJ4GhnyprgWeffD0LPqbrr0sMeb0oSAuFDbZy6doDEH3xENtotvC9qftc2FlOqekpWVJW3yxB3v7bffTgUFBXUjqfxlwoQJkrv20aNHCzckvKFU165dVabgerTExER64403HISEpwCfPOn6hALXrcGZdidQQzW09NhocU3yjd2axGl2L7bh5YOAOFkFR87voU4+d4iGOi70fcq8nOJkKg1H/+STT0Snu3r16oYjqjzCU3V5thUPmLPH3euuu47S0z03a2Xp0qXSokMWRPmPB/4RQEAPAryNrvKtwNTDn8JFvB6g/5cmBMQJuDzeoWyc7Ipay7Bx40bRyf773//WMmniWVc8cD55srY2qzHy/Pnz1KlTJ1E2FpJnn32W2E0KAghoTYA3rRoV8pa4VkeFvE05JWe1zgbpEREERGUz8D21XDRIFpHA9PUqz1QX7erVq9S8eXOpk73++uspNTVV3YkWirVlyxbJIaP8JMKf7LCRHTcigIDWBOYe/UJcswOD2hK/ekbQlgAERAVP3lZW+eShx5zzfv36iTv0r76qfxtbFaaaPgqvOxk0aJAoK4sIu45nF/IIIKA1gW+PjRTXbs+A1sS7fyJoRwAC0gRL5Uwrnt0Rm6P9Suu9e/eKDlWP6bVNFNGQw+wQkqcbK59GPvvsM8rNzTXEHmRqXwLrT8wUIvLpztvpcPZu+xbWwyWDgDQCfH70ANHweKvZ1IK4RmK7fujRRx8VHWlEhHfdIfG2uUoR4U2teLAfAQS0JLA99VtxLfPbBGybqw1dCEg9HHmv5mmHu4gGN/zA65Stk78dnmord6Cu+qWqpwiW+ik+Pp5ef/11wYF5tG/f3mknj5YqNIz1OAHeRlr5KnpnGrYjcLcSICC1COZdzSbes0NuaJMOfUyXywtrxdLma0xMjOg0H3jgAW0StXAq3377Ld10002CyTXXXEOzZmETIQtXqelMP5TtL65tvsa/PzHbdDZaySAIiKK22GvuoH3PiwY2J7K3rjOEeBtZ+enDzw/7G3BV8L7vn376qeDCfNq0aUOHDh1S1BT+BQHXCcTlhlF3/5biOv8ubqzriXn5mRCQ/zWAxLwj1CvgIdGolhyr3/utVu1lwYIFopPs1auXVsnaJp3NmzfTPffcIxixkPAqegQQ0IJAWmEC9d/7rLje50X10yJZr0sDAkJE/11d3kw0pnU6e/XMyMigX/3qV1Ln+Mc//pEuXbrkdQ1PTYHLy8tp4MCBDiLSsmVL8vHxUXM64oBAowQulGTSyANviOt+Sngnulp5pdFzcNCRgNcLCO8UKI938OfWlMWOhHT4xk4O5VdX7PgQoXECwcHB9MQTTwhmzK579+6Un5/f+Ik4CgJNECiuKKLJ4f8RfQBWrTcBrNZhrxaQ2q5J2DW03mHDhg2iI3zvvff0zs5W6bMbFll4+fO2226jVatW2aqMKIwxBJSr1ocEv0wFpReNMcRiuXqtgPBrK+WThx6ry2u3heLiYvrzn/8sdYI33HADnTp1qnYUfG+CQFxcHL366qsOQtKhQwdKSdHOoWUTJuCwTQksVaxaHxf6HlVUl9u0pNoVyysFhAfMO/n8NObhCfHgKuvbt6/o+L7++mvtatELU1q8eDH99re/FTzZy/CcOXO8kASKrCWBRTFDxI3lzIhuWiZty7S8TkB4+1nlbCtPvLbilrNnzx7R2b3wwgu2bEyeLtTZs2fpP//5j+DKr7Wee+45Onz4sKdNQX42IjDrSHchIgtjvrRRybQvilcJCC8SHKxY5+GJAXO5yh555BHR0UVGRso/41MDAj/++CO1aNFC8GUhGTlypAYpIwlvJFBZXUHjw94XIrIyYZI3YlBVZq8REHZPMlqxi+BanafqKumPHz9edG68OyCC9gR4q97+/fsLziwirVu3pl27dmmfGVK0PYHCsjwaGtxOiMimpPm2L7MrBfQaAVH6tlpyzHML0qKjo0Wn9uCDD7pSRzjHCQK8cdZjjz0mmLOQ9OzZkwoL9XFH44RpiGoxAlmX06hP4GNCRPxOu79DqMUQNGmuVwiI0qsuuyfxZHj55ZdFZ+bv7+/JrL06r4kTJwruLCLNmjWjNWvWeDUTFN55AkkFMdR1VwshIgeytjufiI3PsL2AKPfzmHjoY119W9VuJ998843oxHr39qxw1bbFG7/HxsaS0t8YC8m7775LaWlp3ogDZXaRQPTFYCEgPPU/6mKwiynZ7zRbC4hyJ0F2ya6XV936mkV6ejr98pe/lATkjjvuoKKiovqi4TcPEFi4cCH9+te/FmLOa3Dmzp3rgZyRhV0IhGTtECLSxbc5JRVE26VobpXDtgLie2qFqHDeDEqv/Twaov/hhx+KDmvdunUNRcPvHiKQmZlJShcy/DTC06mPHDniIQuQjdUJ+J1eI/oUHhvhMRJvD7YUEKWLEt6GVq+dBBtqPN9//70Qj/fff7+haPjdAALsSkb2BsAiwn+YGWdARVg0y83J3wgRkVyelOVYtCTamG07AantokSPPcwbQ3/lyhW68847pY7p5z//OZ0+fbqx6DhmAIGSkhIHrwAsIjxDDpMcDKgMC2a5KmGyEBFvd3liKwHhDaE6+dwhKtdTLkqU10CfPn3E08e8efOUh/C/yQiwdwDlAk8WEp7sgPEqk1WUCc1ZqHB58tXRz01ooWdMspWAjFEsFAxMX+8Zgopcdu/eLcTjxRdfVBzBv2YmoFzoySLCe7Rg3MrMNWYO25QuT7alLDGHUR62wjYCopyuy4+YRoSHH35YCMjRo0eNMAF5ukiAF3wq1+ywkLC7fXhMdhGoF5zGszr7731GvPE4lhPqBaV2LKItBCQ4c4uoxHGhxgxajx07VogH/49gTQK8dkfeLZJF5Gc/+xnBc7I169ITVvMYq7wtBG+Re6Xcu3YXtbyAZBQlUWffu6RK7OLbgjIve35fCH7a4M6G//gpBMHaBHgNj3IaNtfrP//5T4ITTGvXq17Ws1NWWUR4YypvCpYXkLGh74rK25+1zZC64/EOWUB4HATBHgR4OvZdd90l6pbreMyYMfYoHEqhKQF2kSSLyPbUbzVN28yJWVpAViRMEJW2ImGiIZx5ppUsHjwDC8FeBHhatnJmHdf1Qw89RAEBAfYqKErjFoGi8gLiBcuyiMTlhrmVnlVOtqyA8NOGXFnjQt81hDev8eC1Htyp8NoP7mwQ7EmAnyz//ve/i5sFrvPPP/+cLl++bM8Co1ROE4jJCRF90sCgtlRcYX/3RZYUkIyiFGJ/NCwgXXzvooyiZKcrW4sTeJW5/PTBrzsQ7E9AOVmC6/5Pf/oTrV/v+Snj9idtzRJuSVkoRGReVD9rFsIJqy0pILz6U376CM7c6kRxtYvK6wRk8eABVwTvIcCTJl566SVR/9wOPvjgAzpz5oz3QEBJGyQwO7Kn6J92pC1rMJ4dDlhOQHh7SVk8lsdPMKQOeKUye9jljoM97vKsHQTvI8DjX7/4xS+EkPD/8+dj5zrvawmOJebdDL/Y84Top+LzDjtGsNE3SwkIb+Yii8eYgx0MqwZ2dyE/ffC6AQTvJcBPHfz0IbcH/uSnk6ioKO+FgpJT9MX9oq8aFPQ8lVTac3zUMgKSdTmVuu66R6qUTj53Evu9MiKwwz25s+CVywggwAR4HITHQ+S2wZ/jxo0DHC8msDl5gRCReVEDbEnCMgIyPuwDURn7MjcbVhnstVXuJNj9BQIIyAR4RhbPzJLbB3/yzK3AwEA5Cj69jMCsIz1Ev+WTttx2pbeEgKxOnCIqYXm8cXd1vG+E3DmwAz4EEKiPAK8R4bUiclvhzy+++IKKi4vri47fbEygoDSX+gQ+Lvov3mPdTsH0ApJcGCvgjz7Y3jD2vHOd3CGwC3AEEGiKAK9al9sMf/Kq9h9++KGp03DcZgSiLuwTfdikQ5/YqnSmF5DJhz4R8I/nRxoGn7c/lTsD3kcCAQTUEGD/WexHS247/PnRRx9RRkaGmtMRxyYEeMaoPAEoMN0+a8ZMLSB70n8Q0Nldu1Fh7ty5ogPo27evUWYgXwsTYI++7NlXFhL2+LtgwQILlwimO0OgpOIK9d79sNSf9Qp40DZee00rIFcqLhGDZtVm8MUVxriMSEtLoxtuuEG68Hkvbd4OFQEEXCHAe4vwHiOyiPBnu3btKCbGXu/FXWHjDecEZfwoboi/i7PHlg+mFRAGLD/y7c3YYFj7evfdd8UFv2GDcXYYBgAZa05g7dq10q6HSiGZMMGYRbGaFw4JNkpgSngn0a8l5EU0GtcKB00pIAxWFo8p4R0N48gXunyRf/zxx4bZgYztR+DSpUvUq1cv0b64nT366KO0d+9e+xUWJRIEUgrjRN/GW1FYPZhSQNi7riwgKYXHDGFcWFhIzZo1ky5wfl+dmZlpiB3I1N4E/Pz86IEHHnAQkn79+tHVq1ftXXAvLt3a49NF/+Z7aqWlSZhOQHadWiXgrj0+zTC4yrvDhQsXGmYHMvYOAqNGjXIQkebNm9PGjRu9o/BeVsqK6nKxd8hnu+6l/NILliVgKgFhkAyUnz54c5aK6jJDwPJdofzqigc5EUDAEwQiIiLo+eefF22P2+Ann3xCWVlZnsgeeXiQQEjWDnGjvDh2qAdz1jYrUwkIg5RfXbHjRKNC69atxUUcGxtrlBnI10sJfPXVV3T99deLNvib3/yGFi1a5KU07FtspZuT6IsHLFlQ0wgIA5TFY+aR7obBVL5KmDjRmG1yDSs8MjYNgdTUVPr3v/8tRISfRl555RU6dsyYMUHTgLGRIelFSaLPG3HgDUuWzDQCwgBlATHK0y6/QpBfXfGMGAQQMJrA6tWr6fbbbxftktvnpEmTjDYL+WtEYMPJr0W/ty11iUapei4ZUwjI9tRvBcQNJ7/yXOlr5aR8/4zplLXg4KthBAoKCqhHjx4OIvL444/Tvn37DLMJGWtHYPC+F6T+r5NPMzpfbC0XN4YLyIXiDGJw/PTBII0K/N5ZfvrgaZQIIGA2Ar6+vtSqVSvRTrm9DhgwgEpLS81mKuxxgkB4tr+4gZ4X1d+JM42PariA8EYr8qurQ9n+hhDh983XXXeddGHy9EnMwTekGpCpSgIjRoxwEJEWLVrQpk2bVJ6NaGYk8PXRvqIfjDhvnf1jDBUQXiQoi8fco8Y5KVQOVmLuvRkvL9hUm0B4eDi1bdvWQUg6duxIZ8+erR0V3y1A4NyV06IvHB/2vgUs/q+JhgrI/OiBAlpaYYIh0HiQUn51xXPuEUDASgRmz54tnp65Hf/2t7+lxYsXW6kIsPV/BNYkThP9YdSFYEtwMUxAlFPY+PHNiMCDk7fddpskIDzXHgu2jKgF5OkugeTkZHrnnXfEjRALyauvvkpxcXHuJo3zPUgg9+o5ISBG+gB0psiGCcji2OEC1smCKGds1iyucmYLFmpphhUJGURg5cqV4oZIfqqePHmyQdYgW1cI8L5H8mv9uNxwV5Lw6DmGCMi5K2cEpFkGLRrkGS3yRcYLtBBAwA4E8vLyqFu3bqJtcxt/4oknKDjYGq9E7FAH7pThrGIsxKi+0Rn7DREQR5UNc8ZezeIqp0Nida9mWJGQSQjs3LmTWrZs6SAkAwcOpPLycpNYCDMaIuD4dia6oWim+N3jApJ7NVs8fRj1nk85DRKrek3RDmGETgSGDRvmICL33HMPbd68WafckKwWBM5cOin6SKPGh9WWw+MCwi7a5Xd8Rsw04OmP8qsrXs2LAAJ2JxAWFkZt2rQR7Z7b/6effkrZ2dl2L7ply6ecoXqqMNG05fCogBSVF1AnnzskATFqrrNy7jxcQZi2XcIwHQjMnDmTrrnmGiEkN910E3377bc65IQk3SWQrFgjtzDmS3eT0+18jwoI+7mSnz7CswN0K1RDCfOcefnpg11AIICAtxFISkqi9u3bi+uAr4fXX3+dEhKMWYflbfydKe+cyN6iv8y6nOrMqR6L6zEBKa0soW5+90lARoW85bECyhnxXPlrr71WunDuvvtuKiszZrMq2R58goCRBFasWEG33HKLg5BMnTrVSJOQdy0CiXlHhIAsjRtV66g5vnpMQLakLBIweDcuTwflQiv4DfI0feRnRgK5ubn02WefOYjIU089RQcOWHNzIzMydtemaYe7in7zQkmmu8lpfr5HBKSqpop6BTwkgRga7PktYnmBlfzqiv0FIYAACE4cwoEAACAASURBVPxEYMeOHXT//feLa4SvlcGDB1NlZeVPkfCfIQRickKEgKxKMN8+MB4REJ+05QJCUMaPHq0IXlh16623ShfHjTfeSOfOnfNo/sgMBKxAoKamhoYOHeogIn/5y19o69atVjDf1jZOPPSx6D8LSi+aqqweEZB+e56SAAwMauvxwitX5S5ZYr0dvzwODBl6NYHQ0FB69tlnHYSkc+fOdOHCBa/mYmThj5zfIwRk/YlZRppSJ2/dBWT3mXWi8H6n19QxQM8feDWu/Orqtdde0zMrpA0CtiIwY8YMce3wNfT73/+eli1bZqsyWqkwYw52kPrRrrtaUHFFkWlM111ARoW8LRX8i0DPL9r729/+Ji6C+Ph400CHISBgBQInTpygt956S1xDLCRvvvkmHT9+3Arm28rGsHO+4kbc38M34o2B1FVAeAWlvO5j/YmZjdmh+TGlC4cpU6Zonj4SBAFvIfDdd9/RH/7wBwchmT59urcU3zTl7BP4mNSfjgt9zzQ26Sog647PEAJy+tIJjxWaXTfIr66efPJJj+WLjEDArgQuXrxIXbp0EdcVX1/PPPMMHTx40K5FNl25VidOEf1pRlGSKezTVUDkwfPRB9/xaGH/8Y9/iIa+f/9+j+aNzEDAzgS2bdtG9913n7i+WEiGDBlC1dXVdi62KcqWUhgnBOSHk3NMYZNuAhJ9cb8orO+plR4rLPv7kZ8+Bg0a5LF8kREIeAuBqqoq+vLLL8V1xtfbX//6V9q+fbu3IDCsnCMOvCH1q0bMaK2v0LoJCDsAk8c/PDV3+eTJk6JR33vvvVRRUVFfmfEbCICABgRCQkLo6aefFtccC0nXrl0pJydHg9SRRH0EdqQuFf1qXK4xeykp7dJFQMqrSqmz711SQWcd6aHMT9f/3377bdGYt2zZomteSBwEQOC/BKZNmyauOxaRm2++mZYvXw48OhDIKTkrBGTJsRE65OBckroIyL7MLaKQoWd9nbPIxdjsHE5+ddWpUycXU8FpIAACrhBITEykN954Q1yDfC3yDR2/FUDQlsC0w12k/pWd07KbKCODLgIy9fCnUgG7+91PNVSje/n4kZnverjR8h4H58+f1z1PZAACIFCXwNKlS+l3v/udg5DwuCSCdgT2Z20TN+ghZz3vmFZZEs0F5GJJpijc0mOjlXnp9j+/d5WfPrgBI4AACBhHgG/g+C2AfE3yJ8+M5On1CO4TqKguJ16RzmPMMyO6uZ+gGyloLiDbUpcIAUnIO+yGaepOZU+ickPljXEQQAAEzEGAxyF5Mot8ffInL/Blx40I7hFYHDtU9LP5pca9cdFcQIbtf1Uq2OB9z7tHSMXZ3BB5+qDcQPk9LAIIgIB5CPBMSJ5OL1+j/MkuhvjGD8F1Ako37+zt3KigqYAkFcQKVdyYNFf3MvECJrlh8kwQBBAAAXMS4AW97BVCvl75kz1l86ZWCK4R6L/3Gam/ZX+DRgVNBYQ3PJHXfui9hy+7nZYbI++ihgACIGB+AuyXTr5u+ZO31eUZlAjOE2DX7nJ/y34HjQiaCsjnux+RCjQ+7APdy8J+eOSGyAuaEEAABKxBgD1j8/YK8vXLn+3bt6ekJHP4d7IGRSL2LygLyLrjxji31ExAlJueBJxZp2sdKPcq4K03EUAABKxHgDd442n3spBcc801NGuWuTZMMjvVMQffkUSk7x5j3sJoJiDzovoLNbxcXqgbd96jQG5wvOUm++VBAAEQsCYB3mK6Y8eO4prma7tNmzZ06NAhaxbIw1azn0H5KYT9D3o6aCYg3fz+KhVk7tEvdC0Db2gjCwj2a9YVNRIHAY8R2LRpE91zzz3i2uZrfPjw4R7L36oZsZ9BWUBWJkzyeDE0EZCkghhRCN7CVq/AG9vI4sH7NCOAAAjYh0B5eTkNGDBAXON8rbds2ZJ8fHzsU0gdSiLv+spLKDwdNBGQrSk/LR7MvJyiSxl4Qxvel5kbFX9euHBBl3yQKAiAgLEEgoOD6YknnnAQku7du1N+fr6xhpk097XHp4sb+PzSix61UhMBkX1f6TmQo9wNbdmyZR6FhMxAAAQ8T2Dy5MkOInLbbbfRqlWrPG+IyXOMuhAsBIT3TvdkcFtA2Flil/+5bl8Qo8+MKN4FTX51xWMgCCAAAt5BIC4ujl599VVx/XM/0KFDB0pJ0edNhxWpllaWCAFZFjfGo0VwW0AS8iKE8UEZmzQ3nmdZ8WwrWUCOHz+ueR5IEARAwNwEFi9eTL/97W9FP3DdddfRnDnm2NbVDOTGhb4n9cOD973oUXPcFpAfk+YLATlfnK658cqtM6dPN2axjOaFQoIgAAJOEzh79iz95z//ESLCN5XPPfccHT6sv9NWp4318Am8R7o8G+tiSZbHcndbQCaEfSgZPjDoOc2N5hXm8pMHrzxHAAEQAIEff/yRWrRoIfoG7iNGjhzp1WCO5YYKAQnO3OoxFm4JSHlVmTBaj+0V2ceVLCAHDx70GBRkBAIgYG4CpaWl1L9/f9E/cD/RunVr2rVrl7kN18m6yuoK6uTTTOqP2dW7p4JbAqJ0KRySpa17ZuU+y+x1FwEEQAAEahMICgqixx57zEFIevbsSYWF+nnDqG2DWb5PPvSJJCD99z7rMZPcEhClN8i8q9maGc37eshPHrzfR3V1tWZpIyEQAAH7EZg4caLoM7jvaNasGa1Zs8Z+BW2kRJuTF4g3QmevnGokpnaH3BKQMQc7SAYPCW6nnUVE9MYbb4jGsH37dk3TRmIgAAL2JBAbG0v/+te/RN/BQvLuu+9SWlqaPQtcq1TH8yOFgOxJ/6HWUX2+uiwgJRWXhbHL48drZh3vaS4/ffBe5wggAAIg4AyBhQsX0q9//WvRj9xwww00d67+G9w5Y6Necbvuukfql+dHD9ArC4d0XRaQyPN7hYAcyvZ3SNTVL+fPnxfunW+++WbKyclxNSmcBwIg4MUEMjMz6eOPPxYiwjelL7zwAh05csTWVKZHdJX65T6Bj3mknC4LyOrEKUJALpVp46OmU6dOosKXLzdun1+PkEcmIAACuhPYsGED/fnPfxb9CgvJ6NGjdc/XqAx2pC4V/XJ6kf4bdLksICMOvCEZOvLAG5qw2rJli6jkt982bo9fTQqDREAABExDoKSkhPr27Sv6FxaRBx98kPz9tXlzYpqCElFK4TEhIH6nV+tumksCUliWJ4zkJxF3Q0VFBd17772igk+ePOlukjgfBEAABBwI7Nmzhx555BHRz7CQ9O7dm4qKihziWf1LD/9WUv88J7K37kVxSUB4zENeNh95IchtIwcNGiQqdebMmW6nhwRAAARAoCEC48ePF/0Ni8gdd9xB69bpt49RQ3bo9fvsyF5S/9wroLVeWYh0XRKQzckLhYAUlOaKxFz5Z//+/aIy//GPf7iSBM4BARAAAacIREdH08svvyz6HhaS999/n06fPu1UOmaMvCVlkeif80v13TfJJQFZED1YMrCnfyu3+T355JOiEsPCwtxODwmAgDMEeMXyvHnzpBk63InIf7/73e/onXfeIb7BQbAvgW+++YZ++ctfinr/+c9/LrUHK5c4PDtACAh7S9czuCQg8haKYw6+45ZtU6ZMERU3bNgwt9LCySDgLAFepMpCIYtGQ5+8mRmCfQmkp6fThx9+6NAOXnzxRYqMjLRkoXn2lTzEoPeCQpcEpLv//ZKBC2Nc91EVHx8vKuz++++3ZEXBaOsSUO69fdNNNxG/F+enDX4iOXPmjLTzXfPmzUUb5fgI9ibw/fff05133inqnG8oxo4da7lCV1SXCwFZnThVV/udFhB+pyar29aUxS4b99prr4mK2rlzp8vp4EQQcJbA119/Ldpe+/btG3S8x2Ly/PPPi7h4neUsaevFv3LlCvXp00fUOYvIww8/TAEBAZYqzICgNlI/PSPiM13tdlpAEvIOCwHhd22uhCVLlogK6tatmytJ4BwQcIkA+0uSX1Vxx9CU11Y+LsdnsUHwDgK7d++WhEOue/78/PPP6fLly5YAMO1wF6mfHqTDPk1KAE4LSGD690JAMlxY6Xju3Dm68cYbpYvylltuoby8PKU9+B8EdCUgP1Hwa6umxEM2pHPnzlJ75fESBO8iwK+wlCLCr7jWr19vegirEiaLfrqyulI3e50WEKULE37X5mzo2LGjqJCVK1c6ezrig4DLBJRPHzzmoTYo1w1wGgjeReDo0aPEg+pKIfnggw+ksTKzkth9Zr0QkMzLKbqZ6bSA8Ds1HgMZENTWaaM2bdokKgGvA5zGhxPcJKAcOFf79MFZKtcqYRzEzUqw8Ok83Zun+cpC8otf/ILmz59vyhLF5YYLAYk4H6ibjU4LCO99zgLCXh+dCeXl5XT33XdL8K+55hpKTk525nTEBQG3Ccizqpy9eeHpvnKnAQFxuxosnQDP0OMFh3J74M+XXnqJoqKiTFUu3uBPnuy0LXWJbrY5JSC8765s1KrEyU4Zpbz7mzVrllPnIjIIuEtA+fqKZ2E5E5SvsCAgzpCzb1weB2EXKEohGTdunKkK3M3vPqm/1nOPdKcEJKMoWQhI4Bn1A0nBwcECdJs2bUwFGcZ4BwF3XkMpBcSZV1/eQdZ7S8kzsnhmllJE/v73v1NgoH6vjJyhPSrkLam/Hhf6rjOnORXXKQE5nL1bCEh87mHVGT3++OMCcnh4uOrzEBEEtCKwatUq0QadfYrgV17cSfDMLQQQqE2A14g89NBDon1xW/niiy+ouLi4dlSPfp8fPVDqr3sFPKhbvk4JyLaUJUJA8q6eV2XUpEmTBNjhw4erOgeRQEBrAu48RbBwcKfg7NiJ1mVAeuYmMGbMGNHXcXu566676IcfPLM3eX1kNiV/I/prrTb9q52PUwKyKGaoZFA3v7/WTqfe73FxcQJoy5Yt642DH0HAEwSUAuJMfspXX86OnTiTD+LagwD7z/rnP/8p+j0Wko8++ogyMjI8XsCwc75CQE7kH9Ulf6cEZGxoB8kgfremJrzyyisCpI+Pj5pTEAcEdCGgFBBn1nLIr6+4I+AZOAggoIYA32z87Gc/E/3fr371K1qwYIGaUzWLc6owUQhIUMYmzdJVJuSUgPQMaC0Z9E30IGUa9f6/aNEiAa979+71xsGPIOApAsonCR4PURNYMFg4+I9XoyOAgDMETp06Re+9955oQ9yO2rVrRzExMc4k43Lc0soSISDrjs9wOZ3GTlQtIMptbDcnN66kZ8+epd/85jcSuNtuu43y8/MbswHHQMAjBOSxjBYtWjSZH8+24hk1fNHzeXj6aBIZIjRAYO3atfTHP/7RQUgmTJjQQGxtf+6352lJRGZH9tQ24f+lplpAlFN4gzO3NmrMJ598ImCpvdtrNEEcBAENCChfYzW2x4dSPFhA0IY1gO/lSVy6dIl69eol+kVuV48++ijt3btXVzLjQt+TBMTdvZsaMlK1gCQVxIjHIZ7O21D48ccfBaQOHTo0FA2/g4DHCbAwsAdevnj574UXXqAdO3YIO3hshO8MlZtMQTwEHvyjAQE/Pz964IEHRBvkdtivXz+6evWqBqnXTUL2yjsk+OW6BzX4RbWAxOYcFALC/9cXSktLSXYXcd1111FKin5OvOrLH7+BQFMEaouILCa1P/m1FbswQQABPQiMGjXKQUS439y4caPmWc092lfqt/lVlh5BtYAo99nlp5H6AiupfCHOmTOnvij4DQRMQYCfLGTX7nKblT/Z7Q4LDQII6EkgIiKiThvk1/9ZWVmaZbs4dpgkID38W2mWpjIh1QISnLlFPIHweEjtEBQUJMTjueeeq30Y30HA1AT49ZU8yN7Y+IipCwHjLEngq6++ouuvv170nzwBiWexahFWJkyS+u1OPndokVydNFQLiN/pNUJAckrO1kmIB4TkO7jDh9W7OamTEH4AAYMIKLe6xdiHQZXgpdmmpqbSv//9b9GHcl/K6+iOHTvmFpENJ78S/XZ5ValbadV3smoB4f3PZU+8l8sdH+8nTpwoCj5y5Mj68sFvIGAJAvJrLR5Id2bBoSUKByNNT2D16tV0++23i/6UhYTdQbkatqcuFf02L8XQOqgWkPUnZglD2K27HPgik588WrduLf+MTxCwJAFe7yG/yuL1IhgLsWQ1WtrogoIC6tGjh+hXuX9lh7T79u1zuly7z6wT/fb54nSnz2/qBNUCsjx+vGRIF9/mDmnyykpZQHbt2uVwDF9AwIoE5AF2fhqB/ysr1qA9bPb19aVWrVqJ/pX7WZ7gUVZWprqAB7K2CwE5femE6vPURlQtIAtjvpQM6RXwkEh74cKFonA9e+qz0lFkhn9AAARAwAsJjBgxQvSzLCK8sytvD64mHDm/RwiIHg4VVQvInMjekiH99z4r2Z2ZmUnsIIwL1KxZMzzqq6lNxAEBEAABFwjwPkpt27Z1EJKOHTsSu41qLCj3Ro++uL+xqC4dUy0gU8I7SgIybP8rUkbsolh+dbVmzRqXMsdJIAACIAAC6gnMnj2brr32WtH33njjjbRkScN7nqcUHhNPIGHntB9iUC0g7EuFZ2Gxb5UNGzaIArz7rn7bJarHipggAAIg4B0EkpOT6Z133hF9MN/Iv/baa8T7L9UOWZdThYDo4dJdtYAMCW4nGTJxf0dppy02+oYbbqC0tLTaNuM7CFiKQE1NDR06dIhOnjxpKbthrHcTWLlyJd16660OQjJ58mQHKHlXs4WA+J5a6XBMiy+qBUR2C/yPDx4UBs+dO1cLG5AGCBhCICcnh/r27Svas/xKdtmyZYbYg0xBwFkCeXl51K1bN4c2/OSTT1JwcLCUVHHFZSEgTW3D4WzeHF+1gPT0b0UvTfyDMJQ9mSKAgFUJsHjccccdoj3L4iF/suttBBCwCoGdO3fS3/72N4f2PHDgQCotKxUCosemUqoFpJPPnfT7u3/aovHIkSNWYQs7QaAOgfqePGTxkD/5tRYCCFiJwLBhwxxE5J577qF/jmwmich3cWM1L4oqAWEfKg9+9Fth2OjRo2nGjBn4AwNLtoHp06eLtiyLRX2fTz/9tCXLh2sTfdM//vEPhzZ+9z9/RWq2IndWYVQJyKWyfPrZb65zMKi+Cw6//XejInAAB7QBtAGztYFu819zVh+ajK9KQIoriujRz26EgPxvJzuzNQzYg84KbQBtoLE2cP3Pr6Wvjn7epCA4G0GVgFTVVEnv0N5bezMtDh1LFy9exB8YWLoNNHaxycfGjkVbx7Vu/b7u0w1/o48330yLY4c6qw9NxlclIJxK1133/G8gZlyTiSICCJidAE/VlYWivs9f/OIXdOnSJbMXA/aBQJMEOvv+Seq7VyRMbDKusxFUC0jv3Q9LRiyIGexsHogPAqYkwFN1GxKP9evXm9JmGAUCzhCoqC6T+m32IvLDydnOnKoqrmoBGRjUVjJkdiS87qoii0iWIMBTdXv37i3NoX/iiSekWVdFRUWWsB1GgkBTBIrKC4SAbEtt2GdWU+k0dFy1gAw/8LpkyOTwTxpKC7+DAAiAAAiYiMCFkkwhIAFn1mpumWoBGR/2gWTI6IPtNTcCCYIACIAACGhPIL3opBCQ/VnbNM9AtYBMj+gqGfJl8EuaG4EEQQAEQAAEtCdwsiBKCEjE+d2aZ6BaQOZF9ZMM6bvnSc2NQIIgAAIgAALaE4jJCRECciw3VPMMVAvIkmMjJEO6+7fU3AgkCAIgAAIgoD2BQ9n+QkCSC2M1z0C1gKxOnCIZ0smnmeZGIEEQ0JNAYWEhxca6d/Hw+e6moWcZkTYI1EdgX+ZmISCZl1Pqi+LWb6oFZGPSXGFIWdVVtzLFySCgN4FVq1YRbzlQe51HixYtaMKECaqyZ8GovfMbp8e/QUxUIUQkgwnsOr1K9Nu5V89pbo1qAdmZtkwYUliWo7khSBAEtCDAHTuLhFI4brrpJmrevLnDb3//+9+Jn0waCixAjaXxu9/9jrZv397Q6fgdBExBYEvKItFvX6nQ3rOCagEJTP9eGJJdfMYUcGAECNQm8PDDD0sdPwsGi4BSJPj/8ePHC2Ho3Llz7dOl72fOnCEWCBYQTo+/y4H/b9++vXSM4yiPyXHwCQJmIbD+xEzRb1fVVGpulmoBOXh2pzDk9KXjmhuCBEFACwLcoQ8YMMBBOGqny8flpwulwMjxWFj4OItQfcc5nixUDYmQnBY+QcBIAsvjx0n9dtddLXQxQ7WARF7YKwTkeH6kLsYgURDwBIH9+/cLAeH/awdZXPgJpqGgfMXVkMg0dC5+BwFPEWDfhewHi30Z6hFUC0h83mEhINEX/7thux4GIU0Q8AQBWSRqC4hSXJoSBjkNjIV4osaQhysE2HchC8iAoLaunN7kOaoFJLUwXghI2LldTSaMCCBgVgI80C53/rVnU8ljJPz6qqkgv8bicxBAwIwEJof/R+q3hx94VRfzVAtI1pU0ISB70zfqYgwSBQFPEPj6668lAeHZWbWDPD7y/PPP1z5U5zvHYSHiQXUEEDAjAfZdyE8g48Pe18U81QJSUV0uBGRN4jRdjEGiIOAJAvKU3vqeHGRRUCMg8tOKmrieKBfyAIHaBLr73y/12wtjvqx9SJPvqgWEc+u/t41kzMyIbppkjkRAwNME5E6fnz7qG+OQBUTNU4WcFgTE07WI/NQQyC+9IG76t6YsUnOK03GcEpBph7tIBg3a1/TjvdOW4AQQ0JmAcuZUQwPfsoDU93RS2zwISG0i+G4mAgl5EUJAwrMDdDHNKQFZmTBJGFRVU6WLQUgUBPQgwIPl8uJAHudoKMgCouapAgLSEEX8bgYCe9J/EP11elGSLiY5JSC7z6wTBunhmEuXEiJRryegFI+mFv45IyDODLh7fSUAgMcJrE6cKvprHsPWIzglIHG5YcKgiPOBetiDNEFAUwLOiAdn7MxThSw2asZLNC0UEgMBFQRmRHwm9dcDgtqoiO1aFKcEJO9qthCQ7anfupYjzgIBDxFwVjzYLHmKL7/uaio0NpurqXNxHAT0JjAo6Dmpv552uKtuWTklIGxFN7/7JKMWxw7TzSgkDALuEnBFPDhPPk9eZNiYo0SewSXHa2hA3t0y4HwQcJVAZXWluNlflTDZ1WSaPM9pARkZ8qZk2LjQ95pMHBFAwAgCroqHbKuaJwv5SYVFpL7pwHJa+AQBIwjwGDUvIOS/3WfW62aC0wIyP3qAZFSvgId0MwoJg4CrBNwVD85XFgd+jVWfOPBv8oyupgblXS0HzgMBdwjwGLUsIHG54e4k1ei5TgvIpqT5wrBLZfmNJo6DIOBJAvzKSe7Y+ZN3HlTzV9+rKtnPFW9OtXr1alEMfl3Fm1HxkwcvRqzvXBEZ/4CAQQS2pS4R/TSPXesVnBaQ0LO+wrCT+VF62YV0QcBpAkpPuvL4hJrP2h55OWMWBllE6kuDxYOfdhBAwIwEFscOlfrpbn5/1dU8pwXkVGGiEJCgjM26GofEQcAZAtyh89RaZ/8aEgJ+VcWvs5RCwv/z+g88eThTM4jraQLjQt+V+ulRIW/pmrXTAlJaWSIEhLdLRAABEAABEDAXgV4BD0r99Pzogboa5rSAsDX99jwlGceblSCAAAiAAAiYhwCPTcsD6JuSv9HVMJcEZEp4R8nAL4Nf0tU4JA4CIAACIOAcgRP5R4WAhJ3zde5kJ2O7JCDL48dLBnbyaeZkdogOAiAAAiCgJ4GgjE1CQHjMWs/gkoD4nV4tDDx75ZSe9iFtEAABEAABJwisOz5D9M88Zq1ncElAjudHCgPZZTACCIAACICAOQiMOdhB6p+HBrfT3SCXBISt6rrrHsnIeVEN762gu/XIAARAAARAQBAorrgsbu55qEHv4LKATI/oKhnaJ/AxvW1E+iAAAiAAAioIRJ7fKwTkULa/ijPci+KygOxIXSoMTS866Z4VOBsEQAAEQMBtAqsTp4h+2ROuplwWkJTCY8JQHlRHAAEQAAEQMJbAiANvSP3yyANvesQQlwWErevh30oydk5kb48Yi0xAAARAAATqJ1BYlidu6nk7W08EtwRkdmQvyeCeAa09YSvyAAEQAAEQaIDAoXN+QkAiLwQ1EEvbn90SkF2nVwmDUwvjtbUMqYEACIAACKgmsDx+nOiPSyquqD7PnYhuCciZSyeEwTvTlrljB84FARAAARBwg8CQ4Jel/nhsaAc3UnHuVLcEhLPqs/tRyegZEZ85lzNigwAIgAAIaEIg9+o5cTP//YlZmqSpJhG3BWReVH/J8M/87lWTH+KAAAiAAAhoTOBA1nYhILE5BzVOveHk3BaQwPTvheHYobBh0DgCAiAAAnoRWBI7XPTDFdXlemVTJ123BSTrcpowfEvKojoZ4AcQAAEQAAF9CQwMaiv1wxMPfaRvRrVSd1tAOL3+e5+RjOd9QhBAAARAAAQ8RyC7+Iy4id+UNN9zGRORJgKyMGaIVIBOPndSVU2VRwuAzEAABEDAmwkEZfwoBCQx74hHUWgiIPsyt4gCxOWGe7QAyAwEQAAEvJnAN9GDpP63i29zj2PQREAuFGcKAdmYNNfjhUCGIAACIOCtBPrueVLqf6ce7uxxBJoICFs9eN/zUiFGhnjGiZfHSSFDEAABEDAZgaSCaHHzvi11icet00xAvj8xWxQEbk08Xo/IEARAwAsJrEiYKPpdnhHr6aCZgPCeIB133ir9rT0+zdPlQH4gAAIg4HUEeu9+WOpzJ4R9aEjZNRMQtn7s//bi/SLwSUMKg0xBAARAwFsIRJwPFDftgenrDSm2pgKi9M4bdSHYkAIhUxAAARDwBgJfR/UTAnKlosiQImsqIMoNTRZEDzakQMgUBEAABOxO4ErFJSEeLCRGBU0FhAshbzLVyecOKq0sMapcyBcEQAAEbEtg95n1QkD4VZZRQXMBCTu3SxQsKGOTUeVCviAAAiBgWwI8aM6TlngQ3ciguYBwYXr4t5QKB99YRlYt8gYBjWloZwAAFcdJREFUELAjAaUD25UJEw0toi4CsixujHgKOV+cYWgBkTkIgAAI2InAj0nzRf+aVBBjaNF0EZDEvAhRwK0piw0tIDIHARAAATsRGLzvBal/Hbb/FcOLpYuAcKkG73vxf4X8l+GFhAEgAAIgYAcCZrs5101AHB+zou1QdygDCIAACBhKQDk8cMEEwwO6CYhyoIf9tSCAAAiAAAi4R6C7ySYo6SYgjMksU83cqzKcDQIgAALGE3BcIrHZeIO02pGwoZKwfxbZwaKRi10asg+/gwAIgIBVCMyO7Cn1p7zza1nVVVOYresTiMNy+6N9TVFgGAECIAACViNQWJYjbsYXxJjHTZSuAsKVpHT4ZYS/eqs1FNgLAiAAArUJbDz5tRCQ6IvmcVSru4DwJu/yayyeQYAAAiAAAiCgngD7FOzm91epHzXbjq+6Cwhjmna4ixCRiyVZ6skhJgiAAAh4OQFejC3fhB/I2m4qGh4RkJicEAFgVeJkUwGAMSAAAiBgVgJVNVWSw0QWkCHBL5vOTI8ICJd64qGPJBH5dOftVFCaazoQMAgEQAAEzEbA99QKcfO9N2OD2cwjjwlIxPk9AsT6E7NMBwIGgQAIgIDZCPTb87TUbw4IamM20yR7PCYgnNvog+9IMLruuoeKDdqC0ZS1AKNAAARAoBYB5aZRfqdX1zpqjq8eFZDQsz7iKWRT8jfmIAArQAAEQMCEBGSvu30CHzOhdf81yaMCwlkO2/+qJCI9/R+giuoy04KBYSAAAiBgFIF9mVvEzfaO1KVGmdFkvh4XkH2Zmy0BpklyiAACIAACOhEYfkC+0W5FFdXlOuXifrIeFxA2+adHs8fdLwFSAAEQAAEbEQg96ytusjeb/FW/IQKy+8w6Acisg0M2ao8oCgiAgIUIjHGYbHTZ1JYbIiBM5KfpaW1NDQjGgQAIgICnCLDXcnnVuRWWOxgmIL6nlgtQe9M3eqp+kA8IgAAImJaAvOC6o0UWXBsmII5L9NuZtkJhGAiAAAh4gkBMzgFxU20Vl0+GCQhXyJaURQKY2ZyEeaLBIA8QAAEQkAlY0emsoQKidFM8YG8b4qcSBBAAARDwNgJh536aeWWlbS8MFRBuJD5p34mnECsMGnlbw0Z5QQAE9CVQXVNFA4LaSv1gF9+7KKfkrL4Zapi64QLCZRl9sL0QkVOFiRoWD0mBAAiAgLkJ8I2zPPNqZ9p35ja2lnWmEJBjuWECIL8HRAABEAABbyDAN8yyeIwKedtyRTaFgDC1b4+NFCDZDwwCCIAACNidwPSIrqLfO5YTarnimkZALpXlU3f/lhJM9j7JA+wIIAACIGBXAsEKh4l8A23FYBoBYXgBZ9YKNV6VgK1vrdigYDMIgEDTBMqqrlKfwMel/q67//1UWJbX9EkmjGEqAWE+E8I+FCKSVBBtQmQwCQRAAATcI8ALBeWxD/8za91LzMCzTScgJ/KPCrATD31sIBpkDQIgAALaE0gqiBF93PiwD7TPwIMpmk5AuOwrEiYKwLytIwIIgAAI2IXApEMfi/6Nb5itHEwpIFcrr9Dnux+RIPPOhUXlBVZmDNtBAARAQCIQmL5eiMeKhAmWp2JKAWGqQRmbBGgrLe23fItAAUAABHQhcLm8kHoGtJb6Nb5BLqm8oks+nkzUtALCEKYe7ixEJD433JNckBcIgAAIaEqAb4TlgXO+QbZDMLWApBbGC+BjDnawA2+UAQRAwAsJxOcdFn3Z1MOf2oaAqQWEKa87PkOA9z21wjbgURAQAAHvITA2tIPox/jG2C7B9AJSWV1B/fc+I+AnF8bahT3KAQIg4AUElM4S1x2fbqsSm15AmHZ4doAQkOEHXqWqmkpbVQIKAwIgYE8Cyr5r2P5XqLLaXn2XJQSEm5ZSxRfHDrdna0OpQAAEbEPgYkkW9Qp4UNz8JhXY7+2JZQSEW9WU8I6iMrDA0DbXGQoCArYkoJxF6n/auu5KGqscSwnIheIM6uHfSohISmFcY2XDMRAAARAwhMAPJ+eIfmpR7FBDbPBEppYSEAZy6JyfqJgRB96g6ppqT3BCHiAAAiCgikDE+UDRRw3d/y+qqC5XdZ4VI1lOQBiycmqvVf3oW7GxwGYQAIHGCeRePUe9Ah4SAmJ3j+KWFBCuwsmHPhGVtCf9h8ZrFUdBAARAwAMEeEtuebW53+nVHsjR2CwsKyDZxenEG7HIlZVmo8U5xjYJ5A4CIOAKgQ0nvxL90cKYL11JwnLnWFZAmHTYuV2iwkaGvEk1VGO5CoDBIAAC1idw5Pwe0RcNCX6ZyqvKrF8oFSWwtIBw+dYeny4qbmncKBVFRhQQAAEQ0I5A3tVs6r37YdEPncyP0i5xk6dkeQFhvrxzofwqa2/6RpMjh3kgAAJ2IjA9oqvof3adWmWnojVZFlsIyLkrp6mb319FJZ4qTGyy4IgAAiAAAu4S2Jg0T/Q7C6IHu5uc5c63hYAw9dCzPqIiR4W8ZbmKgMEgAALWIhB5IUj0OV8Gv0TlVaXWKoAG1tpGQJjFmsSpokLnHv1CAzxIAgRAAATqEkguPEaf7bpX9DdW39u8bgnV/WIrAeEi82Yt8njI0mMj1VFALBAAARBQSYBfmX+x5wnRz/ieWqnyTPtFs52AXK0splEhb4vKXX9ipv1qDSUCARAwhMClsnwatv9fon/5MWmeIXaYJVPbCQiDzbl6lgYGtRWVvD31W7Pwhh0gAAIWJVBVU0UTwj4U/cqKhIkWLYl2ZttSQBjPmUsnqGdAa1HZe+HuRLtWg5RAwAsJzI7sKfqTb6IHeSGBukW2rYBwURPyIujTnbeLSj+U7V+XAH4BARAAgSYILI4dJvqRGRGfNRHbew7bWkC4Gg+f3y0qngfX43LDvKd2UVIQAAG3CShnd44N7eCV03Ubgmh7AeGCB2VsEiLS3b8lpRUmNMQDv4MACICAILAlZaHoOwbve5HySy+IY/iHyCsEhCt6Z9oy0RD6732WLpRkov5BAARAoEECAWfWiT6j9+5HKKMopcG43nrAawSEK/j7k7NFgxh54A0qrijy1npHuUEABBohoPRs0dn3T+StCwUbQSQd8ioB4RJ/FzdWiMjk8P80xQfHQQAEvIxATM4B0UfwuCm7LEGon4DXCQhjmBfVTzQQuDypv2HgVxDwRgK1XZTsz9zqjRhUl9krBYTpTAnvJEQELk9UtxdEBAHbEmAXJX33PCn6BW92UaK2kr1WQK5WXnFwebIoZohaZogHAiBgMwL85KEUD3bTjtA0Aa8VEEaTU3KWePtJ2fnirCM9qLK6omlqiAECIGAbAjzmofSsCxcl6qvWqwWEMRWU5tK40PeEiIwPe58Ky/LUE0RMEAAByxJQzrbiG0k8eThXlV4vIIyrorqcZh7pLkRkaHA7yrqc5hxJxAYBELAUAeU6DxYPjHk4X30QEAWzhTFfChHpE/gYJRXEKI7iXxAAAbsQUK4wZ/HAbCvXahYCUovbyoRJQkS67mpB0ReDa8XAVxAAASsTUPq24kWCWOfhem1CQOphtyn5GyEifHcSkrWjnlj4CQRAwGoElF512T0JVpi7V4MQkAb4+Z1e7SAifqfXNBATP4MACJidAG8GpdzPgx0jwreV+7UGAWmEYUjWdgcR2Zz8TSOxcQgEQMCMBHgbWuVOguySHV51takpCEgTHKMuBlMX3+ZCSFYlTG7iDBwGARAwCwFeXa7cw5w3gyqvKjWLeZa3AwKiogqTCqKJZ2XxeAj/LcSqdRXUEAUEjCXAq8u/2POEuG6xDa329QEBUcmU14U4rlrvTpfLC1WejWggAAKeJMAzq7C6XH/iEBAnGBeU5TisWu+/9xmKzTnoRAqICgIgoDcBXk0uvy3gzx/h10o35BAQJ9HyqvWvjn7u0EC3pix2MhVEBwEQ0JpA3tVsmh7xmcO1idXlWlN2TA8C4shD9bdtqUscGuqcyN5UVF6g+nxEBAEQ0I7AkfN7qPfuh8U1+eW+l+h4fqR2GSCleglAQOrFou7HY7mhxPury4/L/fY8TTE5IepORiwQAAFNCGw4+ZW4BvlaXBA9mMqqrmqSNhJpnAAEpHE+TR69UnGJeFdDWUT4k/3sIIAACOhLIPfqOZp2uIvDted7apW+mSJ1BwIQEAccrn/ZnvqtQ0PmVa9wC+86T5wJAo0RiDgfSL0CHhLXHM+QPJEf1dgpOKYDAQiIhlDjcsNpYFBb0ah5Dnr0xf0a5oCkQAAEfjg5R1xj/MTPXrTLq8oAxgACEBCNoRdXXKZ5Uf0cGvjm5AUa54LkQMD7CFwsyaKphzs7XFvssw7BOAIQEJ3Y70hb5tDQebtc3v0QAQRAwHkC4dkB1CvgQXFNDd3fjthDBIKxBCAgOvKPzztMg4KeF42+T+DjFHVhn445ImkQsB+B70/MEtcQv7JaFDNU2kXUfiW1XokgIDrXWUnlFZoXNcDhAlgeP4FKKq7onDOSBwFrE+AbMPacq5zh6H96rbULZTPrISAeqlCftO8cLgRe9BSU8aOHckc2IGAdAuxjblncGIfrZdj+Vyi5MNY6hfASSyEgHqxo3mN90qFPHC6MKeEdKaUwzoNWICsQMC+BwPTvqWdAa4drZN3x6VRZU2leo73YMgiIAZXPF4lyQJAf0dcen4b3ugbUBbI0B4H/3lx97CAcUw9/SqmF8eYwEFbUSwACUi8W/X/kx/Tv4sY6XDDsCoV3QUQAAW8hwC5HViVOdrgOPt/9CAVlbPIWBJYuJwTE4OpLkAYK33W4gGYd6U7pRUkGW4bsQUBfAsGZW4hnJioHyVckTKCrlZhgoi957VKHgGjH0q2U2O20cgMcvqjYSRwCCNiNwKlLiTQ9oquDcIwP+4BO5B+1W1FtXx4IiImqOL/0Ai2OHepwYQ3e9wKFZ/ubyEqYAgKuEaiuqaL1tdZ0dPe/n/zPYGqua0SNPwsCYnwd1LEg+uIBGnHgDQch+fpoXzp35XSduPgBBKxAIOycLw1Q+InjJ+xvj42kS2V5VjAfNjZAAALSABgz/MybVnXyaeYgJGsSpxG7sUYAASsQ4Juh2i7XR4W8TbyXDoL1CUBATF6H54szaF5UfwcR4bu35fHj8URi8rrzZvPY3frEQx85tNsuvnfRzrTvvBmL7coOAbFIlfIFOT7sfYcLkoVkcexwSi86aZFSwEy7Ewg960NjDr5Tp53yynI8Oduv9iEgFqvTqIvBxKvXWTyUf/OjB1Jy4TGLlQbm2oXAvszNNPzAqw5tsuPO22lVwmS6WJJpl2KiHLUIQEBqAbHK1/jccOL1IkoR4f/nRPamxLwjVikG7LQ4gd1n1hPPFFS2w667WkizrQpKL1q8dDC/KQIQkKYImfw474nwdVRfhwuYL2aeZx+TE2Jy62GeFQlU1VSR76kVxJ4TlMLR078VbUr+hooriqxYLNjsAgEIiAvQzHjKqcJEWhgzxOGC5ot74qGP6cj5PWY0GTZZjEBpZQltTVlM7ElaKRx9Ah+j7alL4cvNYvWphbkQEC0omiiNrMuptLSWK2y+2Mcc7EA8Fx8BBJwlUFiWQxtPfk3d/P7qIBwDgtoQtpR1lqa94kNA7FWfojQXSjKlAUzlnSL/z3eLqxOnwIW8IIV/GiIQdm4XzY7s6SAa3IaGBL9Me9M3NnQafvciAhAQm1c2D2Sy+wge2KwtJrzafUfqUsopOWtzCiieWgKJeRHSZk7d/VvWaS8jQ96kA/AWrRalV8SDgHhFNZM0sOl/eg2NC32vTsfAwsKrhfdnbcN7bC9pD8piZl1Oox+T5teZTcXtopPPnbQgejDx9HEEEKhNAAJSm4gXfM8oSpY8/Q6s5ZuIOwx+UmGHjpjBZe+GcKXiEvEU3AlhH9Z7Q8FrjXhPDh44RwCBhghAQBoi4yW/x+WG0ZJjI6ib3311OpL+e5+RXn+dvnTCS2jYv5js0eDrqH516ppvHnjfcZ5lxe5zEEBADQEIiBpKXhCH5/YfPLuTZkZ0q7dzYfcUvGcJFodZrzHwWqEVCRPrTL9l0eApuXyM4yCAgLMEICDOEvOC+Pml58knbTmx11TuZGr/8e9rj0+nqAvBeMVhwvaQXXyGgjJ+pG+iB1HfPU/WqT+uT34K4acRBBBwhwAExB16XnAuL1Bcd3w69d3zVL0dEXdGPDD/w8mvJBfdldUVXkDFXEVkJ4U8O4oda9Y3riXfAPB4R2D6erqCleLmqkALWwMBsXDledr06Iv7aWXCJBq2v7bTvJ+eUnj/ksnhn9Dm5AV0PD/S0yZ6RX6FZXkUds6PlsePk9ZkyAJR+7OLb3Oaergz8b4yWVfSvIINCulZAhAQz/K2TW48FsIr29lN9+B9Lzb4dNJ11z2SXy5eb5ICb8Eu1X9xxWWKPL9XWgBae6fK2qLBe3BsSppPvJ6jhmpcyg8ngYBaAhAQtaQQr1ECOSVZtD9zqzQFuP/eZxsUlB7+rWh2ZC/akrKIwrMDKL0oCWtPFGQvleXTifyj0hTadcdnSC5oaouE8vvY0A70/YlZ0rTriuoyRUr4FwT0JwAB0Z+xV+Zw9sop2pP+A82PHiC5T1F2evX9P2BvG2kxI+8fwesT4nLDKe9qti3ZVVZXUublFGkQm18v8bqbcaHvUq+ABxsUXpnZyANv0urEqRR5IYhKKq7Ykg8KZR0CEBDr1JWlLeVdE9nxHu9X0iugdZMdpdxh8vqUUSFvEW+Yxa7C+bUZD+xbYYFbfukFSsiLkISUO/0ZEZ/RoKDnVJedGQwNbidtX3wo25/46QQBBMxEAAJiptrwIluUnesaFztX3o+CZ4CxG5a5R/vS4thh0iD/hpNfSe7Fd59ZJ81OYnf2/ESTUhhH7K2Yn2x4XKG6prpB4vw6qKi8gNgpJYvfyYIo6TURd+S8+96u06toS8pCWn9ipjSYvSBmsOR4cHL4f2j0wfbU3f9+1ULBXm6tKpINAsQBryAAAfGKarZOId15vSM/tTjzyYP8n+9+hAYGPUe88r5nQGvq7Psn1Z2/M3mx+/Nph7tKXpLt/prOOi0OlrpDAALiDj2c61ECtQeY2dU4r5Bn9+L8NMID9J187tCl829MKNh/GK/oHhDUVtoXfHzY+7Qw5kvaiokCHm0fyMzzBCAgnmeOHHUmUF5VSrxW4nxxOrEfL57VxGtYeH8LdhDILll4nQovkFwWN1ZasT3rSA/66ujn0oA2u/b44eQcaf1EwJm1kpdiXrV9LDeUkgtjpQFwXrzHDgkrayp1Lg2SBwHzEoCAmLduYBkIgAAImJoABMTU1QPjQAAEQMC8BCAg5q0bWAYCIAACpiYAATF19cA4EAABEDAvAQiIeesGloEACICAqQlAQExdPTAOBEAABMxLAAJi3rqBZSAAAiBgagIQEFNXD4wDARAAAfMSgICYt25gGQiAAAiYmgAExNTVA+NAAARAwLwEICDmrRtYBgIgAAKmJvD/82JF259XzXIAAAAASUVORK5CYII=[/img][/td][/tr][/table]Find the scale factor.
Find the value of [math]x[/math].