[b][size=150]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[br][/size][/b][br]前回は[br]K上の多項式f(x)の分解体Lのガロア群Gで、[br]Lの中間体MとGの部分群Hの１対１対応、ガロア対応をさぐりました。[br][br][b][size=150]中間体Mに対応する部分群H=M*, [br]部分群Hに対応する中間体M=H¥[br][/size][/b][br]もちろん、[color=#0000ff][b][size=150]代数拡大L/K自体はガロア拡大なら、中間体MでもL/Mもガロア拡大だった。[br]しかし、中間体M/Kがガロア拡大であるとは限らない[/size][/b][/color]。[br][br]今回は、ガロア対応の[br][b][size=200]根っこの部分M/Kがガロア拡大になっているか[br][/size][/b]を探ってみよう。[br][br]そのために、ガロア拡大の定義の確認をしておこう。[br]（ガロア拡大と正規拡大の差異は、今のところ不問にします。[br]体としては有限次元Fpなどは除外しています。）[br][br][size=150][b]＜ガロア拡大＞[br][/b]次は、同値[br][/size][size=150]・代数拡大L/Kで自己同型群G=Aut(L/K)で[b][color=#0000ff]不変な体[/color][/b][/size][size=150][b][color=#0000ff]L[sup]G[/sup]=K[/color][/b]なら、[b][color=#0000ff]L/Kはガロア拡大[/color][/b]だ。[/size][br][size=150]・任意のｘ∈Lについて、ｘのK上の[b][color=#0000ff]共役[/color][/b]は、どれもLに属している。(正規拡大）[br]・体LはK上の多項式f(x)∈K[x]の[b][color=#0000ff]最小分解体[/color][/b]だ。[br][br][b]＜中間体がガロア拡大＞[br][/b]L/Kがガロア拡大のとき、[br]・中間体[u]からの[/u][b]拡大L/Mはガロア拡大[/b]だ。M*=Gal(L/M)はFix[sub]G[/sub](M)[br]・中間体[u]への[/u][b]拡大M/Kがガロア拡大なのは、[/b]Fix[sub]G[/sub](M)が[b]Gの正規部分群[/b]のときに限る。[br][/size]　このとき、M*=Gal(M/K)=G/[sub]FixG(M)[br][/sub][size=100][size=150]KがQの拡大体で、L/Kを[b]２次拡大[/b]とすると、L/Kはガロア拡大だ。[br][/size][/size][color=#0000ff]（理由）[/color][br][L:K]=2からKにない元a∈Lで、aのK上の最小多項式をf(x)とすると、f(x)の次元は２となる。[br]aのK上共役をa,bとすると、解と係数の関係から、b∈Lが言えるので、Lがf(x)の最小分解体。[br][br][b][size=150]＜ガロア拡大だけのガロア対応＞[br][/size][/b]ということは、[br]K上の多項式f(x)の分解体Lのガロア群Gで、[br]Lの中間体MとGの部分群Hの１対１対応、ガロア対応をさぐりました。[br]拡大の後半L/Mはガロア拡大になるので、拡大の前半M/Kがガロア拡大かどうかがわかればよい。[br][br]Gの[b]正規部分群[/b]がNだとわかれば、それに対応する中間体M=N¥がKに対して[br]M/Kがガロア拡大になるから、[b]ガロア拡大だけでできたガロア対応[/b]を作ることができる。[br][br][color=#0000ff]（例）[/color]f(x)=x[sup]3[/sup]-2の分解体Lのガロア群からガロア拡大だけでできたガロア対応を作る。[br]最小多項式の根の共役をu1,u2,u3= [math]\sqrt[3]{2}[/math] , ω [math]\sqrt[3]{2}[/math] , ω[sup]2[/sup] [math]\sqrt[3]{2}[/math] とおこう。[br]分解体L＝Q( [math]\sqrt[3]{2}[/math] ,ω)=Q({a+bω+c [math]\sqrt[3]{2}[/math] +dω [math]\sqrt[3]{2}[/math] +e [math]\sqrt[3]{2}[/math] [sup]2[/sup]+fω [math]\sqrt[3]{2}[/math] [sup]2[/sup] | a,b,c,d,e,f∈Q}＝ Q(u1,u2,u3)だ。[br]ガロア群G=Gal(L/K)={e, s:(1 2 3), ss:(1 3 2), a:(1 2) , b:(1 3) ,c :(2 3)} [b]=S3[/b][br]自明でない部分群H={A,B,C,N}={{e,a},{e,b},{e,c},{e,s,ss}}[br]対応する中間M={C¥,B¥,A¥,N¥}={Q(u1),Q(u2),Q(u3),Q(ω)}[br]中間体M={A,B,C,N}のどれでも、代数拡大M/Hはガロア拡大になるので、これは調べない。[br]・Aut(Q(u1))=Aut(Q(u2))=Aut(Q(u3))={id}だから、自己同型写像の不変体が基底のQではなく、[br]中間体自身になってしまうので、ガロア拡大ではない。[br]・しかし、Q(ω)/Qは、ωのQ上の最小多項式がf(x)=x[sup]3[/sup]-1で、f(x)の解ωの共役1,ω,ω2がQ(ω)に属するので[br]Q(ω)はf(x)の最小分解体だから、ガロア拡大だ。N={e,s,ss}がGの正規部分群という理由からも言えるね。

[b][size=150]＜正規部分群の判定＞[/size][/b][br]正規部分群にはgN＝Ng、言い換えるとN＝g[sup]−１[/sup]Ng[br]共役写像（自己同型写像）igで不変な部分群という調べ方があった。[br][br][color=#9900ff][b][u][size=150]質問：クラインの４元群V4の３つの部分群が正規部分群かどうかをコードでしらべるにはどうしましょう。[br][/size][/u][/b][/color]V4の４元e,a,b,cを平面の４象限の置換をイメージして辞書{もと:行き先}で定義します。[br]e={1:1,2:2,3:3,4:4}[br]a={1:2,2:1,3:4,4:3}[br]b={1:4,2:3,3:2,4:1}[br]c={1:3,2:4,3:1,4:2}[br]V4はS=[e,a,b,c]で、部分群は３つA=[e,a]、B=[e,b]、C=[e,c]です。[br]部分群A,B,Cそれぞれに対して、[br]igx関数で、g,xから置換辞書ｘから共役な置換辞書ｙを返します。[br]igxs関数は、群の置換ぜんぶをxsで渡して、ぜんぶ共役にしたリストを返します。[br]make_auto関数は、群Gの部分群Hを渡すと、その全部の要素の、Gの要素ｇによる共役を計算したリスト[br]nameListを計算しながら表示します。そして、もとのHの要素の集合とnameListを蓄積したリストをユニークな集合にします。最後にそれを比較して、Hが正規部分群かどうかのメッセージを出します。[br][IN]Python[br]#=============[br]def ami2dic(ami):[br] return dict(zip(ami , ami[1:] + [ami[0]]))[br]def amis2dics(amis):[br] return [dict(zip(ami , ami[1:] + [ami[0]])) for ami in amis][br]# ｋの辞書dic_aによる行先を返す。辞書にないなら行先はｋ。[br]def ami_go(k,dic_a):[br] return dic_a[k] if k in dic_a.keys() else k[br]#あみだの辞書a,bの連結をする。[br]def conL(a,b):#a,bの順に演算する。[br] keys = list(set(list(a.keys()) + list(b.keys())))[br] dic ={key:ami_go(ami_go(key,a),b) for key in keys if key !=ami_go(ami_go(key,a),b)}[br] if len(dic)==0:[br] dic={1:1}[br] return dic[br]def conR(a,b):#b,aの順に演算する。[br] return conL(b,a)[br]#アミダを、(辞書,名)のタプルのリストにする。[br]def rotdic(S,SN):[br] dic=[ami2dic(x) for x in S][br] return list(zip(dic,SN))[br]# あみだ辞書dic_aを名で返す。[br]def name(dic_a):[br] global Nlist[br] return [item[1] for item in Nlist if item[0]==dic_a][0][br]# あみだ辞書集dicsを名のリストで返す。[br]def names(dics):[br] global Nlist[br] return [item[1] for item in Nlist for b in dics if item[0]==b][br]# あみだ辞書の集合Hと辞書aを演算した結果リストを返す。[br]def Ha(H,a):[br] global Nlist[br] res=[][br] for b in H:[br] res +=[item[1] for item in Nlist if item[0]==conR(b,a)][br] return res[br]def aH(a,H):[br] global Nlist[br] res=[][br] for b in H:[br] res +=[item[1] for item in Nlist if item[0]==conR(a,b)][br] return res[br]#==================================以上が基本関数====================[br]#辞書リストS,名リストSNから（辞書、名）のタプルのリストにする。[br]def Ndic(S,SN):[br] return list(zip(S,SN))[br][b]def igx(g,x):[br] global Ssize[br] n = Ssize[br] keys=[ami_go(k,g) for k in range(1,n+1)][br] vals=[ami_go(ami_go(k,x),g) for k in range(1,n+1)][br] return dict(zip(keys,vals))[br]def igxs(g,xs):[br] return [igx(g,x) for x in xs][br][/b]#=========ここからがデータ入力[br]Ssize=4[br]e={1:1,2:2,3:3,4:4}[br]a={1:2,2:1,3:4,4:3}[br]b={1:4,2:3,3:2,4:1}[br]c={1:3,2:4,3:1,4:2}[br]S=[e,a,b,c][br]A=[e,a][br]B=[e,b][br]C=[e,c][br]SN=["e","a","b","c"][br]Nlist=Ndic(S,SN)[br]#内部自己同型の演算表を作る[br][b]def make_auto(H):[br] global Nlist[br] targetset = set(names(H))[br] goalList= [][br] G = [x[0] for x in Nlist][br] print("igの対象=",names(H))[br] for item in G:[br] nameList= names(igxs(item,H))[br] print(name(item),"→",nameList)[br] goalList.extend(nameList)[br] goalset=set(goalList)[br] print(targetset,"→",goalset)[br] msg = f"だから、{targetset}は正規部分群"[br] msg += "です。" if targetset == goalset else "ではありません。" [br] print(msg)[br] return True[br][/b]print("G∍gによる内部自己同型")[br]make_auto(A)[br]make_auto(B)[br]make_auto(C)[br][b]#===============[br][OUT][br]G∍gによる内部自己同型[br]igの対象= ['e', 'a'][br]e → ['e', 'a'][br]a → ['e', 'a'][br]b → ['e', 'a'][br]c → ['e', 'a'][br]{'e', 'a'} → {'e', 'a'}[br]だから、{'e', 'a'}は正規部分群です。[br]igの対象= ['e', 'b'][br]e → ['e', 'b'][br]a → ['e', 'b'][br]b → ['e', 'b'][br]c → ['e', 'b'][br]{'b', 'e'} → {'b', 'e'}[br]だから、{'b', 'e'}は正規部分群です。[br]igの対象= ['e', 'c'][br]e → ['e', 'c'][br]a → ['e', 'c'][br]b → ['e', 'c'][br]c → ['e', 'c'][br]{'e', 'c'} → {'e', 'c'}[br]だから、{'e', 'c'}は正規部分群です。[br][br][/b][color=#0000ff]たとえば、[br][/color]f(x)=(x[sup]2[/sup]-2)(x[sup]2[/sup]-3)の分解体Lのガロア群Gはクラインの４元群V4のガロア拡大のガロア対応を作りたい。[br][br]さっそく、V4の３つの部分群が正規部分群であることが使える。[br]分解体L=Q(√2,√3)={a+b√2+c√3+d√6 | a,b,c,d∈Q}だ。[br]ガロア群G=Gal(L/Q)=[b]V4=Z/2Z×Z/2Z[/b]={(0,0),(0,1),(1,0),(0,0)}={e,a,b,c}[br]自明でない部分群H={A,B,C}={{e,a},{e,b},{e,c}}[br]対応する中間体M={A¥,B¥,C¥}={Q(√3),Q(√2),Q(√6)}のどれでも、代数拡大L/Mはガロア拡大になる[br]対応する中間体M/Qはすべて[b]２次拡大でもあり、Hが正規分群[/b]だから、ここもガロア拡大だ。[br]ガロア対応がオールガロア拡大になったね。

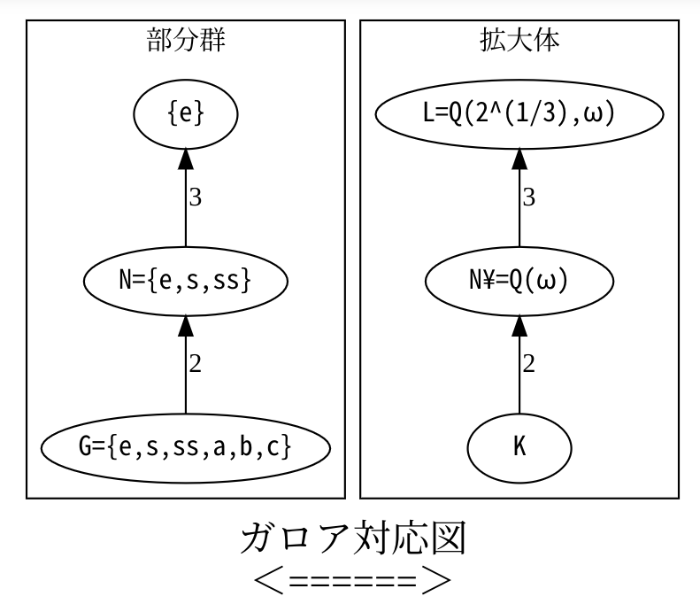
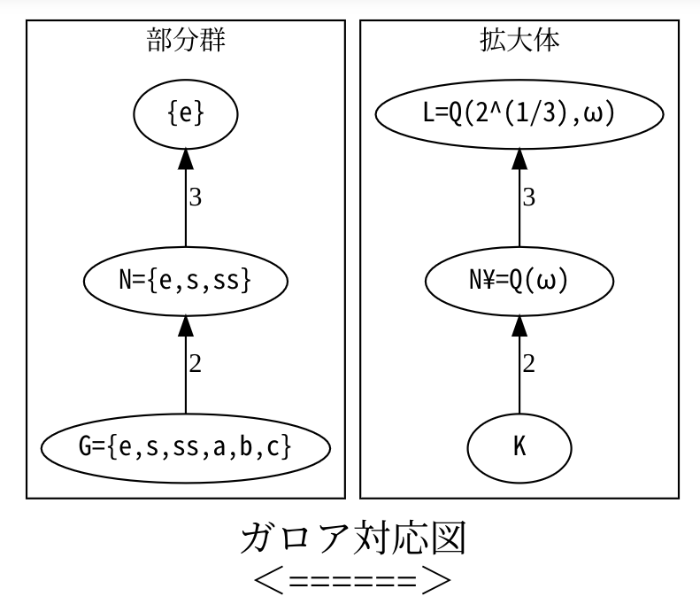
[color=#9900ff][u][b][size=150]質問：ガロア拡大だけのガロア対応を視覚化するにはどうしたらよいでしょう。[br][/size][/b][/u][/color][br]部分グラフを左右に並べて、上下関係を考えならが線を引きましょう。[br]ノードを別にかかず、エッヂをひくときにノード名をかけばよいですね。[br]部分群どうしの指数や拡大次数は計算ではなく、リストで与えると[br]見やすくなります。[br][br]#最小多項式がx^3-2の分解体Lのガロア群S3の部分群に対する、ガロア対応のガロア拡大[br]from graphviz import Digraph[br]def hasses(dot,itemG,itemK,sizeG,sizeK):[br] with dot.subgraph(name="cluster0") as G:[br] for pos in range(len(sizeG)-1):[br] a = itemG[pos][br] b = itemG[pos+1][br] G.edge(a,b,str(sizeG[pos+1]//sizeG[pos]),dir='back') #上が小、下が大（上に部分群）[br] G.attr(label='部分群')[br] with dot.subgraph(name="cluster1") as G:[br] for pos in range(len(sizeK)-1):[br] a = itemK[pos][br] b = itemK[pos+1][br] G.edge(a,b,str(sizeK[pos]//sizeK[pos+1]),dir='back') #上が大、下が小（上に拡大）[br] G.attr(label='拡大体')[br] return True[br]#=====================================================[br]dot = Digraph(format='png')[br]dot.attr('node', fontname="MS Gothic")[br]itemG=["{e}","N={e,s,ss}", "G={e,s,ss,a,b,c}"][br]itemK=["L=Q(2^(1/3),ω)","N¥=Q(ω)","K"][br]sizeG=[1,3,6][br]sizeK=[6,2,1][br]hasses(dot,itemG,itemK,sizeG,sizeK)[br]dot.attr(label=r'ガロア対応図 \n ＜======＞\n')[br]dot.attr(fontsize='20')[br]dot

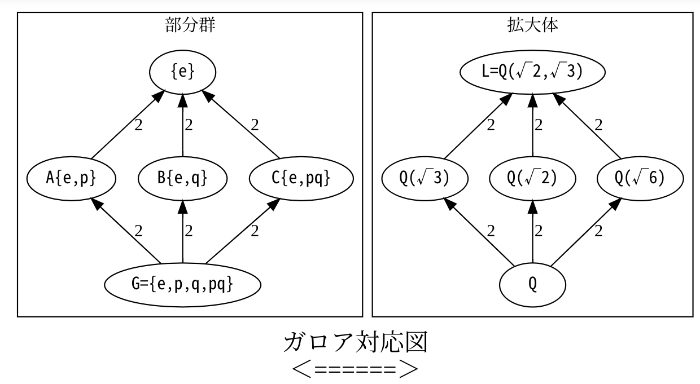
#最小多項式が(x^2-2)(x^2-3)の分解体Lのガロア群V4の部分群に対する、ガロア対応のガロア拡大[br][br]残念ながら汎用性がないので、ガロア拡大に応じて、コードも修正が必要になるね。[br][br]from graphviz import Digraph[br]def hasses(dot,itemG,itemK,sizeG,sizeK):[br] size=len(sizeG)-1[br] with dot.subgraph(name="cluster0") as G:[br] for pos in range(1,size):[br] a = itemG[0][br] b = itemG[pos][br] G.edge(a,b,str(sizeG[pos]//sizeG[0]),dir='back') [br] for pos in range(1,size):[br] a = itemG[pos][br] b = itemG[size][br] G.edge(a,b,str(sizeG[size]//sizeG[pos]),dir='back') [br] G.attr(label='部分群')[br][br] with dot.subgraph(name="cluster1") as G:[br] for pos in range(1,size):[br] a = itemK[0][br] b = itemK[pos][br] G.edge(a,b,str(sizeK[pos]//sizeK[0]),dir='back') [br] for pos in range(1,size):[br] a = itemK[pos][br] b = itemK[size][br] G.edge(a,b,str(sizeK[size]//sizeK[pos]),dir='back') [br] G.attr(label='拡大体')[br][br] return True[br]#=====================================================[br]dot = Digraph(format='png')[br]dot.attr('node', fontname="MS Gothic")[br]itemG={0:"{e}",1:"A{e,p}",2:"B{e,q}",3:"C{e,pq}",4:"G={e,p,q,pq}"}[br]itemK={0:"L=Q(√2,√3)",1:"Q(√3)",2:"Q(√2)",3:"Q(√6)",4:"Q"}[br]sizeG=[1,2,2,2,4][br]sizeK=sizeG[br]hasses(dot,itemG,itemK,sizeG,sizeK)[br]dot.attr(label=r'ガロア対応図 \n ＜======＞\n')[br]dot.attr(fontsize='20')[br]dot[br]