[size=150]Calculus integration involves various types of integrals, each with its own set of rules and techniques. Here are some common types of integrals with examples:[br][br]1. Power Rule:[br]The power rule is used to integrate functions of the form f(x) = x^n, where n is any real number except -1.[br][br] Example: ∫(3x^2) dx = x^3 + C[br][br]2. Constant Rule:[br]The constant rule states that the integral of a constant multiplied by a function is equal to the constant multiplied by the integral of the function.[br][br] Example: ∫(5sin(x)) dx = -5cos(x) + C[br][br]3. Trigonometric Integrals:[br]Trigonometric integrals involve integrating functions containing trigonometric functions.[br][br] Example: ∫(cos(x)) dx = sin(x) + C[br][br]4. Exponential and Logarithmic Integrals:[br]Exponential and logarithmic integrals involve functions containing exponential and logarithmic functions.[br][br] Example: ∫(e^x) dx = e^x + C[br][br]5. Integration by Substitution:[br]Substitution involves substituting a variable or expression with a new variable to simplify the integral.[br][br] Example: ∫(2x+1)^3 dx (Let u = 2x+1) = ∫u^3 (1/2) du = (1/2) * (u^4/4) + C = (1/8) * (2x+1)^4 + C[br][br]6. Integration by Parts:[br]Integration by parts is used to integrate the product of two functions.[br][br] Example: ∫x * sin(x) dx = -x * cos(x) + ∫cos(x) dx = -x * cos(x) + sin(x) + C[br][br]7. Trigonometric Substitution:[br]Trigonometric substitution is a technique used to simplify integrals involving radical expressions using trigonometric identities.[br][br] Example: ∫sqrt(1-x^2) dx (Let x = sin(u)) = ∫cos^2(u) du = ∫(1+cos(2u))/2 du = (u/2) + (sin(2u))/4 + C[br][br]8. Partial Fractions:[br]Partial fractions are used to decompose a rational function into simpler fractions to make integration easier.[br][br] Example: ∫(3x+1)/(x^2+2x+1) dx = ∫(3x+1)/(x+1)^2 dx = ∫(A/(x+1) + B/(x+1)^2) dx[br][br]These are just a few examples of the different types of integrals and techniques used in calculus integration. Each type requires specific strategies and methods to evaluate the integral, and the choice of technique depends on the form of the function being integrated.[/size]

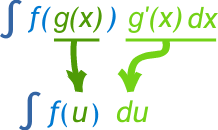
Integration by substitution is one of the basic methods of integration. An integral of the type [br][math]\int g'\left(x\right)f\left(g\left(x\right)\right)dx[/math][br]is an example where this method may be applicable. Sometimes using substitution [math]t=g\left(x\right)[/math] may convert the integral to a form suitable for another method. Purpose of this applet is to facilitate practice of the method of integration by substitution.

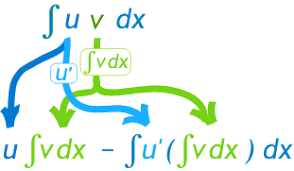
Integration by parts is one of the basic methods of integration. Integration by parts, integration by substitution, and their combination provide powerful techniques of integration. Integration by parts is applicable when the integrand is a product of two functions, at least one of which is integrable and the other differentiable. There are some exceptions, for example if the integrand is [math]ln\left(x\right)[/math], it may be written as product of two functions by writing [math]ln\left(x\right)=1\times ln\left(x\right)[/math]. Similar comment applies to inverse trig functions too. Integration by parts may have to be applied more than once in some cases, for example, when an integrand is of the form [math]x^3e^x,x^2sin\left(x\right),e^xsin\left(x\right)[/math] etc. Purpose of this applet is to facilitate practice on method of integration by parts. Follow the instructions that may be viewed by checking the Instructions check box.

The purpose of this applet is to facilitate practice in finding partial fraction decomposition of a rational function, [math]\frac{f\left(x\right)}{g\left(x\right)}[/math], where degree of [math]f\left(x\right)[/math] is less than that of [math]g\left(x\right)[/math] . First, the denominator [math]g\left(x\right)[/math] is completely factored. For example, if [math]g\left(x\right)=\left(x-a\right)\left(x-b\right)\left(x-c\right)^2\left(x^2+u\right)\left(x^2+v\right)^2[/math] partial fraction decomposition of [math]\frac{f\left(x\right)}{g\left(x\right)}[/math]is of the form[br][math]\frac{f\left(x\right)}{g\left(x\right)}=\frac{A}{x-a}+\frac{B}{x-b}+\frac{C}{\left(x-c\right)}+\frac{D}{\left(x-c\right)^2}+\frac{Ex+F}{x^2+u}+\frac{Gx+H}{x^2+v}+\frac{Jx+K}{\left(x^2+v\right)^2}[/math][br]The above factorization of [math]g\left(x\right)[/math] is used to create a template of decomposition. The questions in this applet are much simpler.[br]Follow the instructions to use the applet.