[b][size=150]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[br][/size][/b][br][b][size=150]＜環のリングのゴングはなった！＞[br][/size][/b]きちんとルールに合格した体（フィールド）とちがって、環（リング）は少しずっこけていても参加できる場所だった。ということは、環のリングには、普通でない？数も参加できるという気がするね。[br][br]では、どんな数が登場できるのだろうか？

[b][size=150]＜ガウス整数は環だ＞[br][/size][/b]ガウス整数は複素数で実部も虚部も整数のものだ。[br]いたって単純な定義だ。これが環なら[b][color=#0000ff]ガウス整数環[/color][/b]と名付けてあげよう。[br]整数の集まりをZ[i]とかこう。[br]２項演算＋について、[u]＜Z[i]、＋＞は可換群[/u]だ。[br]・閉性。a,b∈Zならa+b∈Z[i] 。[br]・ゼロは０+0i∈Z[i]だ。[br]・＋算は結合法則が成り立つ。[br]・ｘ+yi∈Zの反元は１つのだけ -ｘ+(-y)i∈Z[i]がある。[br]（＋算は交換法則が成り立つ。成分ごとに見ると整数和だからOK。）[br][br]２項演算×について、[u]＜Z[i]、×＞は可換なモノイド[/u]だね。[br]・閉性。x=a+bi, y=c+di∈Z[i]ならxy=(ac-bd)+(ad+bc)i∈Z[i]でOKだ。[br]・イチは1+0i∈Z[i]だ。[br]・×算は結合法則が成り立つ。[br]（×算は交換法則が成り立つ。成分ごとに見ても交換できるからOK）[br]（[color=#0000ff]逆元がある元（単元）[/color][b]は±１，±iの４元あるね。）[br][/b][br]＋、×についての分配法則が成り立つ。[br]a,b,c∈Z[i]なら(a+b)×c=a×c+b×c[br][br][b][size=150]＜複素数のノルム＞[br][/size]複素数xの原点からの距離の２乗をノルムといい。[br][/b]ノルムはN(x)とか、|x|[sup]2[/sup]などとかく。[br]N(x)は非負であり、N(x)=0となるのは、x=0に限る。[br][b][color=#0000ff]N(ab)=N(a)N(b)[/color][/b]。だから、Nは準同型写像でもある。[br]単元のノルム＝１とすると、x[sup]2[/sup]+y[sup]2[/sup]=1となるのは実部か虚部の片方だけの絶対値＝１だから、[br][b]単元は±１，±iとなるね。[br][/b]ガウス整数aの単元倍をした数を[b]同伴数[/b]という。a,-a,ai,-aiが互いに同伴数になる。[br]

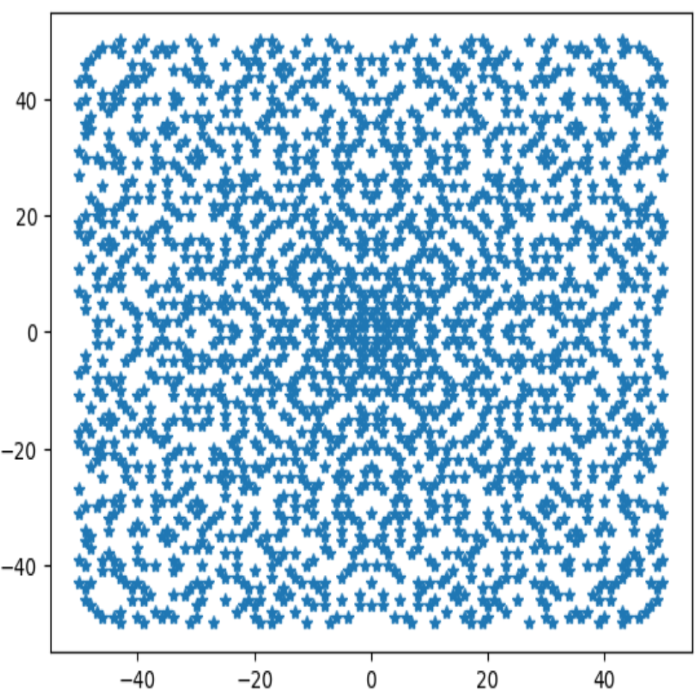
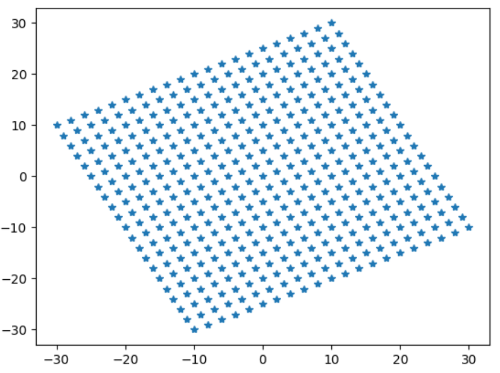
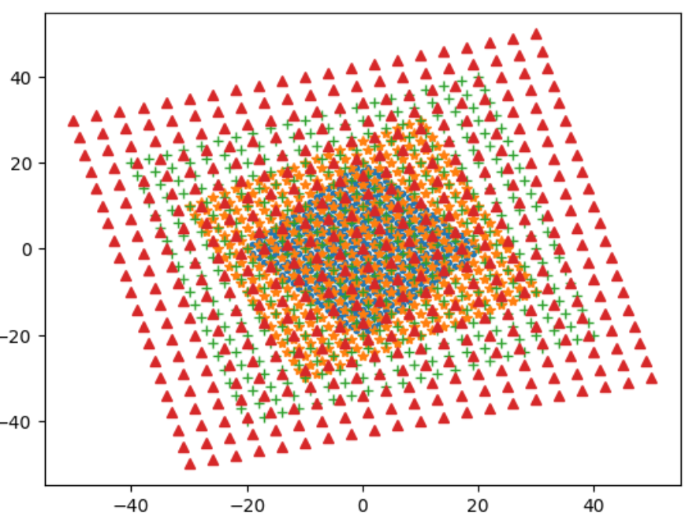
[b][size=150]＜ガウス整数の倍元＞[/size][/b][br]ガウス整数x=a+biの倍元どうしはどんな関係になるだろうか。[br]ｘに任意のガウス整数y=m+niをかけたものxy=x(m+ni)=m(x)+n(ix)となる。[br]だから、x=a+biとix=i(a+bi)の一次結合といえるね。iはｘを90度回転する働きがある。[br]だから、ガウス平面をベクトル平面としてみると、[br][b][color=#0000ff]ベクトルx=(a,b)を90度回転したix=(-b,a)と原点が作る正方形の４頂点を平行移動した格子点[/color][/b]が[br]ｘ＝a+biの倍数となるね。[br][br][color=#9900ff][b][size=150][u]質問：ガウス整数1+i,2+i,3+i,4+i,の倍元を視覚化するにはどうしたよいでしょうか。[br][br][/u][/size][/b][/color]まず、m=2 + i とします。pythonでは、虚数単位をjとして、虚部が１のときは1jとかきます。[br]また、mにｘ+yi をかけるとき、x,yを-10以上10以下に動かしたいので、[br]複素数の生成関数で[b]complex(x,y)[/b]のようにして、20*20=400個の倍元集合を作ります。[br]点ごとドットができないので、ｘ座標の数列とｙ座標の数列をリスト渡して描画しましょう。[br]うまく動くのを確認したら、[br]#=============== １つで実験[br][IN]python[br]import numpy as np[br]import matplotlib.pyplot as plt[br]m = 2 + 1j[br]fig = '*'[br][b]bai=[m*complex(x,y) for x in range(-10,10) for y in range(-10,10)][br]xs=[c.real for c in bai][br]ys=[c.imag for c in bai][br]plt.plot(xs,ys,fig)[br][/b]#========================　複数を同時にかく[br][IN]python[br]import numpy as np[br]import matplotlib.pyplot as plt[br]m = [1 + 1j, 2 + 1j, 3 + 1j, 4 + 1j][br]fig = ['.','*','+','^'][br]for num in range(len(m)):[br] bai=[m[num]*complex(x,y) for x in range(-10,11) for y in range(-10,11)][br] xs=[c.real for c in bai][br] ys=[c.imag for c in bai][br] plt.plot(xs,ys,fig[num])[br][br][OUT][br][br]geogebraでも視覚化してみよう。[br]

[b][size=150]＜割り算の商と余り＞[/size][/b][br]ガウス整数x=a+biの高さH(x)をノルムN(x)=a[sup]2[/sup]+b[sup]2[/sup]で定義してみよう。N(x)は非負整数だ。[br]・H(x)=0の核はx=0に限るから、１対１対応でOK。[br]・非ゼロのx,y∈Z[i]でH(xy)>=H(x)。＝はyが単元のときに限るからOK。[br]・どの非ゼロのx、y∈Z[i]に対しても、[br]　q,r∈Z[i]があり、y=qx+r で、0<=H(r)＜H(x)となる最小のｒがあるか？[br]　両辺をxで割ると、y/x= q + r/x, H(r/x)<1 [br] z= y/x＝a+bi（a,b∈R)。[br]　zがガウス平面の格子点のとき、つまり、ｚ∈Z[i]なら、H(r/x)<1だから、r=0。[br]　zが格子点でなく、近い格子点の１つがｃならH(z-c)<1。商をcとするときの余りをrとすると、[br]　z=y/x, xz=yから、r=y-cx=xz-cx=x(z-c)だから、N(r)=N(x)N(z-c)＜N(x)[br] 商も余りも求められるが、格子点でないときは１通りとは限らない。[br]・割る数よりも小さな余りがあるということは、ガウス整数はユークリッド互除法が使える整域、[br]　ユークリッド整域だね。[br]　ユークリッドの互除法が、ガウス整数での使えるから、[br]　最大公約元が見つかり、素因子分解もできるはずだね。[br]（例）[br] y=5+0i, x=-3+0iなら、y/x=5/-3 , [br] 5=(-1)×(-3)+2 商が-1で、余りが2。[br]　5=(-2)×(-3)+(-1)　商が-2で、余りが-1。[br]　どちらの余りもノルムはN(-3）より小さいが、[b]最小のノルムは(-1)のとき[/b]だから、[br]　y÷xの商は-2で、余りは-1となるね。[br]（例）[br]　y=5+4i, x=2-i なら、y/x=y*1/x=y*x'/N(x)=(5+4i)*(2+i)/5=(5*2-4*1)/5+(5*1+4*2)/5i=1.2+2.6i [br]　y/xに近い格子点はq=1+3i。r=y-qx=5+4i-(1+3i)(2-i)=5+4i-{(1*2+3*1)+(6-1)i)=5+4i-5-5i=-i[br] N(x)=5, N(r)=1だから、rは余りとなる。y÷xの商は1+3i, 余りは-i[br][br][color=#9900ff][b][u][size=150]質問：ガウス整数でのA÷Bの整除によりQとRを求めるコードでかくとどうなりますか。[br][/size][/u][/b][/color][br]A/Bに近い格子点は、ガウス平面でA/Bを囲む正方形の４つの頂点の複素数になります。[br]それぞれの格子点はcomplex(p,q)のようにして複素数を書き出し、４点のリストを作ろう。[br]格子点とA/Bとの距離のリストを作り、最小になるインデックスをargminというnumpyの関数を[br]使って取り出します。こうすると最も近い格子点が取り出せます。[br]この格子点が商Qになります。余りR=A-B*Qで求められるね。[br][b]複素数cのNorm関数はなく、abs(c)を使います。absを２乗しないとノルムにならないのですが、[br]大小比較だけなら、絶対値で十分ですから。[br]pythonとgeogebraでやってみよう。[br][/b][br][IN]Python[br]#ガウス整数の割り算[br]import numpy as np[br]def divg(A, B):[br] h=abs(B)[br] if abs(B)<2:[br] print("割る数は単元以外にしてください。")[br] return A,B,[],[][br] qC = A/B[br] print(f"A/B={qC}")[br] [b][color=#0000ff] rel = qC.real[br] img = qC.imag[br] xl, yB = int(rel),int(img)[br] xr, yT = xl + 1, yB + 1[br] grid = [complex(xl,yT),complex(xl,yB),complex(xr,yT),complex(xr,yB)][br] dists = np.array([abs(k-qC) for k in grid])[br] print(f"{grid}=> {dists}")[br] indx = dists.argmin()[br] Q = grid[indx][br][/color][/b] R = A - B * Q[br] return A,B,Q,R[br][br]y = 5 + 4j[br]x = 2 -1j[br]A,B,Q,R = divg(y,x)[br]print(f"{A}＝{B}×{Q} + {R}")[br]print()[br][b][color=#0000ff][OUT][br]A/B=(1.2+2.6j)[br][(1+3j), (1+2j), (2+3j), (2+2j)]=> [0.4472136 0.63245553 0.89442719 1. ][br](5+4j)＝(2-1j)×(1+3j) + -1j[br][/color][/b][br][br][b][size=150]＜ガウスの素元＞[/size][/b][br]3+4iは素元か？[br]3+4i=abとすると、N(3+4i)=N(a)N(b)[br]N(3+4i)=25だから、a,bが単元でないなら、N(a)=N(b)=5=4+1=(±2)[sup]2[/sup]+(±i)[sup]2[/sup]=(±1)[sup]2[/sup]+(±2i)[sup]2[/sup][br]このうち、3+4i=(2[sup]2[/sup]-1)+2*2i=(2+i)[sup]2[/sup][br]3+4iは素元ではない。[br][br]2=1[sup]2[/sup]-i[sup]2[/sup]=(1+i)(1-i)となるから、２は素元でなない。[br]5=4+1=2[sup]2[/sup]-i[sup]2[/sup]=(2+i)(2-i)となるから、５は素元でないね。[br]3,7,11,19,23は素元だ。[br]13=9+4=3[sup]2[/sup]-(2i)[sup]2[/sup]=(3+2i)(3-2i)となるから、１３は素元でない。[br]17=16+1=(4+i)(4-i)となるから、１７は素元でない。[br]29=25+4=(5+2i)(5-2i)となるから、２９は素元でない。[br]素元でないのは２か、5,13,17,29のように1(mod 4)だと気づく。[br]素元は3,7,11,19,23のように-1(mod4)と気づくね。[br]どうしてそうなるのだろうか？[br][br][b][size=150]＜素数pがガウスの素元になるとき＞[br][/size][/b]整数のときのように、単元でも素元でもない元を合成元と呼んでみよう。[br]ｐが素数でも、ガウス整数としては合成元となりうるね。[br]だから、非単元のa,bを使ってp=abと分解できる。[br]素数ｐには虚部がないので、形式的にpの2乗をpとｐの共役元の積とみなすこともできる。[br]p[sup]2[/sup]=pp'=ab(ab)'=aa' bb'=N(a)N(b)となる。[br]だから、p=N(a)=N(b)に限るね。a=m+niとおくとN(a)=m[sup]2[/sup]+n[sup]2[/sup]だから、[br]素数ｐが平方数の和になる。[br]m,nともに偶数ならp=N(a)≡0+0=0(mod 4)となり、素数pが４の倍数になることになり、あり得ない。[br]mが偶数、nが奇数ならp=N(a)≡0+1=1(mod 4)となる。[br]m,nともに奇数ならp≡1+1=2(mod 4)となる。ｐが素数だから、p=2のみあり得る。[br]だから、[color=#0000ff]素数pがガウス合成元ならｐは２か1(mod 4)[/color][b]となる。[br]この対偶は、[br][/b][color=#0000ff]２より大きい素数pが３(mod 4)ならば素数pはガウス素元になる[/color][b]。[br][/b]ではガウス素元にならなかったｐは使い道がないのだろうか？[br]そうではない。[br][b][br][size=150]＜一般のガウス素元＞[br][/size][/b]素数ｐが1(mod 4)のときは素数ｐはガウス素元のaa'の積に分解できた。[br]a=m+niとおくと、p=N(a)=m[sup]2[/sup]+n[sup]2[/sup]だから、ｐが平方数の和になり、[br]p=(m+ni)(m-ni)と分解できたね。[br]a,a'はガウス素元で、そのノルムN(a)=pが1(mod 4）の素数になっていた。[br]これを逆手にとろう。[br][b][color=#0000ff]一般に、m,n≠0のガウス整数a=m+niが素元なら、ノルムN(a)が素数になる。[br]だから、ノルムN(a)が合成数ならば、aは素元分解できる。[br][/color][/b]

[color=#9900ff][b][size=150][u]質問：素数ｐでガウス素元になるものを抜き出すにはどうしたらよいでしょう。[br][/u][/size][/b][/color][br]たとえば、1000以下の素数でガウス素元でもある数を抜き出します。[br]そのために、素数pのリストPを作ります。[br][b][color=#0000ff][size=150]filter(x-> f(x), List)[br][/size][/color][/b]これがjuliaで、リストListの要素ｘに対して、f(x)が成り立つものに制限する構文です。[br][b][color=#0000ff][size=150]a:b[br][/size][/color][/b]これがjuliaで、整数aからbまでのリストを作る構文です。[br][br]ｎを2以上1000とします。[br]ｎを１つ選んだとして、ｍが1以上n以下のリストを、n%m==0、つまりｎの約数にしたリストにします。[br]ｎに対して、リストの長さ、つまりｎの約数の個数==2になるｎ、つまり素数ｎにしたリストPにします。[br][br][b]juliaなら、高階関数が楽にかけるので、juliaを選びました。[br]見かけが少し変わりますが、他の言語でも同様にかけるでしょう。[br][/b]リストPの要素xに対して、x%4==3となるものにしたリストがガウス素元リストppです。[br][br][IN]julia[br][b][color=#0000ff]# Pは素数リスト[br]P =filter(n->length(filter( m -> n % m==0,1:n))==2, 2:1000)　[br]# ppは素数で、ガウス素元[br]pp = filter(k -> k % 4 == 3, P)[br][/color][/b]println(pp)[br][OUT][br][3, 7, 11, 19, 23, 31, 43, 47, 59, 67, 71, 79, 83, 103, 107, 127, 131, 139, 151, 163, 167, 179, 191, 199, 211, 223, 227, 239, 251, 263, 271, 283, 307, 311, 331, 347, 359, 367, 379, 383, 419, 431, 439, 443, 463, 467, 479, 487, 491, 499, 503, 523, 547, 563, 571, 587, 599, 607, 619, 631, 643, 647, 659, 683, 691, 719, 727, 739, 743, 751, 787, 811, 823, 827, 839, 859, 863, 883, 887, 907, 911, 919, 947, 967, 971, 983, 991][br][br]geogebraでも同様にかけます。[br][color=#0000ff][size=150]フィルターがfilter(x-> f(x), List)[/size][/color]ではなく、[size=150][color=#0000ff]KeepIf(f(k),k,List)[br]剰余の条件がa%b==0[/color][size=100]ではなく、[/size][color=#0000ff]Mod(a,b)==0[br][/color][color=#0000ff]整数リストが1:b[/color][size=100]ではなく、[/size][color=#0000ff]Sequence(b)[br][/color][b][br]になるので、置き換えましょう。[br][/b][/size][br]数式を表示して、１行ずつ入力してエンターします。[br]#==================[br]L=Sequence(1000)[br][size=150]P=KeepIf(Length(KeepIf(Mod(k,n)==0,n,Sequence(k)))==2,k,L)[br][/size]pp=KeepIf(Mod(k,4)==3,k,P)

[color=#9900ff][u][b][size=150]質問：ガウス整数の互除法はどうコードにできますか。[br][/size][/b][/u][/color][br][size=100]A,Bから[size=150]X=A,Y=Bとし、[/size][もし、Y＞０ならQ=X/Y, R=X-Y*Q、[size=150]X=Y,Y=R[/size] ]を繰り返すと、[br]最後の直前のYつまり、Xが最大公約数になるというアルゴリズムが互除法でした。[br]Y＞０はabs(Y)＞０とかける。Q,Rは上で作ったdivg関数を調整して使いましょう。[br][br]#ガウス整数の整除[br]import numpy as np[br]def divg(A, B):[br] h=abs(B)[br] qC = A/B[br] print(f"A/B = {A}/{B} = {qC}")[br] rel = qC.real[br] img = qC.imag[br] xl, yB = int(rel),int(img)[br] xr, yT = xl + 1, yB + 1[br] grid = [complex(xl,yT),complex(xl,yB),complex(xr,yT),complex(xr,yB)][br] dists = np.array([abs(k-qC) for k in grid])[br] indx = dists.argmin()[br] Q = grid[indx][br] R = A - B * Q[br] print(f"{A} = {B}×{Q} + {R}")[br] return A,B,Q,R[br][br][/size]#ユークリッドの互除法（ガウス整数版）[br]def eucg(A,B):[br] (X,Y) = (B,A) if abs(A)0:[br] A,B,Q,R=divg(X,Y)[br] X=Y[br] Y=R[br] return X[br]y = 23 + 16j[br]x = 13 -9j[br]print(f"G={eucg(y,x)}")[br][br][OUT][br]A/B = (23+16j)/(13-9j) = (0.62+1.6600000000000001j)[br](23+16j) = (13-9j)×(1+2j) + (-8-1j)[br]A/B = (13-9j)/(-8-1j) = (-1.4615384615384615+1.3076923076923077j)[br](13-9j) = (-8-1j)×(-1+1j) + (4-2j)[br]A/B = (-8-1j)/(4-2j) = (-1.5-1j)[br](-8-1j) = (4-2j)×(-1-1j) + (-2+1j)[br]A/B = (4-2j)/(-2+1j) = (-2-0j)[br](4-2j) = (-2+1j)×(-2+0j) + 0j[br]G=(-2+1j)

[b][size=150]＜ガウス整数ｍ＋iの素元分解＞[br][/size][/b]ノルムがN(ab)=N(a)N(b)と分解できることと、[br]ガウス整数のノルムが素数になることを利用して素元分解にチャレンジしよう。[br]ｘ＝ｍ＋i　型のガウス整数の素元分解をするには、[br]まず、ノルムN(x)が素数かどうかを計算します。素数でないなら、素因数分解し、[br]各素数に対応するガウス整数をリストアップしましょう。[br]そして、その積がｘに等しくなるものをさがします。[br]また、a+biが素元なら,単元倍の-a-bi,ai-b,b-aiも素元。[br][br]実験しやすくするために、[br]geogebraで、２要素または３要素のガウス整数の積を計算するアプリを作っておきましょう。[br][br][color=#0000ff]（例）[/color][br]N(1+i)=2から、1+iは素元[br]N(2+i)=5から、2+iは素元[br]N(4+i)=17から、4+iは素元[br]N(6+i)=37から、6+iは素元[br]N(10+i)=101から、10+iは素元[br]N(14+i)=197から、14+iは素元[br]N(16+i)=257から、16+iは素元[br][br]N(3+i)=10=2*5=N(1+i)N(2-i)より、 (1+i)(2-i)=3+i[br]N(5+i)=26=2*13=N(1+i)N(3-2i)より、(1+i)(3-2i)=5+i[br]N(7+i)=50=2*5*5と、7+i=(1+i)(4-3i)、(4-3i)/(2+i)=1-2iより7+i=(1+i)(2+i)(1-2i)[br]N(8+i)=65=5*13=N(2-i)N(3+2i) から、(2-i)(3+2i)=8+i[br]N(9+i)=82=2*41=N(1+i)N(5-4i)から、(1+i)(5-4i)=9+i[br]N(11+i)=122=2*61=N(1+i)N(6-5i)から、(1+i)(6-5i)=11+i[br]N(13+i)=170=2*85=2*5*17と、13+i=(1+i)(7-6i)、(7-6i)/(2-i)=4-iから、13+i=(1+i)(2-i)(4-i)[br]N(15+i)=226=2*113=N(1+i)N(8-7i)から、(1+i)(8-7i)=15+i[br]一般にmが奇数のとき、m=2n+1とすると、[br][b][size=150]N((2n+1)+i)=4n[sup]2[/sup]+4n+2=2(2n[sup]2[/sup]+n+1)=N(1+i)N(n+1-n i) となり、[br](2n+1) + i =(1+i)(n+1-n i)と分解できる。[br][/size][/b]　さらに、N(n+1-ni)が合成数なら、さらに(n+1-ni)が素元分解できる。[br]

[color=#9900ff][b][u][size=150]質問：実部と虚部の絶対値が５以下の範囲の素元だけを表示するコードはどうしたら作れますか。[br][/size][/u][/b][/color][br][b]ガウス素元は２種類あります。x=m+niとするとき[br]A型・N(x)=m[sup]2[/sup]+n[sup]2[/sup]が素数になるもの[br]B型・素数p≡3(mod4)を単数倍したもの[br][/b]です。B型のノルムは、p[sup]2[/sup]ですから素数ではありませんが、ガウス素元です。[br]割り算をするときにNormの代わりにabsを使いました。[br]しかし、absはルート計算までやってくれているので、Normとしては不適当です。[br]そのまま、c.real**2+c.imag**2が素数リストPの中にあるかを調べましょう。[br][br]#素元だけを表示する。[br]import numpy as np[br]import matplotlib.pyplot as plt[br]def show(length):[br] # pは素数リスト[br] norm=length**2[br] M=list(range(2,norm*2)) [br] divCount=lambda n:len(list(filter(lambda m:n % m==0, list(range(1,n+1)))))[br] P= [x for x in M if divCount(x)==2] [br] # 純虚数でも実数でもないガウス整数のnormが素数なら素元である[br] under5=[complex(x,y) for x in range(-length,length+1) for y in range(-length,length+1)][br] sogen= [c for c in under5 if c.real**2+c.imag**2 in P][br] # 純虚数か実数の素元（数の絶対値が４で割って３余る素数ｐの単元倍）[br] pp = [x for x in P if x % 4 ==3 and x < length][br] Onenum = [1,-1, 1j, -1j][br] psogen = [ x*y for x in pp for y in Onenum][br] sogen +=psogen [br] xs=[c.real for c in sogen][br] ys=[c.imag for c in sogen][br] plt.plot(xs,ys,'*')[br]show(5)

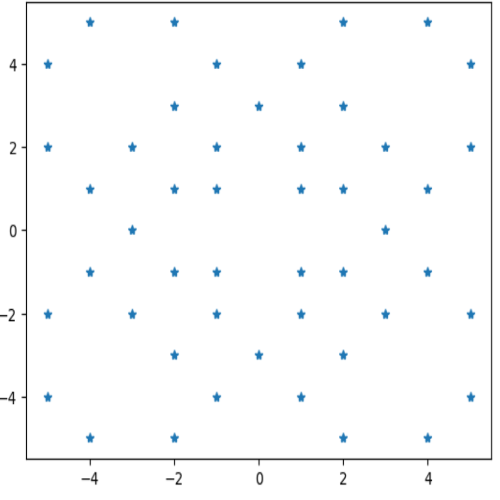
範囲を拡大して調べましょう。[br]show(50)[br][br]geogebraにコードを移し替えてみよう。