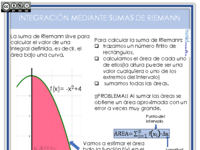
1. ¿Qué es una suma de Riemann y cómo se utiliza para aproximar el área bajo una curva? (contesta máximo en dos líneas)

2. Utilizando el applet de GeoGebra, observa los rectángulos cuando se considera la altura de cada rectángulo con el extremo izquierdo de cada subintervalo debajo de la función f(x)= [math]x^2[/math] en el intervalo [0,2]. ¿Qué observas?(contesta máximo en dos líneas)

3. Utilizando el applet de GeoGebra, observa los rectángulos cuando se considera la altura de cada rectángulo con el extremo derecho de cada subintervalo debajo de la función f(x)= [math]x^2[/math] en el intervalo [0,2]. ¿Qué observas?(contesta máximo en dos líneas)

4. Explica la diferencia entre las sumas de Riemann izquierda y derecha. Utiliza el applet para mostrar ejemplos con la función f(x)=[math]x^2[/math] (contesta máximo en dos líneas)

5. Explica por qué la suma de Riemann es una herramienta importante en el cálculo integral. Utiliza ejemplos y simulaciones del applet de GeoGebra para apoyar tu explicación.