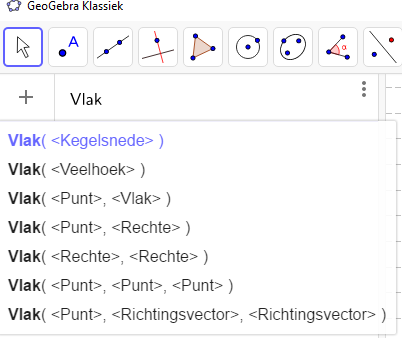
Bepaal het vlak door de punten [b][i](-1, 2, 0)[/i] en [i](1, 3, -2)[/i][/b] en // met de rechte [math]a\leftrightarrow\frac{x-1}{3}=y=\frac{z+1}{2}[/math][br]Typ [b][i]Vlak[/i][/b] in het invoerveld en bekijk de mogelijke syntaxopties:[br]De syntax van de opgave is niet rechtstreeks voorhanden, maar we kunnen wel de laatste syntax toepassen:[br][list][*]Als punt neem je een van beide gegeven punten.[/*][*]Uit de coördinaten van de gegeven punten kan je een eerste richtingscoëfficiënt afleiden.[/*][*]In de vergelijking van de evenwijdige kan je een tweede richtingscoëfficiënt aflezen.[/*][/list]

[u]Tip[/u]: De carthesische vergelijking van de rechte met twee gelijkheidstekens erin kan je zo rechtstreeks in het invoerveld typen om de rechte te creëren. Je hoeft dus niet meer de omweg via twee vlakken te maken.

Intern worden GeoGebra rechten en vlakken soms anders bepaald dan het commando dat je ingaf.[br]Rechte: Ook al typ je de vergelijking ineens, de rechte wordt bepaald als de snijlijn van twee vlakken.[br]Vlak: Je defineert het vlak als een vlak door een punt met twee gegeven richtingsvectoren, maar GeoGebra berekent dit resultaat intern als een loodvlak op het vectorieel product van deze richtingsvectoren door het gegeven punt A.